|
Préparation à l’ECE : Propriétés isolantes du plumage des canards :
1.
Mode de transfert
thermique entre l’intérieur de la boîte et le milieu extérieur.
-
Le transfert
thermique entre l’intérieur de la boîte et le milieu extérieur se fait
par convection.
2.
Les différentes
courbes.
-
Graphique :
Fichier Excel :
-
Comme le plumage de
canard possède des propriétés isolantes, le refroidissement est
plus
lent lorsque la cloison est remplie de plumes de canards.
-
La courbe
correspondant à la cloison remplie de plumes de canard se situe
au-dessus
de celle dont la cloison est sans plume.
-
La
courbe de couleur bleue correspond à la cloison sans plume.
-
La
courbe de
couleur rouge correspond à la
cloison garnie de plumes de canards.
3.
Solution de cette
équation différentielle en fonction de t et des constantes τ,
θi et θe.
-
Le système {boîte
et cloison} est assimilé à un système incompressible.
-
Il n’échange pas de
travail W avec le milieu extérieur.
-
Il échange
seulement de l’énergie Q par
transfert thermique convectif avec le
thermostat (milieu extérieur).
-
Entre l’état
initial (i) et l’état final (f),
on peut écrire :
-
ΔUi→f = Q
-
Pour une durée
suffisamment courte, on peut écrire :
-
Q = Φ . Δt
-
D’après la loi de
Newton :
-
Φ =
h .
S . (θe –
θ)
-
Q =
h .
S . (θe –
θ) .
Δt
-
D’autre part, pour
un système incompressible de masse m, de capacité thermique
massique c dont la variation de température est Δθ :
-
Q =
m .
c . Δθ
-
On obtient la
relation suivante :
-
ΔUi→f = h . S .
(θe – θ) . Δt = m . c .
Δθ
-
On peut exprimer le
rapport de l’écart de température Δθ
sur la durée Δt :
-
►
Établissement de
l’équation différentielle :
-
Lorsque
Δt → 0,
-
La limite de
l’expression
 est égale à la
dérivée de θ par rapport au temps t :
-
On écrit en
utilisant la notation différentielle :
-
:
-
En développant, on
obtient :
-
-
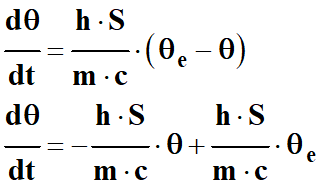
Et enfin :
-
-
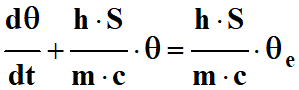
On est en présence
d’une équation différentielle linéaire du premier ordre en
θ
à coefficients constants
avec un deuxième membre constant.
-
On pose :
-
-
L’écriture de
l’équation différentielle devient :
-
-
L’équation
différentielle vérifiée par la température
θ :
- 
-
La grandeur
τ est le temps
caractéristique du système.
-
Elle admet une
solution du type :
-
-
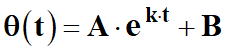
A,
B et
k sont des constantes liées aux conditions initiales et
aux
caractéristiques du système.
►
Recherche des
constantes :
-
La solution
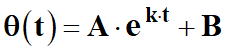vérifie
l’équation différentielle
-
Détermination de :
-
-
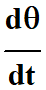
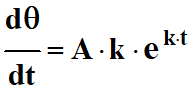
On remplace
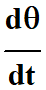et
θ par leur expression
respective dans l’équation différentielle :
-
-
La relation (2) est
vérifiée à chaque instant :
-
La grandeur
 est une constante,
-
Il faut
nécessairement que :
-
-
D’autre part, au
temps t = 0 s, θ =
θ i
-
Comme
-
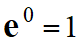
θ
i =
A + B
-
A =
θ i –
B
-
A =
θ i –
θe
-
La solution :
-
4.
Exploitation du
graphique :
-
Le temps
caractéristique τ est déterminé en traçant la tangente à l’origine sur
la courbe
θ = f (t). Lire graphiquement
τ
dans les deux expériences.
►
Détermination
expérimentale de la constante de temps τ.
-
Dans le cas
présent : θi = 8,0 ° C et θe = 40 °
C
-
Expression de :
-
-
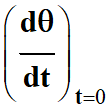
Pour déterminer
graphiquement le temps caractéristique τ
du système :
-
On trace la
tangente à la courbe au point d'abscisse
t = 0 s et l'asymptote
horizontale
-
La constante de
temps τ est donnée par l'abscisse de leur point d'intersection.
-
-
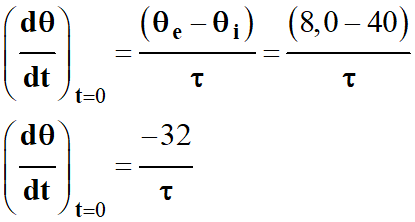
Détermination de
τA
-
Détermination de
τB
-
Représentation
graphique :
-
Pour l’expérience
A (courbe rouge),
τA
≈ 0,70 ks et
pour l’expérience
B (courbe bleue),
τB ≈ 0,24
ks.
-
ZOOM :
5.
Étude statistique :
-
Tableau de mesures
:
|
N° de l’expérience
|
1
|
2
|
3
|
4
|
5
|
6
|
|
τ
(s)
|
695
|
789
|
701
|
734
|
688
|
686
|
a.
Moyenne
 de la série de
mesures et l’incertitude-type u (τ) :
-
La moyenne
arithmétique
est le quotient de
la somme des valeurs x i par
le nombre total
de valeurs de la liste
n :
-
-
Écart à la moyenne
de chacune des valeurs :
-
Notation : l’écart
à la moyenne de chacune des valeurs est noté :
|
τ
i
|
695
|
789
|
701
|
734
|
688
|
686
|
|
|
715,5 ≈ 716
|
|
|
20,5
|
-73,5
|
14,5
|
-18,5
|
27,5
|
29,5
|
|
|
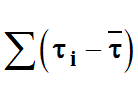
0
|
|
Qu’y a-t-il de
particulier ?
|
L’écart à la moyenne est un
nombre relatif.
Cette grandeur est positive,
négative
ou nulle
|
|
Était-ce
prévisible ?
Pourquoi ?
|
 :
La somme des écarts à la
moyenne est
égale à zéro.
|
|
Les écarts à la
moyenne sont des nombres relatifs.
On pourrait
utiliser les valeurs absolues.
On préfère
calculer les carrés des écarts à la moyenne.
|
|
|
420,3
|
5402
|
210,3
|
342,3
|
756,3
|
870,3
|
|
|
≈ 8002
|
-
Tableau Excel :
-
On remarque que
l’écart maximal est (– 73,5 s pour l’expérience N° 2) par rapport à
la
moyenne.
-
La variance var
est le quotient de la somme des carrés des écarts à la moyenne par
le
nombre n de l’effectif total.
-
La variance est la
moyenne arithmétique des carrés des écarts à la moyenne
arithmétique .
-
-
Variance de
l’échantillon.
-
-
L’écart-type
σ :
-
L'écart-type est
une mesure de la dispersion d’une série statistique autour de sa
moyenne
arithmétique.
-
L’écart-type est la
moyenne quadratique des écarts à la moyenne arithmétique :
-
-
-
L’écart-type σ
est égal à la racine carrée de la variance.
-
L’écart type
caractérise la dispersion des valeurs.
-
Affirmation :
-
En mathématique, on
constate que l’intervalle
 contient
plus de la moitié
des valeurs de la liste.
-
Valeur de l’écart-type :
-
-
L’expérience est
réalisée plusieurs fois dans les mêmes conditions pour vérifier
la
reproductibilité et éviter les erreurs grossières.
-
On remarque que les
valeurs sont assez dispersées.
-
La valeur de
l’expérience N° 2 (789) s’écarte
beaucoup de la valeur moyenne :
-
On peut calculer
l’écart-type standard :
-
-
Application
numérique :
-
-
Valeur de
l’incertitude-type u (τ) avec
l’écart-type standard σn-1
:
-
-
Application
numérique :
-
-
Valeur de
l’incertitude-type u (τ) avec
l’écart-type σ :
-
b.
Écriture de τA
sous la forme d’un encadrement.
-
-
τA = ( 716 ± 16 ) s ou τA
= ( 716 ± 15 ) s
-
700 s < τA < 732 s ou
701 s < τA
< 731 s
-
Les différentes
valeurs sont dispersées.
-
Si on supprime la
valeur de l’expérience N° 2 (789) :
-
Dans ce cas le
tableau Excel est le suivant :
-
La valeur moyenne :
-
Valeur de
l’incertitude-type u (τ) avec
l’écart-type standard σn-1
:
-
-
Application
numérique :
-
-
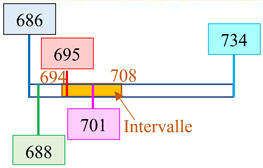
Encadrement : τA
= ( 701 ± 7 ) s
-
Dans ce cas, les
différentes valeurs sont moins dispersées.
6.
Qualité isolante du
plumage de canard.
-
L’expérience
A met en évidence le fait que les plumes de canards constituent
une
surface isolante.
-
La cloison remplie
de plumes réduit le flux thermique entre l’intérieur de la
boîte et le
milieu extérieur.
-
Ainsi si on
considère que le système atteint sa température d’équilibre
θe = 8,0 ° C au
bout de 5 τ,
-
Pour l’expérience
A, la durée est ΔtA
≈ 58 min environ ;
-
Alors que pour
l’expérience B, la durée est ΔtB
≈ 20 min environ.
|
