|
|
Mouvement et deuxième loi de Newton
Cours |
|
|
|
|
|
I- Vecteur position, vitesse et accélération. a)-
Le vecteur vitesse moyenne. b)- Le vecteur vitesse d'un point. a)-
Le vecteur variation de vitesse.
|
|
3)- Cas du
mouvement circulaire uniforme.
|
|
2)- Centre de
masse d’un système. 3)- Énoncé de la
deuxième loi de Newton. |
|
1)-
Chronophotographie du mouvement d’une balle.
QCM r
Les vecteurs position, vitesse et
accélération Des exemples de mouvements
La deuxième loi de Newton
|
|
1)- Exercice 04 page 228 : Déterminer les coordonnées d’un vecteur
accélération. 2)- Exercice 06 page 228 : Étudier un mouvement circulaire. 3)- Exercice 08 Page 229 : Exploiter les caractéristiques du vecteur
accélération. 4)- Exercice 10 page 229 :Tracer la trajectoire du centre de masse
d’un système. 5)- Exercice 12 page 229 : Appliquer la deuxième loi de Newton. 6)- Exercice 16 page 230 : Virage d’un avion. 7)- Exercice 17 page 230 : Saut au-dessus du canal de Corinthe. 8)- Exercice 21 page 231 : Le mouvement de Vénus. 9)- DS 01 : Le thermomètre de Galilée (34 min) : exercice 29 page
232. 10)- DS 02 : Un ascenseur à bateau (30 min) : exercice 30 page 235. 11)- Exercice : Préparation à ECE : Mesure de la viscosité d’une
huile de voiture.
|
|
QCM r
Les vecteurs position,
vitesse et accélération Des exemples de
mouvements
|
I- Vecteur position, vitesse et
accélération.
-
Avant de décrire le mouvement d’un
objet, il faut préciser :
-
Le système
S étudié
-
Et le référentiel
R d’étude.
-
l'objet
dont on étudie le mouvement est appelé le
mobile et l'objet de référence est appelé
le référentiel.
-
Un
référentiel est un
solide par rapport
auquel on étudie le mouvement d'un mobile.
-
Pour décrire le mouvement d'un mobile,
il faut indiquer le référentiel d'étude.
-
Un point matériel représente soit un
objet de petite taille (particule, petite bille), soit un objet de grande taille
dont on néglige les effets de rotation sur lui-même.
-
Généralement, on appelle cet objet le
mobile.
-
Le système est modélisé par un point
unique (c’est le centre de masse G
du système), on parle du modèle du point matériel de masse
m.
-
Lorsqu’on étudie le système
S de masse
m et de centre de
masse G, on
utilise la notation :
-
S = {m,
G}
-
Pour simplifier les écritures, l’étude
est limitée aux mouvements à deux dimensions, mais peut être généralisée aux
espaces à trois dimensions.
-
On travaille dans le repère orthonormé
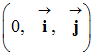 lié au référentiel choisi.
lié au référentiel choisi.
-
L’association du repère avec le
référentiel d’étude est notée : 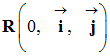
-
Le point
M (x, y) est repéré
grâce à ses coordonnées :
-
![]() ,
,
-
Les vecteurs
 sont des vecteurs
unitaires constants,
sont des vecteurs
unitaires constants,
![]() .
.
-
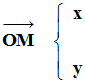
-
x (t)
et y (t)
, ou plus simplement
x et
y, sont les
coordonnées du point M
à l’instant t.
-
Unités : les coordonnées,
x et
y s’expriment en
mètres (m).
-
Les expressions
x (t)
et y (t)
sont appelées les équations horaires du mouvement.
-
![]()
-
Pour simplifier et alléger les
notations, on peut écrire : ![]()
-
Tout en sachant que
x et
y sont des
fonctions du temps t.
-
Valeur du vecteur position : ![]()
-
Repère :
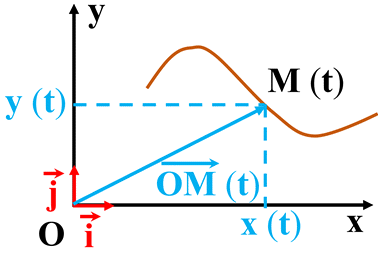
a)-
Le vecteur vitesse moyenne.
-
Expression du vecteur vitesse moyenne :
-

-
Que l’on peut aussi écrire en utilisant
le vecteur position :
-
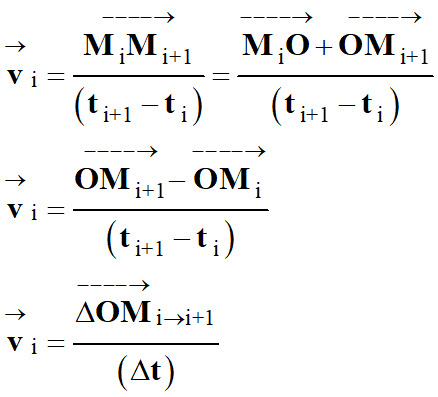
-
Il représente les variations du vecteur
position pendant l’intervalle de temps Δt.
b)-
Le vecteur vitesse d’un point.
-
Le vecteur vitesse d’un point en
position Mi
est la limite de :
-
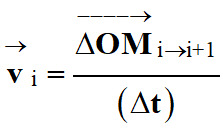 lorsque
Δt tend vers zéro.
lorsque
Δt tend vers zéro.
-
On écrit :
- 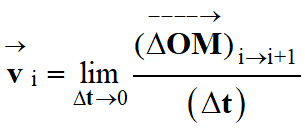
-
C’est la dérivée par rapport au temps
du vecteur position :
-
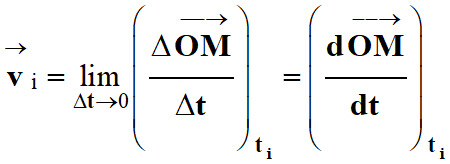
►
Définition :
| Dans un référentiel
R donné, le vecteur
vitesse
d’un point M à l’instant t, est égal à la dérivée, par rapport au temps, du vecteur position |
|
|
Ou plus simplement
|
|
|
Valeur en mètre (m) |
|
dt |
Valeur en seconde (s) |
|
|
Valeur en mètre par seconde (m . s–1) |
►
Coordonnées du vecteur vitesse :
-
Pour connaître les coordonnées du
vecteur vitesse, on dérive le vecteur position par rapport au temps :
|
|
|
|
|
Valeur du vecteur vitesse :
|
|
Vecteur position |
par rapport
au temps |
Vecteur vitesse |
|
|
|
►
Caractéristiques du vecteur vitesse.
-
Origine
: position occupée par le point mobile à l'instant
considéré t.
-
Direction
: tangente à la trajectoire au point considéré.
-
Sens
: celui du mouvement à cet instant.
-
Valeur
: celle de la vitesse instantanée à cet instant.
►
Représentation du vecteur vitesse.
-
On représente le vecteur vitesse par un
segment fléché :
-
Pour tracer ce vecteur vitesse :
|
-
Vecteur
vitesse du point mobile M à l'instant t3,
-
Origine
:
position occupée par le point mobile à l'instant considéré t
c'est-à-dire le point M3. - Direction : tangente à la trajectoire au point considéré : on peut tracer la
droite parallèle à (M2 M4)
issue de M3. -
Sens
: celui du mouvement à cet instant. -
Valeur
: celle de la vitesse instantanée à cet instant : -
-
Longueur du représentant
ℓv : -
Une échelle de
représentation est indispensable. -
Elle associe la longueur du
segment fléché à la valeur de la vitesse instantanée. -
Exemple : 1 cm ↔ 0,1 m . s–1.
- Dans le cas présent, on a enregistré la position du point mobile M, à intervalles de temps égaux très courts : - τ = 40 ms -
Pendant cette durée, le
mobile parcourt la distance M3M4
≈ 1,28 cm -
Valeur de la vitesse v3 : -
-
Le segment fléché aura une
longueur : ℓv3 =
3,2 cm. |
a)-
Le vecteur variation de vitesse.
-
Lors d’un mouvement, le vecteur vitesse
![]() d’un système peut varier en direction, en sens ou en valeur.
d’un système peut varier en direction, en sens ou en valeur.
-
Le vecteur variation de vitesse
![]() n’est
alors pas égal au vecteur nul.
n’est
alors pas égal au vecteur nul.
-
Le vecteur variation de vitesse
![]() d’un
système en mouvement entre deux positions Mi
et Mj
est défini par :
d’un
système en mouvement entre deux positions Mi
et Mj
est défini par :
-
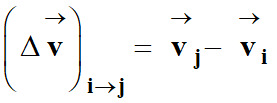
►
Tracé du vecteur variation de vitesse
![]()
Échelle : Échelle
pour la vitesse : 1 cm ↔ 0,1 m . s–1
-
Enregistrement : intervalle de temps
entre deux mesures : Δt
= τ = 40 ms
-
Schéma :
-
L’origine du vecteur est le point
B.
-
Longueur du représentant de 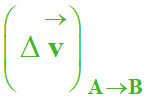 :
:
-
ℓΔv
≈ 1,4 cm
-
Valeur du vecteur variation de
vitesse 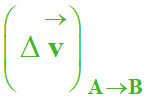 :
:
-
(Δv)A→B
≈ 0,14 m . s–1
-
Par analogie avec le vecteur vitesse,
on peut déterminer le vecteur accélération à un instant
ti+1 :
-
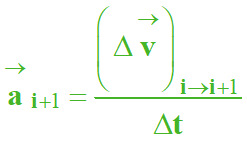 avec
A qui représente
i et
B qui représente
i + 1
avec
A qui représente
i et
B qui représente
i + 1
- 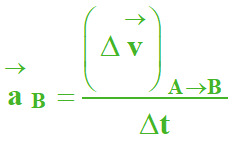
-
Valeur de l’accélération :
-
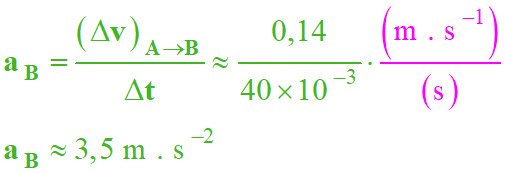
-
Longueur du représentant ℓa
:
-
Une échelle de représentation est
indispensable.
-
Elle associe la longueur du segment
fléché à la valeur de l’accélération.
-
Échelle :
-
Longueur du représentant :
ℓaB ≈
3,5 cm
-
Caractéristiques du vecteur
accélération ![]() :
:
-
Origine : le point
B (point d’indice (i
+ 1))
-
Direction et sens : 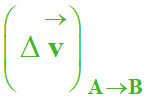
-
Valeur : 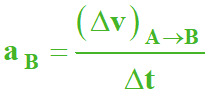
-
Longueur avec l’échelle choisie :
ℓaB ≈
3,5 cm
-
Représentation :
-
Le vecteur accélération traduit les
variations du vecteur vitesse.
-
Comme pour le vecteur vitesse :
-
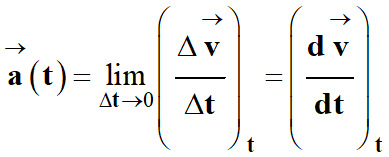
-
Dans un référentiel
R donné, le vecteur
accélération
![]() d’un point M
à l’instant t,
est égal à la dérivée , par rapport au temps, du vecteur vitesse
d’un point M
à l’instant t,
est égal à la dérivée , par rapport au temps, du vecteur vitesse
![]() à cet
instant :
à cet
instant :
|
|
Ou plus simplement
|
|
|
Valeur en mètre (m . s–1) |
|
dt |
Valeur en seconde (s) |
|
|
Valeur en
mètre par seconde au carré (m . s–2) |
c)-
Coordonnées du vecteur accélération.
-
Pour connaître les coordonnées du
vecteur accélération, on dérive le vecteur vitesse par rapport au temps :
|
|
|
|
|
Valeur du
vecteur accélération :
|
|
Vecteur vitesse |
par rapport
au temps |
Vecteur accélération |
|
|
|
-
Remarque :
|
Comme |
|
Alors |
|
|
=> |
|
d)-
Caractéristiques du vecteur accélération.
-
Expression approchée du vecteur
accélération :
-
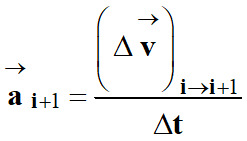
-
Considérons le vecteur accélération :![]()
-
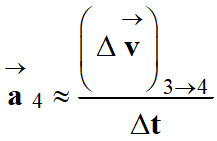
-
Origine : le point
M4
-
Direction et sens : le vecteur
accélération est colinéaire et de même sens que le vecteur variation de vitesse
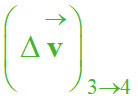
-
Valeur : 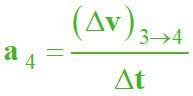
-
Longueur avec l’échelle choisie :
ℓa4 ≈
3,5 cm
-
Récapitulatif :
|
Vecteur
position |
Vecteur
vitesse |
Vecteur
accélération |
|
|
|
|
-
On donne les équations paramétriques
horaires du mouvement d’un point M
dans le repère
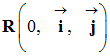 :
:
-
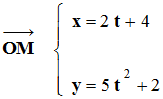
-
Donner l’expression des coordonnées du
vecteur vitesse et du vecteur accélération du point mobile
M dans le repère
R.
|
Vecteur position |
Vecteur vitesse |
Vecteur accélération |
|
|
|
|
-
Remarque :
-
La valeur de l’accélération est reliée
aux coordonnées du vecteur accélération ax
et ay
par la relation de Pythagore :
-
![]()
-
Les coordonnées et la valeur du vecteur
accélération dépendent du temps et dépendent comme le vecteur vitesse du
référentiel d’étude.
-
Un point mobile
M est animé d’un
mouvement rectiligne si sa trajectoire est une portion de droite.
b)-
Caractéristiques graphiques du mouvement
rectiligne uniforme.
|
Chronophotographie
d’un mouvement
rectiligne |
|
|
Représentation
graphique
de la coordonnée x
de la position en
fonction du temps
Le coefficient directeur
de la portion de droite
tracée est égal à la
valeur de la vitesse v
du mobile. |
|
|
Représentation
graphique
de la coordonnée vx
de la vitesse en
fonction du temps |
|
|
Représentation
graphique
de l’accélération ax
en fonction du temps |
|
|
Vecteur
position |
Vecteur
vitesse |
Vecteur
accélération |
|
|
|
|
|
|
Équations
horaires |
x
(t) = v0x . t + x0 |
vx
(t) = v0x |
ax
(t) = 0 |
c)-
Les mouvements
rectilignes uniformément variés.
-
Dans un référentiel donné, un système
est animé d’un mouvement rectiligne uniformément varié si son vecteur
accélération a toujours la même direction, le même sens et la même valeur.
-
Le vecteur accélération est un vecteur
constant au cours du temps : ![]()
-
La trajectoire est une portion de
droite
-
La valeur de l’accélération est
constante au cours du temps.
-
Le vecteur position, le vecteur vitesse
et le vecteur accélération ont même direction.
-
La valeur de la vitesse est une
fonction affine du temps : vx
= a
x0 .
t +
v0x
►
Caractéristiques graphiques du
mouvement rectiligne uniformément varié.
-
Les équations horaires :
|
|
Vecteur
position |
Vecteur
vitesse |
Vecteur
accélération |
|
|
|
|
|
|
Équations
horaires |
|
vx
(t) = a0x . t + v0x |
ax
(t) = a0x |
-
Un point mobile
M est animé d’un
mouvement circulaire si sa trajectoire est une portion de cercle.
-
Ce repère est bien utile pour l’étude
des mouvements circulaires (uniformes)
-
Considérons un point mobile
M animé d’un
mouvement circulaire uniforme.
-
La trajectoire est un cercle de centre
O et de
rayon R
et la valeur de la vitesse ne change pas au cours du temps.
-
Pour simplifier l’étude d’un tel
mouvement et en déduire les caractéristiques, il faut utiliser le repère de
Frenet :
-
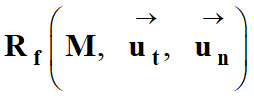
-
![]() : désigne
un vecteur unitaire tangent à la trajectoire et orienté dans le sens du
mouvement.
: désigne
un vecteur unitaire tangent à la trajectoire et orienté dans le sens du
mouvement.
-
![]() : désigne
un vecteur unitaire perpendiculaire à
: désigne
un vecteur unitaire perpendiculaire à
![]() et orienté vers le centre
O du cercle.
et orienté vers le centre
O du cercle.
|
|
|
-
Le vecteur vitesse est tangent à la
trajectoire au point considéré
![]() .
.
-
Le vecteur vitesse change de direction
à chaque instant.
-
Pour obtenir les coordonnées du vecteur
accélération, il faut dériver cette expression par rapport au temps.
- 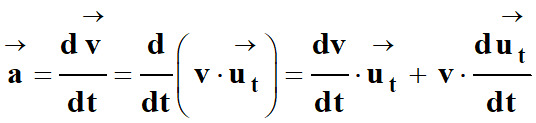 (1) ceci se dérive comme un produit.
(1) ceci se dérive comme un produit.
-
Le vecteur accélération peut se
décomposer de la façon suivante :
-
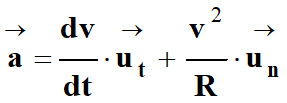
-
En conséquence, le vecteur accélération
peut être décomposé en une :
-
Accélération tangentielle
![]() qui dépend de la variation de la valeur de la vitesse :
qui dépend de la variation de la valeur de la vitesse :
-
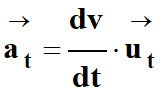 avec
avec 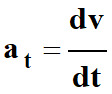
-
Accélération normale
![]() qui est liée à la variation de la direction du vecteur vitesse.
qui est liée à la variation de la direction du vecteur vitesse.
-
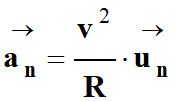 avec
avec 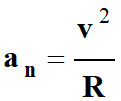
-
Autre expression du vecteur
accélération :
-
![]()
►
Remarque :
-
À ce niveau, on peut donner une petite
explication :
-
Le vecteur
![]() est un vecteur unitaire :
est un vecteur unitaire :
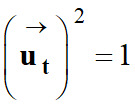
-
Étude de la dérivée par rapport au temps
de
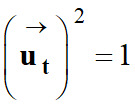 :
:
-
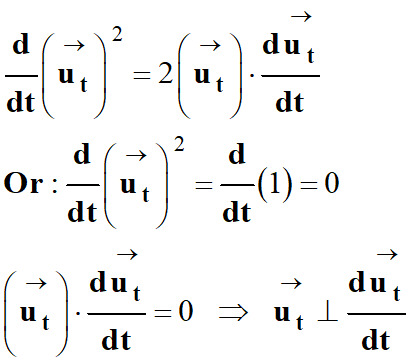
3)- Cas du mouvement circulaire uniforme.
-
Dans un référentiel donné, un système
est animé d’un mouvement circulaire uniforme si sa trajectoire est une portion
de cercle de rayon R
et si la valeur de sa vitesse v
est constante.
-
Le vecteur accélération est alors
centripète et sa valeur a
est constante.
-
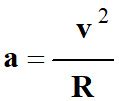
-
Le mobile parcourt des arcs égaux
pendant des durées égales.
-
Exemple :
|
Le mobile
autoporteur, maintenu par un fil tendu, est lancé sur la
table à digitaliser. La table est
horizontale. On enregistre la
position du centre d’inertie du solide à
intervalles de temps égaux
t
après avoir lâché le mobile. |
-
Le vecteur vitesse est à chaque instant
perpendiculaire au vecteur accélération.
-
Le vecteur vitesse et le vecteur
accélération changent de direction à chaque instant.
►
Récapitulatif :
|
Mouvement |
Circulaire uniforme |
|
Vecteur vitesse
|
Direction :
variable et tangente à la trajectoire |
|
Sens : celui du mouvement |
|
|
Valeur : v = constante |
|
|
Unité : m . s–1 |
|
|
Vecteur accélération :
|
Direction :
variable et perpendiculaire à la trajectoire |
|
Sens : vers le centre de la trajectoire |
|
|
Valeur : |
|
|
Unités :
v :
m . s–1 ; R : m et a : m . s–2 |
4)-
Les mouvements circulaires non
uniformes.
a)-
Exemple : Mouvement d’un pendule simple.
-
Un pendule simple est constitué d’un
objet sphérique de masse m
suspendu à un fil inextensible de longueur ℓ.
-
Remarque : la masse du fil est
négligeable devant celle de l’objet.
-
La longueur
ℓ est grande devant
celle de l’objet.
-
Dans le cas contraire, on dit que le
pendule est pesant.
-
On écarte le solide de sa position
d’équilibre d’un angle θ0
< 10°.
-
On laisse le pendule osciller librement
et on fait une représentation à un temps t
quelconque.
- Vidéo : Vidéo (Forces ) et Vidéo (Accélération et vitesse)
-
Dans un référentiel donné, un système
est animé d’un mouvement circulaire non uniforme,
-
Si sa trajectoire est une portion de
cercle de rayon R
-
Et si la valeur de l’accélération n’est
pas constante.
-
À chaque instant, le vecteur
accélération
![]() se décompose en deux vecteurs :
se décompose en deux vecteurs :
-
![]()
|
Vecteur
accélération |
|
Le vecteur
accélération
tangentielle |
Le vecteur
accélération
normale |
|
|
|
|
|
|
Direction |
Tangent à la trajectoire au point considéré |
Centripète |
|
|
Sens |
Orienté dans le sens du mouvement |
Orienté vers le
centre du cercle |
|
|
Valeur |
C’est la dérivée par rapport au temps de la valeur de
la vitesse v |
|
►
Récapitulatif :
|
Mouvement |
Circulaire uniforme non uniforme |
|
Vecteur vitesse
|
Direction :
variable et tangente à la trajectoire |
|
Sens : celui du mouvement |
|
|
Valeur : v = variable |
|
|
Unité : m . s–1 |
|
|
Vecteur accélération :
ou
|
Direction :
variable et non perpendiculaire à la trajectoire |
|
Sens : vers l’intérieur de la trajectoire |
|
|
Valeur :
|
|
|
Unités :
v :
m . s–1 ; R : m et a : m . s–2 |
►
Remarque :
-
Si l’accélération tangentielle est
nulle, alors
![]() , donc la vitesse v
= constante et le mouvement est circulaire uniforme.
, donc la vitesse v
= constante et le mouvement est circulaire uniforme.
►
Définition :
-
Un référentiel galiléen est un
référentiel dans lequel le principe de l’inertie est vérifié.
►
Le référentiel terrestre ou référentiel
du laboratoire.
-
On utilise, le plus souvent, comme
repère lié au référentiel terrestre, deux axes horizontaux et un axe vertical.
-
Ce référentiel est bien commode pour
l’étude du mouvement des objets dans une salle de classe, pour tous les
mouvements qui s’effectuent au voisinage de la terre.
-
Si l’expérience est
suffisamment courte, on peut considérer que ce référentiel est galiléen avec une
bonne approximation (précision de l’ordre de 10–2
à 10–3).
►
Le référentiel géocentrique.
-
L’origine du repère lié au
référentiel Géocentrique
est située au centre de la Terre.
-
L’axe
z’Oz est orienté
vers une étoile lointaine : on peut choisir l’étoile polaire.
-
Les axes
x’Ox et
y’Oy sont situés
dans le plan équatorial et ils sont orientés vers des étoiles lointaines
supposées fixes.
-
Ce référentiel est commode pour l’étude
des satellites de la Terre.
-
Ce référentiel n’est pas entraîné dans
le mouvement de rotation de la Terre.
-
Dans ce référentiel,
-
On peut considérer que
ce référentiel est galiléen avec une bonne approximation ( précision de l’ordre
de 10–3 à 10–4)
►
Le référentiel héliocentrique ou de
Copernic.
-
L’origine du repère lié au
référentiel Héliocentrique
est située au centre du Soleil.
-
Les axes
z’Oz,
x’Ox et
y’Oy sont
orthogonaux et ils sont orientés vers des étoiles lointaines supposées fixes.
-
Ce référentiel est commode pour l’étude
des satellites du Soleil.
-
Dans ce référentiel,
-
On peut considérer que
ce référentiel est galiléen avec une très bonne approximation (précision de
l’ordre de 10–10)
2)- Centre de masse
G d’un système.
-
Le centre de masse
G d’un système est
l’unique point de ce système où peut toujours s’appliquer le principe d’inertie.
-
On ramène l’étude du mouvement d’un
système à celle de son centre de masse G.
-
On considère que toute la masse
m du système est
concentrée en G.
►
Exemple : mouvement d’un palet
autoporteur sur une table horizontale :
-
Un mobile autoporteur est lancé sur une
table horizontale.
-
Il est muni de deux dispositifs de
marquage :
-
Le premier sur son centre de masse
G
-
Le second coïncidant avec le point
A à la
périphérie du mobile.
-
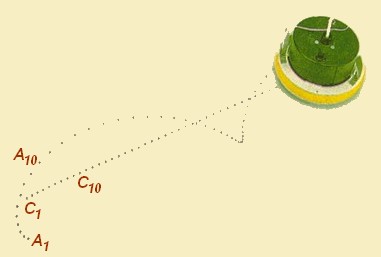
On enregistre les positions successives
des points G
et A
à intervalles de temps τ
= 20 ms.
-
On obtient l’enregistrement suivant.
| -
Au cours du mouvement du mobile
autoporteur, le centre de masse G a un mouvement plus simple (mouvement rectiligne uniforme) que celui du point A situé à sa périphérie (mouvement curviligne varié : Cycloïde) |
- Autre Vidéo :

3)- Énoncé de la deuxième loi de Newton.
a)-
Relation approchée (classe de
première) :
|
- Dans un référentiel donné, si un système de masse m constante est soumis à une ou plusieurs forces constantes,
le vecteur variation
de vitesse et la somme de
ces vecteurs forces
|
|
|
Valeur de la
force F en newton (N) |
|
Valeur de la
masse m en kilogramme (kg) |
|
|
Valeur de la
durée Δt en seconde (s) |
-
Ces deux vecteurs sont colinéaires.
-
La somme vectorielle des forces qui
s’exercent sur un système
![]() est également appelée résultante des forces notée :
est également appelée résultante des forces notée :
-
![]()
-
Plus la masse d’un système est grande
et plus il est difficile de modifier le mouvement de ce système.
-
Si Δt
→ 0, et la relation devient :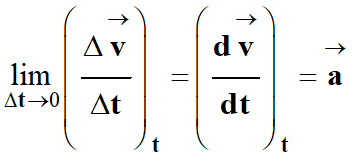
-
![]()
|
Dans un référentiel galiléen, la somme des vecteurs
forces
appliquées à un
système S, de masse
m et de centre de masse G,
est égal au
produit de sa masse m par
le vecteur accélération
de son centre de
masse. |
|
|
Valeur des
forces F en newton (N) |
|
Valeur de la
masse m en kilogramme (kg) |
|
|
Valeur de l’accélération aG en mètre par seconde au carré (m
. s–2) |
-
Schéma :
-
La deuxième loi de Newton permet de
déterminer le vecteur accélération
![]() du centre de masse à partir des forces
du centre de masse à partir des forces
![]() appliquées au système ou inversement.
appliquées au système ou inversement.
c)-
Cas d’un système immobile.
-
Cas particulier du système immobile :
![]()
-
Il découle de ceci que : ![]()
-
Ceci traduit le Principe d’inertie
(première loi de Newton).
-
Le principe d’inertie apparaît comme un
cas particulier de la deuxième loi de Newton.
1)- Chronophotographie du mouvement d’une balle.

|
QCM r
Les vecteurs position,
vitesse et accélération Des exemples de
mouvements |
|
1)- Exercice 04 page 228 : Déterminer les coordonnées d’un vecteur
accélération. 2)- Exercice 06 page 228 : Étudier un mouvement circulaire. 3)- Exercice 08 Page 229 : Exploiter les caractéristiques du vecteur
accélération. 4)- Exercice 10 page 229 :Tracer la trajectoire du centre de masse
d’un système. 5)- Exercice 12 page 229 : Appliquer la deuxième loi de Newton. 6)- Exercice 16 page 230 : Virage d’un avion. 7)- Exercice 17 page 230 : Saut au-dessus du canal de Corinthe. 8)- Exercice 21 page 231 : Le mouvement de Vénus. 9)- DS 01 : Le thermomètre de Galilée (34 min) : exercice 29 page
232. 10)- DS 02 : Un ascenseur à bateau (30 min) : exercice 30 page 235. 11)- Exercice : Préparation à ECE : Mesure de la viscosité d’une
huile de voiture.
|
|
|