|
Mouvement et deuxième loi de Newton |
|
|
|
|
|
|
QCM N° 11
Mouvement et
deuxième loi de Newton
Les vecteurs
position, vitesse et accélération
Des exemples de
mouvements
La deuxième loi
de Newton.
Pour chaque
question, indiquer la (ou les) bonne(s) réponse(s). |
|||||
|
A : Un motard effectue un essai sur une ligne rectiligne. M est un point du système
{moto et motard} d’abscisse x. |
B :
On a représenté les positions à intervalles de
temps réguliers d’un point P
pris sur le plateau horizontal d’un manège en
mouvement de rotation
autour d’un axe vertical.
|
||||
|
|
Énoncé |
A |
B |
C |
R |
|
1 |
Dans la
situation
A, la distance parcourue par
la moto 3 s après le départ
est : |
d
= 20,7 m |
d
= 6,9 m |
d
= 10,4 m |
A |
|
2 |
Dans la situation A, la vitesse de la moto est donnée par la relation : |
v
(t) = 2,3 t |
v
(t) = 4,6 t |
v
(t) = 4,6 t + 2,3 |
B |
|
3 |
Dans la
situation
B, le vecteur vitesse
|
Est un
vecteur
constant |
A une
valeur
constante |
Varie au
cours
du temps |
BC |
|
4 |
D’après la situation B, le vecteur accélération
point P : |
Est dirigé
vers le
centre de
la trajectoire |
A une
valeur égale
à |
A une
valeur égale
à
avec R
le rayon
du cercle |
AC |
|
5 |
Dans la
situation
A, le mouvement du
point M du système est :
|
Rectiligne
uniforme |
Rectiligne
uniformément
accéléré |
Curviligne
varié |
B |
|
6 |
Dans la
situation
B, le mouvement du
point P du système est
circulaire : |
uniforme |
Uniformément
accéléré |
Uniformément
retardé |
A |
|
7 |
Le centre de
masse G d’un système :
|
Est un point
quelconque
choisi d’un
système |
Est le seul
point du
système où peut toujours
s’appliquer
le principe
d’inertie |
a en général
un mouvement
plus simple
que les autres
points |
BC |
|
8 |
La deuxième
loi de Newton est donnée par
la relation : |
|
|
|
AB |
|
9 |
Dans la situation B, la somme des forces appliquées au point P est : |
Colinéaire
et de même
sens que
le vecteur
accélération |
Perpendiculaire
et de même
sens que
le vecteur
accélération |
Dirigée vers
le centre
de la
trajectoire |
AC |
|
10 |
Lorsqu'un système est animé d'un mouvement circulaire
uniforme |
Son vecteur
vitesse est
constant |
Son vecteur
accélération
est constant |
Son vecteur
accélération
est centripète |
C |
QCM réalisé avec le logiciel Questy
Pour s’auto-évaluer
Vecteur position.
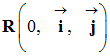
![]() ou
ou 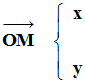
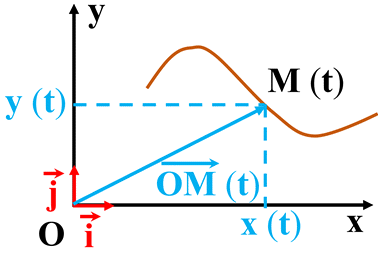
Le vecteur vitesse moyenne

Le vecteur vitesse d’un point :![]()
►
Définition :
| Dans un référentiel R donné, le vecteur vitesse
d’un point M à l’instant t, est égal à la dérivée, par rapport au temps, du vecteur position |
|
|
Ou plus simplement
|
|
|
Valeur en mètre (m) |
|
dt |
Valeur en seconde (s) |
|
|
Valeur en mètre par seconde (m . s–1) |
►
Coordonnées du vecteur vitesse :
-
Pour connaître les coordonnées du vecteur vitesse, on dérive le
vecteur position par rapport au temps :

|
|
|
|
|
Valeur du vecteur vitesse :
|
►
Caractéristiques du vecteur vitesse.
Vecteur accélération :![]()
►
Définition.
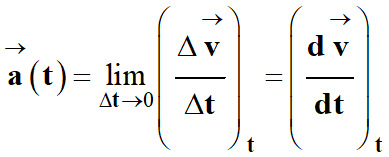
| Dans un référentiel R donné, le vecteur accélération
est égal à la dérivée , par rapport au temps, du vecteur vitesse |
|
|
Ou plus simplement
|
|
|
Valeur en mètre (m . s–1) |
|
dt |
Valeur en seconde (s) |
|
|
Valeur en
mètre par seconde au carré (m . s–2) |
►
Coordonnées du vecteur accélération.
-
Pour connaître les coordonnées du vecteur accélération, on dérive
le vecteur vitesse par rapport au temps :
|
|
|
|
|
Valeur du
vecteur accélération :
|
Récapitulatif :
|
Vecteur
position |
Vecteur
vitesse |
Vecteur
accélération |
|
|
|
|
Caractéristiques graphiques du mouvement rectiligne
uniforme :
|
Chronophotographie
d’un mouvement
rectiligne
|
|
|
Représentation
graphique
de la coordonnée x
de la position en
fonction du temps
Le coefficient directeur
de la portion de droite
tracée est égal à la
valeur de la vitesse v
du mobile. |
|
|
Représentation
graphique
de la coordonnée vx
de la vitesse en
fonction du temps |
|
|
Représentation
graphique
de l’accélération ax
en fonction du temps |
-
Les équations horaires :
|
|
Vecteur position |
Vecteur vitesse |
Vecteur accélération |
|
|
|
|
|
|
Équations horaires |
x
(t) = v0x . t + x0 |
vx
(t) = v0x |
ax
(t) = 0 |
Caractéristiques graphiques du mouvement rectiligne
uniformément varié :
-
Les équations horaires :
|
|
Vecteur position |
Vecteur vitesse |
Vecteur accélération |
|
|
|
|
|
|
Équations
horaires |
|
vx
(t) = a0x . t + v0x |
ax
(t) = a0x |
Mouvement circulaire uniforme :
|
Mouvement |
Circulaire uniforme |
|
Vecteur vitesse
|
Direction : variable et tangente à la trajectoire |
|
Sens : celui du mouvement |
|
|
Valeur : v = constante |
|
|
Unité : m . s–1 |
|
|
Vecteur accélération :
|
Direction : variable et perpendiculaire à la trajectoire |
|
Sens : vers le centre de la trajectoire |
|
|
Valeur : |
|
|
Unités :
v :
m . s–1 ; R : m et a : m . s–2 |
Les mouvements circulaires non uniformes :
|
Vecteur
accélération |
|
Le vecteur accélération
tangentielle |
Le vecteur accélération
normale |
|
|
|
|
|
|
Direction |
Tangent à la trajectoire au point considéré |
Centripète |
|
|
Sens |
Orienté dans le sens du mouvement |
Orienté vers
le centre du cercle |
|
|
Valeur |
C’est la dérivée par rapport au temps de la valeur de
la vitesse v |
|
►
Récapitulatif :
|
Mouvement |
Circulaire uniforme non uniforme |
|
Vecteur vitesse
|
Direction : variable et tangente à la trajectoire |
|
Sens : celui du mouvement |
|
|
Valeur : v = variable |
|
|
Unité : m . s–1 |
|
|
Vecteur accélération :
ou
|
Direction :
variable et non perpendiculaire à la trajectoire |
|
Sens : vers l’intérieur de la trajectoire |
|
|
Valeur :
|
|
|
Unités :
v :
m . s–1 ; R : m et a : m . s–2 |
Référentiel Galiléen.
►
Définition :
Centre de masse d’un système.
Énoncé de la deuxième loi de Newton :
|
Dans un référentiel galiléen, la somme des
forces appliquées à un
système S, de masse m et de centre de masse G,
est égal au produit
de sa masse m par le vecteur accélération de son centre de
masse. |
|
|
Valeur des
forces F en newton (N) |
|
Valeur de la
masse m en kilogramme (kg) |
|
|
Valeur de
l’accélération aG en mètre par seconde au carré
(m . s–2) |
|
|