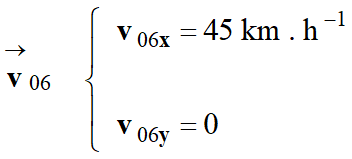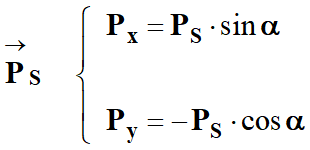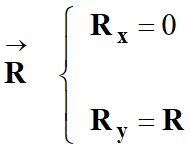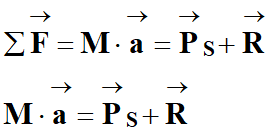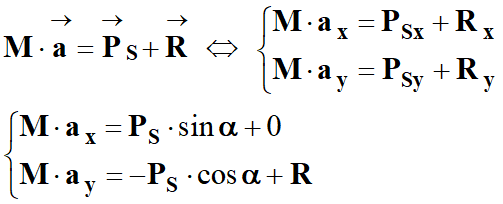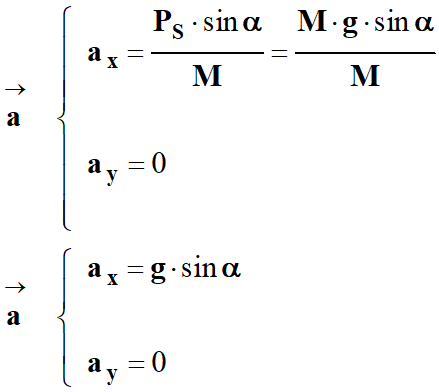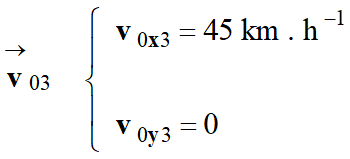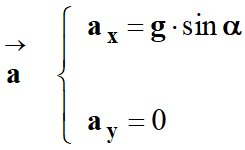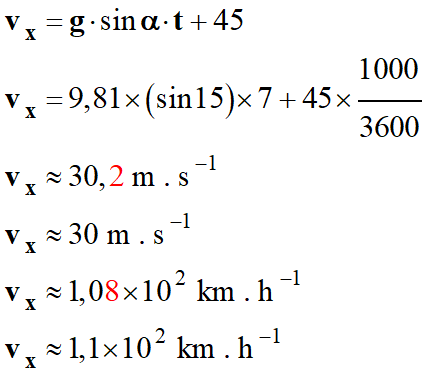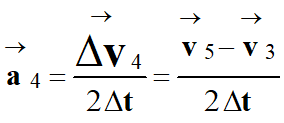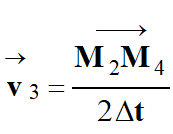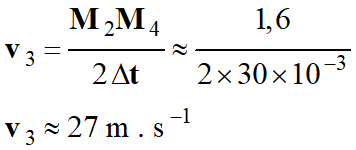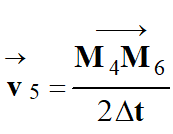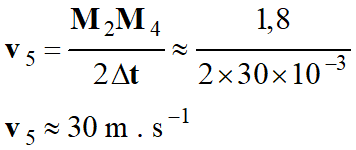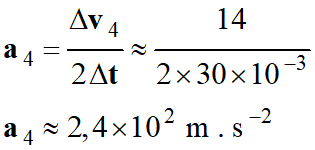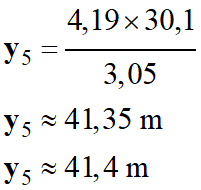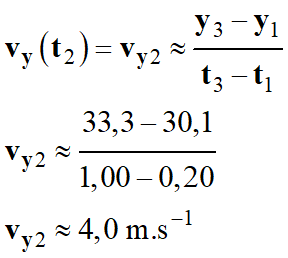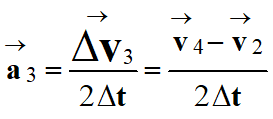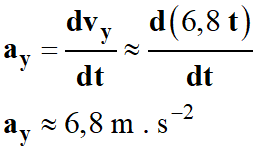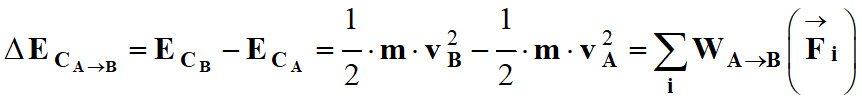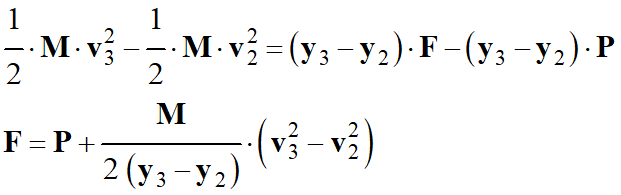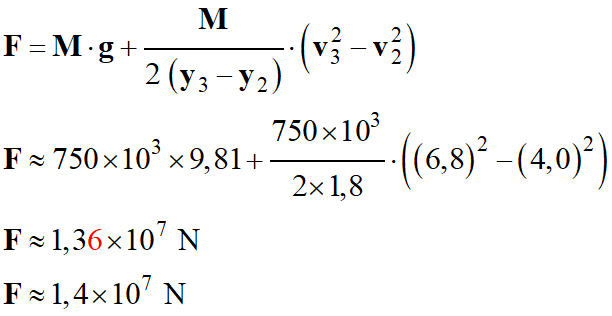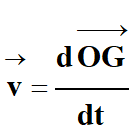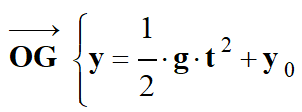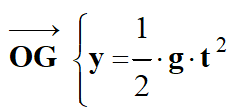Chap. N° 11 Exercices 24 : Mouvement et deuxième loi de Newton
|
Chap. N° 11

|
Mouvement et deuxième loi de Newton
Exercices 2024
Cours
Exercices
|
|
|
|
|
|
I-
Exercice : Chute de Philae.
1)- Énoncé.

https://rosetta.cnes.fr/fr
Le 12 novembre 2014, à la date t = 0 s,
l'atterrisseur Philae s'est détaché de la sonde Rosetta pour effectuer une chute
libre de 20 km, sans vitesse initiale, et se poser sur la comète 67P/
Tchourioumov - Guérassimenko.
Cette descente a duré plusieurs heures.
Philae est considéré pour chute libre, c’est-à-dire
qu'il n'est soumis qu'à son poids.
L'axe Oy
utilisé pour l'étude est vertical dirigé vers le haut, l'origine étant au niveau
du sol de la comète.
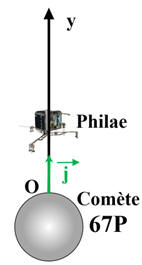
Le champ de pesanteur de la comète est considéré comme
uniforme, d'intensité moyenne :
g = 1,5 × 10–5
N . kg–1.
a)-
En utilisant la deuxième loi de Newton,
dans le référentiel de la comète supposé galiléen, déterminer les coordonnées du
vecteur accélération
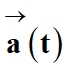 de
Philae.
de
Philae.
b)-
Préciser le type de mouvement effectué
par Philae. Justifier.
c)-
Le vecteur position
 de
l'atterrisseur a pour coordonnée :
de
l'atterrisseur a pour coordonnée :
-
y (t)
= b .
t2
+ c
avec b = – 7,50 × 10–6
m . s–2
et c
= 20000 m
-
En déduire la coordonnée du
vecteur vitesse
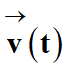 ,
puis
retrouver la coordonnée du vecteur accélération
,
puis
retrouver la coordonnée du vecteur accélération
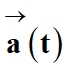 .
.
d)-
À l’aide du vecteur position
 , terminer la
durée de chute Δt de Philae.
, terminer la
durée de chute Δt de Philae.
e)-
La durée réelle de la chute est de 7 h.
Dans le modèle utilisé, quelles sont les hypothèses discutables ? Justifier.

2)- Correction.
a)-
Coordonnées du vecteur accélération
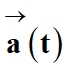 de
Philae.
de
Philae.
-
Deuxième loi de Newton :
|
Dans un référentiel galiléen, la
somme des vecteurs forces 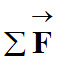
appliquées à un
système S, de masse m et de centre de masse G,
est égal au
produit de sa masse m par le vecteur accélération
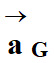
de son centre de
masse.
|
|
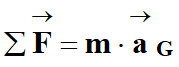
|
Valeur des
forces F en newton (N)
|
|
Valeur de la
masse m en kilogramme (kg)
|
|
Valeur de
l’accélération aG en mètre par
seconde au carré
(m . s–2)
|
-
Référentiel d’étude : Référentiel de la comète
supposé galiléen
-
Repère
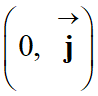 lié au
référentiel de la Comète
lié au
référentiel de la Comète
-
Bilan des forces : Philae est considéré en chute
libre,
-
Il n'est soumis qu'à son poids :

-
Schéma du mobile à l’instant
t :
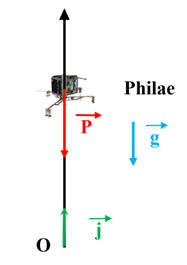
-
La deuxième loi de Newton appliquée au système
S, dans le référentiel
galiléen permet d’écrire :
-
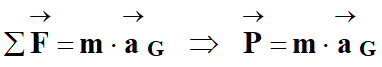
-
Comme :
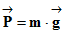
-
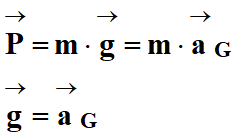
-
En utilisant les notations de l’énoncé :
-
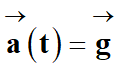
-
Le vecteur accélération
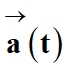 est vertical et orienté
vers le bas
est vertical et orienté
vers le bas
-
Coordonnées du vecteur accélération
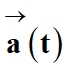 :
:
-
ay
= – g
-
ay
= – 1,5 × 10–5
N . kg–1
-
ay
= – 1,5 × 10–5
m . s–2
b)-
Type de mouvement effectué par Philae.
-
ay
= – g = cte
-
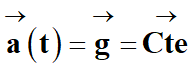
-
Le vecteur accélération
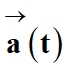 est un vecteur constant
(même direction, sens et valeur à chaque instant) :
est un vecteur constant
(même direction, sens et valeur à chaque instant) :
-
Le mobile est animé d’un mouvement rectiligne
uniformément accéléré suivant l’axe Oy.
c)-
Coordonnée du vecteur vitesse
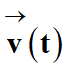 ,
,
►
Première méthode : (celle associée à l’énoncé)
-
Le vecteur position
 de
l'atterrisseur a pour coordonnée :
de
l'atterrisseur a pour coordonnée :
-
y (t)
= b .
t2 +
c avec
b = – 7,50 × 10–6
m . s–2 et
c = 20000 m
-
Le vecteur vitesse
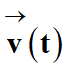 est la dérivée par rapport au
temps du vecteur position
est la dérivée par rapport au
temps du vecteur position
 .
.
-
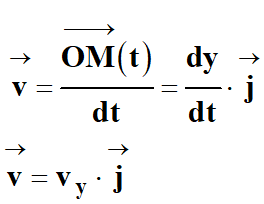
-
Coordonnée du vecteur vitesse
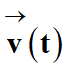 :
:
-
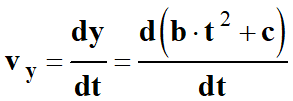
-
On dérive l’expression par rapport au temps.
-
Comme b
et c sont des
constantes :
-
vy
(t) = 2
b . t
avec b
= – 7,50 × 10–6 m . s–2
-
Le vecteur accélération
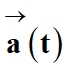 est la dérivée par rapport au
temps du vecteur vitesse
est la dérivée par rapport au
temps du vecteur vitesse
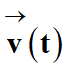 .
.
-
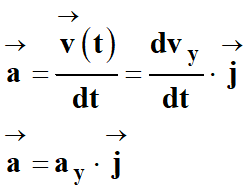
-
Coordonnée du vecteur accélération
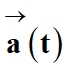 .
.
-
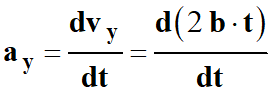
-
On dérive l’expression par rapport au temps.
-
ay
(t) = 2
b avec b
= – 7,50 × 10–6 m . s–2
-
ay
(t) = 2 × (– 7,50 × 10–6)
-
ay
(t) ≈ – 1,50 × 10–5
m . s–2
-
ay
(t) ≈ – g
-
on retrouve bien la coordonnée
ay du
vecteur accélération 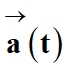 trouvé à la question a)-.
trouvé à la question a)-.
►
Seconde méthode :
-
On part du vecteur accélération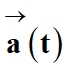 de la question
a)- :
de la question
a)- :
-
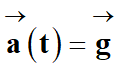
-
Le vecteur accélération
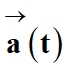 est vertical et orienté
vers le bas
est vertical et orienté
vers le bas
-
Coordonnées du vecteur accélération :
-
ay
= – g
-
ay
= – 1,5 × 10–5
N . kg–1
–
ay
= – 1,5 × 10–5
m . s–2
►
Conditions initiales :
-
Au temps t
= 0 :
-
Au temps t
= 0 s, la coordonnée du point mobile M,
centre de masse de Philae est :
-
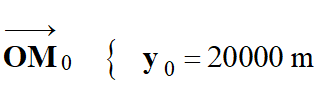
-
Au temps t
= 0, la vitesse initiale est nulle :
-
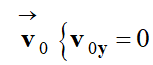
►
À partir du vecteur accélération
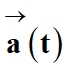 , on peut atteindre
le vecteur vitesse
, on peut atteindre
le vecteur vitesse 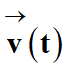 :
:
-
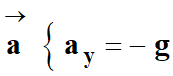
-
Le vecteur accélération
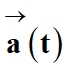 est la dérivée par rapport au
temps du vecteur vitesse
est la dérivée par rapport au
temps du vecteur vitesse
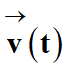 .
.
-
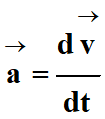
-
La détermination du vecteur vitesse
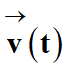 nécessite de
rechercher la primitive par rapport au temps de chaque coordonnée du vecteur
accélération
nécessite de
rechercher la primitive par rapport au temps de chaque coordonnée du vecteur
accélération
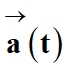 en tenant compte des conditions initiales.
en tenant compte des conditions initiales.
-
On cherche les primitives des équations
précédentes.
-
Il apparaît des constantes qui sont liées aux
conditions initiales.
-
Les constantes d’intégration apparues dans les
primitives sont liées aux conditions initiales :
-
c’est-à-dire les coordonnées du vecteur vitesse
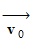 à l’instant initial.
à l’instant initial.
|
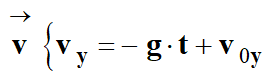
|
D’après les
conditions initiales
|
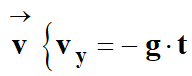
|
-
Le vecteur vitesse
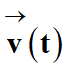 est la dérivée par rapport au
temps du vecteur position
est la dérivée par rapport au
temps du vecteur position
 .
.
-

-
On opère de la même façon :
|
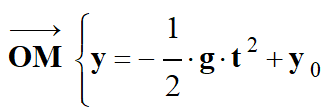
|
D’après les
conditions initiales
|
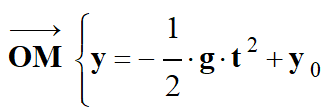
|
-
Avec : g
= – 1,50 × 10–5 m . s–2
et y0
= 20000 m
-
y (m) = – 7,50 × 10–6
t2
+ 20000
d)-
Durée de chute Δt
de Philae.
-
Le vecteur position
 de
l'atterrisseur a pour coordonnée :
de
l'atterrisseur a pour coordonnée :
-
y (t)
= b .
t2 +
c avec
b = – 7,50 × 10–6
m . s–2 et
c = 20000 m
-
Pendant la durée Δt
Philae passe de la position initiale (y0
= 20000 m) à la position O (
y = 0 )
-
Δt = t – t0
-
Avec t0
= 0
-
Δt = t
-
y (Δt)
= b . (Δt)2
+ c = 0
-
Il faut résoudre cette équation :
-
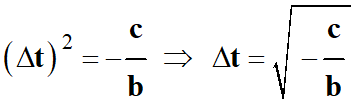
-
Application numérique :
-
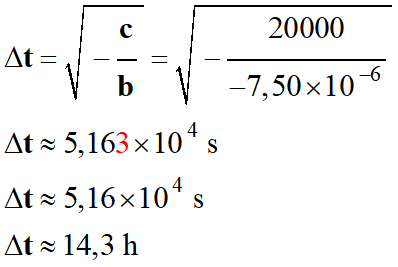
e)-
Hypothèses discutables :
-
La durée réelle de la chute est de 07h00.
-
La valeur trouvée par le calcul est plus du double
de la valeur réelle.
-
Le modèle utilisé ne convient pas.
-
Les différentes hypothèses qui ont permis le
calcul :
-
Philae est considéré en chute libre.
-
Le champ de pesanteur de la comète est considéré
comme uniforme, d'intensité moyenne :
-
g = 1,5 × 10–5
N . kg–1
-
Le référentiel de la comète est supposé galiléen.
-
Justification :
-
On considère que Philae est en chute libre,
-
Philae n’est soumis qu’à son poids.
-
On néglige toutes les autres forces.
-
Mais Philae peut être en interaction avec d’autres
systèmes (Soleil, ...)
-
Le champ de pesanteur est considéré comme uniforme.
-
Le mouvement s’effectue sur une distance de 20 km
environ.
-
Le champ de pesanteur varie avec l’altitude.
-
Le référentiel de la comète est supposé galiléen.
-
Le référentiel de la comète n’est pas galiléen.
-
Comme la durée du mouvement est de 7 h, pendant
cette durée la comète se déplace et son mouvement n’est pas rectiligne uniforme.
-
Lorsque l’on étudie la chute libre sur Terre :
-
On considère que le référentiel terrestre est
galiléen.
-
Ceci est vrai si l’expérience a une courte durée
(quelques secondes).
-
On peut considérer que le champ de gravitation est
uniforme dans une salle de classe.
-
On peut négliger les autres forces qui
interviennent si l’objet qui tombe est lourd et de faibles dimensions (bille).
-
Ainsi on peut négliger la poussée d’Archimède, les
forces de frottements (tant que la vitesse n’est pas trop grande)…

II-
Exercice :
Badminton, un sport dans le vent.
1)- Énoncé.
Le Badminton est un sport dans lequel on frappe un
volant, constitué de 2 parties :
-
une tête arrondie, qui
concentre une grande partie de la masse du volant ;
-
des
plumes, qui créent une traînée, modélisé par une force
 qui
s'oppose au mouvement du volant dans l’air.
qui
s'oppose au mouvement du volant dans l’air.
DONNÉES :
-
Masse de volant
m = 5,0 g
-
Intensité de la pesanteur terrestre : g
= 9,81 N . kg–1.
Volant de badminton

a)-
Indiquer le point (G1,
G2 ou
G3) sur le schéma
ci-dessus qui correspond au centre de masse du volant. Justifier la réponse.
b)-
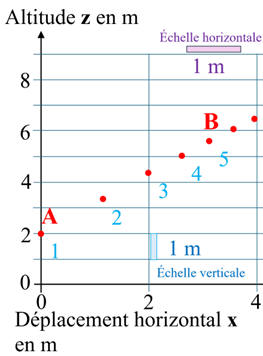
À l'aide d'une caméra un enregistrement du
mouvement du centre de masse du volant est réalisé lors d'un service. Le
résultat est donné ci-dessous.

-
L'intervalle de temps
entre deux points de mesure vaut Δt
= 50 ms.
-
Décrire, en première approximation, le mouvement du centre de masse du volant
sur la portion AB de sa trajectoire.
c)-
Sur cette partie
AB le poids
 du
volant est négligé devant la traînée
du
volant est négligé devant la traînée
 .
Exprimer puis calculer la norme de la force
.
Exprimer puis calculer la norme de la force
 .
.
d)-
Au-delà de la date
t = 6 s justifiez si le poids du
volant est toujours négligeable.
e)-
Le volant de badminton a été l'objet d’une
expérience réalisée par Thomas Pesquet à bord de la station spatiale
internationale en 2016.
Vidéo : Mouvement d'un volant de Badminton dans
ISS.
Vidéo

-
Décrire, dans le référentiel lié à l'ISS,
le mouvement du centre de masse du volant lorsqu'il est lâché par Thomas
Pesquet. En déduire la valeur de l'accélération
a du centre de masse du volant dans
ce référentiel.
f)-
Indiquer la ou les force(s) qui
s'applique(nt) sur le volant dans l'ISS.
En déduire si son mouvement observé dans la vidéo est cohérent avec la deuxième
loi de Newton. Déterminer alors si le référentiel de l'ISS
est galiléen.

2)- Correction.
a)-
Centre de masse du volant de badminton.
-
Schéma :

-
Pour des raisons de
symétrie suivant l’axe vertical et de lestage, le point
G3 correspond au centre de
masse du volant de badminton.
-
La tête concentre une
grande partie de la masse du volant (par rapport aux plumes).
-
Le
centre de masse du volant de badminton est plus proche du bas du volant.
b)-
Description du mouvement du centre de masse
du volant sur la portion AB de sa trajectoire :
-
Nature du mouvement :
-
Les points sont
sensiblement alignés
-
Le
mobile parcourt des distances de plus en petites pendant des durées égales.
-
Le
mobile est animé d’un mouvement rectiligne retardé (décéléré).
c)-
Expression et calcul la norme de la force
 :
:
-
Le système : le volant
de badminton :
-
Référentiel d’étude :
référentiel terrestre supposé galiléen
-
Bilan des forces :
-
Le
poids
 du
volant : direction verticale du lieu passant par le point
G3, orienté du haut vers
le bas.
du
volant : direction verticale du lieu passant par le point
G3, orienté du haut vers
le bas.
-
La traînée
 : direction
la droite AB, orienté dans le sens
inverse du mouvement du volant (orienté de
B vers
A).
: direction
la droite AB, orienté dans le sens
inverse du mouvement du volant (orienté de
B vers
A).
-
Sur
cette partie AB le poids
 du
volant est négligé devant la traînée
du
volant est négligé devant la traînée
 .
.
-
La deuxième loi de
Newton permet d’écrire la relation suivante :
-
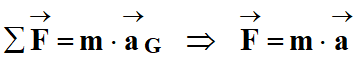
-
Caractéristiques du
vecteur accélération
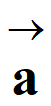 du centre de masse du bobsleigh :
du centre de masse du bobsleigh :
-
Le vecteur
accélération 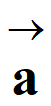 a même direction et même sens que le vecteur
a même direction et même sens que le vecteur
 .
.
-
Le mobile est animé
d’un mouvement rectiligne uniformément retardé.
-
Le vecteur
accélération
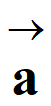 est un vecteur constant.
est un vecteur constant.
-
Expression de la
valeur de de la force  :
:
-
F
= m .
a
-
On
connaît la masse m
du volant : m
= 5,0 g
-
Il faut déterminer la
valeur de l’accélération a.
-
La seule méthode
possible est l’exploitation de l’enregistrement du mouvement du centre de masse
du volant sur le trajet rectiligne AB.
-
Il faut faire
attention au fait que l’échelle verticale est différente de l’échelle
horizontale.
-
Pour déterminer la
valeur de l’accélération, on utilise la formule approchée suivante :
-
Vecteur accélération
du centre de masse du système à la position 3 :
-
Le principe :
-
On utilise la notation
approchée suivante :
-
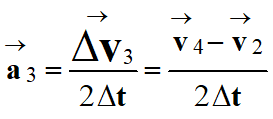
-
Le vecteur vitesse :
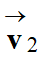
-
Relation approchée :
-
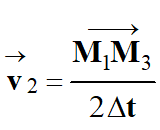
-
Le point d’application
est le point M2, sa
direction la droite (AB) et sa
valeur :
-
On peut travailler
avec les coordonnées :
-
Coordonnées du point
M1 (x1
= 0,0 m ; y1 = 2,0 m)
-
Les
différentes mesures pour le point M3
(avec Word)
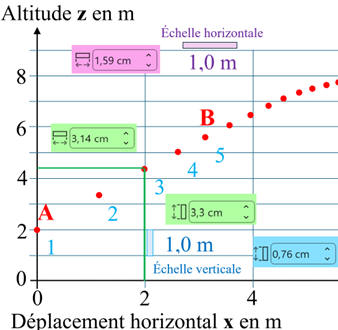
-
Étude du segment
M1M3 :
-
Abscisse du point
M3
|
Graphique
|
Réel
|
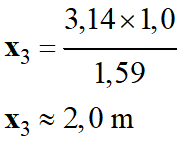
|
|
1,59 cm
|
1,0 m
|
|
3,14 cm
|
x3
|
-
Ordonnée du point
M3 :
|
Graphique
|
Réel
|
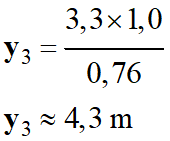
|
|
0,76 cm
|
1,0 m
|
|
3,3 cm
|
y3
|
-
Coordonnées du point
M3 (x3
≈ 2,0 m ; y3 ≈ 4,3 m)
-
Coordonnées du segment
M1M3 :
|
|
M1M3
|
|
Abscisse
|
x3
– x1
|
=
|
2,0 m
|
|
Ordonnée
|
y3
– y1
|
=
|
2,3 m
|
-
Longueur du segment
M1M3 :
-
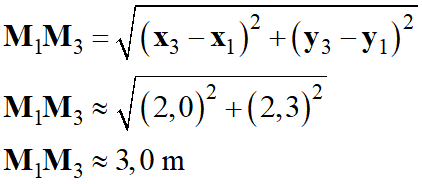
-
On peut en déduire la
valeur de la vitesse v2 :
-
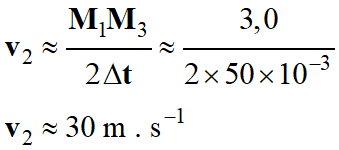
-
Le vecteur vitesse :
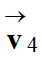
-
Relation approchée :
-
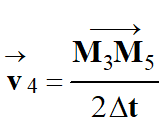
-
Le point d’application
est le point M4, sa
direction la droite (AB) et sa
valeur :
-
On peut travailler
avec les coordonnées :
-
Les
différentes mesures pour le point M5
(avec Word)
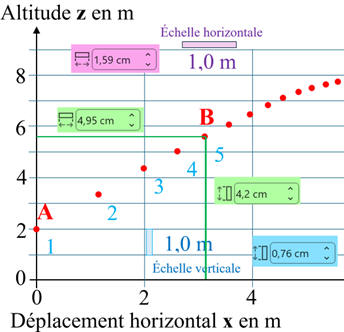
-
Étude du segment
M3M5 :
-
Abscisse du point
M5
|
Graphique
|
Réel
|
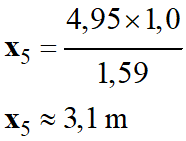
|
|
1,59 cm
|
1,0 m
|
|
4,95 cm
|
x5
|
-
Ordonnée du point
M5 :
|
Graphique
|
Réel
|
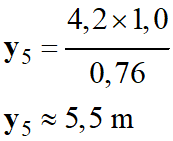
|
|
0,76 cm
|
1,0 m
|
|
4,2 cm
|
y5
|
-
Coordonnées du point
M5 (x5
≈ 3,1 m ; y3 ≈ 5,5 m)
-
Coordonnées du point
M3 (x3
≈ 2,0 m ; y3 ≈ 4,3 m)
-
Coordonnées du segment
M3M5 :
|
|
M3M5
|
|
Abscisse
|
x5
– x3
|
=
|
1,1 m
|
|
Ordonnée
|
y5
– y3
|
=
|
1,2 m
|
-
Longueur du segment
M3M5 :
-
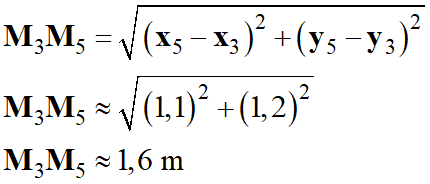
-
On peut en déduire la
valeur de la vitesse v5 :
-
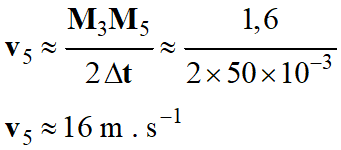
-
Détermination du
vecteur accélération
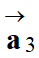
-
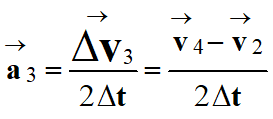
-
Or les
vecteurs vitesses
et
ont
même direction, la droite (AB) :
-
La valeur de
l’accélération a3 se calcule à partir de la relation suivante :
-
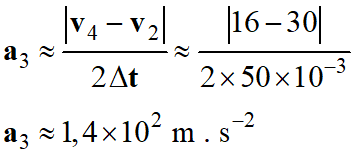
-
On peut faire une
représentation graphique du vecteur variation de vitesse
-
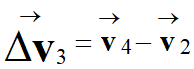
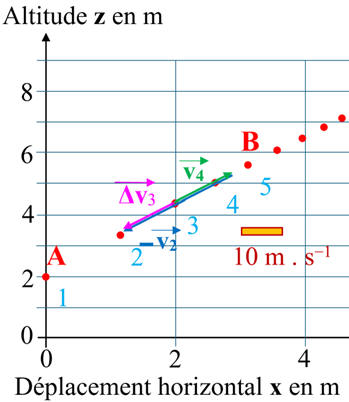
ZOOM
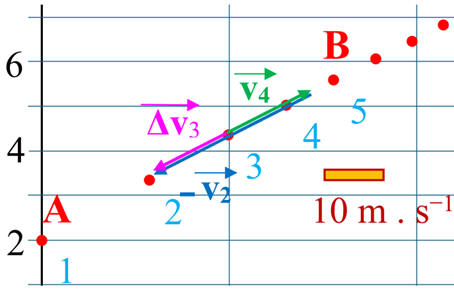
-
La longueur du
représentant du vecteur :
-
ℓΔv3 ≈
1,4 cm
-
En conséquence :
Δv3 = 14 m . s-1
-
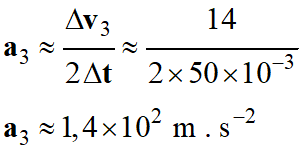
►
Valeur de la force de
traînée :
-
F
= m .
a avec a =
a3 et m = 5,0
g
-
F
≈ 5,0 × 10-3 × 1,4 × 102
-
F
≈ 0,70 N
d)-
Au-delà de la date
t = 6 s justification si le poids
 du
volant est toujours négligeable.
du
volant est toujours négligeable.
-
Nature du mouvement :
-
À partir de la date
t = 6 s, le mouvement n’est plus rectiligne, il devient curviligne.
-
Il découle de ceci que
le vecteur accélération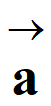 change de direction et de valeur.
change de direction et de valeur.
-
On ne
peut plus négliger le poids
 du
volant devant la force de traînée
du
volant devant la force de traînée
 .
.
-
La deuxième loi de
Newton permet d’écrire la relation suivante :
-
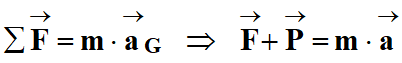
-
Le
vecteur accélération
 a même direction et même sens que le vecteur somme
vectorielle des forces
a même direction et même sens que le vecteur somme
vectorielle des forces
 et
et
 .
.
-
La force
 de traînée
d’un volant de badminton dépend de sa vitesse, de la densité de l’air, de sa
forme et du coefficient de traînée.
de traînée
d’un volant de badminton dépend de sa vitesse, de la densité de l’air, de sa
forme et du coefficient de traînée.
-
La force
 de traînée
dépend essentiellement de la vitesse du volant.
de traînée
dépend essentiellement de la vitesse du volant.
-
On remarque qu’au
cours du mouvement, la vitesse du volant diminue (la distance entre les
différents points diminue au cours du temps).
-
Comme
la force de traînée diminue, le poids du volant n’est plus négligeable et influe
de plus en plus sur le mouvement du volant.
e)-
Mouvement du centre de masse du volant
lorsqu'il est lâché par Thomas Pesquet.
-
Le
centre de masse du volant lâché par Thomas Pesquet dans l'ISS se déplace en
ligne droite à vitesse constante (la vitesse donnée au départ) dans le
référentiel lié à l'ISS.

Vidéo
f)-
Force(s) qui s'applique(nt) sur le volant
dans l'ISS.
-
La
principale force agissant sur l’ISS
est la force gravitationnelle d’attraction de la Terre.
-
Il en va de même pour
le volant :
-
Il est soumis à la
force gravitationnelle :
-
Schéma :
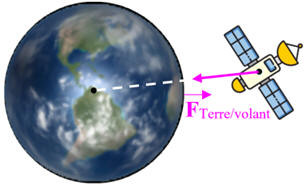
-
Le mouvement du volant
dans l’ISS est rectiligne uniforme ce
qui n’est pas cohérent avec la deuxième loi de Newton.
-
L’ISS
suit une orbite circulaire stable autour de la Terre.
-
L’ISS
est animé d’un mouvement circulaire uniforme dans le référentiel géocentrique
lié à la Terre.
-
Le référentiel de l'ISS n’est pas galiléen
-
L’ISS
utilise des systèmes de propulsion pour ajuster son orbite et sa position.
-
Ces ajustements sont
soigneusement planifiés pour minimiser les perturbations et maintenir un
mouvement uniforme.
-
L’ISS
(station spatiale internationale) tourne autour de la Terre à une vitesse
constante de 27600 km . h-1.
-
Les forces
gravitationnelles et la vitesse orbitale sont équilibrées, ce qui maintient les
objets en mouvement sur une trajectoire rectiligne uniforme.

III- Exercice :
Bobsleigh.
1)- Énoncé.
Le bobsleigh est un sport d'hiver dans
lequel des équipes de 2 ou 4 personnes effectuent des courses dans un traîneau
appelé bobsleigh, sur des pistes de glace étroites.

DOC. 1 Premières phases de la course
-
Phase 1 :
l'équipage pousse le bobsleigh vide avec une force constante sur une piste
rectiligne horizontale longue de d1 = 50 m,
sans frottement. La valeur de la vitesse de l'engin
passe de 0 à 45 km . h-1 en une durée de Δt1 = 6,0
s.
-
Phase 2 :
l'équipage saute dans le bobsleigh qui parcourt alors une distance d1
= 10 m sur une partie rectiligne horizontale sans frottement.
-
Phase 3 :
le système {bobsleigh ; équipage} se déplace sur une partie rectiligne inclinée
vers le bas d'un angle α = 15°, sans frottement, pendant une durée Δt3
= 7,0 s.
-
Phase 4 :
le système {bobsleigh ; équipage} se déplace sur une piste courbe inscrite dans
un plan horizontal au Oxy (voir DOC. 2).
DOC. 2 :
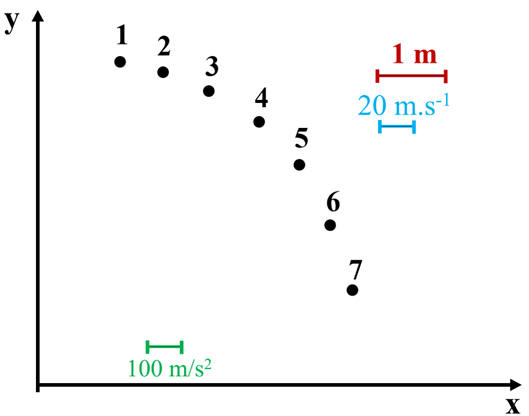
-
La position 1 correspond à la première
position du système lors de la phase 4.
-
La durée entre 2
positions successives est Δt =30 ms.
DONNÉES :
-
Intensité de la pesanteur : g =
9,81 N . kg–1
-
Masse du bobsleigh : m = 200 kg
-
Masse du bobsleigh avec
équipage : M = 500 kg
Questions :
1.
Indiquer un justifiant la réponse le type de
mouvement du centre de masse du système {bobsleigh} lors de la phase 1. En
déduire les caractéristiques du vecteur accélération du centre de masse du
bobsleigh.
2.
Exprimer la norme de la force
 appliquée par les équipiers au bobsleigh lors de la phase 1.
appliquée par les équipiers au bobsleigh lors de la phase 1.
3.
Indiquer en justifiant le type de mouvement du
centre de masse du système { bobsleigh ; équipage} dans la phase 2. En déduire
la valeur de sa vitesse à la fin de la phase 2.
4.
Faire un schéma représentant le bilan des
forces appliquées au système { bobsleigh ; équipage} lors de la phase 3. En
déduire la valeur de l'accélération du centre de masse du système durant cette
phase et la valeur de sa vitesse à la fin de cette phase.
5.
Recopier le schéma du
DOC. 2 et représenter le
vecteur accélération du centre de masse du système {bobsleigh ; équipage} à la
position 4 de la phase 4, en laissant les étapes de construction de ce vecteur
apparentes. Déterminer la norme de ce vecteur.

2)- Correction.
1.
Type de mouvement du centre de masse du système
{bobsleigh} lors de la phase 1.
-
Phase 1 :
l'équipage pousse le bobsleigh vide avec une force constante sur une piste
rectiligne horizontale longue de d1
= 50 m, sans frottement. La valeur de la vitesse de l'engin passe de 0 à 45 km
. h–1 en une durée de Δt1
= 6,0 s.
-
La piste est rectiligne horizontale,
-
Les frottements sont négligeables :
-
Référentiel d’étude : référentiel lié à
la piste (référentiel terrestre supposé galiléen)
-
Bilan des forces :
-
Force appliquée
 par les équipiers au
bobsleigh lors de la phase 1 (force constante sur une piste rectiligne).
par les équipiers au
bobsleigh lors de la phase 1 (force constante sur une piste rectiligne).
-
Poids
 du bobsleigh, force verticale
orientée du haut vers le bas
du bobsleigh, force verticale
orientée du haut vers le bas
-
La réaction
 du support, force verticale
orientée du bas vers le haut
du support, force verticale
orientée du bas vers le haut
-
avec

-
Schéma de la situation :
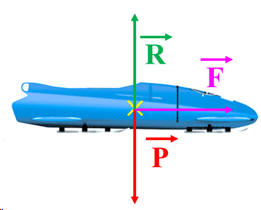
-
Deuxième loi de Newton.
-
Énoncé :
|
Dans un référentiel galiléen,
la somme des
vecteurs forces
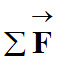 appliquées à un
système S, appliquées à un
système S,
de masse m et de centre de
masse G,
est égal au produit de sa masse m
par le vecteur accélération 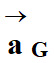 de son centre de masse.
de son centre de masse.
|
|
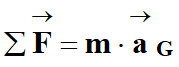
|
Valeur des forces F en newton
(N)
|
|
Valeur de la masse m en
kilogramme (kg)
|
|
Valeur de l’accélération aG
en mètre par seconde au carré (m . s–2)
|
-
Dans le cas présent :
-
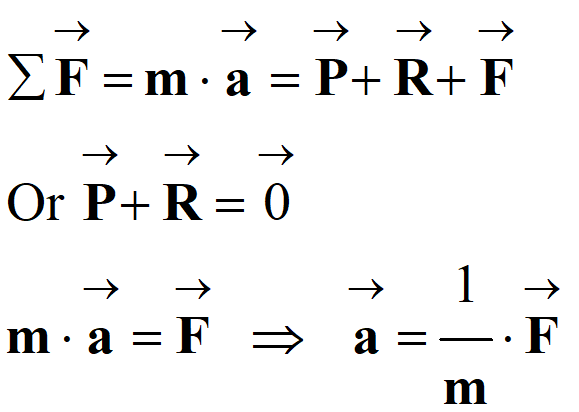
-
Caractéristiques du vecteur
accélération du centre de masse du bobsleigh :
-
Le vecteur accélération
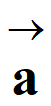 a même
direction et même sens que le vecteur
force
a même
direction et même sens que le vecteur
force
 .
.
-
Le mobile est animé d’un mouvement
rectiligne uniformément accéléré.
-
Le vecteur accélération
est un vecteur constant.
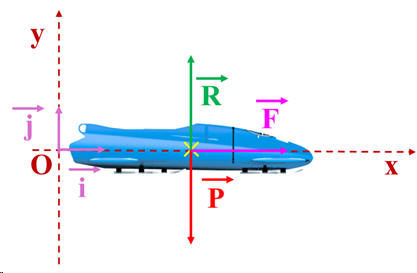
-
Coordonnées du vecteur
accélération dans le repère
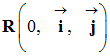
-
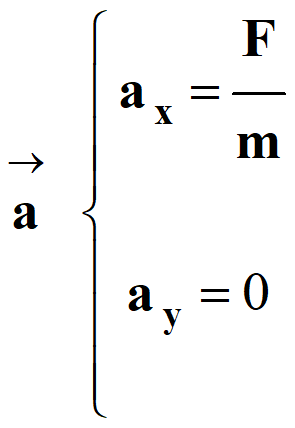
-
Conditions initiales :
-
Vecteur position :
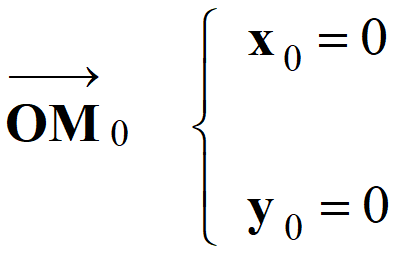 et vecteur vitesse initiale :
et vecteur vitesse initiale :
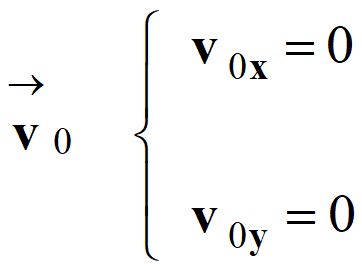
-
D’autre part :
-
Piste rectiligne
horizontale longue de d1
= 50 m,
-
La valeur de la vitesse
de l'engin passe de 0 à 45 km . h–1 en une durée de
Δt1
= 6,0 s.
-
Or par définition :
-
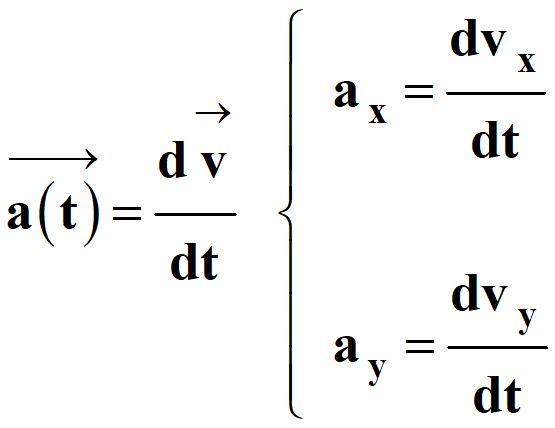
-
La coordonnée
vx
est une primitive de ax :
-
La primitive est connue à une constante
près.
-
Cette constante que l'on
note vox
est liée aux conditions initiales.
-
Elle représente la
composante de la vitesse du mobile suivant l'axe
x'Ox au temps
t
= 0.
-
En conséquence, les constantes qui
apparaissent sont liées aux conditions initiales et parfaitement connues à
partir des conditions initiales
-
Comme :
-
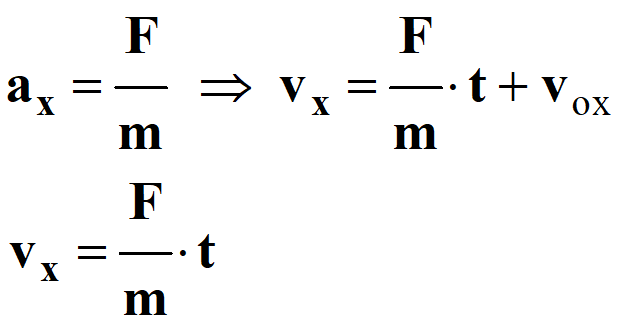
-
De même :
ay =
0, alors vy
= cte = v0y
= 0
-
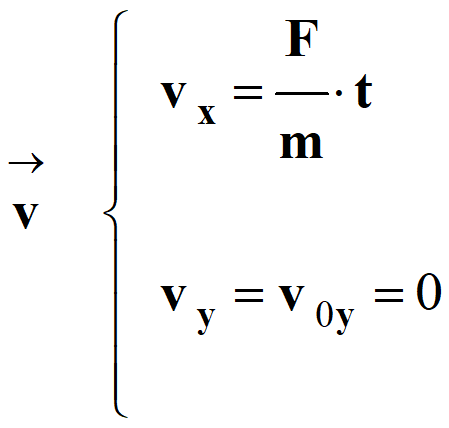
-
Au temps
t1
= 6,0 s :
-
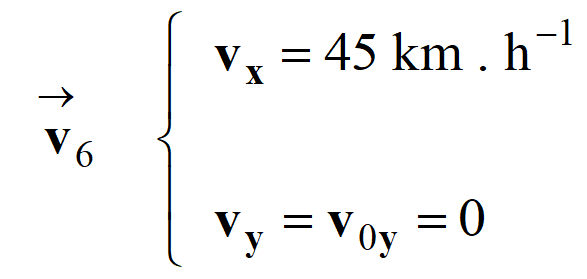
-
On en déduit que :
-
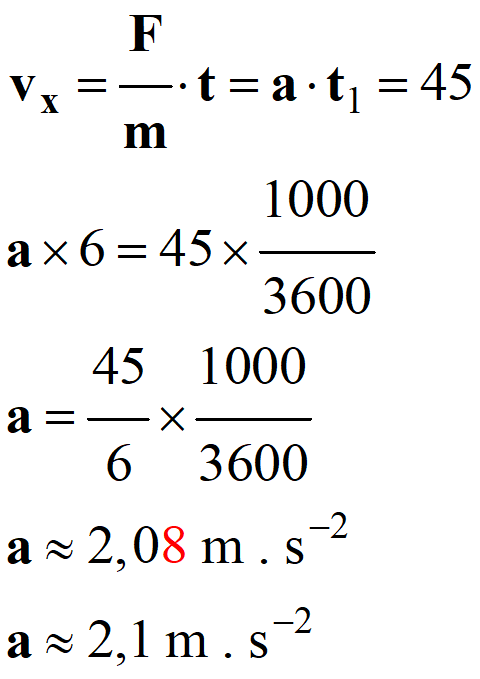
-
Le vecteur accélération
est horizontal, orienté dans le sens du mouvement et de nome : a ≈ 2,1 m . s–2.
- 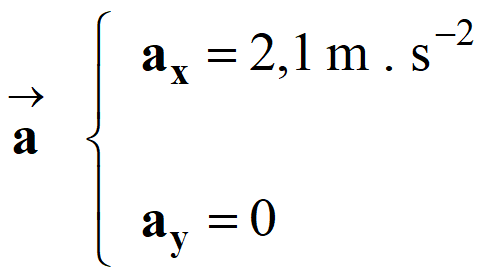
2. Norme de la force appliquée par les équipiers
au bobsleigh lors de la phase 1.
- 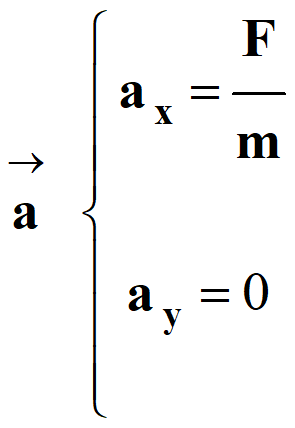 avec
avec 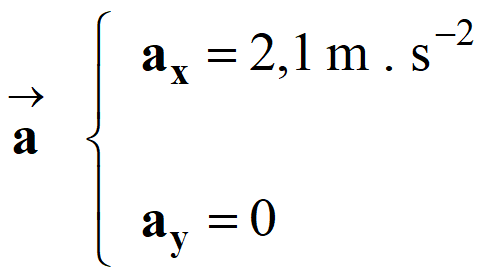
- 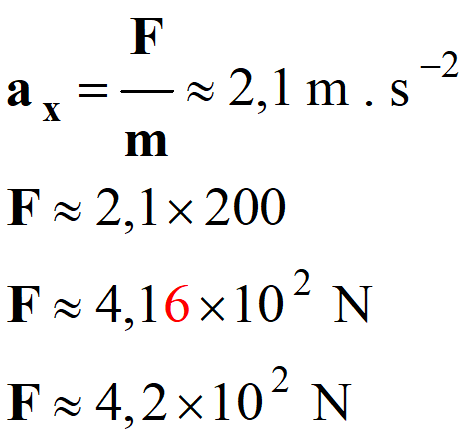
- Le vecteur force  est horizontal,
orienté dans le sens du mouvement et de nome :
est horizontal,
orienté dans le sens du mouvement et de nome :
- F ≈ 4,2
× 102 N.
3. Type de mouvement du centre de masse du
système {bobsleigh ; équipage} dans la phase 2.
- Phase 2 :
l'équipage saute dans le bobsleigh qui parcourt alors une distance d1
= 10 m sur une partie rectiligne horizontale sans frottement.
- La piste est rectiligne horizontale,
- Les frottements sont négligeables :
- Référentiel d’étude : référentiel lié à
la piste (référentiel terrestre supposé galiléen)
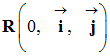
- Bilan des forces :
- Poids
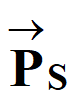 du
système {bobsleigh ; équipage, force verticale
orientée du haut vers le bas
du
système {bobsleigh ; équipage, force verticale
orientée du haut vers le bas
- La réaction du support
 , force verticale
orientée du bas vers le haut
, force verticale
orientée du bas vers le haut
- avec 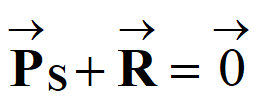
- Schéma de la situation :
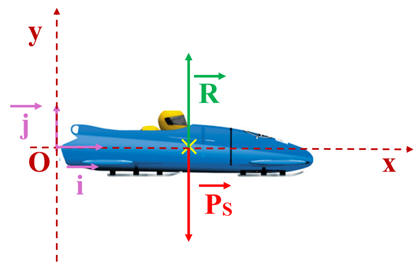
- Deuxième loi de Newton :
- 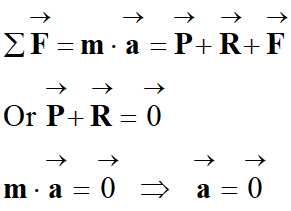
- Le vecteur accélération est un vecteur
nul.
- Conditions initiales de la phase 2 :
- 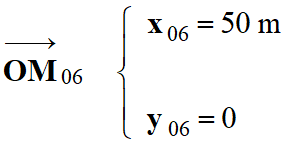 et vecteur vitesse initiale :
et vecteur vitesse initiale :
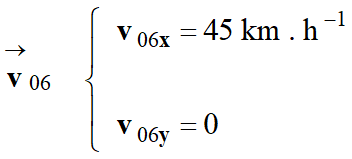
- Le système est animé
d’un mouvement rectiligne uniforme de vitesse v
= 45 km . h–1
- La vitesse à la fin de
la phase 2 : v
= 45 km . h–1
4. Schéma représentant le bilan des forces
appliquées au système {bobsleigh ; équipage} lors de la phase 3.
- Phase 3 :
le système {bobsleigh ; équipage} se déplace sur une partie rectiligne inclinée
vers le bas d'un angle α
= 15°, sans frottement, pendant une durée Δt3
= 7,0 s.
- Bilan des forces lors de la phase 3 :
- Poids
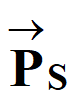 du système S
= {bobsleigh ; équipage}, force verticale orientée du haut vers le bas
du système S
= {bobsleigh ; équipage}, force verticale orientée du haut vers le bas
- La réaction du support
 , perpendiculaire
au support, orientée du bas vers le haut (les frottements sont nuls)
, perpendiculaire
au support, orientée du bas vers le haut (les frottements sont nuls)
- avec
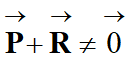
- Schéma de la situation :
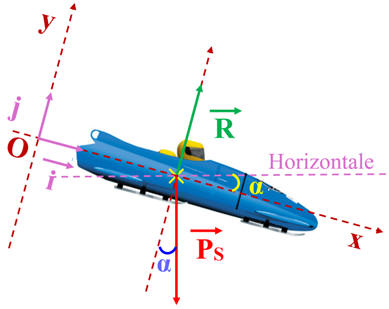
- Coordonnées des différents vecteurs
dans le repère
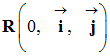
- Vecteur poids :
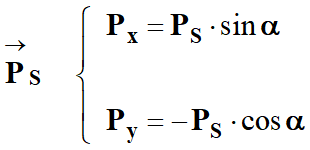
- Le vecteur
réaction du support :
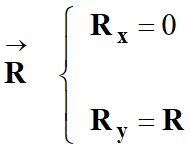
- Deuxième loi de Newton :
- 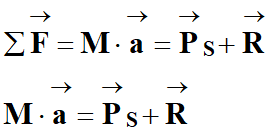
- On en déduit les expressions
suivantes :
- 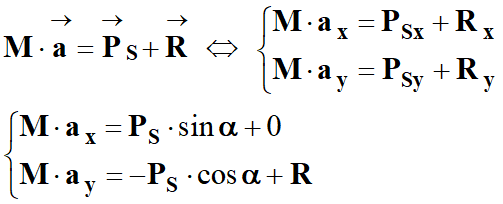
- La projection sur l’axe
Ox :
M . ax =
PS
sin α
- La projection sur l’axe
Oy :
M . ay = -
PS
cos α + R = 0
- Il n’y a pas de
mouvement sur l’axe Oy.
- Coordonnées du vecteur accélération :
- 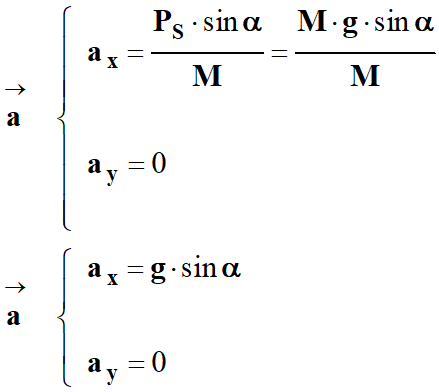
- la valeur de l'accélération du centre
de masse du système durant la phase 3.
- a
= ax
= g
. sin α
- a
= ax
= 9,81 . sin 15
- a
= ax
≈ 2,53 m . s–2
- Valeur de la vitesse à la fin de la
phase 3.
- La durée de la phase 3 :
Δt3
= 7,0 s.
- La vitesse à la fin de
la phase 2 : v
= 45 km . h–1
- C’est la vitesse initiale de la phase
3.
- Notation :
- v03
= 45 km . h–1
- 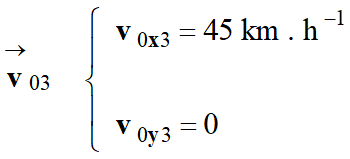
- En partant du vecteur accélération :
- 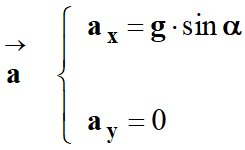
- La coordonnée vx
est une primitive de ax :
- La primitive est connue à une constante
près.
- Cette constante que l'on
note vox3
est liée aux conditions initiales.
- Elle représente la
composante de la vitesse du mobile suivant l'axe x'Ox au temps
t = 0 pour la phase 3.
- En conséquence, les constantes qui
apparaissent sont liées aux conditions initiales et parfaitement connues à
partir des conditions initiales
- Comme :
- 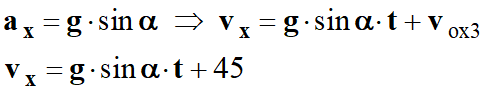
- 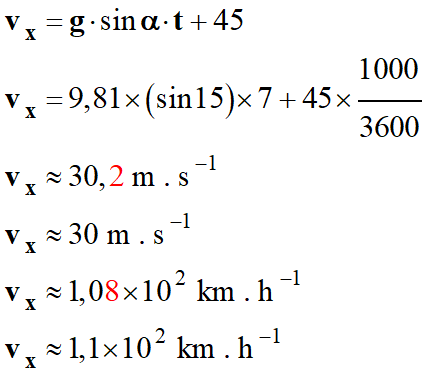
- Environ 110 km . h–1.
5.
Représentation du vecteur
accélération du centre de masse du système {bobsleigh ; équipage} à la position
4 de la phase 4 :
-
Le principe :
-
On utilise la notation approchée
suivante :
-
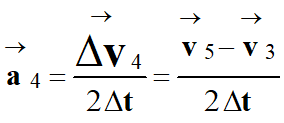
-
Le vecteur vitesse :
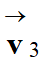
-
Relation approchée :
- 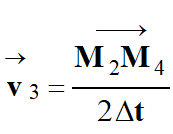
-
Le point d’application est le
point M3, sa direction la
droite (M2M4) et sa valeur :
-
Avec l’échelle donnée :
-
M2M4
≈ 1,6 m
-
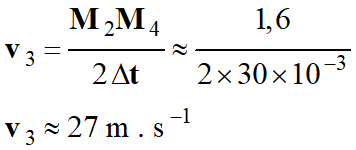
-
Longueur du représentant avec
l’échelle choisie :
-
ℓv3 ≈ 1,3 cm
-
Puis pour le vecteur
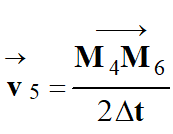
-
M4M6
≈ 1,8 m
- 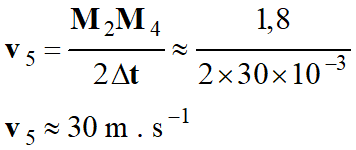
-
Longueur du représentant avec
l’échelle choisie :
-
ℓv5 ≈ 1,5 cm
-
Le tracé :
-
À partir du point
M4, on trave le représentant du vecteur
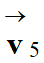 (direction droite
M4M6)
(direction droite
M4M6)
-
À l’extrémité de ce vecteur, on
trace le vecteur
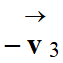 (direction parallèle à la droite
M2M4)
(direction parallèle à la droite
M2M4)
-
On trace le vecteur
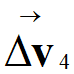 ,
dont l’origine
est le point M4 et
l’extrémité celle du vecteur
,
dont l’origine
est le point M4 et
l’extrémité celle du vecteur
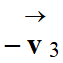 .
.
-
La mesure du représentant du
vecteur donne :
-
ℓΔv4 ≈ 0,72 cm
-
Avec l’échelle utilisée :
-
Δv4 ≈ 14 m . s–1
-
Valeur de l’accélération au point
M4 :
-
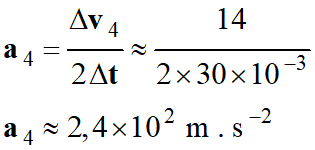
-
ℓa4 ≈
2,4 cm
-
Représentation graphique :


IV- Exercice :
Décollage d’Ariane 5 .
1)- Énoncé.
La propulsion de la fusée Ariane 5 est assurée par :
-
Un étage principal cryotechnique
(EPC) constitué notamment d'un moteur vulcain ;
-
Deux boosters (étage
d'accélération à poudre EAP) qui contribue à environ 90% de la puissance totale
transmise à la fusée au début du décollage.
Le but de cet exercice est de vérifier certaines des caractéristiques de la
fusée Ariane 5 en étudiant son décollage.
La masse totale de la fusée est supposée constante pendant la durée de
l'étude.
►
La fusée Ariane 5 :

https://fr.wikipedia.org/wiki/Ariane_5
DONNÉES :
-
Intensité de la pesanteur :
g = 9,81 N . kg–1
-
Masse d’Ariane 5 au décollage :
M = 750 à 780 t
-
Norme de la force de poussée de la
fusée au décollage : 12000 à 13000 kN.
DOC. 1 Début du décollage
d’Ariane 5.
L'axe vertical a pour origine la base de la fusée au moment du décollage.
L'image 1 précise l'endroit de la fusée qui sert à repérer son mouvement
vertical.
Son ordonnée sur l'axe Oy est notée y1.

Figure .2 : Chronophotographie du décollage d'Ariane 5
DOC. 2 Détermination
expérimentale de la position et de la valeur de la vitesse de la fusée
|
Image
|
Date t
(en s)
|
Position y
(en m)
|
Valeur de
la
vitesse
verticale vy
(en m . s–1)
|
|
1
|
0,20
|
30,1
|
–
|
|
2
|
0,60
|
31,5
|
vy2
|
|
3
|
1,00
|
33,3
|
6,8
|
|
4
|
1,40
|
36,9
|
9,6
|
|
5
|
1,80
|
y5
|
12
|
|
6
|
2,20
|
46,5
|
15
|
|
7
|
2,60
|
52,9
|
–
|
DOC. 3 Évolution de la
valeur de la vitesse verticale de la fusée en fonction du temps

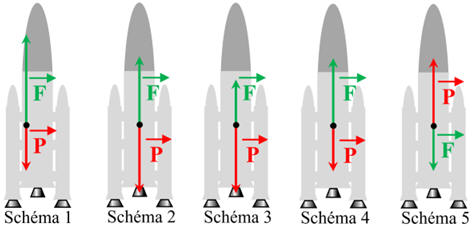
DOC. 4 Proposition de
représentation des forces s'appliquant sur la fusée qui vient de quitter le sol
1.
Questions préliminaires.
a)-
Estimer, à l’aide des
DOC.1
et 2,
les valeurs de y5 et de vy2,
en détaillant la démarche utilisée et en vérifiant la cohérence du résultat
obtenu pour vy2
à l’aide du
DOC. 3.
b)-
Choisir parmi les propositions du
DOC. 4 le schéma compatible
avec le décollage de la fusée. Justifier qualitativement la réponse.
2.
Problème
►
À l'aide des documents, des réponses précédentes et de connaissances,
estimer la norme de la force de poussée au décollage
et
vérifier la cohérence de ce résultat avec les DONNÉES.

2)- Correction.
1.
Questions préliminaires.
a)-
Estimation des valeurs de y5 et de vy2.
-
Détermination de la valeur de y5
à partir du DOC. 1 :
-
Mesures effectuées avec le traitement de texte Word :

|
Graphique
|
Réel
|
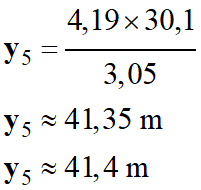
|
|
3,07 cm
|
y1
= 30,1m
|
|
4,19 cm
|
y5
|
-
Détermination de la valeur de vy2
à partir du DOC. 2 :
-
Pour pouvoir atteindre la valeur de la vitesse à
l’instant t2, on calcule la vitesse moyenne pendant un
intervalle de temps très court encadrant l’instant considéré :
-
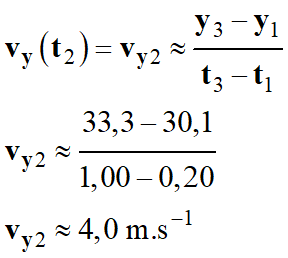
-
Ce résultat est en accord avec celui du graphique
(DOC. 3)

b)-
Schéma compatible avec le décollage de la fusée.
-
Schéma compatible : Schéma 4

-
Pour que la fusée s’élève verticalement vers le
haut :
-
La valeur de la force
 de
poussée doit être supérieure à celle du poids
de
poussée doit être supérieure à celle du poids
 .
.
-
La direction des forces doit être confondue avec
l’axe de symétrie de la fusée.
2.
Problème
►
À l'aide des documents, des réponses précédentes et
de connaissances, estimer la norme de la force de poussée au décollage
et
vérifier la cohérence de ce résultat avec les DONNÉES.
DONNÉES :
-
Intensité de la pesanteur : g = 9,81 N . kg–1
-
Masse d’Ariane 5 au décollage : M = 750 à
780 t
-
Norme de la force de poussée de la fusée au
décollage : 12000 à 13000 kN
-
De plus :
-
La masse totale de la fusée est supposée constante
pendant la durée de l'étude.
-
Force de poussée au décollage :

►
Approche du problème
:
-
Référentiel d’étude : repère terrestre
supposé galiléen (lié au sol) :
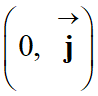
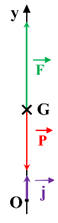
-
Bilan des forces :
-
Le poids
 de
la fusée : direction verticale du lieu passant par le point G,
centre de masses et orienté du haut vers le bas.
de
la fusée : direction verticale du lieu passant par le point G,
centre de masses et orienté du haut vers le bas.
-
La poussée
 :
direction verticale passant par le point G , orienté du bas vers le haut.
:
direction verticale passant par le point G , orienté du bas vers le haut.
-
Coordonnées des vecteurs :
-
 (Py = - P = - M . g)
(Py = - P = - M . g)
-
 (
Fy = F)
(
Fy = F)
- Deuxième loi de Newton :
|
Dans un référentiel galiléen, la
somme des vecteurs forces 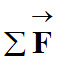
appliquées à un
système S, de masse m et de centre de masse G,
est égal au
produit de sa masse m par le vecteur accélération
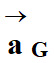
de son centre de
masse.
|
|
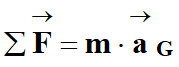
|
Valeur des
forces F en newton (N)
|
|
Valeur de la
masse m en kilogramme (kg)
|
|
Valeur de
l’accélération aG en mètre par
seconde au carré
(m . s–2)
|
-
Référentiel d’étude : Référentiel de la comète supposé galiléen
-
Repère lié au référentiel :
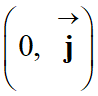
-
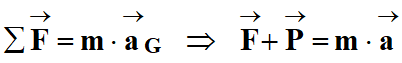
-
On tire de cette relation :
-
Fy +
Py =
M .
ay
-
F
-
Py=
M . ay
-
F
-
M .
g = M .
ay
-
F =
M . (g + ay)
-
Remarque :
-
Coordonnée du vecteur accélération 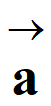 : ( ay =
a)
: ( ay =
a)
-
Comme F >
P, et que les vecteurs
 et
et
 ont la même direction (verticale passant par
G)
ont la même direction (verticale passant par
G)
-
Le vecteur accélération est vertical et orienté du bas vers le haut.
►
Relation qui permet de calculer la force de poussée :
-
F =
M . (g
+ a)
-
Les grandeurs M et
g sont connues.
-
Il faut calculer la valeur de l’accélération
a.
-
Il faut déterminer la valeur de l’accélération
a.
-
La seule méthode possible est l’exploitation du
DOC. 2
|
Image
|
Date t
(en s)
|
Position y
(en m)
|
Valeur de
la vitesse
verticale vy
(en m . s–1)
|
|
1
|
0,20
|
30,1
|
–
|
|
2
|
0,60
|
31,5
|
4,0
|
|
3
|
1,00
|
33,3
|
6,8
|
|
4
|
1,40
|
36,9
|
9,6
|
|
5
|
1,80
|
41,4
|
12
|
|
6
|
2,20
|
46,5
|
15
|
|
7
|
2,60
|
52,9
|
–
|
-
On peut calculer la valeur de l’accélération en utilisant la relation suivante :
-
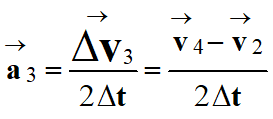
-
En utilisant la coordonnée des vecteurs :
-
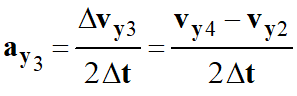 Avec
Δt = 0,40 s
Avec
Δt = 0,40 s
|
Image
|
t
(en s)
|
y
(en m)
|
vy
(m / s)
|
ay
(m / s2)
|
|
|
0,00
|
0,0
|
|
|
|
1
|
0,20
|
30,1
|
|
|
|
2
|
0,60
|
31,5
|
4,00
|
|
|
3
|
1,00
|
33,3
|
6,8
|
7,0
|
|
4
|
1,40
|
36,9
|
9,6
|
6,5
|
|
5
|
1,80
|
41,4
|
12
|
6,8
|
|
6
|
2,20
|
46,5
|
15
|
|
|
7
|
2,60
|
52,9
|
|
|
-
Ainsi on peut estimer la force de poussée au démarrage de la fusée.
-
ay3
≈ 7,0 m . s-2
-
Estimation de la valeur de la poussée F au
démarrage :
-
F =
M . (g + a)
-
F =
M . (g + a)
-
F ≈ 750 × 103 × (9,81 +
7,0)
-
F ≈ 1,26
× 107 N
-
F ≈ 1,3 × 107 N
-
Norme de la force de poussée de la fusée au décollage : 12000 à 13000 kN.
-
Le résultat est bien en accord avec la donnée de l’énoncé.
►
Autre approche pour connaître la valeur de l’accélération.
-
On peut utiliser les données liées à la vitesse lors du démarrage.
-
On exploite le DOC. 3.
-
On trace la courbe de tendance avec le tableur Excel :
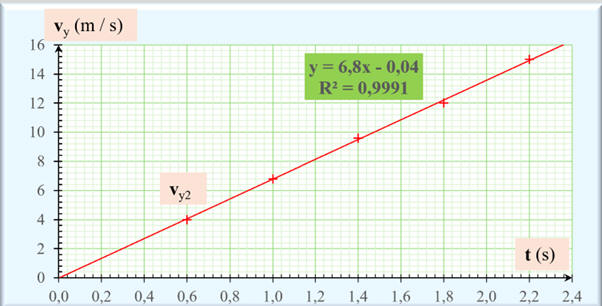
-
Traduction physique :
-
Relation mathématique : y ≈ 6,8
x
-
Relation en physique : vy ≈ 6,8 t
-
Le coefficient de détermination R2
est proche de 1.
-
Les deux grandeurs sont en adéquation.
-
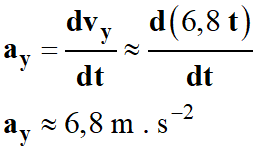
-
Ce résultat est en accord avec celui trouvé précédemment.
-
Estimation de la valeur de la poussée F au
démarrage :
-
F =
M . (g + a)
-
F =
M . (g + a)
-
F ≈ 750 × 103 × (9,81 +
6,8)
-
F ≈ 1,24
× 107 N
-
F ≈ 1,2 × 107 N
-
Norme de la force de poussée de la fusée au décollage : 12000 à 13000 kN.
-
Le résultat est bien en accord avec la donnée de l’énoncé.
►
Autre méthode :
-
On peut utiliser le théorème de l’énergie cinétique.
-
Énoncé :
|
-
La variation de l’énergie cinétique d’un système
S
en mouvement,
d’une position
A à une position
B,
est égale à la somme des
travaux de toutes les forces appliquées au
système
S
entre A
et B :
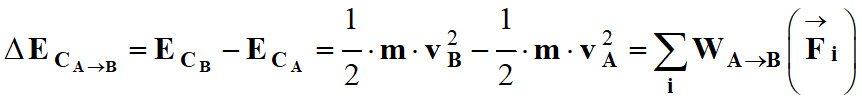
|
-
Les unités :
|
ΔECA→B
|
Variation de l’énergie cinétique en joule (J)
|
|
ECA et ECB
|
Énergie cinétique en joule (J)
|
|
m
|
La masse en
kilogramme (kg)
|
|
v
|
La vitesse en
mètre par seconde (m . s–1)
|
|
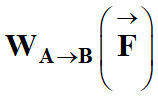
|
Travail de la force
en joule (J)
|
|
F
|
Valeur de la
force en newton (N)
|
|
AB
|
Longueur du
déplacement en mètre (m)
|
|
cos α
|
α
angle (rad ou °) entre les vecteurs
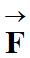 et et
cos
α
: sans unité
|
-
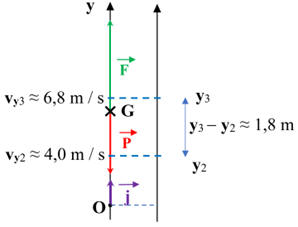
Repère d’étude :
-
Le théorème de l’énergie cinétique appliqué à la fusée entre les instants
t2 et
t3 permet d’écrire la
relation suivante :
-
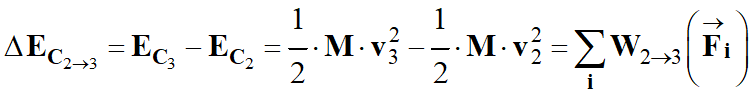
-
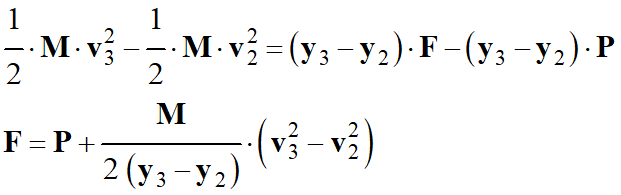
-
En utilisant les données :
-
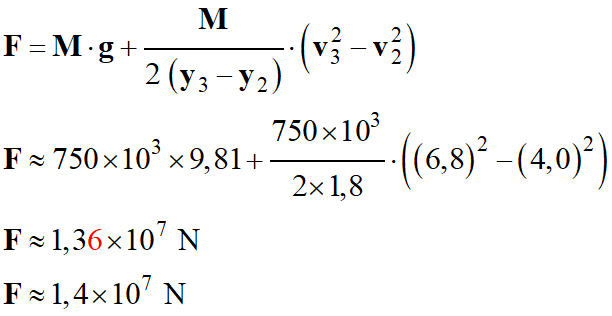
-
L’ordre de grandeur de cette poussée est en accord avec l’estimation donnée dans
l’énoncé.
Mise en orbite d'un satellite artificiel par la
fusée Ariane
Décollage de la fusée Ariane 5

V- Exercice : .
1)- Énoncé.
Une bille de masse constante, modélisée
par un point matériel, est lâchée verticalement dans un tube dans lequel on a
fait le vide.
Un chronomètre est déclenché au moment du lâcher.
Les normes des vecteurs position, vitesse et
accélération de cette bille sont représentées ci-dessous.
L'axe vertical
Oy est orienté vers le bas, son origine étant
confondue avec la position du point matériel à l'instant du lâcher.
Le mouvement étudié est rectiligne uniformément
accéléré.
Courbe 1 :
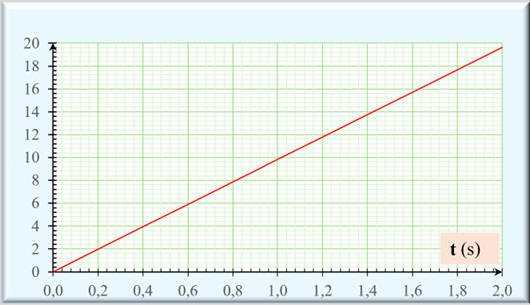
Courbe 2 :
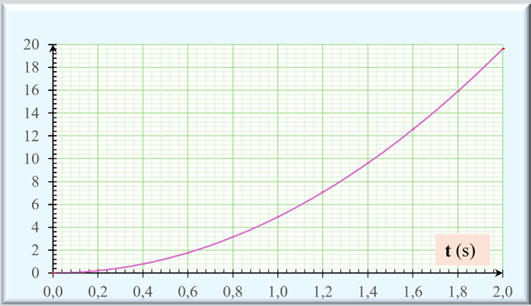
Courbe 3 :
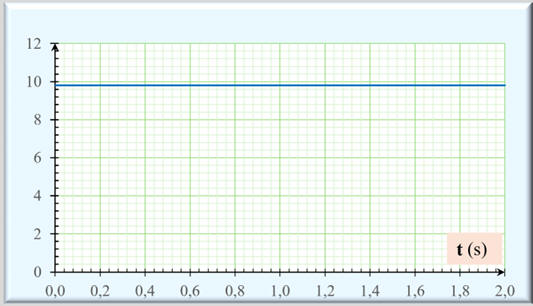
►
Après avoir identifié les courbes ci-dessus, montrer que la bille est
soumise à une force constante.

2)- Correction.
-
Le mouvement
étudié est rectiligne uniformément accéléré.
-
Étude du système
-
Système
S : la bille
-
Conditions initiales :
-
Vecteur position
initiale
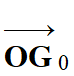 :
( y0 = 0 m)
:
( y0 = 0 m)
-
Vecteur vitesse
initiale :
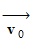 (voy = 0 m / s)
(voy = 0 m / s)
-
Référentiel d’étude :
référentiel
terrestre supposé galiléen
-
Repère d’espace :
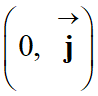
-
Bilan des forces : :
P =
m .
g
:
P =
m .
g
-
Représentation à
l’instant t :
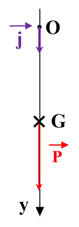
- Deuxième loi de Newton :
|
Dans un référentiel galiléen, la
somme des vecteurs forces 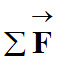
appliquées à un
système S, de masse m et de centre de masse G,
est égal au
produit de sa masse m par le vecteur accélération
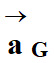
de son centre de
masse.
|
|
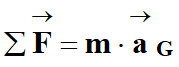
|
Valeur des
forces F en newton (N)
|
|
Valeur de la
masse m en kilogramme (kg)
|
|
Valeur de
l’accélération aG en mètre par
seconde au carré
(m . s–2)
|
-
Référentiel d’étude :
référentiel terrestre supposé galiléen
-
Repère d’espace :
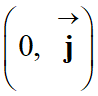
-
La deuxième loi de Newton appliquée au système
S, dans le référentiel
galiléen permet d’écrire :
-
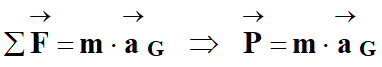
-
Comme :
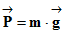
-
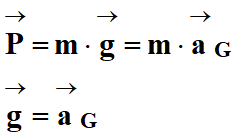
-
En utilisant les notations simplifiées :
-
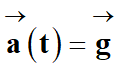
-
Le vecteur accélération est
vertical et orienté vers le bas (comme l’axe
Oy)
-
Coordonnées du vecteur
accélération :
-
ay =
g = cte
►
la bille est soumise à une force
constante, son poids
 .
.
-
Elle est en chute libre.
►
Les différentes courbes :
-
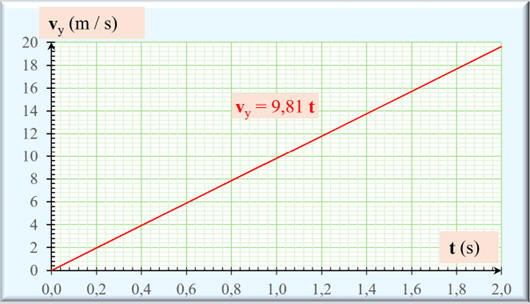
La courbe 1 :
vy
= g
(t)
-
Comme le mouvement étudié est
rectiligne uniformément accéléré, l’accélération est constante au cours du
temps.
-
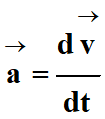
-
La détermination du vecteur
vitesse nécessite de rechercher la primitive par rapport au temps de chaque
coordonnée du vecteur accélération en tenant compte des conditions initiales.
-
On cherche les primitives des
équations précédentes.
-
Il apparaît des constantes qui
sont liées aux conditions initiales.
-
Les constantes d’intégration
apparues dans les primitives sont liées aux conditions initiales :
-
c’est-à-dire les coordonnées du
vecteur vitesse
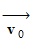 à
l’instant initial.
à
l’instant initial.
-
Or
ay
= g
-
On en déduit la relation
suivante :
-
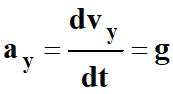
-
Par la recherche d’une primitive :
|
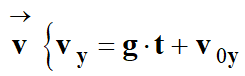
|
D’après les
conditions
initiales
|
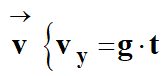
|
-
La coordonnée de la vitesse
vy
est une fonction linéaire du temps.
-
La courbe 2 :
y
= f
(t)
-
Le vecteur vitesse 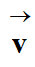 est la
dérivée par rapport au temps du vecteur position
est la
dérivée par rapport au temps du vecteur position
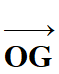
-
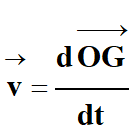
-
On opère de la même façon :
|
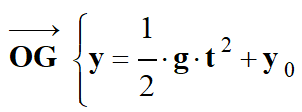
|
D’après les
conditions
initiales
|
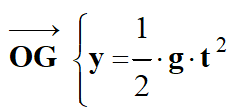
|
-
La courbe c est un arc de parabole :
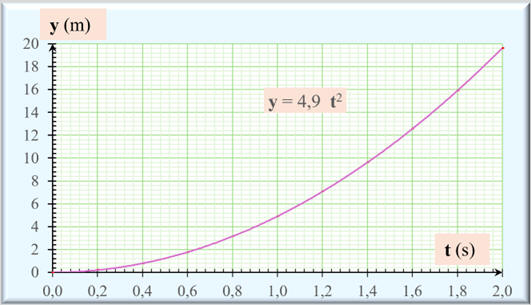
-
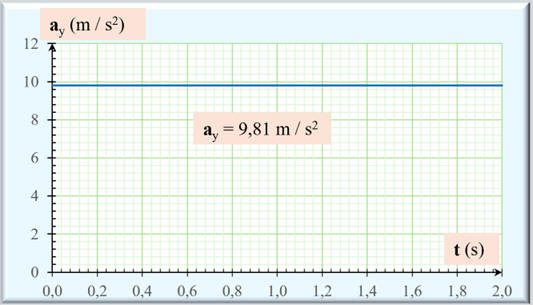
La courbe 3 :
a =
h
(t)
-
Le mouvement est rectiligne
uniformément accéléré.
-
Le vecteur accélération est un
vecteur constant (même direction, sens et valeur au cours du temps).
-
La grandeur
ay
est constante au cours du temps.
-
Cela correspond à la courbe 3.




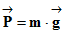
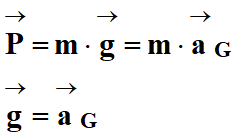
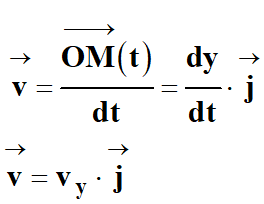
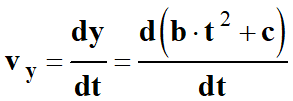
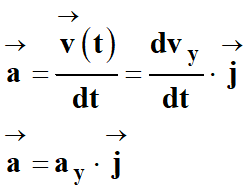
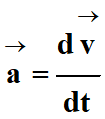

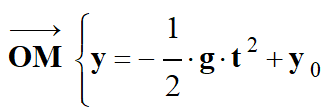
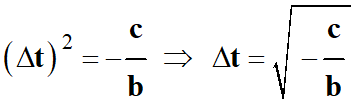
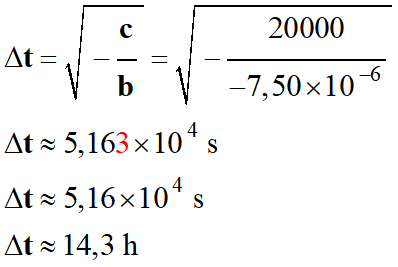





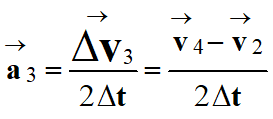
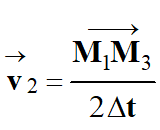

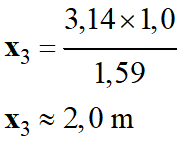
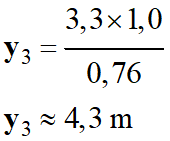
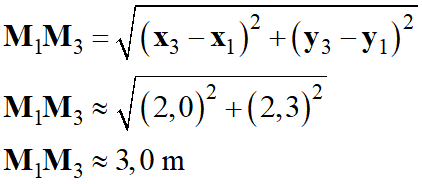
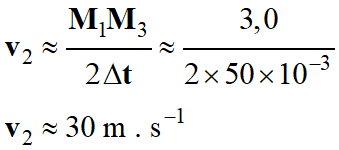
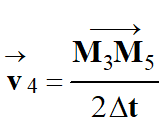

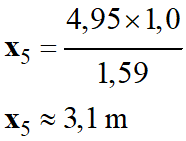
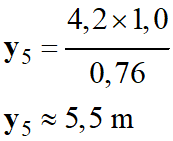
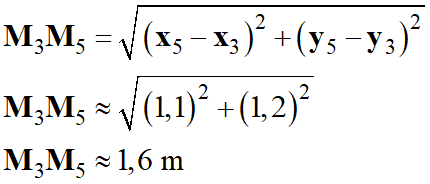
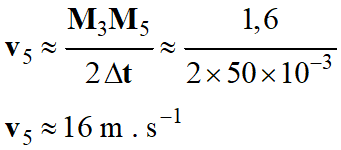
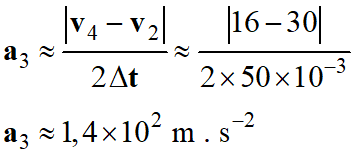


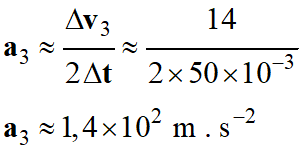






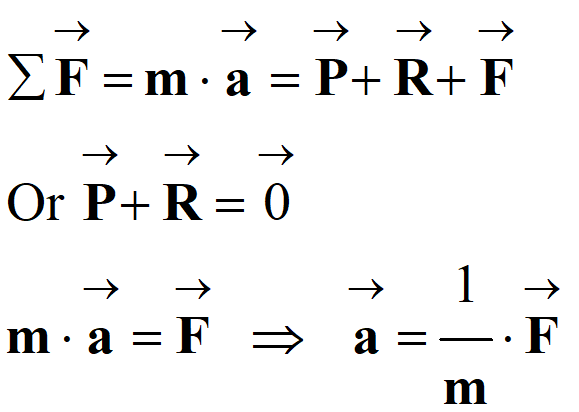

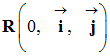
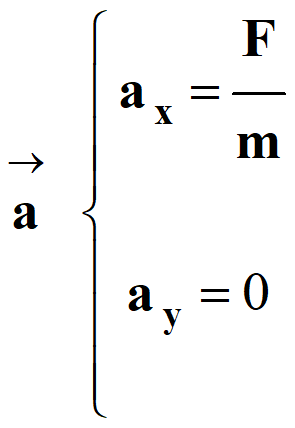
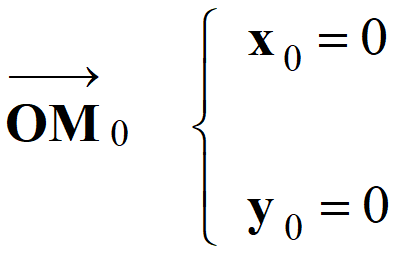
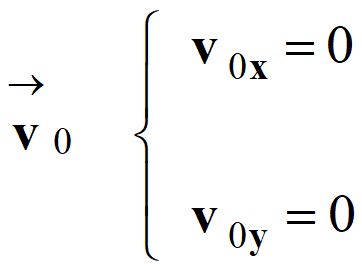
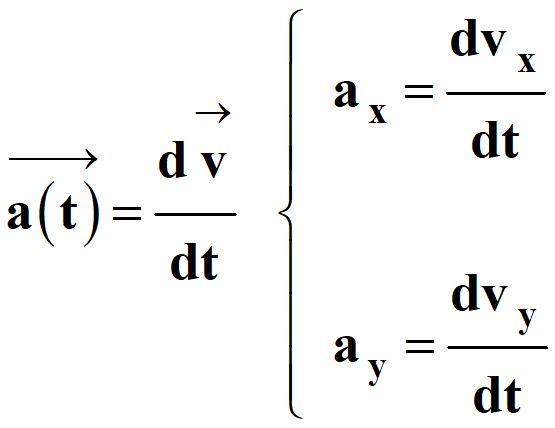
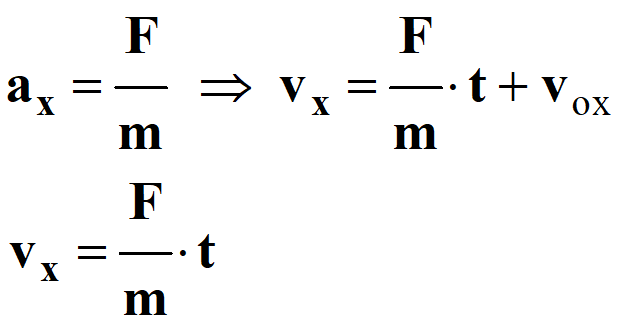
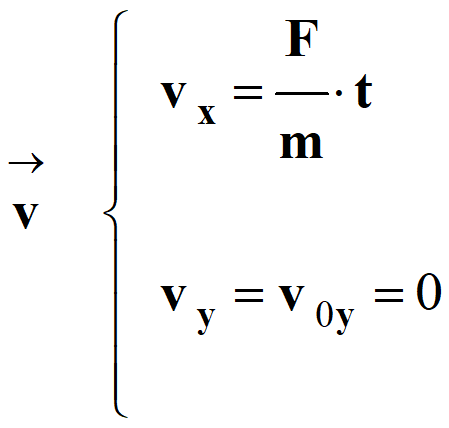
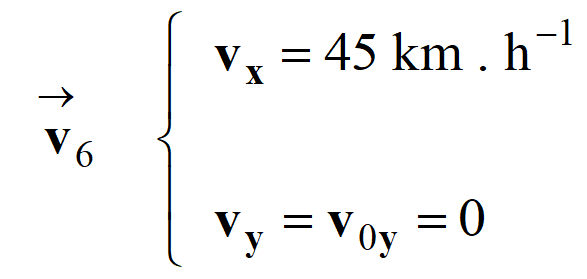
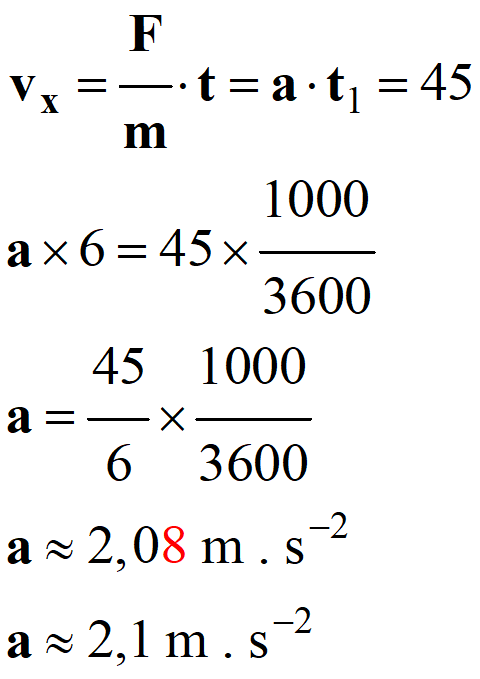
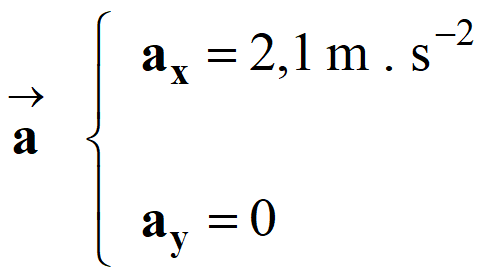
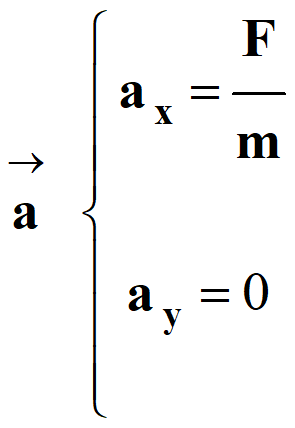
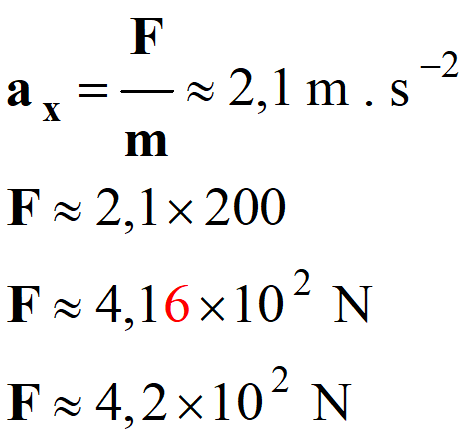

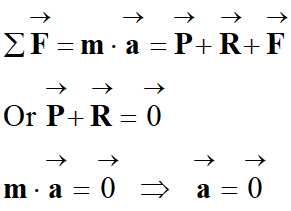
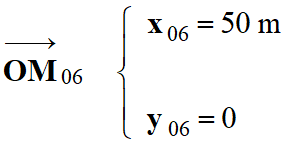 et vecteur vitesse initiale :
et vecteur vitesse initiale :