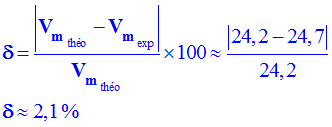I- But.

-     Déterminer le volume molaire du butane gazeux dans les conditions de température et de pression du laboratoire.

II- Expérience.

1)- Manipulation.

Première étape :

-     Prendre une recharge de butane, la peser à l’aide d’une balance et noter la valeur de sa masse : m₁ ≈ 389,12 g

-     Remplir d’eau une éprouvette graduée de 250 mL.

-     Remplir le cristallisoir d’eau aux ¾ environ.

-     Retourner l’éprouvette graduée sur le cristallisoir (l’éprouvette doit être remplie d’eau).

Deuxième étape :

-     À l’aide du tube en plastique, remplir l’éprouvette graduée de butane (gaz) par déplacement de liquide.

-     Lorsque le volume de gaz est de 200 mL, arrêter de remplir.

-     Laisser reposer quelques minutes, puis noter la valeur exacte du volume de butane à l’état gazeux :

-     V =  225 mL      .

-     Après avoir séché la recharge la peser et noter la nouvelle valeur de la masse :  m₂ ≈ 388,60 g

2)- Exploitation.

Schématiser les différentes étapes de la manipulation en indiquant la verrerie utilisée.

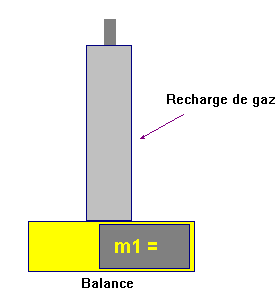
-       On pèse la recharge de butane à l’aide de la balance électronique :

-       Valeur de la masse : m₁ ≈ 389,13 g

-       Première étape :

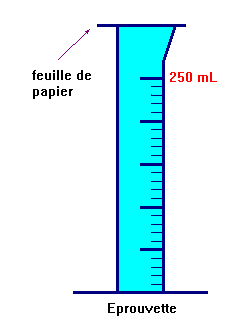
-       On remplit l’éprouvette graduée d’eau et on place délicatement une feuille de papier.

-       Deuxième étape :

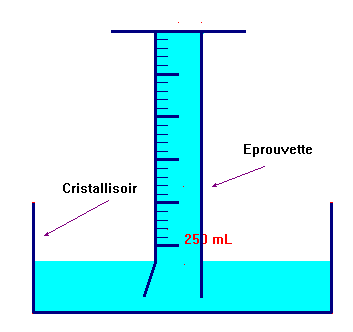
-       On retourne délicatement l’éprouvette tout en maintenant la feuille de papier

-       Puis on la plonge dans le cristallisoir et on retire la feuille de papier.

-       Troisième étape :

-       On remplit l’éprouvette de gaz butane de 200 mL environ.

-     On arrête le remplissage lorsque le liquide est au niveau de la graduation 200 mL de l'éprouvette,

-     car le butane gazeux continue de se dégager encore quelques instants.

-       On laisse reposer quelques minutes puis on note la valeur exacte du volume de butane à l’état gazeux :

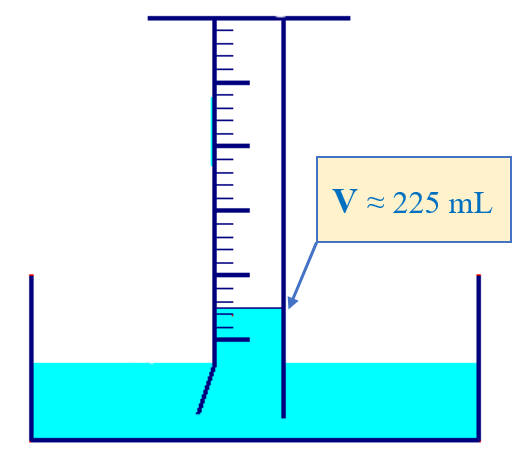
-       V ≈ 225 mL.

-       On pèse la recharge de gaz

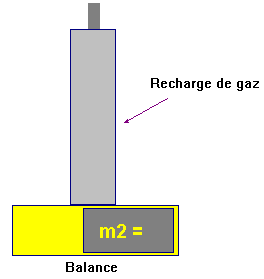
-       m₂ ≈ 388,60 g

-       Valeur de la masse :

Indiquer les conditions de température et de pression de l’expérience :

-     θ = 21 ° C                      et                     P = 1009 hPa

-    déterminer la valeur de la masse m de butane contenu dans l’éprouvette. Justifier la réponse.

-       Valeur de la masse m de butane contenu dans l’éprouvette :

-       m = m₁ – m₂

-       m = 389,13 – 388,60

-       m ≈ 0,530 g

-     Calculer la valeur de la masse molaire M du butane de formule brute C₄H₁₀.

-       Masse molaire M du butane de formule brute C₄H₁₀.

-       M = 4 M (C) + 10 M (H)

-       M = 4 x 12,01 + 10 x 1,01

-       M ≈ 58,1 g / mol

-     Déterminer la quantité de matière n de butane contenu dans l’éprouvette graduée.

-       Quantité de matière n de butane contenu dans l’éprouvette graduée.

-        

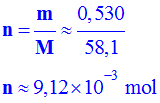
-     En déduire la valeur du volume molaire V_{m exp} du butane dans les conditions de température et de pression du laboratoire.

-       Valeur du volume molaire V_{m exp} du butane dans les conditions de température et de pression du laboratoire :

-       V_{m exp} ≈ 24,7 L / mol

-     Tirer une conclusion en utilisant la loi d’Avogadro – Ampère.

-       Loi d’Avogadro – Ampère :

-       Énoncé :

-       Des volumes égaux de gaz différents, pris dans les mêmes conditions de température et de pression, renferment le même nombre de molécules.

-       Il découle de cette loi que des volumes égaux de gaz différents, pris dans les mêmes conditions de température et de pression, renferment le même nombre de moles.

-       Ainsi :

-       Une mole de dihydrogène, une mole de butane, une mole de méthane occupent le même volume dans les mêmes conditions de température et de pression.

3)- Calcul théorique.

a)- Additif :

-     Le ° C n’est pas l’unité de température du Système International (S.I).

-     L’unité du S.I est le Kelvin (K).

-     La température absolue T s’exprime en Kelvin de symbole K .

-     Et la température θ s’exprime en degré Celsius : ° C.

-     Il existe une relation entre ces deux températures :

-     Relation : T≈θ  +  273

b)- Volume molaire théorique dans les conditions de l’expérience.

-     Sachant que dans les Conditions Normales de Température et de Pression :

-     θ = 0 °C et P = 1013 hPa, 

-     Le volume molaire V_m≈22,4 L / mol.

-     Avec la relation suivante :

Déterminer la valeur du volume molaire théorique V_{m théo} dans les conditions de l’expérience.

-       Les conditions de l’expériences : T₁ = (237 + 21) K et que P₁ = 1009 hPa

-   

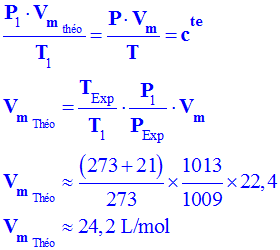
En déduire la valeur du pourcentage d’erreur :  

-       La valeur du pourcentage d’erreur :

-