|
Chim. N° 05 |
Réactions acido-basiques. Cours. |
|
|
|
|
Programme 2012 : Réaction chimique par échange de proton. Programme 2012 : Physique et Chimie Programme 2020 : Physique et Chimie |
|
QCM N° 04
Sous forme de tableau |
Exercices :
|
La liqueur de Daquin. |
Pour aller plus loin :
|
Mots clés : Acides et bases ; Produit ionique de l'eau ; constante d'acidité ; acides et bases en solution aqueuse ; réactions acido-basiques ; domaines de prédominance ; ... |
I- Produit ionique de l’eau et application.![]()
- Quelle est la valeur du pH de l’eau pure ?
- Qu’est-ce que l’eau pure ?
- Comment peut-on obtenir de l’eau pure ?
- A 25 °C, l’eau pure a un pH = 7.
- En conséquence, l’eau pure contient des ions oxonium H3O+.
- La concentration des ions oxonium peut se déduire de la définition du pH d’une solution aqueuse diluée :
- [ H3O+ ]eq = 10 – pH mol / L => [ H3O+ ]eq = 1,0 × 10 –7 mol / L
- D’où proviennent ces ions oxonium ?
- Comment peut-on expliquer la présence des ions oxonium dans l’eau pure ?
- L’eau pure est partiellement ionisée.
- Il se produit une réaction acido-basique entre deux molécules d’eau.
- Il y a un échange de protons entre deux molécules d’eau.
H2O (ℓ) + H2O (ℓ) = H3O+ (aq) + HO –(aq) (1)
- La réaction (1) est appelée autoprotolyse de l’eau.
2)- Avancement final de la réaction d’autoprotolyse de l’eau.
|
- Application 1 : à 25 °C, un volume V = 1,0 L d’eau a un pH = 7. - dresser le tableau d’avancement de la réaction. - Déterminer la valeur du taux d’avancement final de la réaction. - Calculer les quantités de matière et les concentrations des différentes espèces chimiques à l’équilibre chimique. Conclusion. - Donner l’expression du quotient de la réaction. En déduire la valeur de la constante d’équilibre de cette réaction. |
- Tableau d’avancement de la réaction d’autoprotolyse de l’eau.
|
Équation |
2 H2O (ℓ) |
= |
H3O+ (aq) |
+ HO –(aq) |
|
|
état |
Avancement
x
(mol) |
(mol) |
|
(mol) |
(mol) |
|
État
initial (mol) |
0 |
ni
=
55,6 |
|
0 |
0 |
|
Au
cours de la
transformation |
x |
ni – 2 x |
x |
x |
|
|
Avancement
final |
xf |
ni
–
2 xf |
xf |
xf |
|
|
Avancement
maximal |
xmax |
n
i
– 2
xmax
= 0 |
|
xmax |
xmax |
- En conséquence :
- Taux d’avancement final de la réaction :
| τ = | x f |
|
|
|
| x max |
- Expression de l’avancement final :
- On connaît la valeur du pH de la solution.
- En conséquence :
- xf = [ H3O+ ]eq . V avec [ H3O+ ]eq = 10– pH mol / L
- xf ≈ 1,0 × 10–7 × 1,0 => xf ≈ 1,0 × 10–7 mol
- D’autre part :
|
xmax = |
xf |
ni |
|
|
|
≈ |
|
|
|
xmax |
2 |
||
|
xmax ≈ |
27,8 mol |
||
- Taux d’avancement final :
| τ = | x f | 1,0 × 10 – 7 | |
|
|
≈ |
|
|
| xmax | 27,8 | ||
| τ ≈ |
3,6 × 10 – 9 |
||
- Quantités de matière des différentes espèces chimiques à l’équilibre :
|
Équation |
2 H2O (ℓ) |
= |
H3O+ (aq) |
+ HO –(aq) |
|
|
état |
Avancement
x
(mol) |
(mol) |
|
(mol) |
(mol) |
|
État
initial (mol) |
0 |
ni
=
55,6 |
|
0 |
0 |
|
Avancement
final |
xf |
neq
≈
55,6 |
xf
≈ 1,0
× 10 – 7
|
xf
≈
1,0
× 10 – 7
|
|
- En conséquence :
- La réaction d’autoprotolyse de l’eau est une réaction très limitée.
- Seulement 2 molécules d'eau sur 556 millions participent à la formation des ions :
- Considérons 1L d'eau pure à 25° C :
- n (H2O) ≈ 55,6 mol => n (H3O+) ≈ 1,0 × 10– 7 mol => n (HO –) ≈ 1,0 × 10 – 7 mol
- D’autre part : [H3O+]eq = [HO –]eq ≈ 1,0 × 10 – 7 mol / L
- expression du quotient de la réaction d’autoprotolyse de l’eau.
- Qr = [H3O+].[HO –]
- Lorsque l’équilibre chimique est atteint : Qr,eq = [H3O+]eq.[HO –]eq = K
- Valeur numérique de K : à 25 °C, le pH de l’eau pure vaut 7 :
- Qr,eq = K e ≈ 1,0 × 10 – 14
- La constante d’équilibre associée à l’équation d’autoprotolyse de l’eau, notée Ke est appelée produit ionique de l’eau.
- Ke = [H3O+]eq.[HO –]eq
|
- Application 2 : Calculer la valeur du produit ionique de l’eau à 25 °C. - à 25 °C, Ke ≈ 1,0 × 10 – 14. |
- La valeur du produit ionique de l’eau dépend de la température.
- Elle croît avec la température.
- Remarque : pour des raisons de commodité, on utilise le pKe.
- pK e = – log K e => K e = 10 – pKe à 25 °C, pK e ≈ 14.
|
Température en ° C |
Ke |
pKe |
|
0° |
1,1 × 10 – 15 |
14,96 |
|
25° |
1,0 × 10 – 14 |
14,00 |
|
40° |
3,0 × 10 – 14 |
13,53 |
|
60° |
9,5 × 10 – 14 |
13,02 |
|
80° |
2,5 × 10 – 13 |
12,60 |
|
100° |
5,5 × 10 – 13 |
12,26 |
4)- Les solutions aqueuses et le produit ionique de l’eau.
- Dans toutes les solutions aqueuses, le produit ionique de l’eau vaut : Ke = [H3O+]eq.[HO –]eq
- En utilisant le pKe, on peut écrire :
- pKe = - log [H3O+]eq - log [HO –]eq
- pKe = pH - log [HO –]eq
- pH = pKe + log [HO –]eq
- Ke est indépendant de la présence et de la nature des substances dissoutes.
- Ke ne dépend que de la température de la solution.
- Pour une solution aqueuse à 25 °C, on peut écrire que :
- Ke = [H3O+]eq.[HO –]eq ≈ 1,0 × 10 – 14
|
- Application 3 : Le pH d'une solution S à 25 °C est égal à 2,0. - Une solution aqueuse S1 porte l’indication : [H3O+]eq ≈ 6,5 × 10 – 5 mol / L - et une solution aqueuse S2 porte l’indication : [HO -]eq ≈ 6,5 × 10 – 5 mol / L - Que peut-on déduire de ces différentes valeurs ? |
- Étude de la solution S.
- pH = 2 => [H3O+]eq = 10 – pH = 1,0 × 10 – 2 mol / L
- D'autre part :
- Ke = [H3O+]eq.[HO –]eq ≈ 1,0 × 10 – 14
- [HO –]eq = 10 pH – pKe ≈ 1,0 × 10 – 12 mol / L
- Étude de la solution S1.
- On peut calculer la valeur du pH de la solution et la valeur de la concentration en ions hydroxyde.
- Valeur du pH de la solution S1.
- pH = – log [H3O+]eq => pH = – log (6,5 × 10 – 5) => pH ≈ 4,2
- Concentration en ions hydroxyde.
- [HO –]eq = 10 pH – pKe => [HO –]eq = 10 4,2 – 14 => [HO –]eq ≈ 1,6 × 10 – 10 mol / L
- Étude de la solution S2.
- On peut calculer la valeur de la concentration en ions oxonium puis la valeur du pH de la solution.
- Concentration en ions oxonium.
- 
- Valeur du pH de la solution S1.
- On peut utiliser l’expression suivante :
- pH = p Ke + log [HO –]eq => pH = 14 + log (5,5 × 10 – 10) => pH ≈ 4,7
5)- Solutions neutres, acides, basiques.
- Une solution neutre contient autant d'ions oxonium que d'ions hydroxyde.
- 
- À 25° C, pKe = 14 et pH = 7 pour les solutions neutres.
- Une solution acide contient plus d'ions oxonium que d'ions hydroxyde
- À 25° C, pK e = 14 et pH < 7 pour les solutions acides.
- Une solution basique contient plus d'ions hydroxyde que d'ions oxonium.
- À 25° C, pKe = 14 et pH > 7 pour les solutions basiques.
- L’équation de la réaction entre un acide AH et l’eau s’écrit :
AH (aq) + H2O (ℓ) = A– (aq) + H3O+(aq)
- cette réaction fait intervenir les couples acide / base suivants : AH (aq) / A– (aq) et H3O+(aq) / H2O (ℓ)
- La constante d’équilibre associée à cette réaction est appelée constante d’acidité notée KA.
- Expression :
-

- constante d’acidité du couple : AH (aq) / A – (aq)
- Remarque 1 : La constante d’acidité dépend de la température.
- Remarque 2 : On peut utiliser le
pK
A.
- pKA = - log KA => KA = 10 - pKA
- D’autre part :
- généralisation :
- Pour tout couple Acide / Base, noté A / B tel que :
|
A (aq) + H2O (aq) = B (aq) + H3O+(aq) |
|
Acide Base conjuguée |
- 
2)- Constantes d’acidité des couples de l’eau.
|
- Application 4 : - Déterminer les valeurs des constantes d’acidité KA1 et KA2 des couples (1) et (2) de l’eau : - H3O+(aq) / H2O (ℓ) et H2O (ℓ) / HO - (aq) - En déduire les valeurs
de pKA1 et
pKA2. |
- Étude du couple (1).
H3O+(aq) + H2O (ℓ) = H3O+(aq) + H2O (ℓ)
- 
- étude du couple (2).
H2O (ℓ) + H2O (ℓ) = H3O+(aq) + HO – (aq)
- KA2 = [H3O+]eq . [HO –]eq = Ke = 1,0 × 10 – 14
- KA2 = 1,0 × 10 – 14 et pKA2 = 14
III- Comportement des acides et des bases en solution
aqueuse.![]()
1)- Comportement des solutions acides.
|
- Application 5 :
Comparaison
du comportement des acides en solution. On donne :
- écrire les équations des réactions de ces acides avec l’eau. - Calculer le taux d’avancement final pour chaque réaction. - Classer les acides par ordre de dissociation croissante. - Tirer une conclusion générale. |
- équations des réactions de ces acides avec l’eau.
HCOOH (aq) + H2O (ℓ) = H3O+(aq) + HCOO – (aq) (1)
CH3COOH (aq) + H2O (ℓ) = H3O+(aq) + CH3COO – (aq) (2)
- Taux d’avancement final pour chaque réaction et Tableau d’avancement de la réaction :
|
Équation |
AH (aq) + |
H2O (ℓ) |
= |
A– (aq) |
+ H3O+(aq) |
|
|
état |
Avancement
x
(mmol) |
mol |
mol |
|
mol |
mol |
|
État
initial (mol) |
0 |
ni
= C.V |
excès |
|
0 |
ε |
|
Au
cours de la
transformation |
x |
ni – x |
excès |
x |
x +
ε |
|
|
Avancement
final |
xf |
ni – xf |
excès |
xf |
xf |
|
|
Avancement
maximal |
xmax |
ni – xmax
= 0 |
excès |
|
xmax |
xmax
|
-

- 
- L’acide méthanoïque est plus dissocié que l’acide éthanoïque.
- KA1 => KA2 => τ1 > τ2
|
- Pour des solutions aqueuses d’acides de mêmes concentrations : - Le pH est d’autant plus faible que le KA est grand ou le pKA petit. - Le taux d’avancement est d’autant plus grand que le KA est grand ou le pKA petit. - L’acide est d’autant plus dissocié que le KA est grand ou le pKA petit. |
- Remarque :
- Certains acides comme l’acide chlorhydrique sont totalement dissociés dans l’eau, leur taux d’avancement final est égal à 1.
- La solution aqueuse de cet acide se note :
- {H3O+(aq) + Cl – (aq)}
- Pour les acides méthanoïque et éthanoïque qui sont peu dissociés dans l'eau, on donne à la solution la notation suivante :
- Solution aqueuse d'acide méthanoïque : HCOOH
- Solution aqueuse d'acide éthanoïque : CH3COOH
2)- étude de solutions de bases.
|
- Application 6 : Comparaison du comportement des bases en solution. - On donne :
- Écrire les équations des réactions de ces bases avec l’eau. - Calculer le taux d’avancement final pour chaque réaction. - Classer les bases par ordre de dissociation croissante. - Tirer une conclusion générale. |
- Équations des réactions de ces bases avec l’eau.
CH3NH2 (aq) + H2O (ℓ) = CH3NH3 +(aq) + HO – (aq) (1)
NH3 (aq) + H2O (ℓ) = NH4 +(aq) + HO – (aq) (2)
- Taux d’avancement final pour chaque réaction.
- Tableau d’avancement de la réaction :
|
Équation |
B (aq) + |
H2O (ℓ) |
= |
BH+(aq) |
+ HO –(aq) |
|
|
état |
Avancement
x
(mmol) |
mol |
mol |
|
mol |
mol |
|
État
initial (mol) |
0 |
ni
= C.V |
excès |
|
0 |
ε |
|
Au
cours de la
transformation |
x |
ni – x |
excès |
x |
x +
|
|
|
Avancement
final |
xf |
ni – xf |
excès |
xf |
xf + ε ≈ xf |
|
|
Avancement
maximal |
xmax |
ni
– xmax
= 0 |
excès |
|
xmax |
xmax + ε ≈ xmax |
-

-

- La méthylamine est plus dissociée que l’ammoniac.
- KA1 < KA2 => τ1 > τ2
|
- Pour des solutions aqueuses de bases de mêmes concentrations : - Le pH est d’autant plus élevé que le KA est petit ou le pKA grand. - Le taux d’avancement est d’autant plus grand que le KA est petit ou le pKA grand. - La base est d’autant plus dissociée que le KA est petit ou le pKA grand. |
IV- Constante d’équilibre K des réactions acido-basiques.![]()
1)- Relation entre K et les constantes d’acidité des couples acide / base.
- Considérons la réaction entre l’acide A1H et la base A2–.
- Équation de la réaction :
A1H + A2– = A2H + A1–
- Cette réaction met en jeu les couples : A1H / A1– et A2H / A2–
- À chaque couple est associé une constante d’acidité :
- 
- 
- La réaction entre l’acide A1H et la base A2– est caractérisée par une constante d’équilibre K :
- 
- On peut exprimer K en fonction de KA1 et KA2.
- 
- 
- La constante d’équilibre de la réaction dépend des constantes d’acidité des couples acide / base mis en jeu.
2)- Réaction entre l’acide éthanoïque et l’ammoniac.
|
- Application 7 : On verse un volume V1 = 20 mL d’une solution d’acide éthanoïque de concentration C1 = 1,0 × 10 – 2 mol / L dans un volume V1 = 20 mL d’une solution d’ammoniac de concentration C2 = 1,0 × 10 – 2 mol / L. - On donne les pK A des deux couples acide / base qui interviennent : - Acide éthanoïque : pK A1 = 4,8 et Ammoniac pK A2 = 9,2. - Écrire l’équation de la réaction entre l’acide éthanoïque et l’ammoniac. - Calculer la constante d’équilibre de cette réaction. - Le pH de la solution obtenue est égal à 7. - Calculer la concentration des différentes espèces présentes à l’équilibre chimique. - Quelle conclusion peut-on tirer ?. |
- Correction :
- Équation de la réaction :
CH3COOH (aq) + NH3 (aq) = CH3COO – (aq) + NH4 +(aq) (2)
- Constante d’équilibre de cette réaction.
- 
- 
- Concentration des différentes espèces chimiques.
- Concentration en ions oxonium.
- [H3O+]eq = 10 – pH mol / L ≈ 1,0 × 10 – 7 mol / L
- Concentration en ions hydroxyde.
- [HO -]eq = 10 pH – pKe => [HO -]eq = 10 7 – 14 => [HO –]eq ≈ 1,0 × 10 – 7 mol / L
- Quantité de matière en soluté apporté : napp = C1 . V1 = C2 . V2 ≈ 2,0 × 10 – 4 mol
- Avancement final de la réaction :
|
Équation |
CH3COOH (aq) |
+ NH3 (aq) |
= |
CH3COO – (aq) |
+ NH4 +(aq) |
|
|
état |
x
(mol) |
|
|
|
|
|
|
État
initial (mol) |
0 |
napp
= C1.V1 |
napp
= C2.V2 |
|
0 |
0 |
|
Au
cours de la
transformation |
x |
napp – x |
napp – x |
x |
x |
|
|
Avancement
final |
xf |
napp
– xf |
napp – xf |
xf |
xf |
|
|
Avancement
maximal |
xmax |
napp
– x max |
napp – x max |
|
xmax |
xmax |
- Expression de K en fonction de xf.
- 
- expression de l’avancement final :
- 
- Concentration des différentes espèces chimiques. (Étude rapide)
- Concentration des ions ammonium.
- 
- Concentration des ions éthanoate.
-

- Concentration en acide éthanoïque.
-

- 
- [NH4 +]eq ≈ 160 [CH3COOH]eq
- Conclusion :
- [CH3COO -]eq ≈ [NH4 +]eq >> [CH3COOH]eq ≈ [NH3]eq
- On peut considérer que la réaction entre l’acide éthanoïque et l’ammoniac est quasi totale.
- Concentration des différentes espèces chimiques. (Étude détaillée)
- Concentration des ions ammonium.
- 
- Concentration des ions éthanoate.
- 
- d’autre part :
- Concentration en acide éthanoïque.
-

- Concentration en ammoniac.
- D’après le tableau d’avancement :
- [CH3COOH] eq ≈ [NH3] eq = 3,1 × 10 – 5 mol / L
- Conclusion :
- [CH3COO –] eq ≈ [NH4 +] eq >> [CH3COOH] eq ≈ [NH3] eq
- On peut considérer que la réaction entre l’acide éthanoïque et l’ammoniac est quasi totale.
- On peut écrire :
CH3COOH (aq) + NH3 (aq) → CH3COO – (aq) + NH4 +(aq) (2)
- Conclusion générale :
L’ordre de grandeur de la constante d’équilibre K d’une réaction chimique permet de savoir si la transformation chimique est totale, équilibrée ou très limitée. -
Si K
≥
10 4
la transformation
chimique est quasi totale. - Si K ≈ 1 la transformation chimique est équilibrée. - Si K ≤ 10 – 4 la transformation chimique est très limitée. |
V- Diagramme de distribution et domaines de prédominance.![]()
- La relation :
-

- qui découle de la réaction :
|
A (aq) + H2O (ℓ) = B (aq) + H3O+(aq) |
|
Acide Base conjuguée |
- Permet de considérer trois cas :
- Premier cas : si
- L'acide et la base conjuguée ont la même concentration.
- Deuxième cas : si
- La base B est l'espèce prédominante
- Troisième cas : si
- L’acide A est l’espèce prédominante.
- Exemple : couple CH3COOH / CH3COO –
- représentation sur un axe horizontal : couple AH / A–.

2)- Application aux indicateurs colorés de pH. (En relation avec le TP de chimie N° 5)
- Les indicateurs colorés sont constitués par des couples acide faible / base faible dont les espèces conjuguées ont des teintes différentes.
- Écriture symbolique :
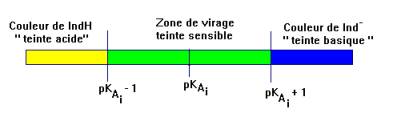
- On admet, de façon générale, que l'indicateur coloré prend sa teinte acide si :
- On admet, de façon générale, que l'indicateur prend sa teinte basique si :
- 
- Dans la zone de pH, comprise entre pKAi – 1 ≥ pH ≥ pKAi + 1, l’indicateur coloré prend sa teinte sensible.
- Les couleurs des teintes acide et basique se superposent.
- Cette zone est appelée zone de virage de l’indicateur coloré.
- La séance de TP chimie N° 5 permet de déterminer la valeur du pKAi du B.B.T.
- Domaine de prédominance : : zone de virage : 6,0 – 7,6.
- Remarque : la zone de virage est inférieure à 2 unités pH car la teinte acide est jaune et la teinte basique est bleue.
- L’œil peut bien distinguer les deux couleurs.
- Il se peut que la zone de virage soit supérieure à 2 unités pH si l’œil a du mal à distinguer les deux couleurs.
|
QCM N° 04
Sous forme de tableau |
|
La liqueur de Daquin. |