Chap. N° 20 Exercices 2024 : La lumière : un flux de photons

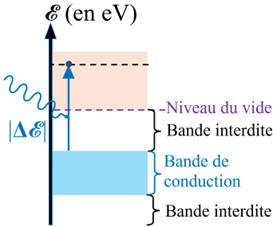
Contrairement à un atome isolé, pour lequel seuls quelques niveaux d'énergie électroniques sont autorisés, dans le cas de métal, les niveaux d'énergie dans un métal peuvent prendre toutes les valeurs comprises dans certains intervalles, les « bandes d'énergie » séparées par des « bandes interdites».

La dernière bande d'énergie « contenant » des électrons est la « bande de conduction ».

Si l’on apporte assez d’énergie au métal, un électron de la bande de conduction peut en être extrait en atteignant le « niveau du vide » correspondant à la situation où l'électron est immobile et n’est plus sous l'influence du métal.

S’il gagne encore de l'énergie cet électron isolé peut obtenir une énergie cinétique quelconque.

La figure ci-dessous représente une partie du diagramme énergétique pour un métal et une transition quantique y est repérée.

On considère un métal dont le travail d'extraction, c'est-à-dire l'énergie minimale qu’il faut lui fournir pour extraire l'un de ses électrons est noté W_e.

diagramme énergétique

a)- Reproduire le diagramme et y repérer le travail d'extraction de W_e ainsi que l'énergie cinétique ℰ_C de l'électron extrait du métal dans l'état final de la transition.

b)- En déduire par un bilan d'énergie la relation entre |Δℰ|, W_e et ℰ_C (relation d’Einstein).

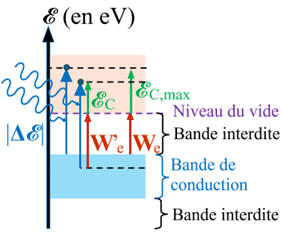
c)- Expliquer pourquoi d'après le diagramme, l'énergie cinétique ℰ_C acquise par l'électron extrait est la valeur maximale ℰ_C,max pouvant être obtenue avec le photon considéré. On pourra représenter sur le diagramme une autre transition possible avec le même photon.

d)- On note υ la fréquence de la lumière associée aux photons et υ₀ la fréquence seuil du métal. Montrer que l'on peut écrire : ℰ_C,max = h . (υ - υ₀).

2)- Correction.

a)- Exploitation du diagramme énergétique.

diagramme énergétique

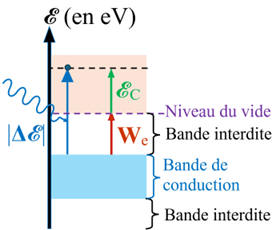
- Travail d'extraction : W_e

- La grandeur W_e représente l’énergie minimale qui permet d’arracher un électron d’un métal pour extraire un électron libre (électron le moins lié) proche de la surface du métal.

- Énergie cinétique : ℰ_C = ℰ_C,max dans ce cas.

- L’énergie cinétique d’un électron arraché est maximale pour un électron libre (électron le moins lié) proche de la surface du métal.

b)- Bilan d'énergie

- La relation entre |Δℰ|, W_e et ℰ_C (relation d’Einstein).

► Travail d’extraction : W_extraction. (ou W_e)

- L’énergie minimale qui permet d’arracher un électron d’un métal est égale au travail à fournir pour extraire un électron libre proche de la surface du métal.

- Cette énergie est appelée travail d’extraction, notée W_extraction (ou W_e)

- Elle diffère d’un métal à un autre. C’est une grandeur caractéristique d’un métal.

- Si l’énergie du photon est supérieure au travail d’extraction W_extraction(ou W_e), l’excédent d’énergie est emporté par cet électron sous forme d’énergie cinétique.

- L’arrachage d’autres électrons nécessite une plus grande énergie.

- Pour une même radiation lumineuse, l’énergie de l’électron arraché est plus faible.

- En conclusion :

- L’énergie cinétique d’un électron arraché est maximale pour un électron libre proche de la surface du métal.

- Schéma :

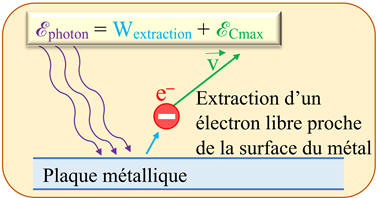
Travail d’extraction;: Wextraction

- Équation de conservation de l’énergie : Équation d’EINSTEIN de l’effet photoélectrique.

- ℰ_photon = W_extraction + ℰ_Cmax

- Avec :

- ℰ_photon = h . υ_photon et

- Tableau :

ℰ_photon = W_extraction + ℰ_Cmax
υ_photon	La fréquence du photon en hertz (Hz)
W_extraction	Travail d’extraction en joule (J) ou électron-volt (eV) 1 eV = 1,60 × 10^–19 J
m_e	Masse de l’électron : m_e = 9,109 × 10^–31 kg
v_max	Vitesse maximale de l’électron en mètre par seconde (m . s^–1)
h	Constante de Planck : h = 6,626 × 10^–34 J . s

- Dans le cas présent, on peut écrire :

- |Δℰ| = W_e + ℰ_C

- |Δℰ| = W_e + ℰ_C,max

c)- Explication du diagramme,

- Si on considère des électrons plus liés, le photon considéré peut produire la transition d’un électron d’énergie plus basse que précédemment.

- L’arrachage de cet électron nécessite un plus grand travail d’extraction W’_e.

- De ce fait l’énergie cinétique ℰ_C de cet électron sera plus faible.

- Pour une même radiation lumineuse, l’énergie de l’électron arraché est plus faible.

- Énergie cinétique ℰ_C acquise par l'électron extrait.

- Valeur maximale de l’énergie cinétique : ℰ_C,max

- ℰ_C < ℰ_C,max

- Représentation sur le diagramme d’une autre transition possible avec le même photon.

diagramme énergétique

d)- Relation : ℰ_C,max = h . (υ - υ₀).

- La grandeur |Δℰ| représente l’énergie apportée par le photon de fréquence υ.

- |Δℰ| = h . υ

- |Δℰ| = W_e + ℰ_C,max

- h . υ = W_e + ℰ_C,max

- Fréquence de la lumière associée aux photons : υ

- Fréquence seuil du métal : υ₀

- Pour un métal donné, l’effet photoélectrique se produit lorsque la fréquence ν de la radiation est supérieure à la fréquence de seuil ν₀.

- Lorsque la fréquence du photon incident est égale ν₀, l’électron est extrait avec une énergie cinétique nulle.

- En conséquence :

- h . υ₀ = W_e

- h . υ = W_e + ℰ_C,max

- h . υ = h . υ₀ + ℰ_C,max

- ℰ_C,max = h . (υ - υ₀)

- La fréquence de seuil ν₀ est une grandeur caractéristique du métal considéré.

- On remarque que lors de l’effet photoélectrique, l’énergie cinétique maximale ℰ_C,max augmente avec la fréquence υ des photons incidents.

► Fréquence de seuil et longueur d’onde de seuil :

- La fréquence de seuil ν₀ est une grandeur caractéristique du métal considéré.

- La fréquence de seuil détermine le seuil énergétique nécessaire pour déclencher l'effet photoélectrique.

- La fréquence de seuil ν₀ est la fréquence minimale d'un photon incident nécessaire pour arracher un électron d'un métal.

- Si la fréquence de la lumière est inférieure à la fréquence de seuil ν₀, aucun électron ne sera éjecté, quelle que soit l'intensité lumineuse.

- Le travail d'extraction W_e est l'énergie minimale requise pour extraire un électron d'un métal.

- Cette énergie est directement liée à la fréquence du photon par la relation de Planck-Einstein :

- Énergie du photon à la fréquence de seuil : E = h . υ₀

- À la fréquence de seuil υ₀, l'énergie du photon est exactement égale au travail d'extraction.

- W_e = h . υ₀

► Exemples :

- Plaque de cuivre métal :

- Valeur du travail d’extraction du cuivre :

- W_e = 4,71 eV

- À partir de la connaissant du travail d'extraction W_e, il est possible de calculer directement la fréquence de seuil.

- On donne : 1 eV = 1,60 × 10^–19 J

- Et la constante de Planck : h = 6,626 × 10^–34 J . s

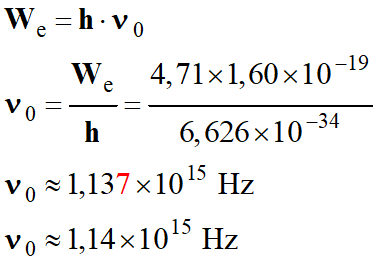
- fréquence de seuil 1,14 E15 Hz

- Longueur d’onde de seuil :

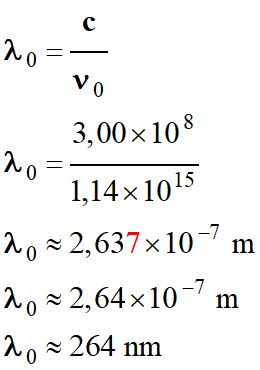
- longueur d'onde de seuil du cuivre : 264 nm

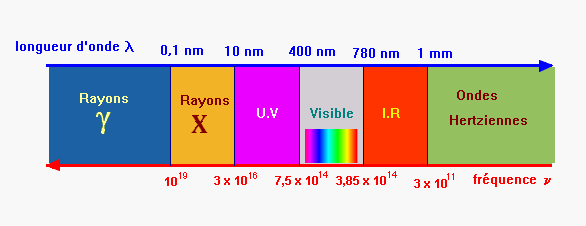
- Radiation ultraviolette.

spectre des ondes électromagnétiques

- Plaque de zinc métal :

- Exploitation graphique :

- À partir du graphique, on peut déterminer la valeur de la fréquence seuil pour la plaque de zinc :

- υ_S = υ₀ ≈ 8,8 × 10¹⁴ Hz

II- Exercice : .

1)- Énoncé.

La photocathode d'une cellule photoélectrique est éclairée par une lumière monochromatique de longueur d'onde dans le vide λ = 400 nm.

La longueur d'onde seuil de l'effet photoélectrique pour ce métal vaut λ₀ = 650 nm et on note W_e son travail d'extraction.

a)- Établir, par un bilan d'énergie, la relation entre l'énergie cinétique maximale ℰ_C,max des électrons émis par la photocathode et la fréquence υ de la lumière incidente.

b)- Déterminer, en joule J, la valeur du travail d'extraction W_e d'un électron pour le métal de la photocathode.

c)- Estimer la valeur maximale de l'énergie cinétique d'un photoélectron dans la situation considérée.

2)- Correction.

a)- Bilan d'énergie entre l'énergie cinétique maximale ℰ_C,max des électrons émis par la photocathode et la fréquence υ de la lumière incidente.

- Schéma de la situation :

Travail d’extraction;: Wextraction

- Équation de conservation de l’énergie : Équation d’EINSTEIN de l’effet photoélectrique.

- ℰ_photon = W_extraction + ℰ_Cmax

- Avec :

- ℰ_photon = h . υ_photon et

- Tableau :

ℰ_photon = W_extraction + ℰ_Cmax
υ_photon	La fréquence du photon en hertz (Hz)
W_extraction	Travail d’extraction en joule (J) ou électron-volt (eV) 1 eV = 1,60 × 10^–19 J
m_e	Masse de l’électron : m_e = 9,109 × 10^–31 kg
v_max	Vitesse maximale de l’électron en mètre par seconde (m . s^–1)
h	Constante de Planck : h = 6,626 × 10^–34 J . s

- Dans le cas présent :

- Lorsque l’énergie fournie par le photon est supérieure ou égale au travail d’extraction W_e d’un électron l’effet photoélectrique peut se produire.

- ℰ_photon = W_e + ℰ_Cmax

- ℰ_photon = h . υ

b)- Valeur du travail d'extraction W_e d'un électron pour le métal de la photocathode.

- Le travail d’extraction W_e correspond à l’énergie minimale que doit posséder le photon incident pour extraire un électron du métal.

- Dans ce cas, l’énergie cinétique ℰ_C de l’électron est nulle.

- La longueur d'onde seuil de l'effet photoélectrique pour ce métal vaut λ₀ = 650 nm et on note W_e son travail d'extraction

- W_e = h . υ₀

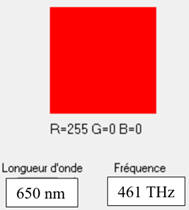
- Longueur d’onde de seuil : λ₀ = 650 nm

- Couleur de la radiation :

radiation rouge : 650 nm

- Relation :

- relation fondamentale

- Travail d'extraction :

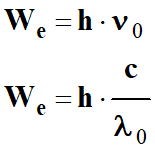
- Application numérique :

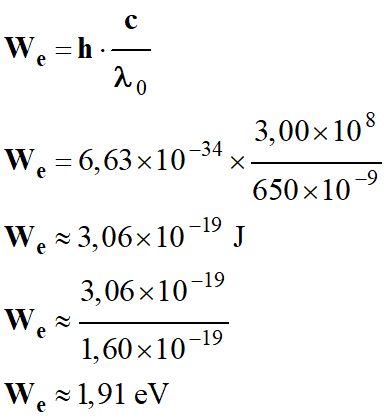
- We = 1,91 eV

- W_e en joule J et eV

c)- Valeur maximale de l'énergie cinétique d'un photoélectron dans la situation considérée.

- Pour un métal donné, l’effet photoélectrique se produit lorsque la longueur d’onde de la radiation mise en jeu est inférieure à la longueur d’onde de seuil λ₀.

- Dans le cas présent λ = 400 nm < λ₀.

- L’énergie du photon est supérieure au travail d’extraction W_e et l’excédent d’énergie est emporté par cet électron sous forme d’énergie cinétique.

- L’énergie cinétique d’un électron arraché est maximale pour un électron libre proche de la surface du métal.

- Équation de conservation de l’énergie : Équation d’EINSTEIN de l’effet photoélectrique.

- ℰ_photon = h . υ = W_e + ℰ_Cmax

- Valeur maximale de l'énergie cinétique :

- ℰ_Cmax = h . υ - W_e

- ℰ_Cmax = h . υ - h . υ₀

- ℰ_Cmax = h . (υ - υ₀)

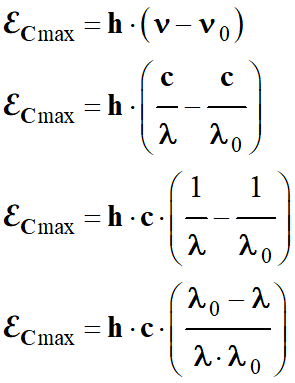
- ECmax

- Application numérique :

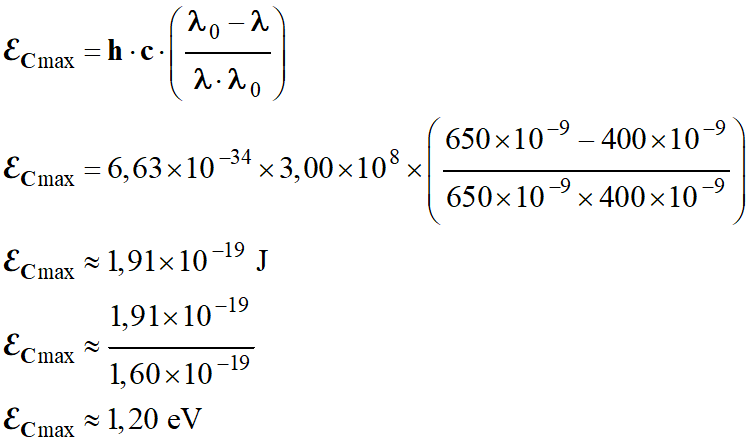
- ECmax = 1,20 eV

- Spectre de la lumière : Couleur des différentes radiations

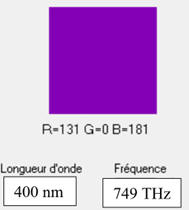
violet : 400 nm radiation rouge : 650 nm

III- Exercice :Émission des électrons par une cathode au césium.

1)- Énoncé.

La cathode d'une cellule photoélectrique, formée de césium, est éclairée par une lumière monochromatique de longueur d'onde dans le vide λ = 405 nm.

Cellule photoélectrique ;

DONNÉE : Longueur d’onde de seuil, dans le vise, du césium : λ₀ = 592 nm

a)- Déterminer la valeur du travail d'extraction W_e du césium.

b)- Estimer la valeur de l'énergie cinétique ℰ_Cmax que possèdent les électrons les plus rapides qui viennent d'être éjectés de la cathode.

2)- Correction.

a)- Valeur du travail d'extraction W_e du césium.

- DONNÉE : Longueur d’onde de seuil, dans le vise, du césium : λ₀ = 592 nm

- Le travail d’extraction W_e correspond à l’énergie minimale que doit posséder le photon incident pour extraire un électron du métal.

- Dans ce cas, l’énergie cinétique ℰ_C de l’électron est nulle.

- La longueur d'onde seuil de l'effet photoélectrique pour ce métal vaut λ₀ = 592 nm et on note W_e son travail d'extraction

- W_e = h . υ₀

- Longueur d’onde de seuil : λ₀ = 592 nm

- Couleur de la radiation :

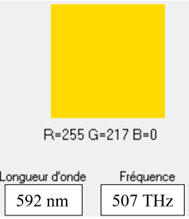
radiation jaune : 592 nm

- relation fondamentale

- Travail d'extraction :

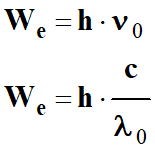
- Application numérique :

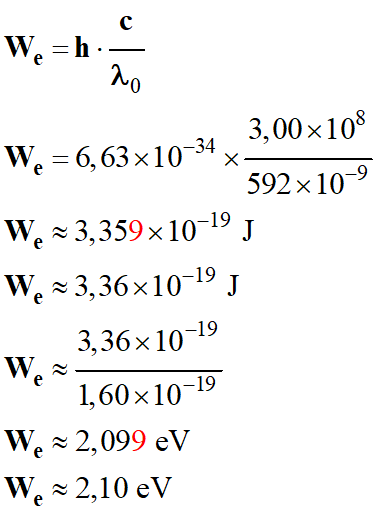
- We = 2,10 eV

b)- Valeur de l'énergie cinétique ℰ_Cmax des électrons les plus rapides.

- Si l’énergie du photon est supérieure au travail d’extraction W_e l’excédent d’énergie est emporté par cet électron sous forme d’énergie cinétique.

- Pour un métal donné, l’effet photoélectrique se produit lorsque la longueur d’onde de la radiation mise en jeu est inférieure à la longueur d’onde de seuil λ₀.

- Dans le cas présent λ = 405 nm < λ₀ = 592 nm

- L’énergie du photon est supérieure au travail d’extraction W_e et l’excédent d’énergie est emporté par cet électron sous forme d’énergie cinétique.

- L’énergie cinétique d’un électron arraché est maximale pour un électron libre proche de la surface du métal.

- Équation de conservation de l’énergie :

- Équation d’EINSTEIN de l’effet photoélectrique.

- ℰ_photon = h . υ = W_e + ℰ_Cmax

- Valeur maximale de l'énergie cinétique :

- ℰ_Cmax = h . υ - W_e

- ℰ_Cmax = h . υ - h . υ₀

- ℰ_Cmax = h . (υ - υ₀)

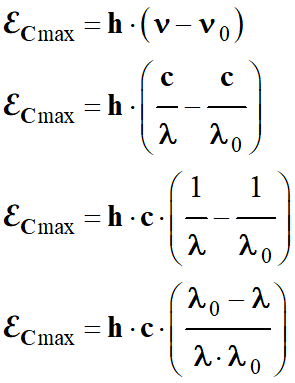
- ECmax

- Application numérique :

- ECmax = 0,970 eV

- Une partie du spectre de la lumière blanche :

violet : 405 nm radiation jaune : 592 nm

IV- Exercice : Expérience de Hallwachs.

1)- Énoncé.

Le travail d'extraction du zinc vaut W_e = 3,40 eV.

a)- Interpréter qualitativement l'effet photoélectrique à l'aide du modèle particulaire de la lumière.

b)- Calculer la fréquence seuil υ₀ du zinc pour l'effet photoélectrique. En déduire la valeur de la longueur d'onde seuil λ₀ du zinc.

c)- Déterminer l'énergie cinétique maximale ℰ_Cmax des électrons éjectés de la plaque lorsque celle-ci est éclairée par un rayonnement UV de longueur d'onde dans le vide λ = 254 nm, correspondant à une raie d’émission d'une lampe à vapeur de mercure.

d)- Si on interpose une plaque de verre, entre la lampe à vapeur de mercure et la plaque de zinc, on remarque que l'effet photoélectrique cesse. Proposer une explication à cette observation.

2)- Correction.

a)- Interprétation qualitative de l'effet photoélectrique.

- Modèle particulaire de la lumière.

- L’extraction des électrons n’est possible que si l’énergie fournie par la lumière est suffisante.

- Dans le cas du zinc, il faut des radiations UV.

- Le nombre d’électrons arrachés est proportionnel à l’intensité lumineuse du rayonnement.

- L’énergie cinétique des électrons arrachés est indépendante de l’intensité lumineuse du rayonnement.

- L’énergie cinétique augmente lorsque la fréquence de la lumière incidente augmente.

- Le modèle ondulatoire de la lumière ne permet pas d’expliquer ces différentes observations.

- En 1905, pour expliquer l’effet photoélectrique, A. EINSTEIN propose un aspect particulaire pour la lumière.

- Chaque particule possède une énergie : E = h . υ.

- Cette particule sera appelée photon quelques années plus tard.

- A. EINSTEIN explique que l’énergie du photon sert en partie à arracher l’électron de l’atome, le reste étant emporté par l’électron sous forme d’énergie cinétique.

► L’effet photoélectrique :

- C’est le phénomène d’éjection d’électrons d’un métal sous l’effet de radiations lumineuses.

- Pour un métal donné, cet effet se manifeste que pour des photons d’énergie suffisamment grande.

- L’effet est quasiment instantané.

- Il se manifeste si l’énergie du photon est supérieure au travail d’extraction d’un électron du métal W_extraction.

- L’énergie excédentaire est emportée par l’électron sous forme d’énergie cinétique.

► Le photon :

- La lumière peut être décrite comme un flux de photons.

- Un photon possède une masse nulle et se propage à la célérité c de la lumière dans le vide.

c = 299 792 458 m . s^–1

► Énergie d’un photon.

- L’énergie de la lumière est transportée par des photons qui présentent un aspect particulaire et un aspect ondulatoire.

- L’énergie d’un photon est donnée par la relation :

- E = h . υ

- L’énergie E représente l’aspect particulaire du photon.

- La fréquence υ représente son aspect ondulatoire.

- Pour une onde électromagnétique de fréquence υ et de longueur d’onde λ dans le vide,

- On peut écrire :

Relation de PLANCK-EINSTEIN :
h	La grandeur h est la constante de Planck : h = 6,626 × 10^–34 J . s
υ	La fréquence υ en hertz (Hz)
λ	La longueur d’onde dans le vide λ en mètre (m)
c	La célérité de la lumière dans le vide : c = 3,00 × 10⁸ m . s^{– 1}
E	Énergie E en joule (J) ou électronvolt (eV) 1 eV = 1,60 × 10^–19 J

- Cette relation met en évidence le caractère à la fois :

- Particulaire : photon, particule de masse nulle et d’énergie E_photon.

- Ondulatoire : fréquence υ, longueur d’onde λ.

- On parle de dualité onde-corpuscule.

b)- Fréquence seuil υ₀ du zinc pour l'effet photoélectrique.

- Travail d'extraction du zinc : W_e = 3,40 eV

- Le travail d’extraction W_e correspond à l’énergie minimale que doit posséder le photon incident pur extraire un électron du métal.

- Dans ce cas, l’énergie cinétique ℰ_C de l’électron est nulle.

- W_e = h . υ₀

- Fréquence υ₀ seuil :

- Fréquence υ0 seuil

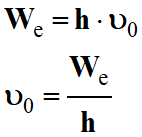
- Application numérique :

- fréquence seuil : 8,21 E14 Hz

- Valeur de la longueur d'onde seuil λ₀ du zinc :

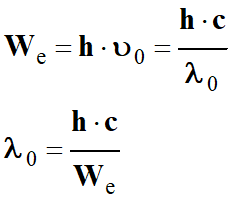
- longueur d'onde seuil

- Application numérique :

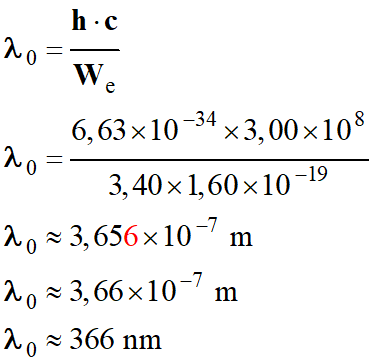
- longueur d'onde seuil : 366 nm

- C’est une radiation qui appartient au domaine UV.

c)- Énergie cinétique maximale ℰ_Cmax des électrons éjectés de la plaque.

- On éclaire la plaque avec un rayonnement UV :

- Longueur d'onde dans le vide λ = 254 nm

- Une raie d’émission d'une lampe à vapeur de mercure :

- Équation d’EINSTEIN de l’effet photoélectrique.

- ℰ_photon = h . υ = W_e + ℰ_Cmax

- Valeur maximale de l'énergie cinétique :

- ℰ_Cmax = h . υ - W_e

- Application numérique :

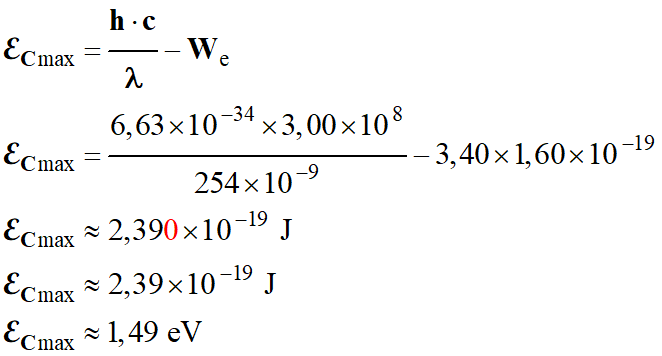
- EcMax = 1,49 eV

d)- Proposition d’une explication de cette observation.

- Pour un métal donné, l’effet photoélectrique se produit lorsque la longueur d’onde de la radiation mise en jeu est inférieure à la longueur d’onde seuil λ₀.

- On interpose une plaque de verre entre la lampe à vapeur de mercure et la plaque de zinc et on remarque que l'effet photoélectrique cesse.

- Le verre laisse passer la lumière visible mais absorbe le rayonnement UV de longueur d’onde inférieure à la longueur d’onde seuil.

- La plaque de verre empêche ainsi l’effet photoélectrique de se produire.

- Spectre de la lampe à vapeur de mercure :

- longueurs d’ondes (les plus visibles) :

- 615 nm, 580 nm, 579 nm, 577 nm, 546 nm, 492 nm, 436 nm, 405 nm (que l’on devrait voir)

Les messages de la lumière

Spectres d'émission

QCM :

Interaction Lumière-matière.

V- Exercice : Solar Impulse 2 .

1)- Énoncé.

L’avion solaire Solar impulse 2 a pour seule source d'énergie le rayonnement solaire.

DOC. 1 : Caractéristiques techniques.

Solar impulse 2

- Cellules photovoltaïques : 17248 sur une surface de 270 m².

- Moteurs électriques : nombre 4 ; puissance 17,4 chevaux chacun ; rendement : 92 %,

- Batteries : lithium polymère pour le vol de nuit.

- Masse : 2300 kg

- Vitesse maximale : 140 km .h^–1.

DOC. 2 : Conversion d’énergie au sein d’une cellule photovoltaïque.

Les cellules photovoltaïques sont généralement composées de silicium dont l'énergie de gap vaut ℰ_g = 1,12 eV.

Or, seuls les photons dont l'énergie est supérieure ou égale à ℰ_g peuvent libérer un électron qui participe au courant électrique délivré par une cellule.

Pour augmenter le nombre de photons captés, il faut diminuer l'énergie de gap, mais on récupère alors moins d'énergie par photon, car l'énergie en excès est dissipée sous forme thermique.

DOC. 3 : Répartition spectrale de la puissance surfacique du rayonnement solaire au niveau du sol terrestre.

DONNÉES :

► Caractéristiques d’une journée de traversée :

- Durée du vol : 14 h

- Puissance surfacique moyenne du rayonnement solaire réellement disponible : 450 W . m^–2.

- Énergie électrique fournie aux moteurs par les panneaux solaires au cours de la journée : 370 kWh.

a)- Déterminer la valeur du rendement des panneaux solaire de Solar Impulse 2.

b)- Porter un regard critique sur la valeur obtenue et proposer une explication au rendement limité des cellules photovoltaïques.

2)- Correction.

a)- Valeur du rendement des panneaux solaire de Solar Impulse 2.

- Durée du vol : 14 h

- Puissance surfacique moyenne du rayonnement solaire réellement disponible : 450 W . m^–2.

- Cellules photovoltaïques : 17248 sur une surface de 270 m².

- Énergie électrique fournie aux moteurs par les panneaux solaires au cours de la journée : 370 kWh.

- Panneau photovoltaïque :

panneau photovoltaïque

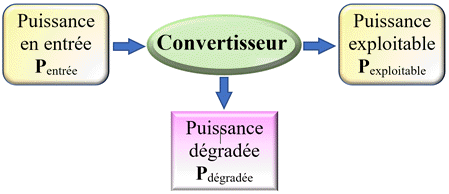
► Rendement d’une cellule photovoltaïque :

- Le rendement η d’une cellule photovoltaïque est le rapport de la puissance exploitable sur la puissance en entrée.

convertisseur d'énergie

	η sans unité
	P_exploitable en watt (W)
	P_entrée en watt (W)

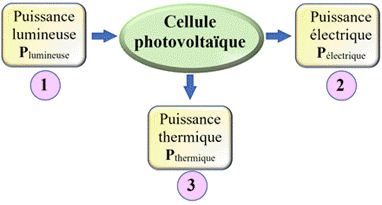
- Le rendement η d’une cellule photovoltaïque est le rapport de la puissance électrique sur la puissance lumineuse.

panneau photovoltaïque

- Avec les notations précédentes :


η	Grandeur sans unité : 0 < η ≤ 1
P_électrique	Puissance exploitable : Puissance électrique en watt (W)
P_lumineuse	Puissance en entrée : Puissance lumineuse en watt (W)

- On peut aussi utiliser les énergies :


η	Grandeur sans unité : 0 < η ≤ 1
ℰ_électrique	Énergie exploitable : Énergie électrique en joule (J)
ℰ_lumineuse	Énergie en entrée : Énergie lumineuse en joule (J)

- Dans le cas présent :

- ℰ_électrique est l’énergie électrique fournie aux moteurs électriques par les panneaux solaires aux cours d’une journée

- ℰ_électrique = 370 kWh

- ℰ_lumineuse est l’énergie reçue par les panneaux photovoltaïques au cours d’une journée :

- Durée du vol : Δt = 14 h

- Puissance surfacique moyenne du rayonnement solaire réellement disponible :

- P_s = 450 W . m^–2.

- P_s = 0,450 kW . m^–2

- Cellules photovoltaïques : 17248 sur une surface de 270 m²

- S = 270 m²

- Relation :

- ℰ_lumineuse = P_s . S . Δt

- Rendement des panneaux solaire de Solar Impulse 2 :

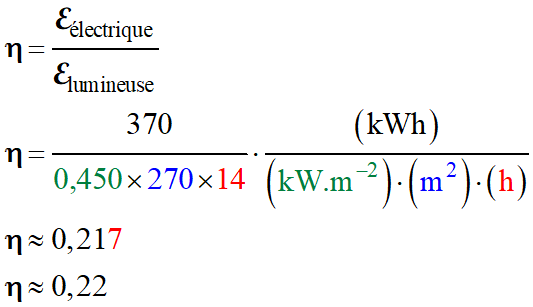
- rendement : 0,22

- Le rendement est η ≈ 22 %.

- Par rapport au rendement des moteurs électriques (η = 92 %), le rendement des panneaux photovoltaïque est faible, mais l’énergie lumineuse est inépuisable à notre échelle.

b)- Regard critique sur la valeur obtenue.

- Explication sur le rendement limité des cellules photovoltaïques.

- Le rendement des panneaux photovoltaïque est faible : η ≈ 22 %.

- Exploitation du DOC. 2 :

- Les cellules photovoltaïques sont généralement composées de silicium dont l'énergie de gap vaut ℰ_g = 1,12 eV.

- Seuls les photons dont l'énergie est supérieure ou égale à ℰ_g peuvent libérer un électron qui participe au courant électrique délivré par une cellule.

- Il existe donc une fréquence seuil υ₀.

- La fréquence de seuil ν₀ est la fréquence minimale d'un photon incident nécessaire pour libérer un électron qui participe au courant délivré par une cellule.

- Seuls les photons dont la fréquence ν est supérieure à la fréquence seuil υ₀ sont efficaces.

- Si on raisonne par rapport à la longueur d’onde λ, on peut affirmer que seuls les photons dont la longueur d’onde est inférieure à la longueur d’onde de seuil λ₀ sont efficaces.

- Valeur de la fréquence de seuil ν₀ :

- Valeur de la fréquence de seuil

- Application numérique :

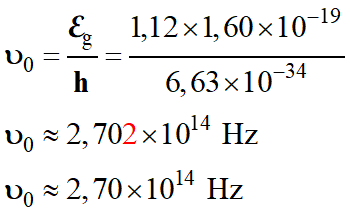
- fréquence seuil : 2,70 E14 Hz

- Pour pouvoir exploiter le graphe du DOC. 3, il faut déterminer la valeur de la longueur d’onde seuil.

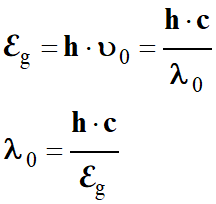
- Longueur d'onde seuil :

- Longueur d'onde seuil

- Application numérique :

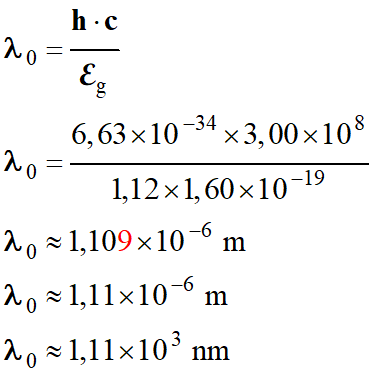
- Longueur d'onde seuil : 1,11 E-6 m

- La longueur d’onde de seuil vaut environ λ₀ ≈ 1110 nm

- Seuls les photons dont la longueur d’onde est inférieure à la longueur d’onde de seuil λ₀ ≈ 1110 nm sont efficaces

► Exploitation du graphe :

- On se position par rapport à la longueur d’onde de seuil . λ₀.

- La zone A est une partie non efficace du rayonnement solaire.

- Elle correspond à des longueurs d’onde supérieures à 1110 nm.

- La zone B correspond à la partie efficace du rayonnement.

- En dehors de la partie visible du rayonnement solaire, la puissance surfacique diminue rapidement.

- La conversion d’énergie est de moins en moins efficace à mesure que la longueur d’onde diminue.