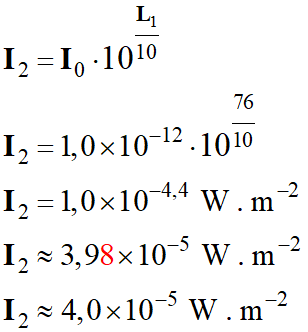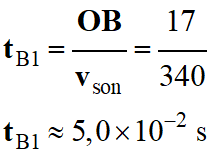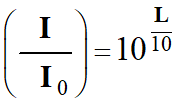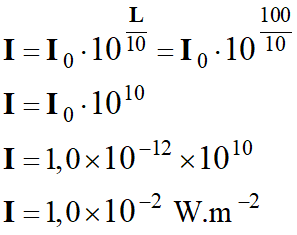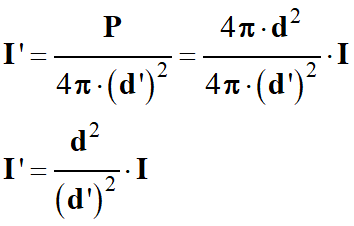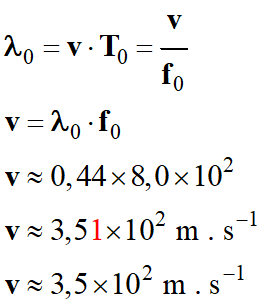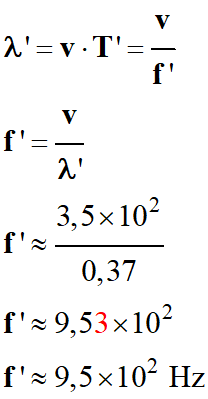Chap. N° 17 Exercices 2024 : Sons et effet Doppler
|
|
I-
Exercice :
Assister à un mini-concert.
1)- Énoncé.

Un « concert » est donné avec 2 violons.
Les niveaux d'intensité sonore L1
et L2
produits séparément par chacun des 2 instruments sont mesurés à l'aide d'un
sonomètre placé à 5,0 m des musiciens.
Les mesures donnent : L1
= 70 dB et L2
= 76 dB.
a)-
Déterminer les intensité sonores
I1
et I2
correspondant respectivement à
L1 et
L2.
b)-
En déduire l'indication du sonomètre,
placé à la distance d = 5,0 m des musiciens jouant
simultanément.
c)-
Combien de violons, produisant chacun en un
point un son de niveau sonore 70 décibels, faudrait-il pour que le niveau
d'intensité sonore résultant en ce point soit de 90 décibels ?

2)- Correction.
a)-
Détermination des intensité sonores
I1
et I2
correspondant respectivement à
L1 et
L2.
►
Intensité sonore :
I
-
Le niveau d’intensité sonore est
lié à l’amplitude du signal sonore.
-
C’est la puissance sonore reçue pour une surface donnée.
-
Plus l’amplitude du signal sonore
est élevée plus l’intensité sonore I
est grande.
-
L’intensité sonore, notée
I, caractérise l’intensité du signal
reçue par l’oreille.
-
L’intensité sonore
I est la puissance
P par unité de surface
S transportée par une onde sonore.
|

|
I
: Intensité sonore en watt par mètre carré (W . m–2)
|
|
P :
Puissance transportée par l’onde sonore en watt (W)
|
|
S
: Surface de l’onde sonore en mètre carré
(m2)
|
-
Elle s’exprime en watt par mètre
carré : W / m2 ou W. m–2
-
L’oreille humaine normale perçoit
les signaux sonores dont l’intensité est comprise entre
-
Une valeur minimale
I0 =
1,0 × 10–12
W. m–2 (seuil
d’audibilité)
-
Et une valeur maximale
Imax =
25 W. m–2 (seuil de
douleur).
►
Niveau d’intensité sonore :
L
-
Le niveau d’intensité sonore est une grandeur qui traduit la façon dont notre
oreille perçoit l’ « volume sonore » d’un son.
-
On définit le niveau d’intensité
sonore L
à partir de l’intensité associée au seuil d’audibilité.
-
Relation mathématique :
|

|
L :
Niveau d’intensité sonore en décibel (dB)
|
|
I :
Intensité du signal en watt par mètre carré (W. m–2)
|
|
I0
= 1,0
× 10–12 W. m–2 (seuil
d’audibilité)
|
-
La notation
log fait référence à la fonction
logarithme décimal.
-
Ainsi, l’échelle de niveau
d’intensité sonore L varie de
0 dB à environ 140 dB.
-
Alors que l’intensité sonore
I varie de
I0 =
1,0 ×10–12
W. m–2 à 102
W. m–2
-
Échelles de
I et L :

-
Remarque : les valeurs de
L (dB) sont plus faciles à manipuler
que les valeurs de I (W. m–2)
-
Il est possible de calculer une
intensité sonore I
à partir de la connaissance du niveau d’intensité
sonore L :
-
Relation :
|

|
L :
Niveau d’intensité sonore en décibel (dB)
|
|
I :
Intensité du signal en watt par mètre carré (W. m–2)
|
|
I0
= 1,0
x 10–12 W. m–2 (seuil
d’audibilité) aussi
Intensité
sonore de référence
|
-
DONNÉES : Les mesures donnent :
L1
= 70 dB et L2
= 76 dB.
-
Intensité sonores
I1 :
-

-
Intensité sonores
I2 :
-
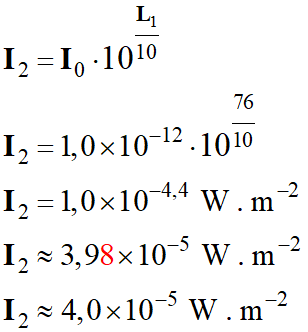
b)-
Indication du sonomètre, placé à la
distance d
= 5,0 m des musiciens jouant simultanément.
-
Lorsque les deux musiciens jouent
ensemble, les l’intensités sonores de chaque instrument s’ajoutent ( en
l’absence de phénomène d’interférences)
-
Le sonomètre mesure le niveau
d’intensité sonore
L.
-
I =
I1
+ I2
-
I ≈ 1,0 × 10–5
+ 4,0 × 10–5
-
I ≈ 5,0 × 10–5
+ W. m–2
-
Niveau d’intensité sonore
L correspondant :
-

c)-
Nombre de violons pour que le niveau
d'intensité sonore résultant en ce point soit de 90 décibels
-
On note
n
le nombre de violons :
-
On considère que pour 1 violon :
-
Le niveau d’intensité sonore
correspond à : L1
= 70 dB
-
Pour
n
violons, le niveau d’intensité sonore vaut :
L’ = 90 dB
-
Pour 1 violon :
-

-
Pour
n
violons : I’
= n
. I1
-

-
Application numérique :
-

-
Cela correspond à environ 100
violons.
-
Un bel orchestre !!!

II-
Exercice :
La raie α du spectre d’émission de l’hydrogène.
1)- Énoncé.
La raie α (alpha) du spectre d'émission de
l'hydrogène, mesurée en laboratoire, a une longueur d'onde λα = 656,28
nm.
Cette même raie a une longueur d'onde λ’ = 660,82 nm
lorsque le spectre étudié est celui de la Galaxie NGC 13 57.
Justifier que la Galaxie s'éloigne de la terre et calculer
la valeur de sa vitesse v dans la direction de visée.
- DONNÉE : Décalage Doppler relatif :


2)- Correction.
-
Mouvement de la Galaxie par rapport à la Terre :
►
Effet Doppler -Fizeau.
Le spectre de la
lumière émise par une étoile comporte des raies d’absorption caractéristiques
des éléments présents dans l’atmosphère qui l’entoure.
-
En appliquant les conséquences de
l’effet C. Doppler à la lumière, H.
Fizeau (1819-1896) a postulé en 1848 que :
-
Si une étoile
s’éloigne ou s’approche de la Terre, on doit observer un décalage de ses raies
d’absorption.
-
La mesure de ce
décalage permettrait de calculer la vitesse radiale de l’étoile.
-
Les télescopes
modernes et les outils informatiques permettent aujourd’hui de calculer les
vitesses radiales des étoiles en analysant de très nombreuses raies.
-
L’effet Doppler-Fizeau
permet de calculer la valeur de la vitesse radiale d’une étoile en comparant les
longueurs d’onde de son spectre d’absorption à celles d’un spectre de référence.
-
Lorsque l’étoile
s’éloigne de la Terre, on observe un décalage vers les grandes longueurs d’onde
c’est-à-dire vers le rouge pour les raies du visible (Redshift).
-
Lorsque l’étoile se
rapproche de la Terre, on observe un décalage vers les petites longueurs d’onde
c’est-à-dire vers le bleu pour les raies du visible (Blueshift).
-
Remarque : la vitesse
radiale d’une étoile est la vitesse à laquelle elle s’éloigne ou s’approche de
la Terre.
-
Le décalage de la
longueur d’onde dû à l’effet Doppler-Fizeau permet de calculer la valeur de la
vitesse d’éloignement ou de rapprochement d’une galaxie par rapport à la Terre.
|
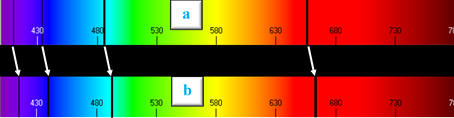
Décalage vers le rouge (Redshift) des raies entre le
spectre obtenu
pour une source et un
observateur immobile
(spectre
a
) et celui
obtenu pour un éloignement entre la
source et l’observateur
(spectre
b).
|
►
Cas de la Galaxie NGC 13 57 :
-
La raie
α du spectre d'émission de
l'hydrogène sur Terre
-
λα = 656,28
nm
-
Le spectre étudié est celui de la
Galaxie, la même raie :
-
λ’ = 660,82 nm
-
Conclusion :
-
λ’ >
λα

-
il y a un décalage vers le rouge.
-
La Galaxie NGC 13 57 s’éloigne de
la Terre.
-
Vitesse d’éloignement de cette
Galaxie :
-

-
Application numérique :
-

-
Cette vitesse a une valeur élevée,
mais elle n’est pas relativiste.

III- Exercice :
Déterminer une fréquence décalée.
1)- Énoncé.
Une source sonore émet des « bips » avec une fréquence
f = 10 Hz.
Elle est initialement en un point
O, milieu d'un segment
[AB] = 34 m et
se déplace, de A
vers B, avec
une vitesse de valeur constante vs
=34 m . s–1..

DONNÉE :
Vitesse du son dans d’air : vson
= 340 m . s–1.
a)-
Déterminer la durée
T qui sépare les émissions de 2 bips
consécutifs.
b)-
En déduire la distance
d
parcourue par la source pendant
cette durée.
c)-
Préciser à quelle date
tB1 le premier bip émis à
l'instant de date t = 0 arrive au
point B. Puis préciser à quelle date
tB2 le deuxième bip arrive
au point
B.
d)-
Calculer la fréquence
fB avec laquelle un
observateur placé en
B reçoit les
bits.
e)-
Nommer le phénomène correspondant à ce décalage de
fréquence et en citer quelques applications.

2)- Correction.
a)-
Durée
T
qui sépare les émissions de 2 bips consécutifs.
-
La
durée qui sépare les émissions de 2 bips consécutifs est appelée période
T
de la source S.
-
La période
T
d’un phénomène périodique est la durée au bout de laquelle le phénomène se
reproduit identique à lui-même.
-
L’unité de période
T
est la seconde, symbole s.
-
La fréquence
f
représente le nombre de période par seconde. On
écrit :
-

-
unité
de fréquence : Hertz : symbole Hz
-
Remarque : Pour
obtenir la fréquence en Hz, il faut pour cela exprimer la période en seconde s.
-
Application
numérique :
-

b)-
Distance
d
parcourue par la source
S
pendant cette durée.
-
Lors de l’émission du
premier bip, la source se trouve au point
O.
-
Le
deuxième bip est émis au bout de la durée :
Δt
= T
(bips consécutifs)
-
La
source se déplace à vitesse constante de
A
vers B :
: vs
= 34 m . s–1
-
La
source s’est déplacée de la distance
d :
-
Schéma de la
situation :
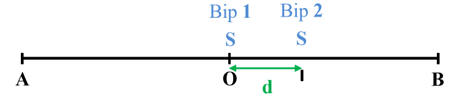
-
Application
numérique :
-
d
= vs
× Δt
-
d
= vs
× T
-
d
≈ 34 × 0,10
-
d
≈ 3,4 m
c)-
Date
tB1
le premier bip émis à l'instant de date
t = 0 arrive au point
B.
-
Le bip
se déplace à la vitesse du son :
vson =
340 m . s–1
-
Lorsque
le premier bip est émis, la source
S
occupe la position
O.
-
La distance que
parcourt de bip : distance
OB :
-
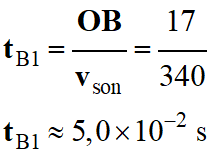
-
Date
tB2
le deuxième bip arrive au point
B.
-
Le
deuxième bip est émis, après la durée
T,
lorsque la source S
a parcouru la distance
d.
-
La distance que
parcourt le deuxième bip : distance
OB – d :
-

d)-
Fréquence
fB
avec laquelle un observateur placé en
B
reçoit les bits.
-
L’observateur immobile placé au point
B
reçoit le premier bip au temps
tB1
et
le deuxième bip au temps tB2.
-
La
période TB
pour cet observateur :
-
TB
=
tB2
-
tB1
-
Fréquence fB perçue par l'observateur
-

-
La fréquence perçue
par l’observateur est supérieure à la fréquence du phénomène.
-
Le son des bits est
plus aigu.
e)-
Nom de ce phénomène
correspondant à ce décalage de fréquence.
-
C’est
ce que l’on appelle l’effet Doppler.
-
L'effet Doppler fut
présenté par Christian Doppler en 1842 pour les ondes sonores puis par Hippolyte
Fizeau pour les ondes électromagnétiques en 1848.
-
Quelques
applications :
-
Il y a aujourd'hui de
multiples applications.
-
Un radar de contrôle
routier est un instrument servant à mesurer la vitesse des véhicules circulant
sur la voie publique à l'aide d'ondes radar.
-
Les fréquences des
ondes radar sont comprises entre 300 MHz et 15 GHz.
-
Le radar émet une onde
continue qui est réfléchie par toute cible se trouvant dans la direction
pointée.
-
Par effet Doppler,
cette onde réfléchie possède une fréquence légèrement différente de celle émise
:
-
plus grande fréquence
pour les véhicules s'approchant du radar et plus petite pour ceux s'en
éloignant.
-
En mesurant la différence de
fréquence entre l’onde émise et celle réfléchie, on peut calculer la vitesse de
la «cible».
-
Mais les radars
Doppler sont utilisés dans d'autres domaines…
-
En
météorologie,
le radar Doppler permet d'analyser la vitesse et le mouvement des perturbations
et de fournir des prévisions de grêle, de pluies abondantes, de neige ou de
tempêtes.
-
En
imagerie médicale,
le radar Doppler permet d'étudier le mouvement des fluides biologiques.
-
Une sonde émet des
ondes ultrasonores et ce sont les globules rouges qui font office d'obstacles et
les réfléchissent.
-
L'analyse de la
variation de la fréquence des ondes réfléchies reçues par cette même sonde
permet ainsi de déterminer la vitesse du sang dans les vaisseaux.

IV- Exercice :
Atténuation par absorption..
1)- Énoncé.
Lorsqu'on part assister à un concert, il est préférable
de ne pas oublier ses protections acoustiques pour se protéger de niveaux
sonores trop élevés surtout si le concert a lieu dans une salle car on peut
difficilement s'éloigner de la source sonore.
Il en existe plusieurs types représentés ci-dessous :
-
Les bouchons en mousse
(en jaunes)
-
Les casques (en rouge)
-
Les bouchons linéaires
moulés (en bleu)
-
Les bouchons moulés
avec filtre incorporé (en vert) permettant de choisir son atténuation 9, 15 , 25
dB …
►
Représentations :




►
Graphes : A = f
(f)
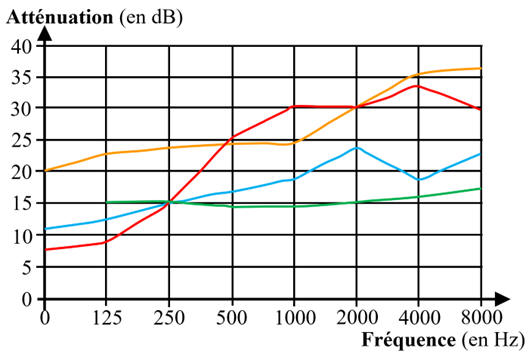
Le graphe ci-dessus indique l'atténuation
A en dB, de
chacune de ces protections, en fonction de la fréquence
f en Hz de la source sonore.
a)-
Indiquer s'il s'agit d'une
atténuation géométrique ou d'une atténuation par absorption.
b)-
Déterminer la fréquence pour
laquelle 3 des 4 protections produisent la même atténuation.
c)-
Expliquer pourquoi le casque
est la pire des protections à utiliser quand on va à un concert.
d)-
Justifier qu'il faut préférer
les bouchons avec filtre incorporé en choisissant correctement le filtre.

2)- Correction.
a)-
Atténuation géométrique ou
atténuation par absorption.
►
L’atténuation
géométrique A :
-
C’est la diminution,
du niveau d’intensité sonore, en décibel (dB) lorsque la distance à la source
sonore augmente.
|
A
= Lproche – Léloigné
|
A :
Atténuation géométrique en décibel (dB)
|
|
Lproche : Niveau d’intensité sonore proche de
la source sonore en décibel (dB)
|
|
Léloigné : Niveau d’intensité sonore éloigné de
la source sonore en décibel (dB)
|
-
Schéma :

-
L’intensité sonore et
le niveau d’intensité sonore diminuent lorsque l’on s’éloigne de la source
sonore.
-
Lorsque la distance à
la source est multipliée par deux l’intensité sonore est divisée par 4 et le
niveau d’intensité sonore diminue de 6 dB.
-
L’atténuation
géométrique ne dépend pas de la fréquence du son émis par la source mais
uniquement de la distance de la source sonore au point considéré.
►
Atténuation par
absorption.
-
Lorsqu’une onde sonore
rencontre une paroi, celle-ci peut être :
-
Transmise,
réfléchie
ou absorbée.
-
Schéma :

-
L’atténuation par absorption
A, en décibel, évalue l’efficacité d’un
matériau à lutter contre la transmission de bruit.
|
A
= Lincident – Ltransmis
|
A :
Atténuation géométrique en décibel (dB)
|
|
Lincident : Niveau d’intensité sonore de l’onde
incidente en décibel (dB)
|
|
Ltransmis : Niveau d’intensité sonore de l’onde
transmise en décibel (dB)
|
-
L’atténuation par
absorption d’un son par un matériau dépend principalement :
-
De la nature du
matériaux (porosité, densité, épaisseur, composition, …)
-
De la fréquence du
son :
-
LeLes matériaux poreux
sont généralement plus efficaces pour absorber les hautes fréquences.
-
Les basses fréquences
nécessitent des matériaux plus épais ou des dispositifs spécifiques (comme les
panneaux résonants) pour être absorbées efficacement.
-
Coefficient d'absorption
acoustique :
-
Pour
quantifier l'absorption d'un matériau, on utilise le coefficient d'absorption
acoustique (α).
- Ce coefficient varie entre
0 (réflexion totale) et 1 (absorption totale) et dépend de la fréquence du son.
-
L'absorption d'un son
par un matériau est un phénomène complexe qui dépend de nombreux facteurs.
-
Pour optimiser
l'acoustique d'un espace, il est essentiel de choisir les matériaux adaptés en
fonction des fréquences à atténuer et des conditions spécifiques du lieu.
►
En résumé :
-
L'absorption
acoustique d'une paroi dépend de plusieurs facteurs :
-
La masse et la
rigidité de la paroi
-
La fréquence de l'onde
acoustique
-
Les caractéristiques
physiques du matériau
-
La nature du matériau
-
L'épaisseur de la
paroi.
-
Analyse
du graphe :

-
Dans le
cas présent, on est en présence d’une
atténuation par absorption.
-
Le graphe donne
l’atténuation en fonction de la fréquence de la source sonore.
-
A
= f
(f).
-
L’L’atténuation du son
émis par la source sonore dépend de sa fréquence.
-
L’atténuation géométrique
ne dépend pas de la fréquence du son émis par la source mais uniquement de la
distance de la source sonore au point considéré.
b)-
Fréquence pour laquelle 3 des
4 protections produisent la même atténuation.
-
Lecture graphique :

-
C’est
pour la fréquence f = = 250 Hz que 3 des 4
protections produisent la même atténuation par absorption (environ 15 dB)
-
Les bouchons en mousse
(en jaunes) produisent
une atténuation par absorption de 24 dB environ.
c)-
Le casque est la pire des
protections à utiliser quand on va à un concert.
-
Pour le casque, on
remarque que l’atténuation du son n’est pas la même pour toutes les fréquences.
-
L’atténuation est plus
importante pour les fréquences élevées.
-
Pour les fréquences
supérieures à 1000 Hz, l’atténuation est supérieure ou égale à 30 dB.
-
Alors que pour les
fréquences inférieures à 250 Hz, l’atténuation est inférieure à 15 dB.
-
PoPour qu’un système de
protection soit efficace, il faut que l’atténuation soit identique ceci quelle
que soit la fréquence du signal.
-
Ainsi le son du
concert sera atténué, mais pas déformé.
d)-
Utilisation des bouchons avec
filtre incorporé en choisissant correctement le filtre.
-
Les bouchons moulés
avec filtre incorporé constituent la meilleure protection pour écouter un
concert.

-
Sur le graphe, on
remarque que la courbe verte varie peu en fonction de la fréquence du signal
sonore (la courbe est pratiquement horizontale).
-
Dans ce cas, il suffit
de choisir la bonne atténuation.

V- Exercice :
Le cor des Alpes.
1)- Énoncé.
Chaque année, au mois de juillet, se
déroule le festival international du cor des Alpes à Haute Nendaz, en Suisse.
Cet instrument folklorique était jadis utilisé par les
bergers pour communiquer entre eux.

DOC. 1 Un instrument à vent : le cor des Alpes
Lorsque l’on souffle dans un cor des Alpes pour la
première fois, il semble impossible d'en sortir un son harmonieux.
Mais avec un peu de pratique, on peut apprendre à
produire jusqu'à 22 notes, ceci sans utiliser ni valve ni bouton.
La gamme de notes réalisable sur cet instrument dépend
d'abord de sa géométrie, puis du talent de celui qui en joue.
Les premiers cors des Alpes (XIVe
siècle) étaient traditionnellement utilisés par les gardiens de troupeaux pour
communiquer entre eux sur des distances d'une dizaine de kilomètres.
Cet instrument de la famille des cuivres est fait d'une
seule pièce de bois, un tube recourbé à son extrémité et mesurant en général de
2 à 4 m de long.
Pour en jouer, le musicien souffle dans une embouchure.
La note la plus grave est atteinte lorsque la longueur
d'onde de l'onde sonore associée à la note est égale à 2 fois la longueur du
cor.
DOC. 2
Seuil d'audibilité humaine en fonction de la fréquences
Le graphique suivant indique les valeurs minimales de
niveau d'intensité sonore audible en fonction de la fréquence.

DOC. 3
Carte topologique de la région

DONNÉES :
-
Intensité sonore de
référence :
I0 = 1,0 ×
10–12 W. m–2 (seuil d’audibilité)
-
Valeur de la célérité
du son dans l’air en fonction de la température
|
Température (en
° C)
|
10
|
20
|
30
|
40
|
|
Célérité (en m .
s–1)
|
337
|
343
|
349
|
355
|
-
InIntensité sonore d’une
source isotrope :
-
Pour
une source isotrope (c’est-à-dire émettant la même énergie dans toutes les
directions) de puissance P,
l’intensité sonore
I
au point M
dépend de la distance
d à la source et s’exprime de la façon
suivante :
-
 avec I
en W . m–2 ,
P
en W et d en m.
avec I
en W . m–2 ,
P
en W et d en m.

QUESTIONS
Un berger, situé au sommet d’une colline (point A de la
carte du DOC. 3 ci-dessus) joue la note la plus grave de son cor des Alpes.
Son instrument a une longueur de 3,4 m.
L’atténuation de l’onde par absorption n’est pas prise
en compte.
Le rayonnement de la source est supposé isotrope.
1.
Question préliminaire : Quel
niveau d’intensité sonore minimal permet d’entendre le cor jouant la note la
plus basse ?
2.
Problème : Pourra-t-on
l’entendre à Haute Nendaz si le niveau d’intensité sonore est de 100 dB à un
mètre de l’instrument ?

2)- Correction.
1.
Question préliminaire :
-
Niveau d’intensité
sonore minimal qui permet d’entendre le cor jouant la note la plus basse
-
Note la plus basse :
-
L’instrument a une longueur :
ℓ = 3,4 m :
-
La note la plus grave
est atteinte lorsque la longueur d'onde de l'onde sonore associée à la note est
égale à 2 fois la longueur du cor
-
λ
= 2 ℓ
-
λ
= 2 × 3,4
-
λ
≈ 6,8 m
-
Fréquence du son
fondamental émis par le cor des Alpes :
-
Chaque année, au mois
de juillet, se
déroule le festival international du cor des Alpes à Haute Nendaz, en Suisse
-
On peut considérer que
la température est de l’ordre de 20 ° C.
-
La
vitesse du son dans l’air est
vson =
343 m . s–1
-

►
Remarque :
Le
spectre d'un son
La
perception d'un son
-
Un son complexe est
formé d’une superposition de vibrations sinusoïdales ayant des amplitudes et des
fréquences différentes.
-
En 1822, le
mathématicien français Joseph FOURIER a montré que :
-
Tout
signal périodique de fréquence
f1
peut être décomposé en une somme de signaux sinusoïdaux de fréquences fn
multiples de f1.
-
Avec
fn
= n.f1
et n € N*
-
La
fréquence f1 est appelée
le fondamental.
-
Les
fréquences 2 f1,
3 f1,
…, n.f1
sont appelées harmoniques.
-
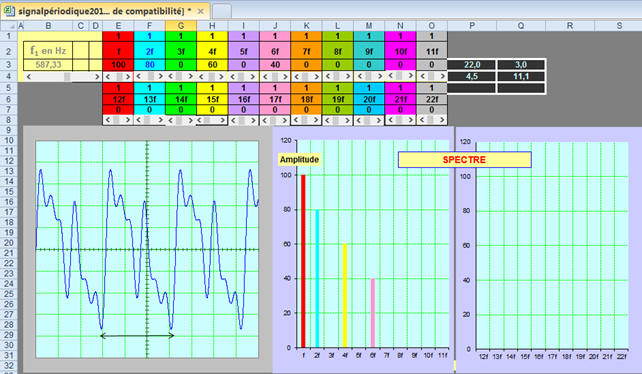
L’analyse spectrale
d’un son permet d’en obtenir le spectre en fréquences.
-
Le spectre en
fréquences d’un son est la représentation graphique de l’amplitude de ses
composantes sinusoïdales en fonction de la fréquence.
-
Exemple :
-
Le son émis par un cor
des Alpes n’est pas un son pur, c’est un son complexe.
-
le cor des Alpes émet
un son fondamental, c'est la fréquence de base qui définit la note jouée.
-
Cette fréquence est
relativement basse,
-
Elle donne au son du
cor des Alpes son caractère grave et puissant.
-
Le son du cor des
Alpes est particulier, car le son fondamental est accompagné de nombreux
harmoniques.
-
Les harmoniques sont
des fréquences multiples du son fondamental,
-
Ceci crée une
superposition de sons qui donne au timbre de l'instrument toute sa richesse et
sa complexité
-
Il peut comporter
plusieurs harmoniques :
-
Le son
fondamental : f1
= 50 Hz,
-
Harmonique de rang 2 : f2
= 2 f1
= 100 Hz,
-
Harmonique
de rang 3 : f3
= 3 f1
= 150 Hz
-
Ainsi de suite.
-
L’amplitude de chaque
harmonique et la présence de certains harmoniques dépendent du timbre de
l’instrument.
Le
cor des Alpes
Le
cor des Alpes : le timbre
2.
Problème :
-
Niveau
d’intensité sonore :
L = 100 dB à
d = 1,0 m de l’instrument
-
Peut-on l’entendre à
Haute Nendaz ?
-
Dans un
premier temps, il faut déterminer la distance
d’
entre la source sonore et Haute Nendaz :
-
Pour ce faire, on
utilise le DOC. 3 qui donne la carte topologique de la région.

-
Tableau :
|
Carte
|
réel
|
|
2,04 cm
|
2,0 km
|
|
8,9 cm
|
d’
|
- 
-
L’atténuation de
l’onde par absorption n’est pas prise en compte.
-
On ne tient compte que
de l’atténuation géométrique.
-
Au cours de la
propagation de l’onde sonore, l’énergie de l’onde sonore se répartit sur une
surface de plus en plus grande (surface d’une sphère).
-
Au cours de la
propagation, sans absorption, de l’onde sonore, la puissance
P de la source se
répartit sur la surface S
d’une sphère centrée sur la source.
-
À la distance
r, la surface de
l’onde : S
= 4 π .
r2 ;
-
l’intensité sonore
I :

►
Fonction réciproque de
la fonction logarithme décimal :
-
 cette relation est
équivalente à :
cette relation est
équivalente à :
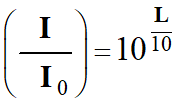
-
Il est possible de
calculer une intensité sonore
I à partir de la connaissance
du niveau d’intensité sonore
L :
-
Relation :
|

|
L :
Niveau d’intensité sonore en décibel (dB)
|
|
I :
Intensité du signal en watt par mètre carré (W. m–2)
|
|
I0
= 1,0
x 10–12 W. m–2 (seuil
d’audibilité) aussi
Intensité
sonore de référence
|
-
On peut
calculer l’intensité sonore
I du cor des Alpes à 1,0 m de la
source :
-
Sachant
que : L = 100 dB
-
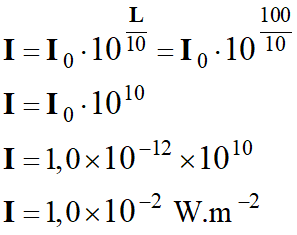
-
Puissance sonore du
signal initial :
-

-
Intensité sonore I’ à la distance
d’
de la source :
-

-
Application
numérique :
-

-
Niveau
d’intensité sonore L’ :
-

►
Autre méthode avec
moins de calculs littéraux :
-
Intensité sonore I du cor des Alpes à 1,0 m de
la source :
-
Sachant
que le niveau d’intensité sonore est :
L
= 100 dB
-
Intensité sonore I’ de la source à la distance
d’
= 8,7 km
-
Dans ce
cas, le niveau d’intensité sonore est
L’.
-

-
D’autre
part, à la distance d du cor des Alpes :
-

-
À la
distance d’ :
-

-
La
source étant isotrope elle émet la même énergie, la même puissance
P
dans toutes les directions :
-
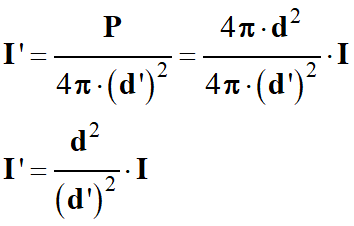
-

-
On
utilise la propriété de la fonction log : log (a
. b) = log
a
+ log b
-

-
Autre
propriété : log a2
= 2 log
a :
-

-
Or :

-

-
Application
numérique :
-

-
Pour savoir si le son
est audible, il faut exploiter le DOC. 2 :

-
À
la fréquence f
= 50 Hz, le son est audible si son niveau d’intensité
sonore L
≥ 46 dB.
-
Dans le
cas présent, le son n’est perçu qu’avec un niveau d’intensité sonore
L’
= 21 dB.
-
En conséquence ce son
n’est pas audible à Haute Nendaz.
-
Les
premiers cors des Alpes (XIVe
siècle) étaient traditionnellement utilisés par les gardiens de troupeaux pour
communiquer entre eux sur des distances d'une dizaine de kilomètres.
-
Comment expliquer
ceci ?
-
Le son émis par un cor
des Alpes est un son complexe.
-
On
remarque que les harmoniques de rang
n
≥ 3 pourrait être perçus.

-
Mais un niveau
d’intensité sonore de 21 dB est un niveau faible qui peut être masqué par le
bruit ambiant.

VI- Exercice :
Déterminer la vitesse d’un hélicoptère par effet Doppler.
1)- Énoncé.
Très pratiques pour porter secours
ou déposer du matériel en terrain accidenté, les hélicoptères peuvent également
se déplacer à des vitesses dépassant les 250 km . h–1.
Avec un niveau d'intensité sonore de 99 dB à proximité
immédiate, ils sont moins bruyants qu'ils ne l'étaient il y a quelques dizaines
d'années.
DOCUMENT : Représentations des fronts de l'onde sonore
émise par l'hélicoptère à un instant donné.


Les portions de cercle des figures 1. et 2. représentent
les fronts de l'onde sonore (Maxima de l’élongation) émise par un hélicoptère à
un instant donné.
Le point P
représente l'hélicoptère.
Dans le cas de la figure 1. l'hélicoptère est immobile.
Dans le cas de la figure 2., il se déplace à la
vitesse de valeur vS
constante le long de (OA)
et vers l'observateur placé au point O.
Les mouvements sont étudiés dans le référentiel
terrestre.
DONNÉE : Fréquence de l’onde émise par
l’hélicoptère : f0
= 8,0 × 102 Hz
QUESTIONS :
1.
Question préliminaire :
a)-
Déterminer, avec précision,
les longueurs d'onde λ0
et λ’
de l'onde sonore reçue par l'observateur lorsque l'hélicoptère est
respectivement immobile, puis en mouvement rectiligne uniforme.
b)-
En déduire une estimation de
la célérité v
de l'onde sonore. Commenter la valeur obtenue.
2.
Exploitation :
a)-
À partir des résultats
obtenus aux deux questions précédentes, calculer la fréquence
f’ de l'onde
sonore reçue par l'observateur lorsque l'hélicoptère est en mouvement.
b)-
Préciser si le son reçu par
l'observateur est plus aigu ou plus grave que celui qu’entend le pilote.
3.
Étude des fronts d’onde :
dans le DOCUMENT, les fronts d'onde, notés F
et G, ont
été émis respectivement aux dates t
et t’.
a)-
Établir l'expression du
décalage Doppler de la longueur d'onde :
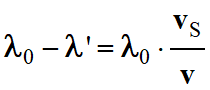
b)-
En déduire la valeur de la
vitesse de l'hélicoptère et déterminer si le résultat obtenu est compatible avec
l'information concernant la vitesse d'un hélicoptère donnée dans le texte
d'introduction de l'exercice.
4.
Un niveau d'intensité sonore
L = 66 dB
est mesuré lorsque l'hélicoptère se trouve à une distance
d = 300 m de
l'observateur. La source sonore (hélicoptère) est supposée isotrope (pas de
direction d’émission privilégiée) et l’atténuation par absorption n'est pas
prise en considération.
a)-
Déterminer le niveau
d'intensité sonore lorsque l'appareil est à 50 m au-dessus de l'observateur.
b)-
Nommer le type d'atténuation
qui explique que le niveau d'intensité sonore est plus faible à 300 m de
l'hélicoptère qu'à 50 m.

2)- Correction.
1.
Question préliminaire :
a)-
Détermination, des longueurs
d'onde λ0
et λ’.
-
λ0 :
longueur d’onde de l'onde sonore reçue par l'observateur lorsque l'hélicoptère
est immobile :
-
Exploitation de la figure 1
-
La longueur d’onde
λ
est la distance parcourue par l’onde en une période
T :
-
Pour plus de
précision, on utilise les fronts d’onde les plus éloignés.
-
Mesures :
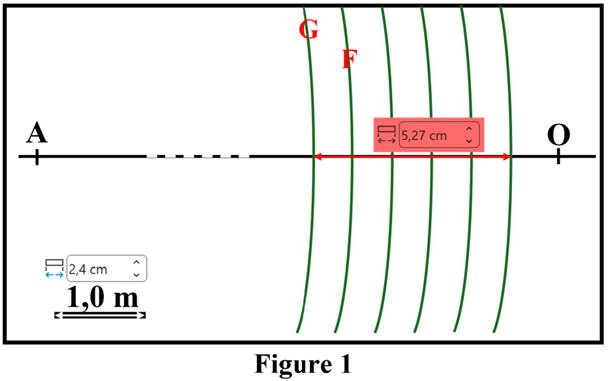
|
Document
|
réel
|
|
2,40 cm
|
1,0 m
|
|
5,27 cm
|
5 λ0
|
-

-
λ’ :
longueur d’onde de l'onde sonore reçue par l'observateur lorsque l'hélicoptère
est en mouvement rectiligne uniforme (il se déplace vers l’observateur)
-
Exploitation de la figure 2
-
Mesures :

|
Document
|
réel
|
|
2,40 cm
|
1,0 m
|
|
4,42 cm
|
5 λ’
|
-

b)-
Estimation de la célérité
v de l'onde
sonore.
-
Relation
fondamentale : λ =
v
. T
-
Avec :

-
Dans le cas présent :
-
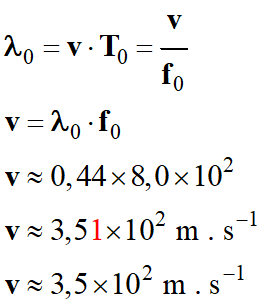
-
Commentaire sur la
valeur obtenue :
-
Ce résultat est
convenable vu la précision des différentes mesures.
-
D’autre part, la
vitesse du son dans l’air dépend beaucoup de la température.
-
Relation donnant la
vitesse du son dans l’air en fonction de la température :
-
 avec
T
température absolue
avec
T
température absolue
-

-
Avec :
vth0 =
331,45 m . s-1.
-
Valeur de la célérité
du son dans l’air en fonction de la température (pour quelques températures)
|
Température (en °
C)
|
10
|
20
|
30
|
40
|
|
Célérité (en m .
s–1)
|
337
|
343
|
349
|
355
|
Mesure de la célérité d'un son dans l'air
2.
Exploitation :
a)-
Fréquence
f’ de l'onde
sonore reçue par l'observateur lorsque l'hélicoptère est en mouvement.
-
On connaît la longueur
d’onde λ’ de
l'onde sonore reçue par l'observateur lorsque l'hélicoptère est en mouvement
rectiligne uniforme (il se déplace vers l’observateur)
-
λ’ ≈
0,37 m
-
On
connait la vitesse v du son dans l’air :
-
v
≈ 3,5 × 102 m . s-1
-
À partir de la
relation fondamentale, on détermine la valeur de la fréquence de l’onde sonore
reçue par l’observateur :
-
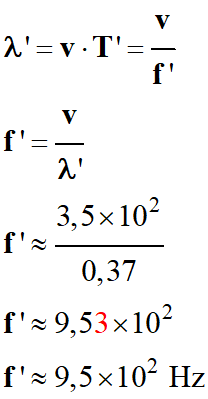
b)-
Nature du son reçu par
l'observateur.
-
En
conséquence f’ >
f :
-
Le son perçu par
l’observateur est plus aigu que celui reçu par le pilote.
3.
Étude des fronts d’onde :
a)-
Expression du décalage
Doppler
-
Analyse du
DOCUMENT :
-
Les
fronts d'onde, notés F et
G,
ont été émis respectivement aux dates
t
et t’
►
L’hélicoptère est
immobile :
-
La
durée qui sépare les dates
t et
t’ correspond à une période de
l’onde sonore.
-
t’
– t
= T0
-
Or
pendant une période T0,
l’onde sonore parcourt une distance correspondante à sa longueur d’onde
λ0.

-
On peut écrire la
relation suivante :
-
λ0
= v
. T0
= v
.( t’
– t)
►
L’hélicoptère se
déplace à la vitesse vS.

-
On remarque que les
fronts d’onde sont plus resserrés.
-
Pendant
la durée T0,
la source (l’hélicoptère) s’est rapprochée de l’observateur de la distance :
-
ℓ
= vS. T0
-
Les
trains d’onde se sont rapprochés de la distance
ℓ.
-
λ’
= λ0
– ℓ
-
λ’
= λ0
– vS. T0
-
λ0
– λ’
= vS. T0
-
avec :
λ0 =
v
. T0
-
On en déduit
l’expression du décalage Doppler :
-
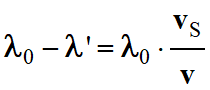
b)-
Valeur de la vitesse de
l'hélicoptère
-

-
Application
numérique :
-

-
Vitesse
de l’hélicoptère en km . h–1
-

-
Les
hélicoptères peuvent également se déplacer à des vitesses dépassant les 250 km .
h–1.
-
Le résultat obtenu est
compatible avec l'information concernant la vitesse d'un hélicoptère donnée dans
le texte d'introduction de l'exercice.
4.
Atténuation sonore :
a)-
Niveau d'intensité sonore
lorsque l'appareil est à 50 m au-dessus de l'observateur.
-
Un
niveau d'intensité sonore
L = 66 dB est mesuré lorsque
l'hélicoptère se trouve à une distance
d = 300 m
de l'observateur.
-
La source sonore
(hélicoptère) est supposée isotrope (pas de direction d’émission privilégiée) et
l’atténuation par absorption n'est pas prise en considération.
►
Intensité sonore d’une
source isotrope :
-
Pour
une source isotrope (c’est-à-dire émettant la même énergie dans toutes les
directions) de puissance P, l’intensité sonore
I
au point M
dépend de la distance
d à la source et s’exprime de la façon
suivante :
-
 avec
I
en W . m–2 ,
P
en W et d
en m.
avec
I
en W . m–2 ,
P
en W et d
en m.

-
Expression du niveau
d’intensité sonore : L
-
Relation
mathématique :
|

|
L :
Niveau d’intensité sonore en décibel (dB)
|
|
I :
Intensité du signal en watt par mètre carré (W. m–2)
|
|
I0
= 1,0
× 10–12 W. m–2 (seuil
d’audibilité)
|
-
Un
niveau d'intensité sonore
L = 66 dB est mesuré lorsque
l'hélicoptère se trouve à une distance
d = 300 m
de l'observateur.
-
En conséquence :
-

-
On note
L’
le niveau d’intensité sonore de l’appareil lorsqu’il est à la distance
d’
= 50 m :
-

-
La
source étant isotrope elle émet la même énergie, la même puissance
P
dans toutes les directions :
-
Intensité sonore I à la distance
d de la source
-

-
Intensité sonore I’ à la distance
d’
de la source :
-

- On tire l'expression suivante :
-

-
En utilisant les
propriétés de la fonction logarithme et le fait que :

-

-
Application
numérique :
-

b)-
Type d'atténuation qui
explique que le niveau d'intensité sonore est plus faible à 300 m de
l'hélicoptère qu'à 50 m.
-
Il s’agit de
l’atténuation géométrique :
-
L’atténuation de
l’onde par absorption n’est pas prise en compte.
-
On ne tient compte que
de l’atténuation géométrique.
-
Au cours de la
propagation de l’onde sonore, l’énergie de l’onde sonore se répartit sur une
surface de plus en plus grande (surface d’une sphère).
-
Au cours de la
propagation, sans absorption, de l’onde sonore, la puissance
P de la source se
répartit sur la surface S
d’une sphère centrée sur la source.
-
À la distance
r, la surface de
l’onde : S
= 4 π .
r2 ;
-
l’intensité sonore
I :

►
L’atténuation
géométrique A :
-
C’est la diminution,
du niveau d’intensité sonore, en décibel (dB) lorsque la distance à la source
sonore augmente.
|
A
= Lproche – Léloigné
|
A :
Atténuation géométrique en décibel (dB)
|
|
Lproche : Niveau d’intensité sonore proche de
la source sonore en décibel (dB)
|
|
Léloigné : Niveau d’intensité sonore éloigné de
la source sonore en décibel (dB)
|
-
Schéma :

-
L’intensité sonore et
le niveau d’intensité sonore diminuent lorsque l’on s’éloigne de la source
sonore.
-
Lorsque la distance à
la source est multipliée par deux l’intensité sonore est divisée par 4 et le
niveau d’intensité sonore diminue de 6 dB.
-
L’atténuation
géométrique ne dépend pas de la fréquence du son émis par la source mais
uniquement de la distance de la source sonore au point considéré.