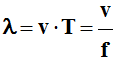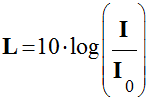|
Chap. N° 02 |
Caractéristiques des ondes. Cours. |
|
|
|
|
III- Caractéristiques des
ondes sonores et ultrasonores. |
|
IV- Application |
|
|
|
a)- Exercice 6 page 50. Connaître
les ondes progressives. b)- Exercice 7 page 50. Déterminer
une vitesse de propagation c)- Exercice 11 page 51. Exploiter
une expérience. d)- Exercice 12 page 51. Connaître
la double périodicité. e)- Exercice 16 page 52. Exploiter
des spectres sonores. f)- Exercice 19 page 52. Incertitude
sur la mesure. g)- Exercice 26 page 54. À chacun
son rythme. h)- Exercice 29 page 55. Accorder
une guitare avec un diapason. i)- Exercice 34 page 58. L’oreille
humaine en concert. |
- On fait tomber un objet dans l’eau et on enregistre le mouvement observé.
- On observe le
déplacement d’une ride circulaire.
- Le milieu de propagation de la perturbation est le plan d’eau ; c’est un milieu à deux dimensions.
- La perturbation se
déplace dans toutes les directions à partir du point source S.
- Un point de la surface de l’eau s’élève lors du passage de la perturbation et reprend sa position initiale.
- On est en
présence d’une onde transversale.
-
On fait tomber une goutte d’eau et on observe la
propagation du déplacement d’une ridule circulaire à partir du
point d’impact de la goutte.
b)- Compression des spires d’un ressort :
- Un ressort est tendu horizontalement.
- On comprime quelques spires à une extrémité, puis on lâche brusquement.
- On observe le déplacement
de la compression le long du ressort.
-
Le milieu de propagation est unidimensionnel, la
direction de propagation est l’axe du ressort.
- Une spire du ressort se déplace parallèlement à l’axe du ressort et reprend sa position d’équilibre après le passage de la perturbation.
- On est en présence d’une onde longitudinale.
- Propagation de la perturbation :
-
On observe le
déplacement de la perturbation, ici une zone où les spires du
ressort sont plus resserrées (zone compressée).
c)-
Propagation d’une perturbation le long d’une corde :
-
On soumet une corde horizontale à une brusque secousse
verticale.
-
On observe le déplacement de la perturbation le long de
la corde.
-
Le milieu de propagation est unidimensionnel, la
direction de propagation est la corde.
-
La perturbation se déplace le long de la corde sans
transport de matière.
-
La déformation a lieu perpendiculairement à la direction
de propagation.
-
On est en présence d’une onde transversale.
-
Le phénomène de propagation d’une perturbation dans un
milieu est appelé onde progressive.
-
Une onde progressive correspond au déplacement d’une
perturbation dans un milieu.
►
Remarque :
-
Certaines ondes ont besoin d’un milieu matériel pour se
propager, ce sont les ondes mécaniques.
-
D’autres n’ont pas besoin d’un milieu matériel pour se
propager, ce sont les ondes électromagnétiques.
-
Une onde progressive qui se propage dans une seule
direction est appelée onde progressive à une dimension.
-
La corde, le ressort et l’eau constituent des milieux
matériels.
-
Dans chaque cas, on crée une perturbation et on observe
le déplacement d’une onde mécanique progressive.
-
Une perturbation correspond à la variation d’une
propriété mécanique des points d’un milieu matériel.
- Une onde mécanique correspond à la propagation d’une perturbation dans un milieu matériel sans transport de matière.
- C’est pour cela que l’on dit qu’un mobile se déplace alors
qu’une onde se propage.
-
La propagation de l’onde mécanique peut se faire dans des
milieux à une, deux ou trois dimensions.
-
La direction dans laquelle se propage la perturbation est
la direction de propagation de l’onde.
- Après le passage de la perturbation, chaque point du milieu matériel reprend sa position initiale.
- On dit que le
milieu matériel est élastique.
-
Onde longitudinale :
|
-
Onde longitudinale : - La direction de déplacement temporaire de la matière et la direction de propagation de l'onde sont les mêmes. -
On parle
aussi d'ondes de compression : elles créent de proche en proche des ondes de compression - détente du milieu de
propagation. -
Elles vibrent parallèlement à leur direction de
propagation (cas du ressort) |
-
Onde transversale :
|
-
Onde transversale : -
Une onde est transversale lorsque la déformation du
milieu de matériel a lieu perpendiculairement à la direction de
propagation de la perturbation. -
C’est le cas de la corde : la direction de propagation de
l’onde est celle de la corde (horizontale) et la déformation de
la corde a lieu perpendiculairement à la corde. -
La direction de déplacement temporaire de la matière et
la direction de
propagation de l'onde sont perpendiculaires.
- On parle aussi d'ondes de cisaillement. - Elles vibrent
perpendiculairement à leur direction de propagation (cas de la
corde) |
-
La célérité d’une onde mécanique dépend du milieu de
propagation.
-
C’est une caractéristique du milieu de propagation.
-
Elle ne dépend pas de l’amplitude de la déformation.
-
La célérité est le quotient de la distance parcourue sur
la durée de parcours.
-

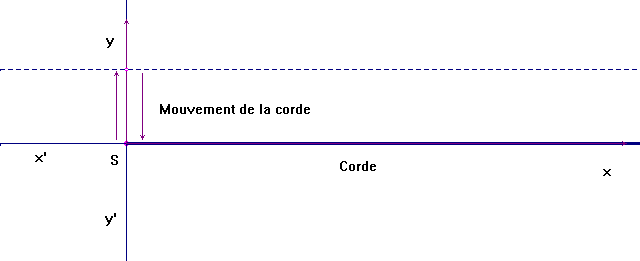
4)- Notion de retard et
d’élongation.
a)-
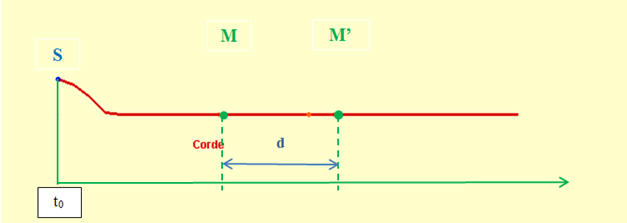
Mise en évidence du retard :
-
On considère la propagation d’une perturbation le long
d’une corde horizontale.
-
Dans un premier temps, on crée la perturbation au point
S de la corde.
-
La source S monte pendant la durée
Δt1
puis redescend pendant la durée Δt2.
-
Le mouvement de S est un mouvement rectiligne
vertical.
-
On repère la direction de propagation de l’onde à l’aide
de l’axe (x’x) et on repère la position de la source
S
grâce à l’axe (y’y).
-
La perturbation, créée au point
S de la corde au
temps t0, se propage de proche en proche.
-
Elle atteint le point
M, puis le point
M’
du milieu matériel.
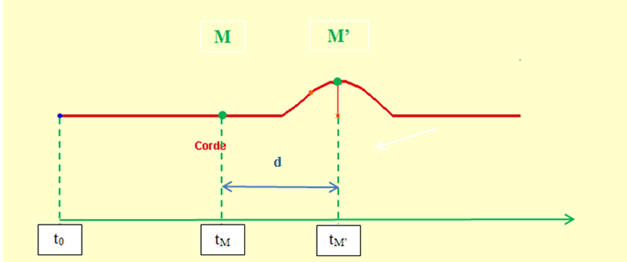
-
Chaque point du milieu matériel reproduit la perturbation
de la source S (on suppose que la perturbation se propage
sans amortissement).
-
La perturbation au point
M reproduit la
perturbation de la source S avec un retard
τ, car
la perturbation met un certain temps pour progresser de
S
à M.
-
Le retard τ
est la durée mise par l’onde pour se
propager de S à
M :
-
En conséquence, si
v est la célérité de l’onde et
SM la distance parcourue par l’onde :
-

-
Si on repère chaque point de la corde par son abscisse
x, la source
S est située à l’origine des abscisses :
-
L’abscisse du point
M est notée :
xM.
-
Le mouvement d’un point
M situé à la distance
xM
de la source est le même que celui de la source avec un retard :
-

-
La courbe représentant le mouvement de
M en
fonction du temps est la même que celle de la source décalée de
la durée τ.
-
Si yS
(t), représente la position de la
source au cours du temps, le mouvement de
M est
yM
(t),
-
Avec : yM (t) =
yS
(t –
τ) car l’onde se propage de
S vers
M.
►
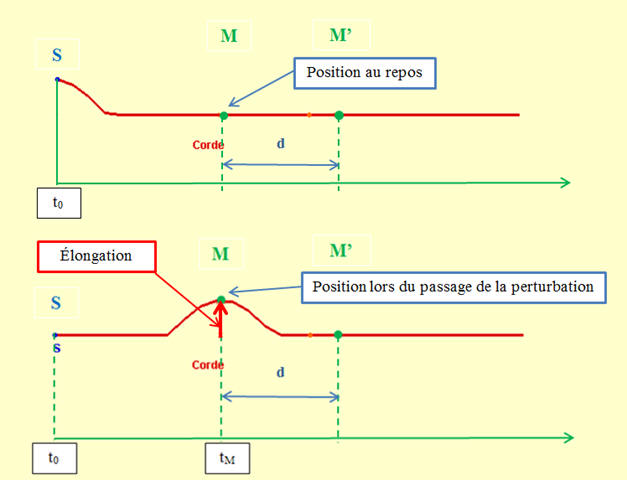
Élongation lors d’un passage d’une perturbation :
-
On appelle élongation d’un point du milieu matériel, la
position, qu’il occupe lors du passage de la perturbation, par
rapport à sa position au repos.
-
On crée une onde mécanique progressive sur une corde en
produisant, à son extrémité S, une perturbation très
brève à l’instant t = 0 s.
-
L’onde se propage sur la corde avec la célérité
v
=
►
Le point M situé à
-
Chaque point de la corde reproduit la perturbation créée
en S avec un retard
τ.
- L’onde se propage du point S (la source) vers le point M.
- Pour le point
M situé à la distance
SM
=
-
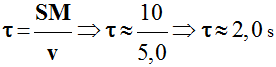
-
Le point M effectue un mouvement à la date
t
= t0 +
τ, en conséquence à la date
t
= 2,0 s.
-
Comme la durée de la perturbation est brève, on peut
considérer que le point M n’est plus en mouvement à la
date t = 2,5 s.
►
Même question pour le point
N placé à
- L’onde se propage du point S (la source) vers le point N.
- Pour le point
N situé à la distance
SN
=
-
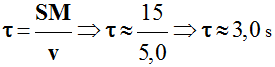
-
Le point N effectue un mouvement à la date
t
= t0 +
τ,
c'est-à-dire à la date
t
= 3,0 s.
-
En conséquence, à la date
t = 2,5 s, la
perturbation n’a pas atteint le point N.
-
Il n’est pas en mouvement.
c)-
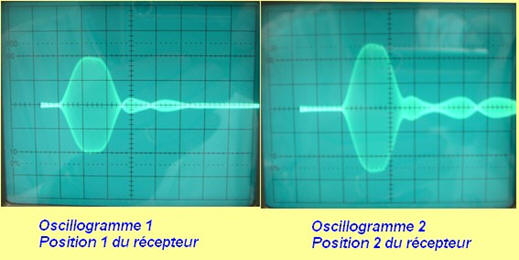
Exemple 2 : Mesure d’un retard à l’oscilloscope.
- On observe l’écran de l’oscilloscope lorsque l’émetteur est en mode salve
- Une salve ultrasonore est une perturbation sonore de fréquence supérieure à 20 kHz séparée par une durée réglable.
-
Lorsque le récepteur est en position 1 (graduation zéro)
on observe l’oscillogramme 1.
-
Lorsque le récepteur est en position 2, on observe
l’oscillogramme 2.
-
Position 2 :

-
On donne les réglages de l’oscilloscope :
![]() Grâce à la durée de balayage de l’oscilloscope,
déduire la valeur du retard τ.
Grâce à la durée de balayage de l’oscilloscope,
déduire la valeur du retard τ.
-
Retard mesuré à l’aide de l’oscilloscope :
-
Δt =
τ =
s . x
-
Δt =
τ ≈ 0,500
× 1,00
-
Δt =
τ ≈ 0,500 ms
-
Δt =
τ ≈ 5,00
× 10 – 4 s
II-
Onde progressive périodique.
a)-
Onde progressive périodique :
|
-
Définition : - Une onde progressive est périodique si la perturbation qu’elle engendre se reproduit de manière identique à intervalles
de temps égaux, appelés période, notée
T. -
La période T des oscillations est la durée d’une
oscillation complète. -
Cette durée s’exprime en seconde s. -
La fréquence f
du phénomène représente le nombre
de période par seconde. -
C’est l’inverse de la période
T. -
-
La fréquence f s’exprime en hertz : Hz. |
b)-
Onde progressive sinusoïdale :
-
Une onde progressive est sinusoïdale lorsque l’élongation
de tout point du milieu de propagation est une fonction
sinusoïdale du temps.
-
Une onde progressive sinusoïdale est périodique.
-
La période T des oscillations est la durée d’une
oscillation complète.
![]() Visualisation d’une onde ultrasonore à l’écran
d’un oscilloscope :
Visualisation d’une onde ultrasonore à l’écran
d’un oscilloscope :
|
L’émetteur (émetteur d’onde ultrasonore) est relié à la voie
YA de l’oscilloscope Le récepteur est relié à la
voie YB de l’oscilloscope |
|
Oscillogramme d’une tension périodique sinusoïdale de période
T. |
c)-
Formulation mathématique de l’onde mécanique
sinusoïdale :
-
L’évolution de l’élongation,
x (t), au
cours du temps est donnée par une fonction de la forme
suivante :
-
x (t) =
Xmax
. cos (2π /
T + Ф)
|
|
x (t) est
l’élongation au temps t |
|
Xmax est
l’amplitude de la perturbation |
|
|
Ф est la phase à l’origine des
dates en radian (rad) |
|
|
|
-
Une onde progressive est sinusoïdale lorsque l’élongation
de tout point du milieu de propagation est une fonction
sinusoïdale du temps.
-
On est en présence d’une onde progressive périodique.
►
Mise en évidence :
-
À l’extrémité S
de la lame d’un vibreur, on
attache une corde élastique, puis on met le vibreur en
mouvement.
-
La perturbation périodique se propage le long de la corde
jusqu’au point B.
-
On place du coton au point
B pour amortir le
phénomène et éviter la réflexion de l’onde.
-
Une onde progressive périodique se propage le long de la
corde.
-
Cette onde possède une périodicité temporelle
T.
-
On peut étudier le mouvement de chaque point de la corde
de deux façons :
-
On peut effectuer un enregistrement vidéo et faire une
observation au ralenti.
-
On peut effectuer une observation stroboscopique.
- Un stroboscope est un appareil qui délivre des éclairs très brefs à intervalle de temps régulier réglable.
- Il permet
d’immobiliser le phénomène et de l’observer au ralenti.
- On éclaire la corde avec un stroboscope et on règle la fréquence des éclairs du stroboscope afin d’observer une corde immobile.
- Si on augmente légèrement la fréquence des éclairs, on
peut observer le mouvement au ralenti d’un point marqué d’un
repère.
-
Lorsque la corde est immobile, tous les points de la
corde effectuent entre deux éclairs consécutifs une ou plusieurs
oscillations complètes.
-
En conséquence, tous les points de la corde vibrent avec
la même fréquence que la source et tous les points de la corde
effectuent le même mouvement que la source.
- L’onde progressive possède une périodicité temporelle.
- La
source et chaque point de la corde atteint par l’onde vibrent
avec la même période T.
-
Animation :
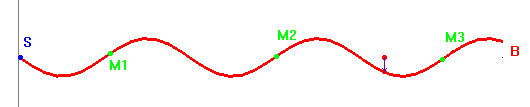
- On utilise l’éclairage stroboscopique et on immobilise la corde.
- Certains points M1,
M2,
M3… ont exactement le même mouvement à chaque
instant.
-
Ils sont dans le même état physique.
-
Ils passent à leur position d’équilibre ou à leur
écartement maximal aux mêmes instants.
- On dit que les points M1, M2, M3. …vibrent en phase.
- Ils sont dans le même
état vibratoire.
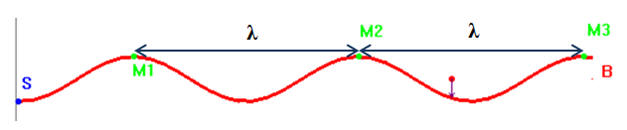
-
La distance qui sépare les points M1
et M2 d’une part,
M2 et
M3
d’autre part est la même.
-
C’est une grandeur caractéristique de l’onde.
-
On l’appelle la longueur d’onde, notée
λ, elle
s’exprime en mètre (m).
3)- Définition de la longueur d’onde
-
La longueur d’onde
λ est la distance séparant deux
points consécutifs du milieu qui vibrent en phase.
-
En conséquence : deux points séparés par une distance
d multiple de la longueur d’onde vibrent en phase.
-
Si d est la distance qui sépare deux points qui
vibrent en phase alors : d
= k.
λ avec
k
Î
N*
-
Il découle de ceci que pendant la durée d’une période
T, l’onde parcourt la distance
d égale à la longueur
d’onde λ.
-
Si v
représente la célérité de l’onde, on peut
écrire la relation liant ces différentes grandeurs.
|
λ
= v.T |
La longueur d’onde λ en
mètre (m) |
|
La célérité de l’onde v
en (m / s) |
|
|
La période T en seconde
(s) |
-
La longueur d’onde
λ est la distance parcourue par
l’onde pendant une période T.
-
Une onde progressive périodique possède une double
périodicité.
-
Une périodicité temporelle
T est une périodicité
spatiale λ.
►
Autre écriture :
-
Comme la fréquence est l’inverse de la période, on peut
écrire la relation fondamentale sous une autre forme :
|
|
La longueur d’onde λ en
mètre (m) |
|
La célérité de l’onde v
en (m / s) |
|
|
La période T en seconde
(s) |
|
|
La fréquence f en hertz
(Hz) |
III- Caractéristiques des ondes sonores et ultrasonores.
1)- Perception des ondes sonores.
-
L’oreille humaine normale perçoit les ondes sonores dont
les fréquences sont comprises entre 20 Hz et 20 kHz.
-
Les ondes sonores de fréquences
f < 20 Hz sont
appelées infrasons.
-
Les ondes sonores de fréquences
f > 20 kHz sont
appelées ultrasons.
![]()
a)-
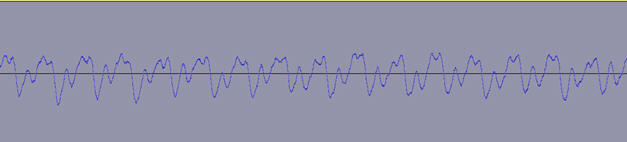
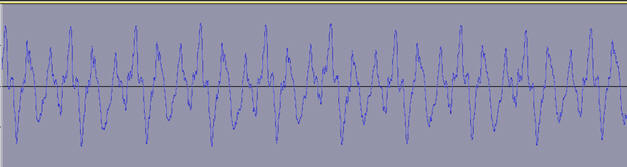
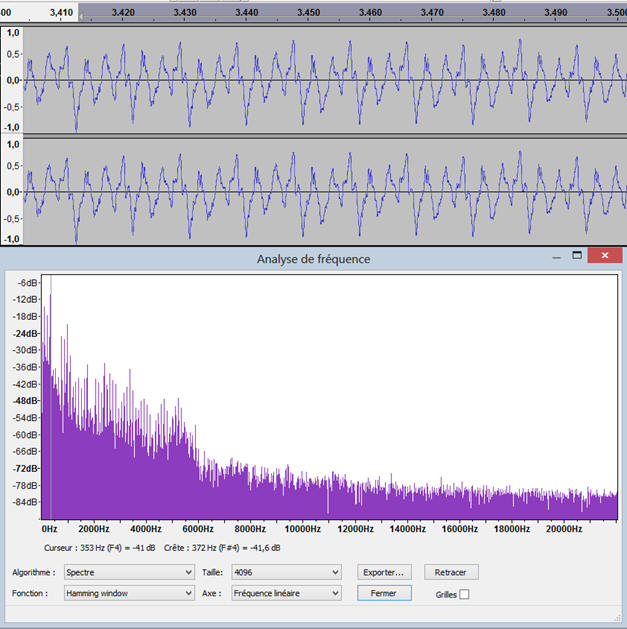
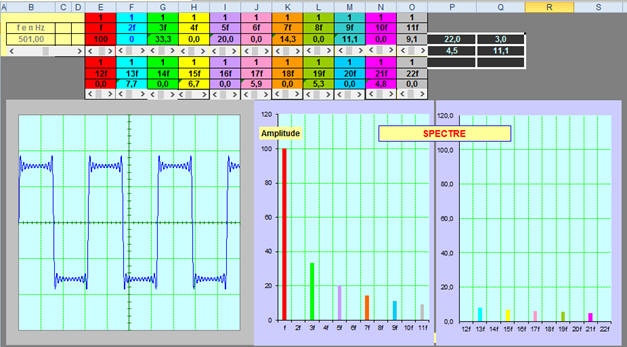
Exemple : Son produit par une guitare.
-
Le spectre d’un son produit par une guitare est
périodique, mais n’est pas sinusoïdal.
-
La guitare émet un son complexe alors que le
GBF produit
un signal pur, un signal sinusoïdal.
-
Enregistrement réalisé avec le logiciel Gratuit
AUDACITY
Son clair : essai02
Son distordu : essai03
b)-
Spectre en fréquences
-
Un son complexe est formé d’une superposition de
vibrations sinusoïdales ayant des amplitudes et des fréquences
différentes.
-
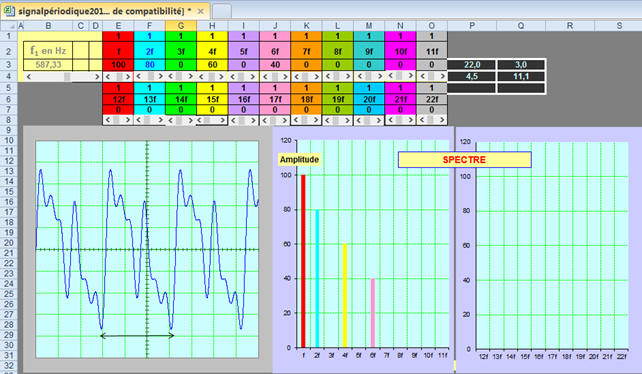
En 1822, le mathématicien français Joseph FOURIER a
montré que :
-
Tout signal périodique de fréquence
f1
peut être décomposé en une somme de signaux sinusoïdaux de
fréquences fn multiples de
f1.
-
Avec fn =
n.f1
et n
Î
N*
-
La fréquence f1
est appelée le
fondamental.
-
Les fréquences 2 f1, 3 f1,
…, n.f1
sont appelées
harmoniques.
-
L’analyse spectrale d’un son permet d’en obtenir le
spectre en fréquences.
-
Le spectre en fréquences d’un son est la représentation
graphique de l’amplitude de ses composantes sinusoïdales en
fonction de la fréquence.
►
Cas du son distordu :
-
Le spectre en fréquences du son distordu émis par une
guitare montre plusieurs pics de fréquences :
-
f1
≈ 587 Hz. C’est la fréquence du
fondamental, le ré3.
-
2 f1, la première
harmonique,
puis, 2 f1 et 6
f1.
c)-
La hauteur et le timbre.
-
La hauteur d’un son :
-
Plus la fréquence d’un son est faible et plus le son est
grave ou bas.
-
Plus la fréquence d’un son est élevée et plus le son est
aigu ou haut.
-
Le timbre d’un son :
-
Le timbre d’un son dépend du nombre et de l’amplitude des
harmoniques qui sont présents.
-
Deux sons de même hauteur émis par des instruments
différents ne sont pas perçus de la même manière, car les
harmoniques, associées au fondamental, sont différentes.
-
L’analyse spectrale d’un son musical permet de
caractériser :
-
La hauteur du son est liée à la fréquence
f1du
fondamental
-
Le timbre du son est lié au nombre et à l’amplitude des
harmoniques présentes.
-
Analyse de la fréquence réalisée avec le logiciel
AUDACITY :
d)-
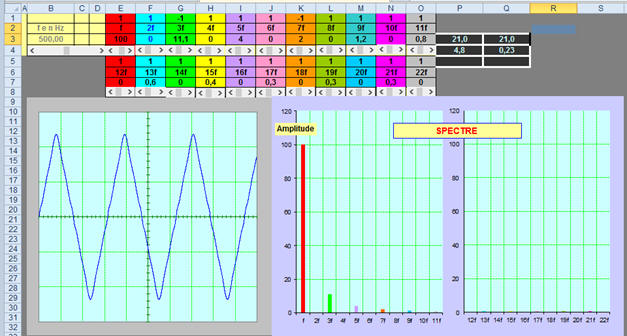
Signaux délivrés par un GBF relié à un haut-parleur : :
-
Le signal triangulaire :
-
Le signal « carré » :
3)- Le niveau d’intensité sonore.
-
L’intensité sonore, notée
I, caractérise
l’intensité du signal reçue par l’oreille.
-
Elle s’exprime en watt par mètre carré : W / m2
ou W. m–2
-
L’oreille humaine normale perçoit les signaux sonores
dont l’intensité est comprise entre
-
Une valeur minimale
I0 = 1,0
× 10–12 W. m–2 (seuil d’audibilité)
-
Et une valeur maximale
Imax = 25 W. m–2
(seuil de douleur).
- Comme l’écart entre ces deux valeurs est très grand, on a créé une nouvelle grandeur, qui utilise une échelle logarithmique :
- appelée le niveau d’intensité sonore, notée L.
-
Relation mathématique :
|
|
Le niveau d’intensité sonore
L s’exprime en décibel (dB) |
|
I caractérise
l’intensité du signal en W. m–2 |
|
|
I0 = 1,0
× 10–12 W. m–2
(seuil d’audibilité) |
-
La notation log fait référence à la fonction
logarithme décimal.
-
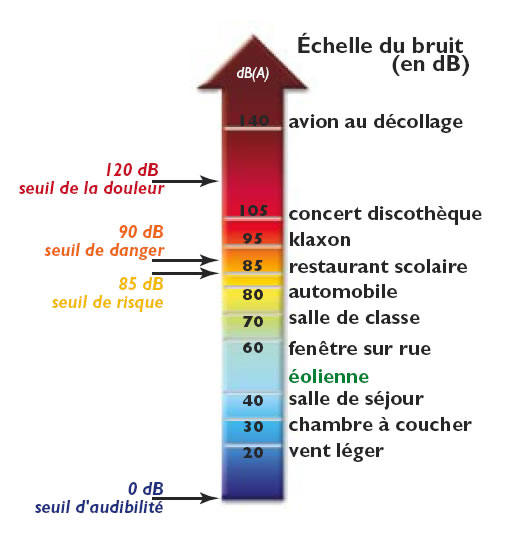
Ainsi, l’échelle de niveau d’intensité sonore
L
varie de 0 dB à environ 140 dB.
-
Alors que l’intensité sonore
I varie de
I0
= 1,0
x 10–12 W. m–2 à 102 W.
m–2
►
Quelques propriétés de la fonction logarithme
décimal :
-
log 1 = 0, log 10 = 1, log 10
n =
n,
log 10 –n
= –n
-
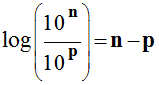
-
![]()
-
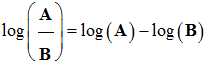
-
Échelle des niveaux d’intensité sonore
L :
►
Remarque :
- Lorsque plusieurs instruments de musique jouent ensemble, les intensités sonores I dues à chaque instrument s’ajoutent,
- alors que les niveaux d’intensité sonore
L ne
s’ajoutent pas.
1)- QCM.
|
|
a)- Exercice 6 page 50. Connaître
les ondes progressives.
b)- Exercice 7 page 50. Déterminer
une vitesse de propagation
c)- Exercice 11 page 51. Exploiter
une expérience.
d)- Exercice 12 page 51. Connaître
la double périodicité.
e)- Exercice 16 page 52. Exploiter
des spectres sonores.
f)- Exercice 19 page 52. Incertitude
sur la mesure.
g)- Exercice 26 page 54. À chacun
son rythme.
h)- Exercice 29 page 55. Accorder
une guitare avec un diapason.
i)- Exercice 34 page 58. L’oreille
humaine en concert.
|
|









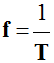


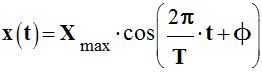
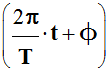 Phase à l’instant t en radian (rad)
Phase à l’instant t en radian (rad)