Chap. N° 09 Exercices 2024 : Forcer l'évolution d'un système chimique.

	Demi-équation électronique
Première étape : On écrit le couple oxydant / réducteur	CO₂ (g) C₆H₁₂O₆ (aq)
Deuxième étape : On équilibre le carbone	6 CO₂ (g) C₆H₁₂O₆ (aq)
Troisième étape : On équilibre l’élément oxygène avec de l’eau	6 CO₂ (g) C₆H₁₂O₆ (aq) + 6 H₂O (ℓ)
Quatrième étape : On équilibre l’élément hydrogène avec H⁺ (on travaille en milieu acide)	6 CO₂ (g) + 24 H⁺ (aq) C₆H₁₂O₆ (aq) + 6 H₂O (ℓ)
Cinquième étape : On équilibre les charges avec les électrons.	6 CO₂ (g) + 24 H⁺ (aq) + 24 e ^– C₆H₁₂O₆ (aq) + 6 H₂O (ℓ)

- Couple oxydant / réducteur : Chap. N° 02 Réactions d’oxydo-réduction Cours Première (2019)

- O₂ (g) / H₂O (ℓ).

	Demi-équation électronique
Première étape : On écrit le couple oxydant / réducteur	O₂ (g) H₂O (ℓ)
Deuxième étape : On équilibre l’élément oxygène avec de l’eau	O₂ (g) 2 H₂O (ℓ)
Troisième étape : On équilibre l’élément hydrogène avec H⁺ (on travaille en milieu acide)	O₂ (g) + 4 H⁺ (aq) 2 H₂O (ℓ)
Quatrième étape : On équilibre les charges avec les électrons.	O₂ (g) + 4 H⁺ (aq) + 4 e ^– 2 H₂O (ℓ)

b)- Équation de la réaction modélisant la photosynthèse.

6 CO₂ (g) + 24 H⁺ (aq) + 24 e ^– C₆H₁₂O₆ (aq) + 6 H₂O (ℓ)	×1
2 H₂O (ℓ) O₂ (g) + 4 H⁺ (aq) + 4 e ^–	× 6
6 CO₂ (g) + 6 H₂O (ℓ) C₆H₁₂O₆ (aq) + 6 O₂ (g)

c)- Indiquer la source énergétique utilisée par les végétaux pour forcer cette transformation.

- Le système chimique lors de la photosynthèse évolue en sens opposé à celui donné par le critère d'évolution spontanée.

- Le système a besoin d’un apport d’énergie pour évoluer dans le sens inverse.

- C’est le Soleil qui apporte cette énergie.

- La photosynthèse :

- Les plantes, par la photosynthèse, assurent la conversion de l’énergie rayonnante de la lumière en énergie chimique.

- Elles forment un réacteur chimique.

- Une partie des radiations de la lumière du Soleil est absorbée par la chlorophylle contenue dans les feuilles.

- Cette énergie permet la réaction entre le dioxyde de carbone atmosphérique et l’eau.

- Il se forme alors du dioxygène et du glucose.

Déterminer un type de conversion.

Les organismes chlorophylliens

II- Exercice : Compteur électrique d’Edison.

1)- Énoncé.

Entre 1882 et 1895, les habitations étaient alimentées en courant électrique continu.

Le scientifique américain Thomas Edison (1847-1931) a mis en place un appareil permettant de mesurer « l'électricité consommée » :

10 % du courant de chaque habitation était dérivé vers une cellule électrolytique dont une des électrodes en zinc plongeait dans une solution de sulfate de zinc {Zn²⁺ (aq) + SO₄^2– (aq)}.

Une fois par mois, l’électrode était débranchée, rincée séchée puis pesée.

Lors d’un relevé pour une maison, après une durée de consommation électrique Δt = 30 jours, une masse m = 34 g de zinc avait été déposée sur l'électrode.

DONNÉES :

Masse molaire du zinc : M (Zn) = 65,4 g . mol^–1.

a)- Exprimer puis calculer la quantité de matière de zinc n (Zn) déposée pendant ces 30 jours.

b)- Exprimer puis calculer la charge électrique totale Q ayant circulé dans la cellule pendant cette même durée. Exprimer en A . h.

c)- Exprimer puis calculer la consommation d’électricité en A . h de la maison considérée.

d)- Proposer un moyen permettant d'éviter de réalimenter la cellule électrolytique en ions Zn²⁺ tous les mois.

2)- Correction.

a)- Expression et calcul de la quantité de matière de zinc n (Zn) déposée pendant ces 30 jours.

- Étude de l’électrolyse de la solution de sulfate de zinc II :

- Plus de 50% de la production mondiale de zinc sont obtenus par électrolyse d'une solution de sulfate de zinc acidifiée à l'acide sulfurique.

- Les ions sulfate ne participent pas aux réactions électrochimiques.

- On observe un dépôt métallique sur l'une des électrodes et un dégagement gazeux sur l'autre.

- Dans le cas présent, on utilise une électrode en zinc et une électrode de graphite.

- On veut que le dépôt de zinc se fasse sur l’électrode de zinc.

► Réactions susceptibles de se produire sur chaque électrode

- Couples oxydant / réducteur :

- Zn²⁺ (aq) / Zn (s) ; H⁺ (aq) / H₂ (g) ; O₂ (g) / H₂O (ℓ)

- À la cathode se produit une réduction (borne reliée à la borne négative du générateur).

- Deux réactions sont possibles :

- H⁺ (aq) + 2 e^– = H₂ (g)

- Zn²⁺ (aq) + 2 e^– = Zn (s)

- À l’anode se produit une oxydation :

- 2 H₂O (ℓ) = O₂ (g) + 4 e^– + 4 H⁺ (aq)

- Équation bilan :

Zn²⁺ (aq) + 2 e^–		Zn (s)	× 2
2 H₂O (ℓ)		O₂ (g) + 4 e^– + 4 H⁺ (aq)	× 1
2 Zn²⁺ (aq) + 2 H₂O (ℓ)	→	2 Zn (s) + O₂ (g) + 4 H⁺ (aq)

- Cette transformation chimique est une transformation forcée.

- C’est le générateur qui apporte l’énergie nécessaire à la transformation chimique.

- Schéma du dispositif :

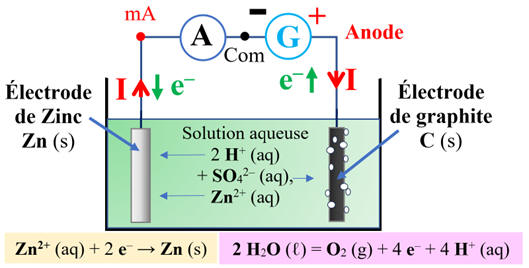
Schéma du dispositif d'électrolyse

- Les électrons arrivent par la borne – du générateur.

- Les électrons se déplacent dans le circuit électrique et les ions dans la solution aqueuse.

- Les anions chargés négativement se déplace vers l'anode reliée à la borne positive du générateur.

- Les cations chargés positivement se déplace vers la borne négative du générateur.

► Remarque :

- Les termes anode et cathode pour noter les électrodes s’emploient aussi pour les piles.

- L’anode désigne toujours l’électrode où se produit l’oxydation.

- La cathode désigne toujours l’électrode où se produit la réduction

- Durée de consommation électrique :

- Δt = 30 jours

- Masse de zinc : m = 34 g et masse molaire : M (Zn) = 65,4 g . mol^–1

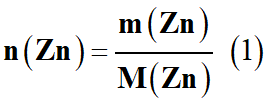
- n (Zn) = m (Zn) / M (Zn)

- Application numérique :

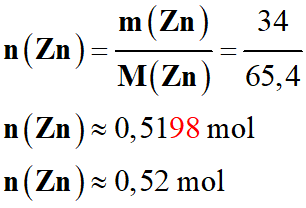
- n (Zn) = 0,52 mol

b)- Expression et calcul de la charge électrique totale Q ayant circulé dans la cellule pendant la durée Δt = 30 jours.

- Charge électrique totale Q :

- La quantité d’électricité Q mise en jeu au cours de l’électrolyse pendant la durée Δt :

Q = n (e^–) . F
Q	Quantité d’électricité mise en jeu (C)
n (e^–)	Quantité de matière d’électrons échangés (mol)
F	Constante de Faraday : F = 96500 C . mol^–1

- Constante de Faraday : La valeur absolue de la charge d’une mole d’électrons définit le faraday de symbole F.

- 1 F = |N_A . n (e^–)|

- Q quantité d’électricité mise en jeu : grandeur positive : Unité : coulomb (C).

- Quantité de matière d’électrons échangés : n (e^–)

- On utilise la demi-équation électronique qui fait intervenir les électrons et l’élément zinc :

Équation

Zn²⁺ (aq)

+ 2 e^–

→

Zn (s)

Quantité

de matière

n (Zn²⁺)

n (e^–)

n (Zn)

Coefficient

stœchiométrique

- Relation :

- n (e^–) = 2 n (Zn)

- On en déduit la relation suivante :

- Q = n (e^–) . F

- Q = 2 n (Zn) . F

- Application numérique :

- Q = 2 n (Zn) . F

- Q ≈ 2 × 0,52 × 96500

- Q ≈ 1,00 ×10⁵ C

- Q ≈ 1,0 ×10⁵ C

- De la relation :

Q = I . Δt
I	Intensité du courant (A)
Q	Quantité d’électricité mise en jeu (C)
Δt	Durée de fonctionnement de l’électrolyseur (s)

- On tire que :

- 1C = 1 A . s = 1/3600 A . h

- En A . h :

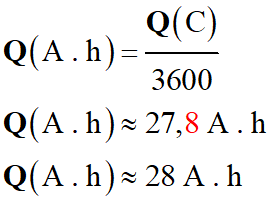
- Q (A.h) = 28 A . h

c)- Expression et calcul de la consommation d’électricité en A . h de la maison considérée.

- Le scientifique américain Thomas Edison (1847-193)1 a mis en place un appareil permettant de mesurer « l'électricité consommée » :

- 10 % du courant de chaque habitation était dérivé vers une cellule électrolytique.

- La quantité d’électricité calculée précédemment représente 10 % de « l’électricité consommée » par la maison :

- Q_consommée = 10 Q (A . h)

- Application numérique :

- Q_consommée = 10 Q (A . h)

- Q_consommée ≈ 10 × 28

- Q_consommée ≈ 2,8 × 10² A . h

d)- Moyen permettant d'éviter de réalimenter la cellule électrolytique en ions Zn²⁺ tous les mois.

- Le mieux est d’utiliser un compteur Linky qui prélève moins de 10 % de « l’électricité consommée ».

électrolyse d'une solution d'iodure de zinc.

III- Exercice : Rails de chemin de fer :

1)- Énoncé.

La préparation du manganèse métallique, utilisé pour la fabrication des rails de chemin de fer, se fait par électrolyse d'une solution de sulfate de manganèse II {Mn²⁺ (aq) + SO₄^2– (aq)} acidifiée par du sulfate d’ammonium{2 NH₄⁺ (aq) + SO₄^2– (aq)}.

DONNÉES :

- Couples oxydant / réducteur :

- H⁺ (aq) / H₂ (g)

- Mn²⁺ (aq) / Mn (s)

- S₂O₈^2– (aq) / SO₄^2– (aq)

- O₂ (g) / H₂O (ℓ).

- Masse molaire : M (Mn) = 54,9 g . mol^–1.

1. Expliquer pourquoi le sulfate d'ammonium permet acidifier la solution.

2. Dresser la liste des espèces chimiques présentes en solution afin de prévoir toutes les réactions électrochimiques susceptibles de se produire aux électrodes.

3. En opérant sous une tension de U = 5,0 V, pour une intensité I = 35,0 kA, seul du manganèse se forme et un dégagement de dioxygène est observé.

a)- Écrire l'équation de la réaction modélisant l'électrolyse.

b)- Exprimer puis calculer la masse maximale m_max de métal qu'il est possible d'obtenir chaque jour.

c)- En réalité, la masse de métal obtenu est m_exp = 530 kg. Interpréter cette constatation expérimentale et calculer le rendement de la synthèse du manganèse.

d)- Exprimer puis calculer la consommation massique, c'est-à-dire l'énergie nécessaire pour déposer un kilogramme de manganèse.

2)- Correction.

1. Acidification de la solution.

- Sulfate d'ammonium : {2 NH₄⁺ (aq) + SO₄^2– (aq)}

- L’ion sulfate ne possède pas de propriétés acido-basiques (base conjuguée d’un acide fort)

- L’ion ammonium possède des propriétés acido-basiques.

- C’est la forme acide du couple : NH₄⁺ (aq) / NH₃ (aq) : K_A = 6,3 × 10^–¹⁰

- C’est un acide faible :

NH₄⁺(aq) + H₂O (ℓ) NH₃ (aq) + H₃O⁺(aq)

- Cette solution permet d’acidifier la solution et d’améliorer la conduction de la solution.

2. Liste des espèces chimiques présentes en solution.

- Les différentes solutions : sulfate de manganèse, sulfate d’ammonium,

- Mn²⁺ (aq), SO₄^2– (aq)

- NH₄⁺ (aq), NH₃ (aq)

- Le solvant l’eau : H₂O (ℓ)

- H₃O⁺(aq) ou H⁺(aq) et HO^– (aq) (ultra minoritaire)

- Prévision des réactions électrochimiques susceptibles de se produire aux électrodes :

- Réactions susceptibles de se produire à la cathode : (réduction)

- Mn²⁺ (aq) + 2 e^– Mn (s)

- 2 H⁺ (aq) + 2 e^– H₂ (g)

- Réactions susceptibles de se produire à l’anode : (oxydation)

- 2 SO₄^2– (aq) S₂O₈^2– (aq) + 2 e^–

- 2 H₂O (ℓ) O₂ (g) + 4 H⁺(aq) + 4 e^–

3. Électrolyse :

a)- Équation de la réaction modélisant l'électrolyse.

- Avec les réglages du générateur : du manganèse Mn (s) se forme et un dégagement de dioxygène O₂ (g) est observé.

Mn²⁺ (aq) + 2 e^–		Mn (s)	× 2
2 H₂O (ℓ)		O₂ (g) + 4 e^– + 4 H⁺ (aq)	× 1
2 Mn²⁺ (aq) + 2 H₂O (ℓ)	→	2 Mn (s) + O₂ (g) + 4 H⁺ (aq)

b)- Expression et calcul de la masse maximale m_max de métal qu'il est possible d'obtenir chaque jour.

- Tension : U = 5,0 V,

- Intensité : I = 35,0 kA,

- Durée : Δt = 1,0 j = 8,64 × 10⁴ s

- Calcul de la quantité d’électricité Q mise en jeux :

- L’intensité I du courant qui circule dans l’électrolyseur pendant la durée Δt est donnée par la relation suivante :

Q = I . Δt
I	Intensité du courant (A)
Q	Quantité d’électricité mise en jeu (C)
Δt	Durée de fonctionnement de l’électrolyseur (s)

- La quantité d’électricité Q mise en jeu au cours de l’électrolyse pendant la durée Δt :

Q = n (e^–) . F
Q	Quantité d’électricité mise en jeu (C)
n (e^–)	Quantité de matière d’électrons échangés (mol)
F	Constante de Faraday : F = 96500 C . mol^–1

- Constante de Faraday : La valeur absolue de la charge d’une mole d’électrons définit le faraday de symbole F.

- 1 F = |N_A . n (e^–)|

- Q quantité d’électricité mise en jeu : grandeur positive : Unité : coulomb (C).

- On peut déduire de ces relations la quantité de matière d’électrons échangés au cours de l'électrolyse :

- quantité de matière d’électrons échangés

- Pour relier cette quantité de matière d’électrons échangés à la quantité de matière de manganèse formé, il faut utiliser la demi-équation électronique suivante :

Équation

Mn²⁺ (aq)

+ 2 e^–

→

Mn (s)

Quantité

de matière

n (Mn²⁺)

n (e^–)

n_max (Mn)

Coefficient

stœchiométrique

- Relation :

- n (e^–) = 2 n_max (Mn)

- n max

- Et enfin, en utilisant la relation suivante :

- m_max = m_max (Mn) = n_max (Mn) . M (Mn)

- Application numérique :

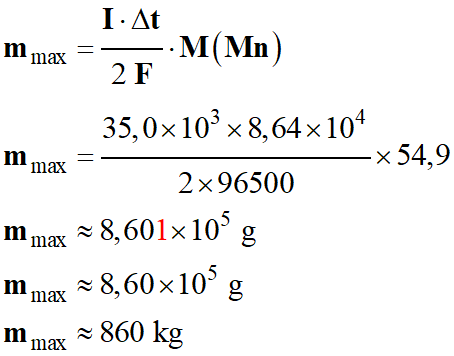
- m max = 860 kg

c)- Rendement de la synthèse du manganèse.

- Bilan énergétique d’un électrolyseur.

Bilan énergétique d’un électrolyseur

- Dans une pile ou un électrolyseur, une partie de l’énergie est dissipée sous forme de transfert thermique (effet joule).

- Ce phénomène diminue le rendement de ces convertisseurs.

- En conséquence la masse de métal obtenu m_exp est toujours inférieure à la valeur m_max calculée précédemment

- Masse calculée précédemment : m_max = 860 kg

- Masse de métal obtenu : m_exp = 530 kg.

- Rendement de l’électrolyse :

- Rendement de l’électrolyse

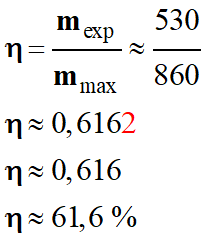
d)- Consommation massique.

- Énergie nécessaire pour déposer un kilogramme de manganèse :

- Énergie électrique nécessaire pour produire m_exp = 530 kg de manganèse :

- W_elec = U . I . Δt

- Tension : U = 5,0 V,

- Intensité : I = 35,0 kA,

- Durée : Δt = 1,0 j = 8,64 × 10⁴ s

- Pour déposer un kilogramme de manganèse :

- Consommation massique E_mas :

- Consommation massique Emas

- Pour les unités : [W_elec] = (V) . (A) . (s) = (J)

- 1 kWh = 3,6 × 10⁶ J

- Le joule (J) étant une unité très petite, on peut exprimer l'énergie électrique consommée en kWh :

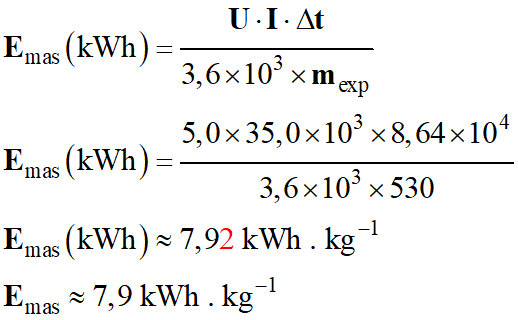
- Consommation massique Emas = 7,9 kWh / kg

VI- Exercice : Constante de Faraday :

1)- Énoncé.

électrolyse de l'iodure de potassium

La constante de Faraday correspond à la charge électrique d’une mole de charge élémentaire.

Cette constante peut être déterminée expérimentalement par une expérience d'électrolyse.

L’électrolyse d'une solution d'iodure de potassium est réalisée dans un tube en U.

L’électrolyse est maintenue pendant une durée Δt = 10 min et le générateur extérieur délivre un courant d'intensité constante I = 10 mA.

À l'issue de cette électrolyse le contenu du tube en U est versé dans un bécher.

Les électrodes et le tube sont rincés et les eaux de rinçage sont ajoutées dans le bécher.

Le diiode formé est alors titré par une solution de thiosulfate de sodium{2 Na⁺ (aq) + S₂O₃^2– (aq)} de concentration en quantité de matière C’ = 10 mmol . L^–1.

Le volume versé à l'équivalence V_éq vaut 6,1 mL.

DONNÉES :

- Couples oxydant / réducteur

- I₂ (aq) / I^– (aq)

- K⁺ (aq) / K (s)

- H₂O (ℓ) / H₂ (g)

- O₂ (g) / H₂O (ℓ).

- S₄O₆^2– (aq) / S₂O₃^2– (aq)

a)- Déterminer l'équation de la réaction d'électrolyse.

b)- Déterminer l'équation de la réaction support du titrage.

c)- À partir de la valeur du volume à l'équivalence obtenu, déterminer la quantité de diiode titré.

d)- En déduire la valeur de la constante de Faraday.

e)- Comparer à la valeur donnée dans les tables. Discuter des sources d'erreurs possibles.

2)- Correction.

a)- Équation de la réaction d'électrolyse.

- Électrolyse d'une solution d'iodure de potassium :

- Espèces présentes : K⁺ (aq) + I^– (aq)

- Le solvant : H₂O (ℓ)

- Les couples oxydant / réducteur :

- I₂ (aq) / I^– (aq)

- K⁺ (aq) / K (s)

- H₂O (ℓ) / H₂ (g)

- O₂ (g) / H₂O (ℓ).

- Réactions susceptibles de se produire à la cathode : (réduction)

- K⁺ (aq) + e^– K (s)

- 2 H₂O (ℓ) + 2 e^– H₂ (g) + 2 HO^– (aq)

- Réactions susceptibles de se produire à l’anode : (oxydation)

- 2 H₂O (ℓ) O₂ (g) + 4 H⁺(aq) + 4 e^–

- 2 I^– (aq) I₂ (aq) + 2 e^–

► Remarques :

- Le potassium K (s) est un métal très réactif.

- Il réagit avec l'eau pour former de l'hydroxyde de potassium (K⁺ (aq) + HO^– (aq)) et un dégagement de dihydrogène gazeux (H₂ (g)).

- Cette réaction est exothermique et peut être dangereuse.

- Potassium métal dans l’eau :

- On laisse tomber un petit morceau de potassium dans un bécher contenant de l'eau :

- il s'enflamme spntanémment et se déplace à la surface de l'eau (coloration violette caractéristique de l'élément potassium Couleur de flamme)

Potassium métal dans l’eau

- Lors de l'électrolyse, l'eau, solvant, est présente et réagit avec le potassium formé.

- À la cathode, on observe un dégagement gazeux de dihydrogène H₂ (g) :

dégagement gazeux de dihydrogène H2 (g)

- À l’anode on note l’apparition d’une coloration brune due à la formation de diiode I₂ (aq).

formation de diiode I2 (aq)

- On peut aussi observer suivant les conditions expérimentales un dégagement gazeux de dioxygène.

- Dans le cas présent, on considère que les réactions aux électrodes sont les suivantes :

2 I^– (aq)	=	I₂ (aq) + 2 e^–	× 1
2 H₂O (ℓ) + 2 e^–	=	H₂ (g) + 2 HO^– (aq)	× 1
2 I^– (aq) + 2 H₂O (ℓ)	→	I₂ (aq) + H₂ (g) + 2 HO^– (aq)

b)- Équation de la réaction support du titrage.

- Titrage de la solution de diiode par une solution de thiosulfate de sodium{2 Na⁺ (aq) + S₂O₃^2– (aq)} de concentration en quantité de matière C’ = 10 mmol . L^–1.

- On est en présence d’un titrage colorimétrique.

- L’équivalence est repérée par un changement de couleur :

- Le diiode I₂ (aq), seule espèce colorée du système chimique étudié, n’est plus présent à l’équivalence.

- La solution devient incolore.

- Toutefois, l’équivalence étant difficile à repérer, on ajoute juste avant l’équivalence un indicateur coloré, l’empois d’amidon, qui permet de repérer plus facilement l’équivalence.

Titrage colorimétrique

► Dispositif expérimental :

- Au départ, la solution a la teinte suivante :

solution de diiode

- On verse progressivement la solution de thiosulfate de sodium (contenue dans la burette graduée) dans l’erlenmeyer, tout en agitant.

- La solution de S₁ de diiode, I₂ (aq) se décolore progressivement.

- Pour que l'indicateur qui permet de repérer l'équivalence soit performant, il faut en verser quelques gouttes juste avant l'équivalence lorsque la solution est jaune paille (on peut faire plusieurs dosages pour améliorer la technique).

- Teinte du mélange réactionnel avant l’ajout de l’empois d’amidon :

solution de diiode

- Après l’ajout de l’empois d’amidon, le mélange réactionnel prend une teinte bleue-violacée.

solution de diiode - empois d'amidon

- À l’équivalence, le mélange réactionnel prend la teinte suivante :

équivalence

- Le volume de solution S de thiosulfate de sodium est alors : V_éq = 6,1 mL

- Schéma du montage :

montage

► Équation de la réaction de titrage :

I₂ (aq) + 2 e^–	=	2 I^– (aq)	× 1
2 S₂O₃^2– (aq)	=	S₄O₆^2– (aq) + 2 e^–	× 1
2 I^– (aq) + 2 S₂O₃^2– (aq)	→	I₂ (aq) + S₄O₆^2– (aq)

I₂ (aq) + 2 S₂O₃^2– (aq) → 2 I^– (aq) + S₄O₆^2– (aq)

c)- Valeur de la quantité de diiode titré.

► Tableau d’avancement de la réaction :

Équation		I₂ (aq) +	2 S₂O₃^2– (aq)	→	2 I^– (aq)	+ S₄O₆^2– (aq)
état	Avanc. x (mol)	n (I₂) (mol)	n (S₂O₃^2–) (mol)		n (I^–) (mol)	n (S₄O₆^2–) (mol)
État initial à l’équivalence (mol)	0	n (I₂) = ?	n (S₂O₃^2–) = C’ . V_éq		0	0
Au cours de la transformation	x	n (I₂) – x	n (S₂O₃^2–) – 2 x		2 x	x
État final à Équivalence	x_max = x_éq	n (I₂) – x_éq	n (S₂O₃^2–) – 2 x_éq		2 x_max	x_max
		0	0
		n (I₂) = x_éq	C’ . V_éq = 2 x_éq		2 x_max	x_max

► Quantité de matière n (I₂) de diiode :

- À l’équivalence, les réactifs ont été mélangés dans les proportions stœchiométriques :

Équation

de titrage

I₂ (aq)

+ 2 S₂O₃^2– (aq)

→

2 I^– (aq) + S₄O₆^2– (aq)

Quantités

de matières

à l’équivalence

n (I₂)

C’ . V_éq

Coefficients

stœchiométriques

- Application numérique :

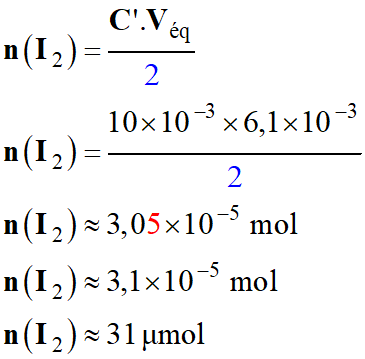
- n (I2) = 3,1 E-5 mol

d)- Valeur de la constante de Faraday.

- Charge électrique totale Q :

- La quantité d’électricité Q mise en jeu au cours de l’électrolyse pendant la durée Δt :

Q = n (e^–) . F
Q	Quantité d’électricité mise en jeu (C)
n (e^–)	Quantité de matière d’électrons échangés (mol)
F	Constante de Faraday : F = 96500 C . mol^–1

- Constante de Faraday : La valeur absolue de la charge d’une mole d’électrons définit le faraday de symbole F.

- 1 F = |N_A . n (e^–)|

- Q quantité d’électricité mise en jeu : grandeur positive : Unité : coulomb (C).

- Quantité de matière d’électrons échangés : n (e^–)

- On utilise la demi-équation électronique qui fait intervenir les électrons et l’élément zinc :

Équation

I₂ (aq)

+ 2 e^–

→

2 I^– (aq)

Quantité

de matière

n (I₂)

n (e^–)

n (I^–)

Coefficient

stœchiométrique

- Relation :

- n (e^–) = 2 n (I₂)

- On en déduit la relation suivante :

- Q = n (e^–) . F

- Q = 2 n (I₂) . F

- D’autre part :

- L’électrolyse est maintenue pendant une durée Δt = 10 min et le générateur extérieur délivre un courant d'intensité constante I = 10 mA.

- Quantité d’électricité Q mise en jeux :

- L’intensité I du courant qui circule dans l’électrolyseur pendant la durée Δt est donnée par la relation suivante :

Q = I . Δt
I	Intensité du courant (A)
Q	Quantité d’électricité mise en jeu (C)
Δt	Durée de fonctionnement de l’électrolyseur (s)

- Q = 2 n (I₂) . F = I . Δt

- On peut en déduire l’expression qui permet de calculer la constante de Faraday F :

- constante de Faraday F

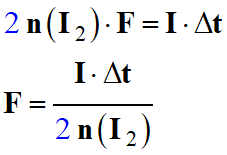
- Application numérique :

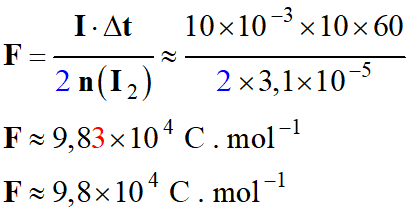
- F = 9,8 E4 C / mol

e)- Comparaison avec la valeur donnée dans les tables.

- Incertitude relative sur la valeur expérimentale de la constante de Faraday F :

- Incertitude relative

- Les deux valeurs sont très proches.

- Le résultat de l’expérience est satisfaisant.

- Les sources d'erreurs possibles :

- Bilan énergétique d’un électrolyseur.

Bilan énergétique d’un électrolyseur

- Dans une un électrolyseur, une partie de l’énergie est dissipée sous forme de transfert thermique (effet joule).

- Ce phénomène diminue le rendement de ces convertisseurs.

- C’est une source d’erreur.

- On est en présence d’un titrage colorimétrique.

- L’équivalence est repérée par un changement de couleur :

- Le diiode I₂ (aq), seule espèce colorée du système chimique étudié, n’est plus présent à l’équivalence.

- La solution devient incolore.

- Toutefois, l’équivalence étant difficile à repérer,

- Pour repérer plus facilement l'équivalence et limiter les erreurs, on ajoute juste avant l’équivalence un indicateur coloré, l’empois d’amidon.

- C’est aussi une cause d’erreur.