|
Caractériser les phénomènes ondulatoires |
|
|
|
|
|
|
QCM N° 16
Caractériser les
phénomènes ondulatoires.
Pour chaque
question, indiquer la (ou les) bonne(s) réponse(s). |
|||||
|
|
Énoncé |
A |
B |
C |
R |
|
1 |
Une onde
mécanique progressive
s’accompagne : |
D’un transport
de matière |
D’un transport
d’énergie |
D’un transport
d’énergie et
d’un transport
de matière |
B |
|
2 |
Une onde de
célérité v passe
en A, puis
en B. Le retard
de l’onde ente
A et B :
|
|
|
|
C |
|
3 |
Une onde met 5,0
s à
parcourir 5,0 m
d’une corde.
Sa célérité
vaut : |
2,5 m . s–1 |
1,0 m . s–1 |
1,0 km . h–1 |
B |
|
4 |
Une onde
sinusoïdale, de
période 2,0 × 10–1
s, a une
longueur d’onde
de 10 m.
Sa célérité est :
|
2,0 × 10–2
m .
s–1 |
2,0 m .
s–1 |
50 m .
s–1 |
C |
|
5 |
Le signal
ci-dessous,
qui se propage
dans
un milieu
homogène : |
Présente une
périodicité
spatiale |
Présente une
périodicité
temporelle |
N’est pas
périodique |
AB |
|
6 |
La fréquence du
signal
ci-dessous vaut :
|
2,0 Hz |
0,5 Hz |
5,0 × 102 Hz |
C |
|
7 |
Un milieu est
parcouru
par une onde de
célérité
v
= 500 m . s–1. Cette onde est
caractérisée par : |
Une période
T
= 1,6× 10–5 s |
Une longueur
d’onde
λ
= 4 mm |
Une longueur
d’onde
λ
= 8 mm |
AC |
|
8 |
À 5,0 m d’un
haut-parleur,
le son émis de
puissance
acoustique égale
à 3,0 W
se disperse sur
une surface
dont l’aire est
proche de
300 m2.
L’intensité sonore
vaut environ :
|
I
= 10–2
W . m–2 |
I
= 0,6
W . m–1 |
I
= 102
m2 . W–1 |
A |
|
9 |
Un observateur
situé à
quelques mètres
d’un
marteau-piqueur
perçoit
un son
d’intensité sonore
I
= 31,6 mW . m–2.
Le
niveau
d’intensité sonore
perçu par
l’observateur
vaut :
Donnée :
Intensité sonore
de référence :
I0
= 10–12
mW . m–2 |
L
= 105 dB |
L
= 3,16 × 1010
dB |
Il manque
des données
pour pouvoir
calculer L |
A |
|
10 |
Trois sons sont
enregistrés
à l’aide d’un
microphone.
Lequel ou
lesquels de ces
sons sont purs ? |
|
|
|
BC |
|
11 |
On analyse le son
émis
par un instrument
de
musique grâce à
un
logiciel
acquisition. |
Le son
est pur |
La fréquence
fondamentale
vaut 700 Hz |
La fréquence
fondamentale
vaut 350 Hz |
C |
|
12 |
La musique
stockée
sur les
plateformes
d’écoute en ligne
est composée :
|
De signaux
analogiques |
De signaux
numériques |
De signaux
analogiques
compressés |
B |
|
13 |
La numérisation
d’un
signal analogique
est
représentée sur
le
graphique
suivant : |
Le signal
analogique
est le signal
continu |
Le signal
analogique
est le signal
discontinu |
Le signal
analogique
est converti
en signal
numérique
grâce à un
convertisseur
CAN |
AC |
QCM réalisé avec le logiciel Questy
Pour s’auto-évaluer
Chap N° 12 Émission et propagation
d’un son (Classe de seconde)
Phys N° 01 Les ondes mécaniques
(cours de la classe de terminale S)
Chap N° 15 Les ondes mécaniques
(Cours de la classe de première)
Chap N° 17 Sons et effet Doppler
Onde mécanique :
-
Une onde mécanique
progressive est le phénomène de propagation d’une perturbation dans un milieu
matériel élastique, sans transport de matière, mais avec transport d’énergie.
-
La position d’un point du
milieu matériel est repérée par son élongation.
-
L’élongation maximale est
appelée amplitude de l’onde.
-
Exemples :
|
|
Célérité d’une onde :
-
On appelle célérité la
vitesse de propagation d’une onde, pour la distinguer de la vitesse de
déplacement d’un objet.
-
La célérité est le quotient
de la distance parcourue sur la durée de parcours.
|
|
La célérité de
l’onde v en (m . s–1) |
|
La distance
parcourue d en mètre (m) |
|
|
La durée du
parcours Δt en seconde (s) |
-
Distance parcourue et durée :
-
Exemple : Propagation d’une
perturbation le long d’une corde.



-
La
perturbation crée au point S de la corde au temps
t0
se propage de proche en proche.
-
Elle atteint
le point A, puis le point
B
du milieu matériel.
-
La
perturbation au point A reproduit la perturbation de
la source S avec un retard
τ1
= tA
– t0, car la
perturbation met un certain temps pour progresser de
S
à A.
-
De même, la
perturbation en un point A
n’arrive pas instantanément au point B
mais avec un retard
-
τ = tB
– tA.
-
L’onde se
propage sur la distance d entre les points
A
et B
alignés dans la direction de propagation.
-
En
conséquence, la perturbation parcourt la distance
d = AB
pendant la durée τ
= tB – tA.
-
![]()
Valeur de la célérité d’une onde :
-
On appelle célérité la
vitesse de propagation d’une onde, pour la distinguer de la vitesse de
déplacement d’un objet.
-
La célérité est le quotient
de la distance parcourue sur la durée de parcours.
|
|
La célérité de
l’onde v en (m . s–1) |
|
La distance
parcourue d en mètre (m) |
|
|
La durée du
parcours Δt en seconde (s) |
-

-
En km . h–1 :
-

Relation
fondamentale (onde sinusoïdale) :
-
Il découle de
ceci que pendant la durée d’une période
T,
l’onde parcourt la distance
d égale à la longueur d’onde
λ.
-
Si
v
représente la célérité de l’onde, on peut écrire la relation
liant ces différentes grandeurs.
|
λ
= v . T |
La longueur
d’onde λ en mètre (m) |
|
La célérité de
l’onde v en (m / s) |
|
|
La période
T en seconde (s) |
-
La longueur
d’onde λ
est la distance parcourue par l’onde pendant une période
T.
-

Onde progressive périodique :
-
Une onde progressive
périodique possède une double périodicité.
-
Une
périodicité temporelle T (période) est une périodicité
spatiale λ (longueur d’onde).
-
La période : durée au bout de
laquelle le phénomène se reproduit identique à lui-même.
-
La longueur d’onde :
distance parcourue par l’onde pendant une période.
La fréquence :
-
La fréquence
f est l’inverse de
la période T
:
-
![]()
-
Dans le cas présent,
T = 2,0 ms
-

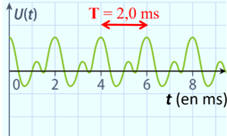
Longueur d’onde :
-
La longueur d’onde
λ d’une onde
progressive périodique est la distance parcourue par l’onde pendant une période
T.
-
Schéma :

-
Exploitation du graphe
S =
f (x)
-
La longueur d’onde :
λ ≈ 8,0 mm
-
Relation fondamentale :
-

Intensité sonore :
-
L’intensité sonore est liée à
l’amplitude du signal sonore.
-
Plus
l’amplitude du signal sonore est élevée plus l’intensité sonore
I
est grande.
-
L’intensité
sonore, notée I, caractérise l’intensité du
signal reçue par l’oreille.
-
L’intensité
sonore I
est la puissance P
par unité de surface
S transportée par une onde sonore.
|
|
I
: Intensité sonore en watt par mètre carré (W . m–2) |
|
P :
Puissance transportée par l’onde sonore en watt (W) |
|
|
S
: Surface de l’onde sonore en mètre carré
(m2) |
-
Elle s’exprime
en watt par mètre carré : W / m2
ou W. m–2
-
L’oreille humaine normale
perçoit les signaux sonores dont l’intensité est comprise entre
-
Une valeur
minimale I0
= 1,0
×
10–12 W. m–2
(seuil d’audibilité)
-
Et une valeur
maximale Imax
= 25 W. m–2 (seuil de
douleur).
-

Niveau d’intensité sonore :
-
On définit le
niveau d’intensité sonore
L à partir de l’intensité associée au
seuil d’audibilité.
-
Relation mathématique :
|
|
L :
Niveau d’intensité sonore en décibel (dB) |
|
I :
Intensité du signal en watt par mètre carré (W. m–2) |
|
|
I0
= 1,0
×10–12
W. m–2 (seuil d’audibilité) |
-
La notation
log
fait référence à la fonction logarithme décimal.
-
Ainsi,
l’échelle de niveau d’intensité sonore
L
varie de 0 dB à environ 140 dB.
-
Alors que
l’intensité sonore I varie de
I0
= 1,0
×10–12
W. m–2 à 102
W. m–2
-

Chap
N° 02 (2010) Caractéristiques
des ondes.
Chap N° 17 Sons et effet Doppler
Sons purs et sons complexes :
-
Son pur :
Un son pur est un son dont le spectre de fréquences est constitué d’une seule
vibration sinusoïdale appelé fondamental.
-
Son complexe : Un son
complexe est formé d’une superposition de vibrations sinusoïdales ayant des
amplitudes et des fréquences différentes.
-
Un diapason émet un son pur,
c’est-à-dire un son dont le spectre en fréquences n’est composé que d’un
fondamental.
-
Le premier son est un son
complexe.
-
Les deux autres sons sont
sinusoïdaux. On parle de sons purs.
-
Le spectre en fréquences d’un
son est la représentation graphique de l’amplitude de ses composantes
sinusoïdales en fonction de la fréquence.
-
Exemple :
-
Le spectre en fréquences d’un
son est la représentation graphique de l’amplitude de ses composantes
sinusoïdales en fonction de la fréquence.
-
Un son complexe est
formé d’une superposition de vibrations sinusoïdales ayant des amplitudes et des
fréquences différentes.
-
En 1822, le
mathématicien français Joseph FOURIER
a montré que :
-
Tout signal périodique de
fréquence f1
peut être décomposé en une somme de signaux sinusoïdaux de fréquences fn
multiples de f1.
-
Avec
fn
= n .
f1
et n
€ N*
-
La fréquence
f1
est appelée le fondamental.
-
C’est la fréquence la plus
basse.
-
Elle fixe la hauteur
du son ou la note de musique
-
Les fréquences 2
f1,
3 f1,
…, n.f1
sont appelées harmoniques.
-
L’analyse spectrale
d’un son permet d’en obtenir le spectre en fréquences.
-
Le spectre en fréquences d’un
son est la représentation graphique de l’amplitude de ses composantes
sinusoïdales en fonction de la fréquence.
Analyse spectrale :
-
Tout signal périodique de
fréquence f1
peut être décomposé en une somme de signaux sinusoïdaux de fréquences
fn
multiples de f1.
-
Avec
fn
= n.f1
et n
€ N*
-
La fréquence
f1 est appelée le
fondamental.
-
Les fréquences 2
f1,
3 f1,
…, n.f1
sont appelées harmoniques.
-
L’analyse spectrale d’un son
permet d’en obtenir le spectre en fréquences.
-
Le spectre en fréquences d’un
son est la représentation graphique de l’amplitude de ses composantes
sinusoïdales en fonction de la fréquence.

-
Dans le cas présent :
-
La fréquence du fondamental :
f1
≈ 350 Hz
-
Les différentes harmoniques :
f2
= 2 f1
≈ 700 Hz ; f3
= 3 f1
≈ 1050 Hz ; f4
= 4 f1
≈ 1400 Hz
Chap N° 20 Numérisation de l’information
Signaux numériques :
-
Convertisseur
analogique-numérique (CAN) :
-
Les systèmes de mesure
analogique sont progressivement remplacés par des systèmes d’acquisition
numérique.
-
Le stockage, la duplication
et le transport des signaux numériques sont plus fiables.
-
Les ordinateurs ne traitent
que des signaux numériques.
-
Les grandeurs analogiques
varient de façon continue au cours du temps.
-
Les grandeurs numériques
varient de façon discrète au cours du temps.
-
Les informations numériques
sont codées en langage binaire (0, 1).

Numérisation d’un signal analogique :
-
Les grandeurs analogiques
varient de façon continue au cours du temps.
-
Les grandeurs numériques
varient de façon discrète (discontinu) au cours du temps.
-
Les informations numériques
sont codées en langage binaire.
-
Il désigne le procédé qui
permet de passer d’un signal analogique à un signal numérique.
-
Les étapes principales de
toute conversion analogique-numérique sont :
-
L’échantillonnage,
-
La
quantification,
-
Et le
codage.
-
L’échantillonnage :
-
Le convertisseur
analogique-numérique prélève des échantillons du signal analogique à intervalles
de temps Te
égaux appelés période d’échantillonnage.
-
La fréquence
d’échantillonnage fe
est le nombre de prélèvements effectués par seconde (nombre de mesures
effectuées par seconde).
-
Elle définit le nombre de
valeurs prélevées au signal analogique par seconde.
-
Elle s’exprime en Hz, MHz, …
-
C’est l’inverse de la période
d’échantillonnage :
-

-
Remarque :
-
La fréquence
d’échantillonnage est réglable.
-
La fréquence
d’échantillonnage doit être supérieure :
-
au
double
de la plus haute fréquence contenue dans le signal d’entrée afin de pouvoir
reconstituer fidèlement le signal (Critère de
Shannon).
-
Ainsi pour échantillonner la
musique, comme l’oreille est sensible aux fréquences sonores comprises entre 20
Hz et 20kHz,
-
On peut prendre une fréquence
échantillonnage de 40 kHz.
-
On perd toutes les fréquences
supérieures à 20 kHz, mais cela n’est pas grave car l’oreille humaine ne les
entend pas.
-
Ainsi, le son
de qualité CD est
échantillonné à 44 kHz.
-
La quantification :
-
L’échantillonnage consiste à
prélever certaines valeurs d’une fonction continue.
-
On se retrouve avec une
succession de nombres réels avec un très grand nombre de décimales.
-
Mais la mémoire des
ordinateurs n’est pas infinie, elle est limitée.
-
Pour limiter le nombre de
valeurs, on va faire une approximation :
-
On ne va retenir que les
valeurs selon un certain pas p
de quantification.
-
La quantification consiste à
affecter une valeur numérique à chaque échantillon prélevé.
-
Chaque valeur est arrondie à
la valeur permise la plus proche par défaut.
-
Le signal est donc quantifié
et ne peut prendre que certaines valeurs discrètes.
-
C’est la
quantification.
-
Cette quantification est liée
aux limites de la perception humaine et des appareils qui transmettent le signal
-
Le codage :
-
La valeur permise est codée
par un nombre binaire.
-
Les valeurs numérisées vont
être stockées sous forme de bits.
-
Un bit est une unité
d’information qui ne peut prendre que deux valeurs : 0 ou 1.
-
Avec 2 bits,
on 22 = 4 ; valeurs
associées : 00 ; 01 ; 10 ; 11
-
Avec 3 bits, 23
= 8 ; valeurs associées : 000 ; 001 ; 010 ; 011 ; 100 ; 101 ; 110 ; 111.
-
Ainsi de suite :
-
Un signal
numérisé sur 8 bits (un octet), peut prendre 28
= 256 valeurs.
-
De 0000 0000 à 1111 1111.
-
Remarque :
-
La qualité de la conversion
analogique-numérique, ou numérisation, est d’autant plus grande :
-
que le pas
p
du convertisseur est petit
-
et que la fréquence
fe
d’échantillonnage est élevée
|
|