Pour aller plus loin : 

I- Propagation d’une perturbation.

1)- Exemples :

a)- Des rondes dans l’eau :

-  On fait tomber un objet dans l’eau et on enregistre le mouvement observé.

-  On observe le déplacement d’une ride circulaire.

Vidéo :

Goutte d'eau

-  Le milieu de propagation de la perturbation est le plan d’eau ; c’est un milieu à deux dimensions.

-  La perturbation se déplace dans toutes les directions à partir du point source S.

-  Un point de la surface de l’eau s’élève lors du passage de la perturbation et reprend sa position initiale.

-  On est en présence d’une onde transversale.

animation :

b)- Compression des spires d’un ressort :

-   un ressort est tendu horizontalement.

-   On comprime quelques spires à une extrémité, puis on lâche brusquement.

-  On observe le déplacement de la compression le long du ressort.

Ressort 

-   Le milieu de propagation est unidimensionnel, la direction de propagation est l’axe du ressort.

-  Une spire du ressort se déplace parallèlement à l’axe du ressort et reprend sa position d’équilibre après le passage de la perturbation.

-  On est en présence d’une onde longitudinale.

c)- Propagation d’une perturbation le long d’une corde : 

-  On soumet une corde horizontale à une brusque secousse verticale.

-  On observe le déplacement de la perturbation le long de la corde.

Corde 

- Le milieu de propagation est unidimensionnel, la direction de propagation est la corde.

-  La perturbation se déplace le long de la corde sans transport de matière.

-  La déformation a lieu perpendiculairement à la direction de propagation.

-  On est en présence d’une onde transversale.

2)- Définitions.

- La corde, le ressort et l’eau constituent des milieux matériels.

-  Dans chaque cas, on crée une perturbation et on observe le déplacement d’une onde mécanique progressive.

- Une perturbation correspond à la variation d’une propriété mécanique des points d’un milieu matériel.

-  C’est pour cela que l’on dit qu’un mobile se déplace alors qu’une onde se propage.

-  La propagation de l’onde mécanique peut se faire dans des milieux à une, deux ou trois dimensions.

-  Après le passage de la perturbation, chaque point du milieu matériel reprend sa position initiale.

-  On dit que le milieu matériel est élastique.

3)- Ondes longitudinales et ondes transversales.

-  C’est le cas de la corde : la direction de propagation de l’onde est celle de la corde (horizontale) et la déformation de la corde a lieu perpendiculairement à la corde.

- C'est le cas du ressort, de la propagation d'un son.

II- Propriétés des ondes mécaniques.

1)- Mécanisme de la propagation.

-  Quels sont les mécanismes nécessaires à la propagation d’une onde mécaniques ?

-  La propagation d’une onde mécanique nécessite un milieu matériel élastique.

-   Une onde mécanique se transmet de proche en proche dans le milieu matériel.

-   Les solides permettent la propagation d’ondes transversales ou d’ondes longitudinales.

-  Dans les fluides, seules les ondes longitudinales peuvent se propager.

2)- Direction de propagation.

-  Une onde se propage à partir de la source S dans toutes les directions qui lui sont offertes par le milieu matériel.

-  Dans le cas de la corde, l’onde ne peut se propager que dans une direction, celle de la corde.

-  Dans le cas de d’un milieu à deux dimensions comme une étendue d’eau, l’onde se propage dans toutes les directions possibles du plan d’eau.

-  Un son se propage dans l’air dans toutes les directions qui les sont offertes.

-  Il se déplace dans un milieu à 3 dimensions, dans l’espace.

3)- Transport d’énergie.

-  Une onde réalise un transfert d’énergie mécanique sans transport de matière.

-  Pour produire la perturbation, il faut fournir de l’énergie.

-  La perturbation se propage.

-  Chaque point du milieu matériel revient à sa position initiale après le passage de la perturbation.

-  De l’énergie mécanique a été transférée du point S, la source au point M du milieu matériel.

-  Il n’y a pas de transport de matière.

- Si l’on néglige les pertes lors de la propagation, on dit que l’énergie se conserve.

- Dans le cas d’un milieu à une dimension, chaque point du milieu récupère intégralement l’énergie de la source au passage de la perturbation.

- Dans le cas d’un milieu à deux dimensions, l’énergie se répartie sur la surface.

-  L’énergie qui arrive en un point donné est d’autant plus faible que l’on s’éloigne de la source.

-  Cas d’un milieu à trois dimensions : idem.

4)- Superposition de deux ondes.

-   Deux ondes mécaniques peuvent se superposer sans se perturber.

-  Lorsque les deux perturbations se croisent, leurs amplitudes s’ajoutent algébriquement.

-  Après le croisement, chaque perturbation reprend sa forme propre.

Vidéo

Vidéo

Vidéo

III- célérité d’une onde.

1)- Définition.

-   La vitesse à laquelle la perturbation se propage s’appelle la célérité de l’onde.

-  Cette vitesse est évaluée dans le référentiel lié au milieu.

-  On appelle célérité la vitesse de propagation de l’onde, pour la distinguer de la vitesse de déplacement d’un corps.

-  La célérité d’une onde mécanique dépend du milieu de propagation.

-   C’est une caractéristique du milieu de propagation.

-  Elle ne dépend pas de l’amplitude de la déformation.

-   La célérité est le quotient de la distance parcourue sur la durée de parcours.

- 

2)- Influence du milieu.

a)- Influence de l’inertie du milieu.

-  Que représente l’inertie d’un milieu ?

-  Exemples : pour un solide en translation, l’inertie du solide est représentée par sa masse. 

-  Plus la masse d’un solide est grande, plus il est difficile de le mettre en mouvement et plus son inertie est grande.

-  L’inertie d’une corde est représentée par sa masse par unité de longueur, sa masse linéique.

-  Pour un solide en rotation, c’est la répartition de la masse par rapport à l’axe de rotation qui intervient.

-  Plus la masse du solide est éloignée de l’axe, plus il est difficile de le mettre en mouvement et plus son inertie est grande.

- La célérité d’une onde dans un milieu dépend de son inertie.

-  Plus l’inertie du milieu est grande et plus la célérité de l’onde se propageant dans ce milieu est faible.

b)- Influence de la rigidité d’un milieu.

- Que représente la rigidité d’un milieu ?

- La rigidité d’un milieu représente la résistance que ce milieu oppose lorsqu’on cherche à le déformer.

- Exemples : Dans le cas d’un ressort, la rigidité du ressort est caractérisée par sa constante de raideur k.

-  La rigidité d’une corde est mesurée par sa tension T, qui est la force exercée sur la corde pour la tendre.

-  La célérité d’une onde dépend de la rigidité du milieu dans lequel elle se propage. Plus le milieu est rigide et plus grande est sa célérité.

IV- Les Ondes sonores. (Utiliser le logiciel soncandi)

1)- La nature de la perturbation.

- Propagation d’un son dans l’air.

-  Montage : G.B.F et H.P.

-  On émet un son dans l’air.

-  L’air est un mélange de gaz.

-  Il se comporte comme un gaz.

-  Il est compressible et expansible, élastique….

- Lors de l’émission d’un son, la membrane du H.P se déplace.

-  En avançant, elle crée une compression, elle comprime les couches d’air voisines de sa surface.

-  L’air comprimé pousse dans toutes les directions l’air qui l’entoure et reprend sa position initiale.

-  La compression se propage de proche en proche, c’est l’onde sonore.

-  La perturbation crée par la membrane est une variation de pression.

-  Si p₀ est la pression initiale, et p la pression lors de la compression, la variation de pression est δp = p – p₀.

-  L’oreille détecte le son émis par le H.P car elle est sensible à la variation de pression δp bien qu’elle soit faible par rapport à la pression atmosphérique.

2)- Les propriétés du son.

-  Le son est une onde longitudinale la direction de propagation est parallèle à la direction de la perturbation.

-  La propagation d’un son nécessite un milieu matériel.

-  Le son ne se propage pas dans le vide.

-  Le son transporte de l’énergie.

3)- Célérité du son.

- La célérité du son dépend du milieu de propagation.

-  La célérité du son est plus grande dans les solides que dans les liquides et le gaz.

-  Car moins le milieu est compressible, plus il est difficile à déformer et plus il est rigide.

-  Plus il est rigide, plus grande est sa célérité.

V- Onde progressive à une dimension.

1)- Définition.

-  Une onde mécanique progressive à une dimension est une onde qui se propage dans une seule direction.

- Une onde progressive à une dimension a pour direction de propagation une droite.

-  Elle peut se propager dans un milieu à une, deux ou trois dimensions.

2)- Mouvement de la source.

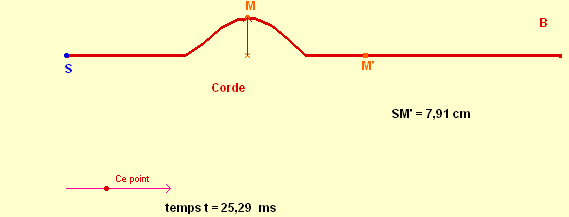
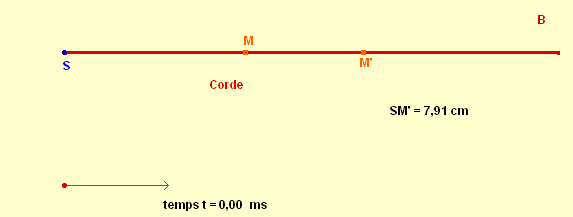
- On considère la propagation d’une perturbation le long d’une corde horizontale.

- Dans un premier temps, on crée la perturbation au point S de la corde.

-  La source S monte pendant la durée Δt₁ puis redescend pendant la durée Δt₂.

-  Le mouvement de S est un mouvement rectiligne vertical.

- On repère la direction de propagation de l’onde à l’aide de l’axe (x’x) et on repère la position de la source S grâce à l’axe (y’y).

Exemple :

Vidéo :

- On note y_S (t), la fonction mathématique représentant les positions de la source au cours du temps.

3)- Mouvement d’un point M du milieu matériel.

-  La perturbation crée au point S de la corde au temps t₀ se propage de proche en proche.

-  Elle atteint le point M, puis le point M’ du milieu matériel.

-  Chaque point du milieu matériel reproduit la perturbation de la source S (on suppose que la perturbation se propage sans amortissement).

- La perturbation au point M reproduit la perturbation de la source S avec un retard τ, car la perturbation met un certain temps pour progresser de S à M.

- Le retard t est la durée mise par l’onde pour se propager de S à M :

- En conséquence, si v est la célérité de l’onde et SM la distance parcourue par l’onde :

- Si on repère chaque point de la corde par son abscisse x,

-  La source S est située à l’origine des abscisses :

- L’abscisse du point M est notée : x_M.

-  Le mouvement d’un point M situé à la distance x_M de la source est le même que celui de la source avec un retard  :

- 

-  La courbe représentant le mouvement de M en fonction du temps est la même que celle de la source décalée de la durée τ.

-  Si y_S (t), représente la position de la source au cours du temps, le mouvement de M est y_M (t),

- Avec : y_M (t) = y_S (t - τ)  car l’onde se propage de S vers M.

- Dans une onde mécanique, tout point du milieu subit la même perturbation avec un retard

- La perturbation au point M’ à l’instant t’ est celle qui se trouvait en M à l’instant antérieur t = t’ – τ.

- Avec   , durée qui représente le retard de l’onde entre les points M et M’.

4)- Exemple 1 :

-  On crée une onde mécanique progressive sur une corde en produisant, à son extrémité S, une perturbation très brève à l’instant t = 0 s.

-  L’onde se propage sur la corde avec la célérité v = 5,0 m / s.

a)- Le point M situé à 10 m de la source S est-il en mouvement à la date t = 2,5 s ? Justifier la réponse.

- Chaque point de la corde reproduit la perturbation créée en S avec un retard τ.

- L’onde se propage du point S (la source) vers le point M. Pour le point M situé à la distance SM = 10 m, le retard est donné par l’expression suivante :

  -   

- Le point M effectue un mouvement à la date t = t₀ + τ, en conséquence à la date t = 2,0 s.

-  Comme la durée de la perturbation est brève, on peut considérer que le point M n’est plus en mouvement à la date t = 2,5 s.

b)- Même question pour le point N placé à 15 m de la source S.

-  L’onde se propage du point S (la source) vers le point N. Pour le point N situé à la distance SN = 15 m, le retard est donné par l’expression suivante :

- 

-  Le point N effectue un mouvement à la date t = t₀ + τ : t = 3,0 s.

-  En conséquence, à la date t = 2,5 s, la perturbation n’a pas atteint le point N.

-  Il n’est pas en mouvement.

5)- Exemple 2 : Mesure d’un retard à l’oscilloscope. Voir exercice 19 page 42.

VI- Applications.

1)- QCM :

2)- Exercices :