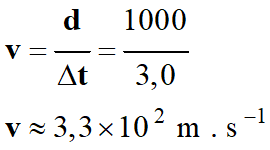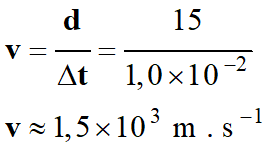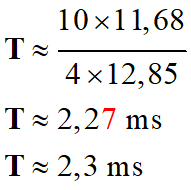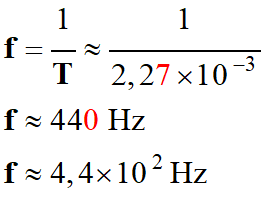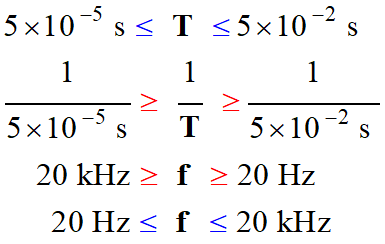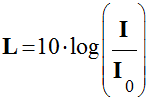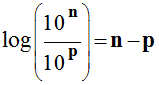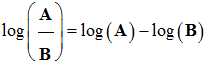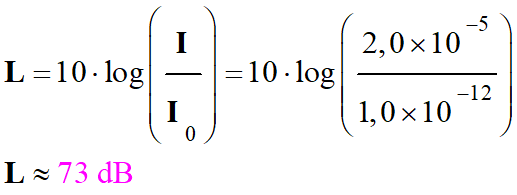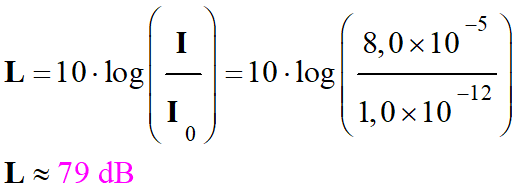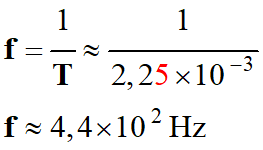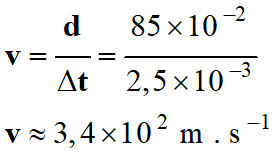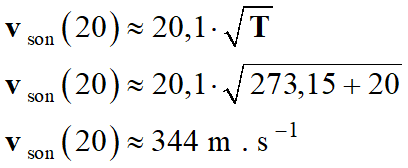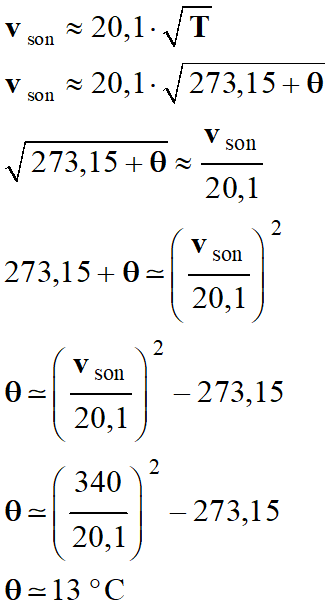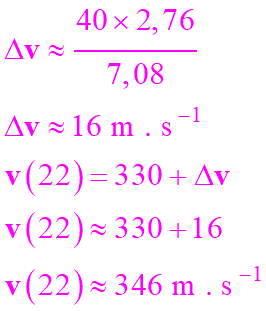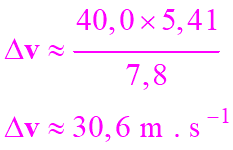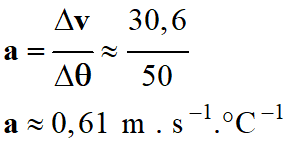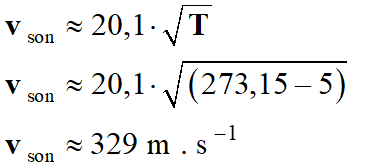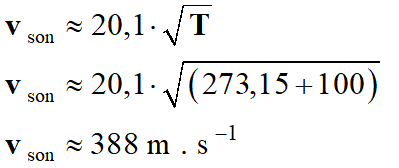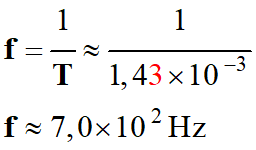Émission et propagation d’un son.
Exercices.
|
|
1)- Exercice 5 page 216 : Comparer des valeurs de vitesse :
|
Comparer des valeurs de vitesse : Un signal sonore pet 3,0 s pour parcourir 1000 m dans l’air. Il parcourt 15 m dans l’eau liquide en 1,0 × 10–2 s. 1.
Calculer les valeurs des vitesse de
propagation d’un signal sonore dans l’air et dans l’eau
liquide. 2.
En comparant ces valeurs, en déduire une
propriété concernant l’influence de l’état physique
du milieu sur la vitesse de propagation d’un signal sonore. |
|
Comparer des valeurs de vitesse : 1.
Valeurs des vitesse de propagation d’un
signal sonore
-
Valeurs des vitesse de propagation
d’un signal sonore dans l’air :
-
Distance parcourue
d = 1000 m
-
Durée de parcours :
Δt = 3,0 s
-
Relation :
-
-
AN :
-
Valeurs des vitesse de propagation
d’un signal sonore dans l’eau liquide :
-
Distance parcourue
d = 15 m
-
Durée de parcours :
Δt = 1,0 × 10–2 s
-
AN :
-
2.
Influence de l’état physique du milieu sur
la vitesse de propagation d’un signal sonore.
-
Un signal sonore se dépasse plus vite
dans un état condensé (solide ou liquide) que dans un état dispersé
(gazeux). |
2)- Exercice 6 page 216 : Déterminer la période d’un signal sonore :
|
Déterminer la période d’un signal sonore :
-
Déterminer la valeur la période
T su signal sonore émis
par un diapason dont l’enregistrement est donné ci-dessus.
-
En déduire la valeur de la fréquence
f du signal sonore. |
|
Déterminer la période d’un signal sonore :
-
Valeur la période
T su signal sonore émis
par un diapason dont l’enregistrement est donné ci-dessus.
-
Mesures effectuées avec Word sur le
graphique :
-
4 T ↔ 11,68 cm
et 10 ms ↔ 12,85 cm
-
On en déduit la valeur de la période
du signal sonore :
-
-
Valeur de la fréquence
f du signal sonore.
-
-
Le diapason donne le
la 3 (janvier 1975). |
3)- Exercice 8 page 217 : Calculer un domaine de fréquence :
|
Calculer un domaine de fréquence : Les sons audibles ont une période T comprises entre 5 ×10–5 s et 5 ×10–2 s. 1.
Rappeler le domaine des fréquences des sons
audibles par l’être humain. 2.
Retrouver ce domaine à partir des périodes
indiquées en introduction. |
|
Calculer un domaine de fréquence : 1.
Rappel du domaine des fréquences des sons
audibles par l’être humain.
-
L’oreille humaine est un récepteur
sensible aux ondes sonores dont la fréquence est comprise entre 20 Hz et 20 kHz.
-
Domaines des ondes sonores : 2.
Retrouver ce domaine à partir des périodes
indiquées en introduction.
-
Les sons audibles ont une période
T comprises entre 5 ×10–5 s et 5 ×10–2 s.
-
On peut écrire :
-
|
4)- Exercice 9 page 217 : Représenter un domaine de fréquences :
|
Représenter un domaine de fréquences : Le tableau ci-dessous indique les domaines des fréquences des sons audibles par quelques animaux
1.
Sur un
axe gradué en hertz, placer sans souci d’échelle, les domaines des sons audibles
par l’être humain, les ultrasons et les infrasons. 2.
Y ajouter les domaines de fréquences des
sons audibles par les animaux cités dans le
tableau. |
|
Représenter un domaine de fréquences :
1.
Les
domaines des sons audibles par l’être humain, les ultrasons et les infrasons.
-
Diagramme : 2.
Domaines de fréquences des sons audibles par
les animaux cités dans le tableau.
-
Diagramme : |
5)- Exercice 13 page 217 : Relier des grandeurs :
|
Relier des grandeurs ; Lorsque l’intensité sonore I double, le niveau d’intensité
sonore L augmente de 3 décibels.
-
Compléter le tableau ci-dessous à
l’aide de l’information précédente.
|
|
Relier des grandeurs ; Lorsque l’intensité sonore I double, le niveau d’intensité
sonore L augmente de 3 décibels.
-
Tableau :
-
Additif ;
-
L’intensité sonore, notée I, caractérise l’intensité du
signal
reçue par l’oreille.
-
Elle
s’exprime en watt par mètre carré : W / m2 ou W. m–2
-
L’oreille humaine normale perçoit les
signaux sonores dont l’intensité est comprise entre
-
Une valeur
minimale I0 = 1,0
× 10–12
W. m–2 (seuil d’audibilité)
-
Et une
valeur maximale Imax = 25 W. m–2 (seuil
de douleur). - Comme l’écart entre ces deux valeurs est très grand, on a créé unenouvelle grandeur, qui utilise une échelle logarithmique, appelée le
niveau d’intensité sonore, notée
L.
-
Relation mathématique :
-
La notation log fait référence
à la fonction logarithme décimal.
-
Ainsi, l’échelle de niveau
d’intensité sonore L varie de 0 dB à environ 140 dB.
-
Alors que l’intensité sonore I
varie de I0 = 1,0
x 10–12 W. m–2 à 102 W. m–2
-
Quelques propriétés de la fonction
logarithme décimal :
-
-
-
Cours : Caractéristiques des ondes - Pour vérifier, on peut utiliser la formule suivante : -
-
Colonne 1 :
-
-
Colonne 4 :
-
-
Colonne 5 :
-
|
6)- Exercice 14 page 217 : Évaluer une exposition sonore :
|
Évaluer une exposition sonore :
-
Quelle information complémentaire manque-t-il à cette affiche pour que
l’utilisateur soit protégé des risques sonores ?
|
|
Évaluer une exposition sonore :
-
Information complémentaire :
-
Il manque la notion de durée :
-
L’exposition sonore tient compte du
niveau d’intensité sonore L et de la durée d’exposition auxquels l’oreille est soumise.
-
Plus le niveau d’intensité sonore et
la durée d’exposition sont élevés et plus les risques d’atteinte de l’audition sont
importants.
-
La puissance sonore maximale de
sortie d'un baladeur musical ne peut excéder 100 dB (A) et l’utilisateur doit être informé
lorsque le niveau sonore dépasse 85 dB (A) - Le décibel dB (A), ou décibels avec la pondération «A», simule la perception par l’oreille de l’intensité sonore en tenant compte de la sensibilité moyenne des personnes. |
7)- Exercice 17 page 218 : L’oreille humaine :
|
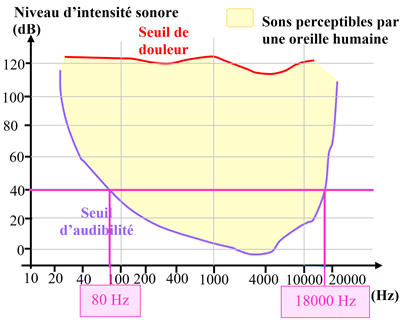
L’oreille humaine : Le graphique ci-dessous représente, dans la zone jaune, les niveaux d’intensité sonore des sons audibles en fonction de la fréquence du son perçu par l’oreille humaine. 1.
Estimer la fréquence pour laquelle la sensibilité de
l’oreille humaine est la plus grande. 2.
Dans quel domaine de fréquences l’oreille humaine entend-elle
des sons dont le niveau d’intensité sonore est de 40 dB ? 3.
À partir de quel niveau d’intensité sonore l’oreille humaine
peut-elle entendre un son de 40 Hz ? 4.
L’oreille humaine entend des sons dont les fréquences sont
comprises entre 20 Hz et 20 kHz. Cette information est-elle complète ? 5.
Indiquer si la hauteur des sons est un facteur de risque ? 6.
Localiser sur le diagramme le domaine des ultrasons. |
|
L’oreille humaine : 1.
Fréquence pour laquelle la sensibilité de
l’oreille humaine est la plus grande.
-
La sensibilité de l’oreille humaine
est la plus grande pour un signal sonore de 4000 Hz environ.
-
Pour cette fréquence, le seuil
d’audibilité est le plus bas. 2.
Domaine de fréquences des sons dont le
niveau d’intensité sonore est de 40 dB pour l’oreille
humaine :
- Pour un niveau d’intensité sonore L = 40 dB, le domaine de fréquences audible est compris entre 80 Hz et 18000 Hz environ (l’échelle n’est pas
linéaire). 3.
Niveau d’intensité sonore de l’oreille
humaine pour entendre un son de 40 Hz :
-
Un son de fréquence
f = 40 Hz est perceptible si le niveau d’intensité sonore L ≥ 58 dB. 4. L’oreille humaine entend des sons dont les fréquences sont comprises entre 20 Hz et 20 kHz. Cette information est-elle
complète ?
-
Pour que l’information soit complète,
il faut préciser le niveau d’intensité sonore
L. - Pour être audible, les sons compris entre 20 Hz et 20 kHz doivent être à des niveaux sonores L élevés. Supérieur à 70 dB pour les sons proches de 20 kHz et supérieur à 110 dB pour les sons proches de 20 Hz. 5.
La hauteur des sons :
un facteur de risque :
-
Le seuil de la douleur est
pratiquement constant sur le domaine 20 Hz à 20 kHz.
-
La fréquence d’un son ou sa hauteur
n’est pas beaucoup d’influence sur la dangerosité.
-
La hauteur d’un son n’est pas un
facteur à risque. 6.
Localiser sur le diagramme le domaine des
ultrasons. |
|
Accorder une guitare avec un diapason : Avant de jouer un morceau de musique à la guitare, il est nécessaire de l’accorder. Pour cela, on peut utiliser un diapason qui émet un La3 dont la
fréquence est parfaitement connue. On réalise les enregistrements de signaux sonores émis par une diapason et une guitare. A.
Enregistrement sonore du diapason. B.
Enregistrement sonore de la guitare. 1.
Déterminer la période de chacun des sons. 2.
Calculer leur fréquence. 3.
La guitare est accordée si les deux
fréquences sont égales. Est-ce le cas ? 4. Le microphone est placé à la même distance des deux sources sonores. Lequel des deux
sons a le niveau d’intensité sonore le plus grand ? |
|
Accorder une guitare avec un diapason :
1.
Période de chacun des sons.
-
Période su signal émis par le
diapason :
-
Lecture graphique :
-
4
T ≈ 9,0 ms
-
T ≈ 2,25
ms
-
T ≈ 2,3 ms
-
Période du signal émis par la
guitare :
-
Lecture graphique :
-
4
T ≈ 9,0 ms
-
T ≈ 2,25
ms
-
T ≈ 2,3 ms 2.
Valeur de la fréquence.
-
Comme la période
T est la même, les deux signaux sonores ont la même fréquence.
-
-
Pour ce résultat, on garde la valeur
intermédiaire de la période dans la calculatrice. - Remarque : si on prend la valeur T = 2,3 ms, - Alors
f ≈ 4,3 × 102 Hz - Remarque : la fréquence du La3 est 440 Hz (A 440). Cette norme a été acceptée par l’Organisation internationale de normalisation
(ISO) en 1955 en tant que ISO 16. 3.
La guitare est accordée car les deux
fréquences sont égales (la corde La).
-
Le diapason permet d’accorder la
cinquième corde de la guitare (la corde
La).
-
Ensuite on accorde les autres cordes. - On peut accorder les autres cordes en appuyant sur la cinquième case et en comparant la note avec celle produite par la corde suivante (ceci est valable pour les cordes, 1, 3, 4, 5, 6)
-
Pour la corde 2, il faut appuyer sur
la quatrième case de la corde 3 et comparer les notes produites par les cordes 2 et 3.
-
Accordage : Mi, La, Ré, Sol, Si, Mi
(chanterelle)
4.
Le niveau d’intensité sonore :
-
Le signal sonore émis par la guitare a un niveau
d’intensité sonore plus élevé que le signal sonore émis par le
diapason.
-
La tension du signal électrique
obtenu est plus grande pour celui de la guitare.
-
L’amplitude du signal sonore reçu de la guitare est
plus grande que l’amplitude du signal sonore reçu
du diapason.
-
Pour amplifier le son émis par le
diapason, on peut l’exciter et le poser sur la caisse de résonance de la guitare.
|
9)- Exercice 24 page 220 : Détermination de la vitesse de propagation des ultrasons :
|
Détermination de la vitesse de propagation des ultrasons : On se propose de déterminer la valeur de la vitesse de propagation des ultrasons dans l’air. Un émetteur et un récepteur de salves ultrasonores sont placés face à face, à une distance d = 85 cm st sont
connectés à un oscilloscope numérique. On obtient les courbes représentées ci-dessous. 1.
Expérience : a.
Schématiser le montage expérimental. b.
Que se passe-t-il aux instants repérés par
les points A et B sur les courbes ? c.
Calculer la valeur de la vitesse v de
propagation des ultrasons dans les conditions de
l’expérience. 2.
Vitesse de propagation d’un signal sonore : a.
Rappeler la valeur approchée de la vitesse
de propagation du son dans l’air. b.
Comparer les valeurs de la vitesse de
propagation du son et des ultrasons dans l’air. |
|
Détermination de la vitesse de propagation des ultrasons :
1.
Expérience : a.
Schéma du montage expérimental. Ou b.
Les instants repérés par les points A
et B sur les courbes : - Point A : émission du signal ultrasonores (position de l’émetteur ultrasonores) - Point B : réception du signal ultrasonores (position du récepteur ultrasonores) c.
Valeur de la vitesse v de propagation
des ultrasons dans les conditions de l’expérience.
-
Distance parcourue par les
ultrasons :
-
d = 85 cm
-
Durée du parcours :
-
Δt = 2,5 ms
-
Relation :
-
-
AN :
-
2.
Vitesse de propagation d’un signal sonore : a.
Rappeler la valeur approchée de la vitesse
de propagation du son dans l’air.
-
La valeur approchée de la vitesse de
propagation d’un signal
sonore dans l’air à environ 20 ° C est :
-
v
≈
340 m / s.
-
cette vitesse dépend de la
température.
-
La célérité du son dépend du milieu
de propagation. b.
Comparer les valeurs de la vitesse de
propagation du son et des ultrasons dans l’air.
-
Les ondes ultrasonores se déplacent à
la même vitesse que
les sons.
-
L’air n’est pas un milieu dispersif
pour les ondes sonores.
-
Additif :
-
On admet que la célérité du son dans
l’air est proportionnelle
à la racine carrée de la température
absolue T.
-
-
Avec
T (K) ≈
θ ° C + 273 - On peut calculer la vitesse de propagation d’un signal sonore
à 0 ° C :
-
-
Vitesse de de propagation d’un signal
sonore à 20 ° C :
-
-
On peut retrouver la température de
la classe le jour de
l’expérimentation :
-
- Il fait un peu froid dans la classe. |
10)- Exercice 26 page 221: Propagation du son et température de l’air :
|
Propagation du son et température de l’air : On a représenté, sur le graphique ci-dessous, l’évolution de la vitesse de propagation d’un signal sonore dans l’air en fonction de la température θ. 1.
Comment évolue la valeur de la vitesse de
propagation d’un signal sonore dans l’air en
fonction de ce paramètre ? 2.
Par lecture graphique, déterminer la valeur
de la vitesse du son dans l’air à 22 ° C. 3.
Modélisation : a. Modéliser l’évolution de la valeur de la vitesse du son dans l’air en fonction de la température par l’équation d’une droite du type : v = a .
θ + b, en précisant a et b. b. Estimer alors la valeur de la vitesse du son dans l’air à – 5 ° C puis à 100 ° C. |
|
Propagation du son et température de l’air : 1.
Évolution la valeur de la vitesse de
propagation d’un signal sonore dans l’air en
fonction de la température.
-
La courbe v =
f (θ) est une fonction croissante
de la température.
-
La vitesse de propagation d’un signal
sonore dans l’air augmente avec la température de l’air. 2.
Valeur de la vitesse du son dans l’air à 22
° C.
-
3.
Modélisation : a.
Équation de
la droite du type : v = a . θ + b,
en précisant a et b. - On est en présence d’une fonction affine du type : - v = a .
θ +
b
-
L’ordonnée à l’origine :
b ≈ 332 m . s–1
-
Le coefficient directeur de la
droite :
-
-
Exploitation graphique :
-
-
Valeur du coefficient directeur de la
droite :
-
-
v (m . s–1) =
332 + 0,61 θ (° C) b.
Estimation la valeur de la vitesse du son
dans l’air
-
Dans le cas présent, on fait une
extrapolation :
-
Valeur de la vitesse du son dans
l’air à – 5 ° C
-
v = 332 + 0,61
θ
-
v = 332 + 0,61
× (– 5)
-
v ≈ 329 m . s–1
-
Valeur de la vitesse du son dans
l’air à 100 ° C.
-
v = 332 + 0,61
θ
-
v = 332 + 0,61
× (100)
-
v ≈ 393 m . s–1
-
On peut utiliser la formule suivante
pour vérifier :
-
-
Valeur de la vitesse du son dans
l’air à
θ = – 5 ° C
-
-
Valeur de la vitesse du son dans
l’air à
θ = 100 ° C
-
- À comparer avec la valeur trouvée précédemment : v ≈ 393 m . s–1 - Dans ce cas, l’extrapolation est importante (le domaine d’étude est compris entre 0 ° C et 50 ° C)
-
Alors que pour
θ = – 5 ° C, l’extrapolation est proche du domaine d’étude. |
11)- Exercice 29 page 222 : DS : Test d’audiométrie tonale :
|
DS : Test d’audiométrie
tonale : durée 30 min L’audiométrie tonale est un test réalisé en cabine insonorisée. Le principe de ce test est de diffuser des sons d’intensité sonore croissante et de fréquences variables (de 1,25 × 102 Hz à 8,00 × 103 Hz). Le patient doit appuyer sur un bouton dès qu’il perçoit le son. Le son atteint l’oreille interne par voie aérienne (via le tympan
et les osselets) et par voie osseuse. L’audiométrie tonale teste les deux voies.
A.
Représentation du signal sonore
diffusé.
B.
Audiogramme :
-
Les résultats des tests d’audiogramme
sont fournis sous forme d’une courbe appelée audiogramme.
-
Les fréquences, en hertz, sont en
abscisse et la perte auditive exprimée en dB (dB) en ordonnée.
C.
Audiogramme d’un patient.
-
La courbe ci-dessous révèle le niveau
d’audition d’un patient (courbe violette) par rapport à des valeurs de références dites
normales (courbe verte).
-
Données :
-
Les fréquences de la parole se
situent entre 500 Hz et 2000 Hz.
-
Un signal sonore se propage à environ
3500 m , s–1 dans les os. 1.
Déterminer la fréquence du signal sonore
proposé dans le document A.. 2.
Citer le domaine des fréquences des sons
audibles par l’oreille humaine. 3.
Exploitation de l’audiogramme : a.
Lire la fréquence pour laquelle le patient a
la perte d’audition la plus importante. b.
Cette perte d’audition est-elle gênante lors
d’une discussion. 4.
Comparer les valeurs des vitesses de
propagation du son pour chacune des voies testées lors
de l’audiométrie tonale. |
|
DS Test d’audiométrie tonale : 1.
Fréquence du signal sonore proposé dans le
document A..
-
Pour 14 périodes, on trouve une durée
de 20 ms sur le graphique.
-
Lecture graphique :
-
14
T ≈ 20 ms
-
T ≈ 1,43
ms
-
T ≈ 1,4 ms
-
Valeur de la fréquence (En gardant le
résultat intermédiaire dans la calculatrice)
-
2.
Domaine des fréquences des sons audibles par
l’oreille humaine.
-
L’oreille humaine est un récepteur
sensible aux ondes sonores dont la fréquence est comprise entre 20 Hz et 20 kHz.
-
Domaines des ondes sonores : 3.
Exploitation de l’audiogramme : a.
Fréquence pour laquelle le patient a la
perte d’audition la plus importante.
-
Le patient a un déficit auditif de 40
dB pour la fréquence f =
4000 Hz.
-
C’est un déficit important. b.
Perte d’audition et discussion.
-
Cette perte n'est pas importante pour la
discussion.
-
Cette fréquence ne fait pas partie du
domaine des fréquences de la parole.
-
Les fréquences de la parole se
situent entre 500 Hz et 2000 Hz. 4.
Comparaison des valeurs des vitesses de
propagation du son pour chacune des voies testées lors
de l’audiométrie tonale.
-
La vitesse du son dans l’air est
d’environ 340 m . s–1.
-
Un signal sonore se propage à environ
3500 m , s–1 dans les os.
-
Un signal sonore se déplace dix fois
plus vite dans les os que dans l’air. |
|
|