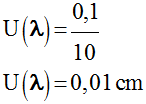|
Chap. N° 02 |
Caractéristiques des ondes. Exercices. |
|
|
|

I- Exercice 6 page 50. Connaître les ondes progressives.
|
1)-
Qu’est-ce qu’une onde progressive ? 2)-
Que transporte une onde ? 3)- Une onde se propage d’un point A à un point B. Comment appelle-t-on la durée que l’onde
met pour se propager de A à B ? |
|
1)-
Onde progressive :
-
Une onde progressive
correspond au déplacement d’une perturbation dans un
milieu. 2)-
Une onde transporte de l’énergie sans déplacement de
matière. 3)-
Durée que l’onde met pour se propager de A à
B :
-
Chaque point du
milieu reproduit la perturbation de la source S. - La perturbation au point B reproduit la perturbation au point A avec un retard τ, - car la perturbation met un certain temps pour progresser de A à B.
- L’onde se propage avec la célérité v.
-
Cette durée est
appelée retard, notée τ. |
II- Exercice 7 page 50. Déterminer une vitesse de propagation.
|
On réalise l’enregistrement de l’élongation, notée y, du point A d’une corde lors de la propagation d’une perturbation Le point
A est situé à 1,50 m de la source
S de la perturbation. On déclenche le chronomètre au début de la perturbation provoquée en S.
1)-
À quelle date tA la perturbation
atteint-elle le point A ? 2)-
Pendant quelle durée
Δt le point A est-il en
mouvement ? 3)-
Quelle est la célérité v de la perturbation ? |
|
1)-
Date tA à laquelle la perturbation
atteint le point A :
-
La courbe représente
les variations de l’élongation de la perturbation en
fonction du temps.
- L’onde arrive au point A, à l’instant tA ≈ 0,20 s, l’élongation est maximale au temps tB ≈ 0,30 s puis l’élongation s’annule au temps tC ≈ 0,25 s.
- Le point A reprend sa position
initiale.
-
En conséquence : le
début de la perturbation atteint le point A à
la date :
-
tA
≈ 0,20 s (lecture graphique). 2)-
Durée
Δt du mouvement du point A :
-
Par lecture
graphique : Δt ≈ 0,050 s 3)- Célérité v de la perturbation : - l’onde parcourt la distance d = 1,50 m pendant la durée : - Δt = tA – t0
= tA ≈ 0,20 s
-
|
III- Exercice 11 page 51. Exploiter une expérience.
|
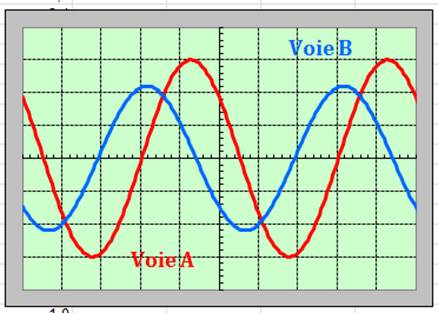
Un haut-parleur, relié à un générateur basses fréquences, émet un signal sonore. Ce signal est capté par deux microphones identiques M1 et M2 situés le long de l’axe du haut-parleur. Ces deux microphones sont reliés à un oscilloscope dont les deux voies ont la même sensibilité verticale et horizontale. On obtient l’oscillogramme suivant :
1)-
Schématiser l’expérience réalisée. 2)-
Quelles sont les différences et les similitudes
entre les deux signaux ? 3)-
Les deux microphones sont-ils à la même distance de
l’émetteur ? Justifier. |
|
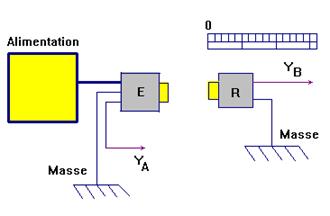
1)-
Schéma de l’expérience :
2)-
Différence(s) et les similitude(s) entre les deux
signaux :
-
Différence(s) :
-
Les deux signaux non
pas la même amplitude.
-
Similitudes :
-
Les deux signaux ont
la même période et de ce fait, la même fréquence.
-
Les deux signaux sont
en phase. 3)-
Position des micros : - Les microphones ne sont pas à la même distance du haut-parleur, car les signaux n’ont pas la même amplitude.
- Le micro M2
est plus éloigné que le micro M1
car l’amplitude du signal reçu est plus petite.
-
Remarque : comme des
deux signaux sont en phase, la distance qui sépare
les deux micros est un multiple de la longueur
d’onde du signal. |
IV- Exercice 12 page 51. Connaître la double périodicité.
|
1)-
Relation : a)-
Rappeler la relation liant
la période spatiale et la période temporelle d’une
onde. b)-
À l’aide des unités de
chacune des grandeurs physiques, vérifier la
cohérence de cette relation. 2)-
Recopier et compléter le tableau suivant :
|
|
1)-
Relation : a)-
Relation liant la période
spatiale et la période temporelle d’une onde :
-
Relation
fondamentale :
b)-
Cohérence de cette
relation :
-
2
)-
Tableau complété : attention aux unités.
|
V- Exercice 16 page 52. Exploiter des spectres sonores.
|
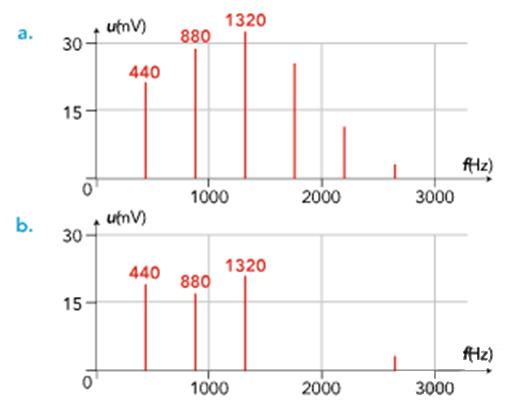
On a réalisé les spectres de
deux notes de musique jouées par deux instruments
1)-
Les notes ont-elles la même hauteur ? Justifier. 2)-
Les timbres sont-ils identiques ? Justifier. |
|
1)-
Hauteur d’un son
-
La hauteur du son est
liée à la fréquence f1 du
fondamental.
-
Le fondamental est la
plus petite fréquence qui apparaît dans le spectre. - Dans chaque cas, la fréquence du fondamental est f1 = 440 Hz.
- C’est la fréquence du La3. 2)-
Timbre d’un son :
-
Le timbre d’un son
dépend du nombre et de l’amplitude des harmoniques
qui sont présents. - Deux sons de même hauteur émis par des instruments différents ne sont pas perçus de la même manière,
car les harmoniques,
associées au fondamental, sont différentes.
-
Les deux sons ont des
timbres différents car les harmoniques associées au
son fondamental sont différentes. |
VI- Exercice 19 page 52. Incertitude sur la mesure.
|
Un groupe d’élèves effectue la
mesure de la célérité des ultrasons dans l’air dans
une pièce à 20 °C. Leurs résultats sont regroupés
dans le tableau ci-dessous :
1)-
Proposer un montage et un protocole permettant de
mesurer la célérité des ultrasons dans l’air avec
une bonne précision. 2)- À partir des mesures obtenues, évaluer la célérité des ultrasons dans l’air à 20 ° C en calculant l’incertitude de répétabilité avec un niveau de
confiance de 95 % (voir fiche N° 3 page 584).
-
Le facteur
d’élargissement k dépend du nombre n de
mesures effectuées et du niveau de confiance
choisi :
-
Tableau pour le
niveau de confiance à 95 % :
3)-
De quel(s) paramètre(s) dépend cette valeur ? |
|
1)-
Montage et protocole expérimental :
-
Montage :
- Réaliser les réglages afin d’obtenir un oscillogramme exploitable (il faut régler la durée de balayage
pour observer une à deux périodes et la sensibilité
verticale pour utiliser les 2/3 de l’écran). - Placer l’émetteur E et le récepteur R de façon à ce que les courbes observées à l’oscilloscope soient en phase (R doit être suffisamment proche de E). - Repérer la position initiale de R. - déplacer R jusqu’à ce que les courbes se trouvent en phase pour la dixième fois.
- On note d le
déplacement correspondant du récepteur R.
-
d =10
λ. - Grâce à l’oscillogramme, on arrive à déterminer la valeur de la fréquence f de l’onde ultrasonore.
- Au
lycée : f ≈ 40 kHz)
-
Exemple :
-
Durée de balayage ou
sensibilité horizontale : b = 5,00
μs / div
-
Déplacement
horizontal pour une période : x
≈
5,0 div
-
T = b .
x
-
T
≈
5,0
× 5,0
-
T
≈
25 μs - La mesure de la longueur d’onde et celle de la période et ainsi de la fréquence
permettent de calculer la célérité des
ultrasons. 2)-
Incertitude de répétabilité :
-
Valeur
moyenne de la célérité :
-
La moyenne
arithmétique est le quotient de la somme des valeurs
vi par le nombre n.
-
On écrit :
-
Pour
calculer la valeur moyenne, on peut utiliser un
tableur (Excel) :
-
-
Tableau Excel :
-
Dans la cellule
jaune, on tape l’expression : = moyenne (B2 :B21)
-
-
Calcul de la
variance :
-
La variance
var est le quotient de la somme des
carrés des écarts à la moyenne par le nombre
n de l’effectif total.
-
-
var (v) ≈ 4,38
(m / s)2
-
Calcul de
l’écart-type : - L’écart type σn-1 est égal à la racine carrée de la variance.
- L’écart type caractérise la dispersion des
valeurs :
-
- σn-1 ≈ 2,1 m / s
-
Incertitude de
répétabilité associée à la mesure :
-
- L’incertitude de répétabilité dépend du nombre n de mesures indépendantes réalisées,
de l’écart-type de la série
de mesures et du coefficient k appelé facteur
l’élargissement.
-
Ce nombre k
dépend du niveau de confiance choisi et du nombre
n de mesures effectuées.
-
La valeur de k
figure dans un tableau issu de la loi statistique
dite « loi de STUDENT ».
-
Pour un niveau de
confiance de 95 % et pour une série de 20 mesures,
le tableau donne : k = 2,09.
-
-
On en déduit la
valeur de la vitesse des ultrasons dans l’air à 20
°C :
-
v = (339 ± 1)
m / s ou 338 m / s ≤ v ≤ 340 m / s 3)-
Paramètre influençant la vitesse de propagation des
ultrasons dans l’air :
-
La vitesse de
propagation (célérité) dépend de la température. - On admet que la célérité du son (et aussi des ultrasons) dans l’air est proportionnelle
à la racine carrée de la
température absolue T.
-
-
Dans le cas présent :
-
|
VII- Exercice 26 page 54. À chacun son rythme.
|
On souhaite connaître la vitesse d’onde onde ultra sonore. On réalise le montage
ci-dessous :
La base de temps
est fixée à 5,0 μs / div ; les sensibilités
verticales sont identiques. Lorsque les récepteurs sont à
égale distance de l’émetteur, les signaux sont en
phase. Le récepteur R1 restant fixe, on éloigne le récepteur R2 le long de l’axe (Ox) en comptant le nombre de fois
où les signaux sont en phase. Pour une distance d
égale à (8,5 ± 0,1) cm, les signaux ont été dix fois
en phase. On considère que l’incertitude
U (T) sur la mesure de la période est
de 0,20 division. L’incertitude sur la vitesse
est donnée par :
1)- Période : a)-
Calculer la valeur de la période T des
ondes ultrasonores à partir de l’oscillogramme. b)-
Calculer l’incertitude U (T)
sur la période. 2)- Longueur d’onde : a)-
Déterminer la valeur de la longueur d’onde
λ connaissant la distance d. b)-
Quelle est l’incertitude U (λ)
sur la longueur d’onde ? 3)- Relation fondamentale : a)-
Quelle est la relation entre la longueur
d’onde λ et la période T de l’onde ? b)-
Calculer la valeur de la vitesse v de
l’onde ultrasonore et sont incertitude U (v). |
|
1)- Valeur de la période T de l’onde
ultrasonore :
a)-
Valeur de la période T de l’onde
ultrasonore -
T = x . b -
T ≈ 5,0
× 5,0 -
T ≈ 25 μs b)-
Incertitude U (T) sur la valeur
de la période : -
U (T) = 0,20
× 5,0 -
U (T) = 1,0 μs -
On peut écrire que : -
T = (25 ± 1,0) μs 2)- Longueur d’onde : a)-
Valeur de la longueur d’onde : -
Comme pour le déplacement d du
récepteur R2 par rapport au
récepteur R1, les signaux sont en
phase pour la dixième fois : -
On tire que : d = 10 λ
avec d = (8,5 ± 0,1) cm -
b)-
Incertitude U (λ) sur la
longueur d’onde : -
-
On peut écrire : -
λ = (0,85 ± 0,01) cm 3)- Relation fondamentale : a)-
Relation entre la longueur d’onde λ et
la période T de l’onde : -
λ = v . T b)-
Valeur de la vitesse v de l’onde
ultrasonore et sont incertitude U (v) : -
-
Incertitude U (v) : -
-
On peut écrire : -
v = (3,3 ± 0,1)
× 102 m / s |
VIII- Exercice 29 page 55. Accorder une guitare avec un diapason.
|
Lorsque deux notes ont des fréquences
proches, leur mélange produit un son dont
l’intensité varie au cours du temps. Ce phénomène, appelé battement,
peut être utilisé pour accorder la 5ième
corde d’une guitare à l’aide d’un diapason. Cette corde émet normalement un
son dont la fréquence du fondamental est de 110 Hz. Un diapason émet un son pur,
c’est-à-dire un son dont le spectre en fréquences
n’est composé que d’un fondamental. LYA souhaite vérifier la rigueur de cette méthode. Elle enregistre les sons émis simultanément par sa guitare et un diapason et
obtient l’oscillogramme ci-dessous à partir duquel
elle trace le spectre correspondant : 1)-
Repérer sur le spectre les fréquences du fondamental
et des harmoniques de la note émise par la guitare. 2)-
Repérer de même la fréquence de la note émise par le
diapason. 3)-
À l’aide de l’oscillogramme, expliquer la phrase en
italique. 4)-
La corde est-elle accordée ? 5)-
Après avoir modifié la tension de la corde, LYA
réalise une nouvelle acquisition et obtient le
spectre suivant :
-
Quelles sont les
fréquences du fondamental et des harmoniques de la
note émise par la guitare ? 6)-
La corde est-elle accordée ? |
|
1)-
Fondamental et harmoniques :
2)-
Note émise par le diapason : La3 440 Hz. 3)-
Phrase en italique :
-
Lorsque deux notes
ont des fréquences proches, leur mélange produit un
son dont l’intensité varie au cours du temps. - On remarque que l’amplitude de la tension du signal résultant de l’association des deux notes varie au cours du temps. On observe des battements. Ce phénomène s’intensifie lorsque les fréquences des deux notes sont proches.
Le phénomène disparaît lorsque les
fréquences des deux notes sont identiques.
https://fr.wikipedia.org/wiki/Battement
https://fr.wikipedia.org/wiki/Battement#Psychoacoustique_du_battement 4)- Comme on observe des battements, la corde n’est pas accordée (il faut comparer 428 Hz avec 440 Hz). 5)-
Fréquence et fondamental :
6)-
Dans ce cas, la corde est accordée, la fréquence du
fondamental est de 110 Hz et la troisième harmonique
se superpose au son émis par le diapason (440 Hz). |
IX- Exercice 34 page 58. L’oreille humaine en concert.
|
Un ingénieur du son a un rôle primordial pour la sonorisation des salles, en particulier lors d’un concert de musique. À l’aide d’une table de mixage, il règle les sons
qui arrivent depuis les microphones des musiciens et
les renvoie vers les enceintes de façade et de
retour. L’ingénieur intervient sur
quatre qualités des sons : la hauteur, l’intensité,
le timbre et la durée. Grâce à la table de mixage, il convertit facilement un son en un autre. Il peut
notamment modifier un son correspondant à
l’enregistrement 1 en un son correspondant à
l’enregistrement 2. Les différentes représentations
d’un son lui permettent de reconnaître ses
caractéristiques "voir l’enregistrement 3".
Pour régler le
niveau sonore de la salle de concert, l’ingénieur
connaît certaines règles. Par exemple, s’il fait ses réglages pour avoir un son de 98 dB pour des spectateurs situés à 16 m d’une enceinte, il sait
que l’intensité sonore sera quatre fois plus grande
pour les spectateurs situés à 8 m de l’enceinte. Il sait aussi que l’intensité
sonore est doublée s’il place à côté deux enceintes
identiques. Pour ces réglages l’ingénieur
doit tenir compte des seuils de risque, de danger et
de douleur. En effet l’exposition à un niveau sonore trop élevé peut provoquer des acouphènes. L’acouphène est un bourdonnement ou
sifflement parasite qu’une personne entend sans que
ce bruit existe réellement.
Effets du
niveau d’intensité sonore L sur l’oreille humaine. 1)-
Donner la définition de la hauteur d’un son. 2)-
Déterminer la hauteur du son correspondant à
l’enregistrement 1. 3)- Quelle modification a effectué l’ingénieur pour obtenir l’enregistrement 2 ? Quel paramètre du son a
varié entre ces deux enregistrements ? Justifier
votre réponse. 4)-
En utilisant l’analyse spectrale, montrer que la
hauteur du son émis lors de l’enregistrement 3 est
identique à celle des enregistrement 1 et 2. 5)-
Quelle différence présente le son de
l’enregistrement 3 par rapport aux enregistrements 1
et 2 ? Quel paramètre du son est ainsi mis en
évidence ? 6)-
Montrer que l’intensité I1 du son
à 16 m de l’enceinte vaut I1 = 6,3
× 10–3
W / m2. 7)-
Si l’ingénieur place dix enceintes identiques côte à
côte sur la scène, quel est le niveau d’intensité
sonore L2 à 16 m. 8)- Montrer que le niveau d’intensité sonore augmente de 6 dB chaque fois que l’on divise la distance par deux. À partir de quelle distance des enceintes le
son est-il douloureux à écouter ? 9)-
Quels sont les risques auditifs encourus par les
spectateurs qui se placent très près des enceintes ? Donnée :
I0
= 1,0
× 10–12
W / m2 |
|
1)-
Définition de la hauteur d’un son :
-
De façon générale, la
hauteur d’un son est liée à la fréquence f1du
fondamental de ce son.
-
Plus la fréquence
d’un son est faible et plus le son est grave ou bas.
-
Plus la fréquence
d’un son est élevée et plus le son est aigu ou haut. 2)-
Hauteur du son correspondant à l’enregistrement 1 :
-
Fréquence du son :
ici on est en présence d’un son pur
-
3)-
Modification effectuée par l’ingénieur pour obtenir
l’enregistrement 2 : - Pour l’enregistrement 1, l’amplitude de la tension est de 2 V alors que sur l’enregistrement 2,
l’amplitude de la tension
est supérieure à 4 V. L’ingénieur a modifié
l’amplitude de la tension. - En conséquence, l’ingénieur a amplifié le son. - Le son est plus fort alors que la hauteur du son n’a pas changé.
- Il a
modifié l’intensité sonore du son. 4)-
Hauteur du son de l’enregistrement 3 :
-
Le son obtenu est un
son complexe qui possède un fondamental et plusieurs
harmoniques.
-
La fréquence du
fondamental est f1 = 500 Hz.
-
Le son de
l’enregistrement 3 a la même hauteur que celui de
l’enregistrement 2. 5)-
Différence entre le son de l’enregistrement 3 et
celui des enregistrements 1 et 2 : - Le son de l’enregistrement 3 est un son complexe.
- Il comprend
le fondamental f1 = 500 Hz et
plusieurs harmoniques de fréquences 1000Hz, 1500Hz
et 200 Hz - Les sons des enregistrements 1 et 2 sont des sons purs de même fréquence :
- f = 500 Hz.
-
Le son de
l’enregistrement 3 n’a pas le même timbre que les
sons des enregistrements 1 et 2.
-
La perception du son
de l’enregistrement 3 n’est pas la même que celle du
son des enregistrements 1 et 2.
-
Paramètre du son mis
en évidence : On a mis en évidence le timbre d’un
son.
-
Le timbre d’un son
dépend du nombre et de l’amplitude des harmoniques
qui sont présents. 6)-
Valeur de l’intensité I1 du son à
16 m.
-
On donne le niveau
d’intensité sonore à 16 m : L1 =
98 dB
-
D’autre part : I0
= 1,0
× 10–12
W / m2
-
Relation donnant le
niveau d’intensité sonore :
-
On tire :
-
-
Application
numérique :
-
7)-
Niveau d’intensité sonore L2 pour
dix enceintes identiques :
-
Les intensités
sonores s’ajoutent : I2 = 10 I1
-
8)-
Niveau d’intensité sonore et distance :
-
L’intensité sonore
est quatre fois plus grande pour les spectateurs
situés à 8 m que pour les spectateurs situés à 16 m. - Pour les spectateurs situés à 16 m, l’intensité sonore vaut :
- I1
et le niveau d’intensité sonore vaut L1. - Pour les spectateurs situés à 8 m, l’intensité sonore vaut :
- I = 4
I1 et le niveau d’intensité sonore
vaut L.
-
- En conséquence, le niveau d’intensité sonore augmente de 6 dB lorsque la distance séparant
les enceintes des spectateurs
est divisée par deux. 9)-
Distance et son douloureux :
-
Le seuil de la
douleur est Ld = 120 dB
-
À 16m, L2
= 108 dB
-
À 8 m, le niveau
d’intensité sonore est L = 114 dB
-
À 4 m, le niveau
d’intensité sonore est L = 120 dB
-
À 2 m, le niveau
d’intensité sonore est L = 126 dB
-
À 1 m, le niveau
d’intensité sonore est L = 132 dB
-
À 4 m de la scène, le
son est douloureux à écouter. 10)-
Les risques auditifs : - L’effet d’exposition à un niveau sonore trop élevé peut provoquer des acouphènes.
- L’acouphène est un bourdonnement ou
sifflement parasite qu’une personne entend sans que
ce bruit existe réellement.
-
L’exposition à un
niveau sonore trop élevé peut provoquer la surdité
et ce phénomène est irréversible. |
|
|