I- But :

II- Mesure d’un retard pour une salve ultrasonore.

1)- Dispositif expérimental.

Schématiser le montage et le réaliser.

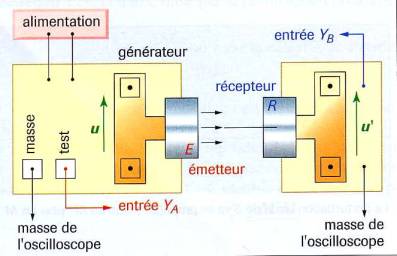
2)- Mesures.

Mettre en place l’émetteur ultrasonore et le récepteur. 

- Observer l’écran de l’oscilloscope lorsque l’émetteur est en mode salve (une salve ultrasonore est une perturbation sonore de fréquence supérieure à 20 kHz séparée par une durée réglable.)

-  Fixer la règle et déplacer le récepteur R pour obtenir sur l’écran de l’oscilloscope la disposition de la figure 1.

-  Placer le zéro de la règle à la position du récepteur R quand l’écran montre la figure 1.

-  Déplacer lentement le récepteur R en observant l’écran jusqu’à ce que le début de la salve soit décalé d’une division. 

-  Lorsque le récepteur R est dans la position de la figure 2, la déformation reçue a un retard τ par rapport à la déformation reçue dans la position de la figure 1.

-  Repérer la position du récepteur sur la règle : d = .

3)- Exploitation.

-  Grâce à la durée de balayage de l’oscilloscope, déduire la valeur du retard τ . 

- À quel parcours des ultrasons le retard t correspond-il ? En déduire la célérité des ultrasons dans l’air. Comparer cette valeur à celle trouvée précédemment. Conclusion.

-  Position du récepteur :

-  Réglages de l’oscilloscope :

-  Retard mesuré à l’aide de l’oscilloscope :

-  Δt = τ = s . x

-  Δt = τ   ≈ 0,500 × 1,00

-  Δt = τ   ≈ 0,500 ms

-  Δt = τ   ≈ 5,00 × 10 ^{– 4}  s

-  Célérité des ultrasons dans l’air :

- 

Pour plus de précision, on peut déplacer le récepteur jusqu’à ce que le début de la salve soit décalé de deux divisions

(cela n’est pas réalisable avec tous les dispositifs, certains sont trop instables).

-  La vitesse de propagation d’une onde sonore ne dépend pas de sa fréquence. 

-  L’air n’est pas un milieu dispersif pour les ondes sonores.

III- Mesure de la longueur d’onde d’une onde ultrasonore.

1)- Dispositif expérimental.

Réaliser le montage suivant et le faire vérifier.

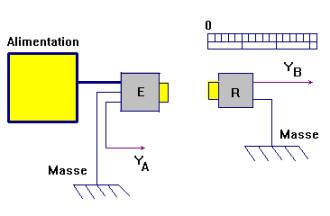
-  Réaliser les réglages afin d’obtenir un oscillogramme exploitable 

-  Il faut régler la durée de balayage pour observer une à deux périodes et la sensibilité verticale pour utiliser les 2/3  de l’écran.

-  Placer l’émetteur E et le récepteur R de façon à ce que les courbes observées à l’oscilloscope soient en phase (R doit être suffisamment proche de E). 

-  Repérer la position initiale de R. déplacer R jusqu’à ce que les courbes se trouvent en phase pour la dixième fois. 

-  On note d le déplacement correspondant du récepteur R.

 2)- Mesures.

Quelle relation existe-t-il entre la longueur d’onde λ et la distance d. En déduire la valeur de la longueur d’onde λ de l’onde ultrasonore ?

-  Relation entre la longueur d’onde λ et la distance d :

-  Comme les courbes sont en phase pour la dixième fois : d = 10 λ 

-  Valeur de la mesure du déplacement d : d ≈ 8,80 cm

-  Longueur d’onde de l’onde ultrasonore : λ ≈ 0,880 cm

-  Indiquer les valeurs choisies pour la durée de balayage et la sensibilité verticale.

-  Durée de balayage ou sensibilité horizontale b = s = 5,00 µs / div

-  Sensibilité verticale : 

-  Voie A ou 1 : k₁ = 2,0 V / div

-  Voie B ou 2 : k₂ = 2,0 V / div à 0,50 V / div

-  Comparer l’allure des deux courbes observées lorsque R s’éloigne de E.

-  Lorsque le récepteur R s’éloigne de l’émetteur E, l’amplitude de la courbe observée à la voie B diminue. 

-  Au cours de la propagation, l’onde sonore est amortie. De l ‘énergie est dissipée lors de la propagation. 

-  Le récepteur ne reçoit qu’une partie de l’énergie émise par l’émetteur.

-  Déterminer la valeur de la période pour chaque onde. En déduire la valeur de la  fréquence pour chaque onde.

-  Le constructeur indique que la fréquence de l’onde ultrasonore émise par l’émetteur est f ≈ 40 kHz.

-  Le résultat est-il compatible avec cette valeur ?

-  Les deux ondes ont la même période T.

-  Durée de balayage ou sensibilité horizontale : b = s = 5,00 µs / div

-  Déplacement horizontal pour une période : x ≈ 5,0 div

-  T = b . x

-  T ≈ 5,00 × 5,0

-  T ≈ 25 µs

-  Fréquence de l’onde ultrasonore :  

- 

-  Comparaison : Le résultat est bien en accord avec la valeur donnée par le fabricant.

-  Donner la température de la salle :  θ = 23,3 ° C

-  Donner la relation fondamentale des ondes mécaniques progressives périodiques.

-  λ = v . T

-  En déduire la valeur de la vitesse des ondes ultrasonores à la température de la salle.

-  Célérité de l‘onde ultrasonore dans l’air à la température θ = 23,3 ° C.

-  Valeur expérimentale de la vitesse : Relation fondamentale :  

- 

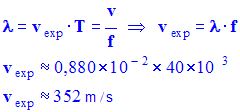
Comparaison avec la valeur théorique. À 0 °C = 273 K, la célérité du son dans l’air est de 331, 45 m / s. 

On admet que la célérité du son dans l’air est proportionnelle à la racine carrée de la température absolue T.

-  Donner la relation liant la vitesse du son à une température donnée T.

-  De l’énoncé, on peut déduire la relation suivante :

- 

- La grandeur T représente ici la température absolue.

- La notation  T₀ représente la température de la salle à 0 ° C et T représente la température de la salle à θ ° C.  

- Méthode 1 : 

-  On peut calculer la valeur de k₁ en utilisant les données :  

- 

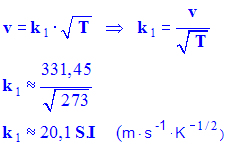
- Méthode 2 : 

-  Relation 1 :

-  Relation 2 :

-  On en déduit la relation suivante :

-     ou .  

-  En déduire la valeur de la vitesse du son v_th à la température de la salle.

-  Valeur théorique de la vitesse à  la température θ = 23,3 ° C :

-  Célérité de l‘onde ultrasonore dans l’air à la température θ = 23,3 ° C.

-  Valeur théorique de la vitesse à 23,3 ° C :  

- 

-  Comparer la valeur expérimentale avec la valeur théorique. Conclusion.

-  Comparaison :

- 

-  La valeur expérimentale est proche de la valeur théorique. 

-  L’air n’est pas un milieu dispersif pour les ondes sonores.