|
Chap. N° 03 |
Propriétés des ondes. Cours. |
|
 |
|
Exercices : énoncé avec correction a)- Exercice 6 page 76 :
Connaître le phénomène de diffraction. b)- Exercice 9 page 76 :
Connaître le phénomène d’interférences. c)- Exercice 13 Page 76 :
Comparer des fréquences. d)- Exercice 15 page 77 :
Largeur d’une tache centrale. e)- Exercice 17 page 77 :
Mailles du voilage.
f)- Exercice 24 Page 80 :
Calcul d’une longueur d’onde. |
1)- Observation avec des ondes
lumineuses.
a)-
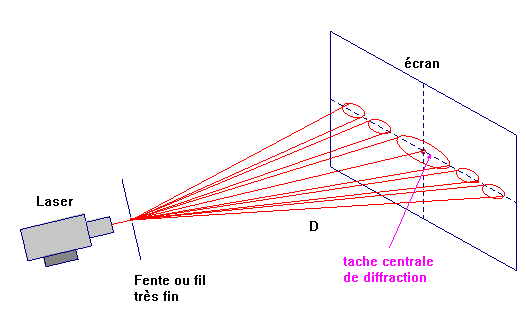
Expérience :
|
|
|
|
|
|
|
Schéma du
montage
|
|
|
Observations :
|
|
|
|
|
|
|
|
-
Vidéos : diffraction par une fente
►Observations :
-
Lorsque la fente est large, environ 2 mm, le faisceau
laser n’est pratiquement pas modifié.
-
On diminue la largeur de la fente.
- Lorsque la largeur de la fente est inférieure à 1 mm, on observe sur l’écran un étalement du faisceau laser perpendiculairement à la fente.
- Cet étalement de la lumière est
appelé figure de diffraction.
-
Elle est constituée d’une tache centrale et de taches
secondaires situées symétriquement par rapport à la tache
centrale.
- La tache centrale est très lumineuse et deux fois plus large que les autres taches.
- La luminosité diminue très vite
lorsqu’on s’éloigne de la tache centrale.
-
La fente a diffracté la lumière dans une direction
perpendiculaire à celle de la fente.
-
La diffraction est d’autant plus marquée que la largeur
de la fente est petite.
b)-
Écart angulaire :
-
L’écart angulaire est l’angle sous lequel est vue la
moitié de la tache centrale depuis l’objet diffractant.
-
C’est le demi-diamètre angulaire de la tache centrale.
-
Schéma :
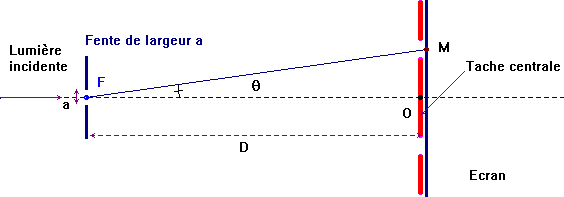
- F : milieu de la fente. O milieu de la tache centrale.
- M milieu de la première extinction.
- D
est très grand devant OM.
- Lorsqu’un faisceau parallèle de lumière de longueur d’onde λ traverse une fente de largeur a,
- l’écart angulaire
θ, entre le centre
de la tache centrale et la première extinction est donné par la
relation :
-
-
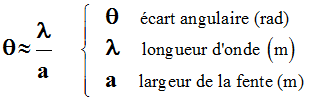
Cette relation permet de déterminer expérimentalement la
longueur d’onde λ de la lumière d’un faisceau connaissant
la largeur de la fente.
- Dans le cas ou D >> L, on peut déterminer la relation donnant la largeur de la tache centrale en fonction de la longueur d’onde λ et de la largeur de la fente.
- On
fait l’approximation des petits angles.
-
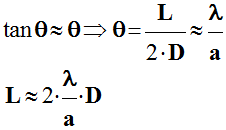
2)- La diffraction dans différentes
situations.
-
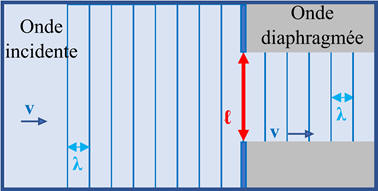
Le phénomène de diffraction peut s’observer aussi bien
avec les ondes électromagnétiques qu’avec les ondes mécaniques.
-
C’est grâce au phénomène de diffraction que l’on a mis en
évidence le caractère ondulatoire de la lumière.
-
Exemples :
-
Le phénomène de diffraction dépend des dimensions de
l’ouverture ou de l’obstacle.
-
Ce phénomène se manifeste si les dimensions de
l’ouverture ou d’un obstacle sont du même ordre de grandeur que
la longueur d’onde λ.
-
L’onde diffractée a même fréquence
f et même
longueur d’onde λ que l’onde incidente.
-
Pour une longueur d’onde
λ donnée, le phénomène de
diffraction est d’autant plus marqué que la dimension de
l’ouverture ou de l’obstacle est plus petite.
Expérience :
-
On produit des ondes rectilignes grâce à la cuve à onde
et on observe ce qui se passe lorsque ces ondes rectilignes
rencontrent une ouverture.
-
Lorsque l’ouverture est grande, les ondes rectilignes
sont peu affectées lors du passage de celle-ci.
-
Lorsque l’ouverture devient plus petite, on observe une
modification de l’onde rectiligne après le passage de
l’ouverture.
-
On a mis en évidence le phénomène de diffraction.
-
Ce phénomène est caractéristique des ondes.
-
L’onde qui arrive sur l’ouverture est appelée :
onde
incidente et l’onde après l’ouverture est appelée
onde
réfractée.
-
Images et schémas :
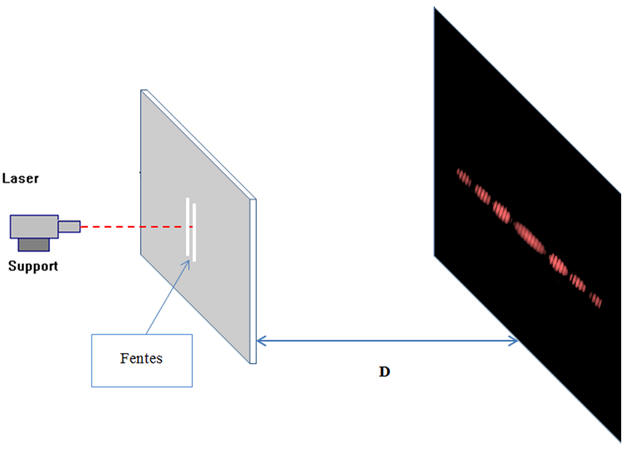
1)- Interférences en lumière
monochromatique.
Expérience de Young.
|
|
La tache centrale de diffractionest striée de fines bandes rectilignes rouges, parallèles et équidistantes.
|
|
|
|
-
Au phénomène de diffraction se superpose le phénomène
d’interférence.
-
L’ensemble des franges alternativement brillantes
(rouges) et sombres constitue des franges d’interférences.
-
La distance entre deux franges sombres ou
brillantes (rouges) est la même.
-
On l’appelle l’interfrange, noté
i.
2)- Interférences avec les
ultrasons.
Expérience avec les ultrasons :
-
On utilise les ultrasons pour mettre en évidence ce
phénomène qui est caractéristique des ondes.
-
Dispositif expérimental :
- Première étape : Seul l’émetteur E1 est en marche.
-
On déplace le récepteur R.
-
Lorsque l’on éloigne le récepteur
R, les courbes
se décalent l’une par rapport à l’autre.
-
Lorsque les courbes sont en phase, cela veut dire que les
points E1 et
R sont dans le même état
vibratoire.
-
Pour que les courbes soient de nouveau en phase, il faut
déplacer le récepteur de la distance d
égale à une
longueur d’onde λ.
- Deuxième étape : Seul l’émetteur E2 est en marche.
- On déplace le récepteur R.
-
Idem.
-
Troisième étape : Les deux émetteurs
E1
et E2 sont en marche.
-
On déplace le récepteur R le long d’une droite
perpendiculaire à (E1, E2).
-
On constate qu’en certains points, l’amplitude du signal
reçu est maximale et qu’en d’autres points, l’amplitude du
signal reçu est minimale.
-
Si on place le récepteur à un endroit ou l’amplitude est
maximale et que l’on arrête E2, on remarque
que la vibration émise par E1
est en phase
avec celle reçue par le récepteur R.
- On recommence, mais maintenant, on arrête E1.
- On fait la même remarque.
-
En conséquence, lorsque l’amplitude est maximale, les
vibrations émises par E1 et E2 arrivent au récepteur en phase : elles ajoutent leurs
effets.
-
Quatrième étape : On place le récepteur
R
en un point ou l’amplitude est minimale.
-
Idem.
-
Lorsque l’amplitude est minimale, les vibrations sont en
opposition de phase : elles annulent leurs effets.
-
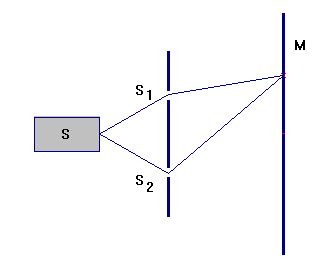
Différence de marche et chemin optique :
-
On définit le chemin optique comme le produit de l’indice
n du milieu de réfraction par la distance
e parcourue par le rayon lumineux dans le milieu. :
-
Le chemin optique (d) =
n . e
-
La différence de marche
δ entre 2 ondes est égale
à la différence de leur chemin optique :
-
δ = (d2)
– (d1)
= n2 . e2 – n1
. e1
-
Avec : (d1) =
n . (SS1
+ S1M)
-
Et : (d2) =
n . (SS2
+ S2M)
-
Avec n = 1, on écrit : δ = |(SS2
+ S2M)
– (SS1 +
S1M)|
|
|
Si les deux rayons lumineux se déplacent dans le même milieu d’indice n, il existe une différence de
chemin optique entre les deux rayons.
On parle de différence de
marche δ. Il existe entre les deux ondes lumineuses arrivant en
M une différence de
marche δ. δ = |(SS2
+
S2M)
–
(SS1
+ S1M)| |
-
Si δ
= k . λ,
-
Les deux ondes arrivent au point
M en phase et
elles ajoutent leurs effets.
-
On dit que l’interférence est constructive.
-
On obtient une frange brillante.
-
Si,
-
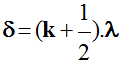
Les deux ondes arrivent au point
M en opposition
de phase et elles annulent leurs effets.
-
On dit que l’interférence est destructive.
-
On obtient une frange sombre.
4)- Nécessité de sources cohérentes.
-
pour
obtenir des interférences, les sources doivent être cohérentes.
-
Elles doivent être synchrones et présenter un déphasage
constant.
-
En optique deux sources lumineuses indépendantes ne sont
jamais cohérentes.
-
C’est pour cela que pour observer des franges
d’interférences, on utilise deus sources secondaires obtenues à
partir d’une source unique de petite dimension.
-
Les faisceaux émis par 2 sources indépendantes ne
peuvent pas interférer.
-
On réalise 2 sources mutuellement cohérentes en
éclairant 2 fentes avec un faisceau émis par une source primaire
de petite dimension ou avec un faisceau laser.
-
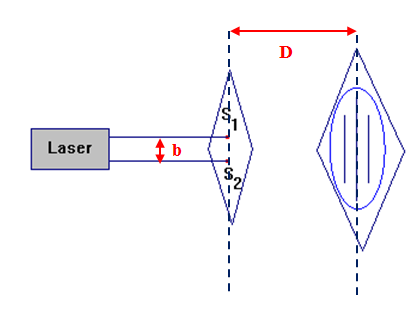
Lors d’interférences lumineuses, l’interfrange, notée
i, est la distance séparant deux franges brillantes
consécutives ou deux franges sombres consécutives.
-
Dans le cas des fentes de Young, pour une lumière
monochromatique de longueur d’onde λ :
-
Expression de l’interfrange :
-
Schéma :
-
-
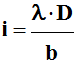
La mesure de la valeur de l’interfrange
i permet
de déterminer la valeur de la longueur d’onde
λ de la
lumière monochromatique utilisée.
6)- Interférence en lumière blanche.
-
Les couches minces, constituées d’huile, d’essence, les
bulles de savon, les DVD, éclairés en lumière blanche font
apparaître des irisations colorées.
-
Les ondes lumineuses sont réfléchies sur les parois
interne et externe de telles couches et elles peuvent
interférer.
-
Chaque radiation de longueur d’onde
λ donne sa
propre figure d’interférences.
-
La superposition des différentes figures d’interférences
conduit à l’observation de zones colorées.
-
Les couches minces éclairées en lumière blanche font
apparaître des couleurs interférentielles.
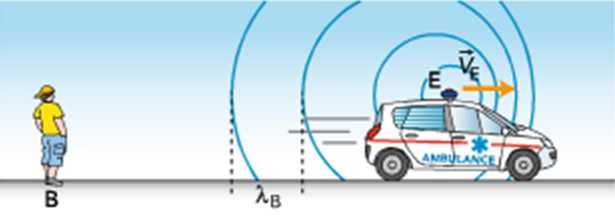
- Une onde électromagnétique ou mécanique émise avec une fréquence fE est perçue avec une fréquence différente fR lorsque l’émetteur et le récepteur sont en déplacement relatif.
- C’est ce que l’on appelle
l’effet Doppler.
-
Exemple :
-
Le son d’une sirène est perçu plus aigu lorsque le
véhicule qui l’émet s’approche de l’observateur.
-
Le son de la sirène est plus grave lorsque le véhicule
qui l’émet s’éloigne de l’observateur.
-
Ce phénomène a été prévu par C. DOPPLER en 1842 et
confirmé expérimentalement en 1845 par C. BUYS-BALLOT.
2)- Vitesse relative d’un émetteur
par rapport à un récepteur.
-
L’effet Doppler constitue une méthode de mesure des
vitesses.
b)-
Détermination par effet Doppler de la vitesse d’un
émetteur sonore qui s’approche (exercice 27 page 81) :
La valeur de la vitesse d’un émetteur
E
s’approchant d’un observateur immobile (A) peut être
calculée par effet Doppler.
- On se propose de retrouver la
relation liant les diverses grandeurs mises en jeu :
-
fE est la fréquence du signal produit
par l’émetteur ;
-
fA est la fréquence du signal reçu par
l’observateur ;
-
V est la valeur de la vitesse de l’onde ;
-
VE est la valeur de la vitesse de
l’émetteur par rapport à l’observateur.
-
Les valeurs des vitesses sont mesurées dans un
référentiel terrestre :
-
On se place dans le cas où :
-
L’air est supposé immobile par rapport au son.
-
La vitesse de déplacement de l’émetteur par rapport au
récepteur est faible et inférieure à la vitesse de l’onde dans le
milieu de propagation.
-
En conséquence, on considère que :
VE
<< V
-
Schéma représentatif de la situation :
À
la date t0 = 0 s,
E est à la distance
d de
A et émet une onde.
- Exprimer littéralement la
date t1 au bout de laquelle le signal est
perçu par A.
-
Expression de la date
t1 :
-
L’onde est émise de l’émetteur (E) se déplace à la
vitesse V.
-
La distance parcourue par l’onde est
d.
-
Date t1 au bout de laquelle le signal
est perçu par A :
-
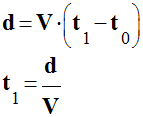
Déterminer
l’expression de la distance dE parcourue par
l’émetteur (E) pendant la période
TE du
signal émis.
-
Expression de la distance
dE parcourue
par l’émetteur (E) pendant la période
TE
du signal émis :
-
L’émetteur se déplace à la vitesse
VE
par rapport à l’observateur :
-
dE =
VE .
TE
À
la date TE, quelle est la distance
d’
entre E et
A ?
-
À la date TE, l’émetteur a parcouru la
distance dE. L’émetteur se rapproche de
A.
-
d’ =
d –
dE
-
d’ =
d –
VE .
TE
À
la date TE, l’émetteur émet de nouveau une
onde.
- À quelle date t2 l’observateur reçoit-il
cette onde ?
-
Distance à parcourir :
-
d’ =
d –
VE .
TE
-
Date t2 où l’observateur reçoit cette
onde :
-
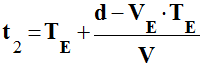
Quelle
est la durée TA séparant deux signaux
consécutifs captés par l’observateur ? Que représente
TA ?
-
Durée TA séparant deux signaux
consécutifs captés par l’observateur,
-
TA =
t2 –
t1
-
-
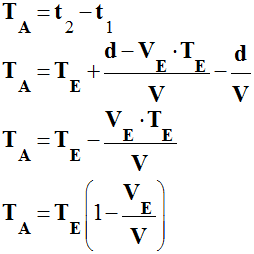
La grandeur TA représente la période de
l’onde perçue par l’observateur.
Exprimer
la relation liant fA,
fE,
V et
VE dans cette situation.
-
Relation liant
fA,
fE,
V et
VE:
-
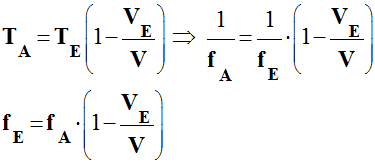
Quelle
est l’expression littérale de la valeur de la vitesse
VE
de l’émetteur ?
-
Expression littérale de la valeur de la vitesse
VE
de l’émetteur :
-
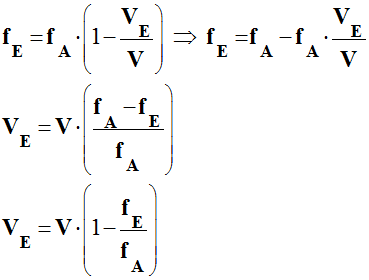
c)-
Détermination par effet Doppler de la vitesse d’un
émetteur sonore qui s’éloigne :
La valeur de la vitesse d’un émetteur
E
s’éloignant d’un observateur immobile (B) peut être
calculée par effet Doppler.
- On se propose de retrouver la
relation liant les diverses grandeurs mises en jeu :
-
fE est la fréquence du signal produit
par l’émetteur ;
-
fB est la fréquence du signal reçu par
l’observateur ;
-
V est la valeur de la vitesse de l’onde ;
-
VE est la valeur de la vitesse de
l’émetteur par rapport à l’observateur.
-
Les valeurs des vitesses sont mesurées dans un
référentiel terrestre :
-
On se place dans le cas où :
-
L’air est supposé immobile par rapport au son.
-
La vitesse de déplacement de l’émetteur par rapport au
récepteur est faible et inférieure à la vitesse de l’onde dans le
milieu de propagation.
-
En conséquence, on considère que :
VE
<< V
-
Schéma représentatif de la situation :
À
la date t0 = 0 s,
E est à la distance
d de
B et émet une onde.
- Exprimer littéralement la
date t1 au bout de laquelle le signal est
perçu par B.
-
Expression de la date
t1 :
-
L’onde est émise de l’émetteur (E) se déplace à la
vitesse V.
-
La distance parcourue par l’onde est
d.
-
Date t1 au bout de laquelle le signal
est perçu par B :
-
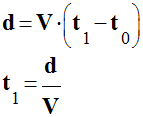
Déterminer
l’expression de la distance dE parcourue par
l’émetteur (E) pendant la période
TE du
signal émis.
-
Expression de la distance
dE parcourue
par l’émetteur (E) pendant la période
TE
du signal émis :
-
L’émetteur se déplace à la vitesse
VE
par rapport à l’observateur :
-
dE =
VE .
TE
À
la date TE, quelle est la distance
d’
entre E et
B ?
-
À la date TE, l’émetteur a parcouru la
distance dE. L’émetteur s’éloigne de B.
-
d’ =
d +
dE
-
d’ =
d +
VE .
TE
À
la date TE, l’émetteur émet de nouveau une
onde. À quelle date t2 l’observateur reçoit-il
cette onde ?
-
Distance à parcourir :
-
d’ =
d +
VE .
TE
-
Date t2 où l’observateur reçoit cette
onde :
-
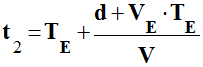
Quelle
est la durée TB séparant deux signaux
consécutifs captés par l’observateur ? Que représente
TB ?
-
Durée TB séparant deux signaux
consécutifs captés par l’observateur.
-
TB =
t2 –
t1
-
-
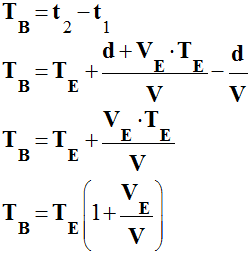
La grandeur TB représente la période de
l’onde captée l’observateur.
Exprimer
la relation liant fB,
fE,
V et
VE dans cette situation.
-
Relation liant
fB,
fE,
V et
VE:
-
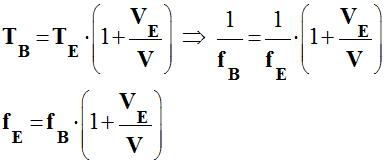
Quelle
est l’expression littérale de la valeur de la vitesse
VE
de l’émetteur ?
-
Expression littérale de la valeur de la vitesse
VE
de l’émetteur :
-
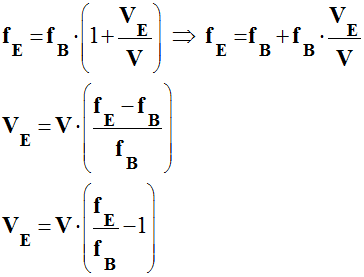
d)-
Une autre approche de l’effet Doppler (avec la longueur
d'onde):
►Émetteur sonore qui s’approche du récepteur :
-
La valeur de la vitesse d’un émetteur
E
s’approchant d’un observateur immobile (A) peut être
calculée par effet Doppler
-
fE est la fréquence du signal produit
par l’émetteur ;
-
λE est la longueur d’onde du son émis
par l’émetteur
-
fA est la fréquence du signal reçu
(perçu) par l’observateur ;
-
λA est la longueur d’onde du son reçu
(perçu) par l’observateur ;
-
V est la valeur de la vitesse de l’onde ;
-
VE est la valeur de la vitesse de
l’émetteur par rapport à l’observateur.
-
Les valeurs des vitesses sont mesurées dans un
référentiel terrestre :
-
On se place dans le cas où :
-
L’air est supposé immobile par rapport au son.
-
La vitesse de déplacement de l’émetteur par rapport au
récepteur est faible et inférieure à la vitesse de l’onde dans le
milieu de propagation.
-
En conséquence, on considère que :
VE
<< V
-
Schéma représentatif de la situation :
-
Au temps t = 0 s, l’émetteur émet le bip 1de
fréquence fE
-
Au temps t =
TE, l’émetteur émet
le bip 2 de fréquence fE.
-
Pendant la durée TE, l’émetteur s’est
rapproché de la distance d :
-
d =
VE.TE
-
Les deux bips sont séparés de la distance
d’ :
-
d’ =
V.TE –
VE.TE
-
La distance d’ représente la longueur d’onde du
signal perçu par l’observateur
-
λA =
V.TE –
VE.TE
-
D’autre part :
-
λE =
V.TE
-
On tire :
-
λA =
λE –
VE.TE
-
L’onde perçue par le récepteur a une longueur d’onde
inférieure (une période inférieure ou une fréquence plus grande)
que celle envoyée par l’émetteur.
-
Expression de la vitesse
VE dans ce cas
:
-
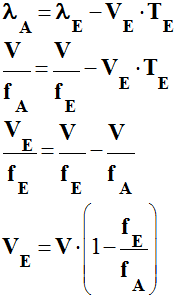
►Émetteur sonore qui s’éloigne du récepteur :
-
La valeur de la vitesse d’un émetteur
E
s’éloignant d’un observateur immobile (B) peut être
calculée par effet Doppler.
-
fE est la fréquence du signal produit
par l’émetteur ;
-
fB est la fréquence du signal reçu par
l’observateur ;
-
V est la valeur de la vitesse de l’onde ;
-
VE est la valeur de la vitesse de
l’émetteur par rapport à l’observateur.
-
Les valeurs des vitesses sont mesurées dans un
référentiel terrestre :
-
On se place dans le cas où :
-
L’air est supposé immobile par rapport au son.
-
La vitesse de déplacement de l’émetteur par rapport au
récepteur est faible et inférieure à la vitesse de l’onde dans le
milieu de propagation.
-
En conséquence, on considère que :
VE
<< V
-
Schéma représentatif de la situation :
-
Au temps t = 0 s, l’émetteur émet le bip 1de
fréquence fE
-
Au temps t =
TE, l’émetteur émet
le bip 2 de fréquence fE.
-
Pendant la durée TE, l’émetteur s’est
éloigné de la distance d :
-
d =
VE.TE
-
Les deux bips sont séparés de la distance d’ :
-
d’ =
V.TE +
VE.TE
-
La distance d’ représente la longueur d’onde du
signal perçu par l’observateur
-
λB =
V.TE +
VE.TE
-
D’autre part :
-
λE =
V.TE
-
On tire :
-
λB =
λE +
VE.TE
-
L’onde perçue par le récepteur a une longueur d’onde plus
grande (une période supérieure ou une fréquence plus petite) que
celle envoyée par l’émetteur.
-
Expression de la vitesse
VE dans ce cas
:
-
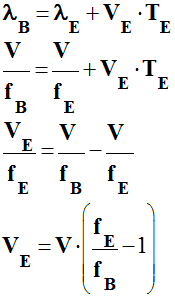
3)- L’effet Doppler-Fizeau en
astronomie.
Le spectre de la lumière émise par une étoile
comporte des raies d’absorption caractéristiques des éléments
présents dans l’atmosphère qui l’entoure.
En appliquant les conséquences de l’effet C.
Doppler à la lumière, H. Fizeau (1819-1896) a postulé en
1848 que :
-
Si une étoile s’éloigne ou s’approche de la Terre, on
doit observer un décalage de ses raies d’absorption.
-
La mesure de ce décalage permettrait de calculer la
vitesse radiale de l’étoile.
Les télescopes modernes et les outils
informatiques permettent aujourd’hui de calculer les vitesses
radiales des étoiles en analysant de très nombreuses raies.
-
L’effet Doppler-Fizeau permet de calculer la valeur de la
vitesse radiale d’une étoile en comparant les longueurs d’onde
de son spectre d’absorption à celles d’un spectre de référence.
-
Lorsque l’étoile s’éloigne de la Terre, on observe un
décalage vers les grandes longueurs d’onde c’est-à-dire vers le
rouge pour les raies du visible (redshift).
-
Lorsque l’étoile se rapproche de la Terre, on observe un
décalage vers les petites longueurs d’onde c’est-à-dire vers le
bleu pour les raies du visible (blueshift).
-
Remarque : la vitesse radiale d’une étoile est la vitesse
à laquelle elle s’éloigne ou s’approche de la Terre.
2)- Exercices :
|
Exercices : énoncé avec correction a)- Exercice 6 page 76 :
Connaître le phénomène de diffraction. b)- Exercice 9 page 76 :
Connaître le phénomène d’interférences. c)- Exercice 13 Page 76 :
Comparer des fréquences. d)- Exercice 15 page 77 :
Largeur d’une tache centrale. e)- Exercice 17 page 77 :
Mailles du voilage.
f)- Exercice 24 Page 80 :
Calcul d’une longueur d’onde. |
|
|