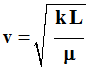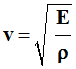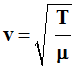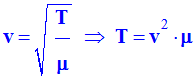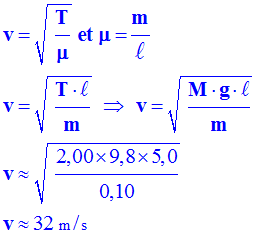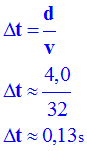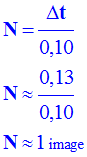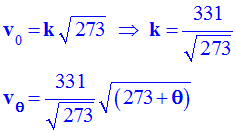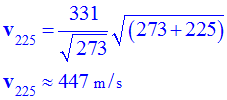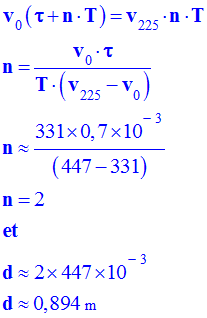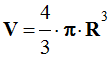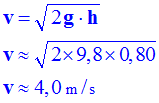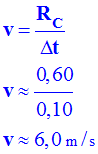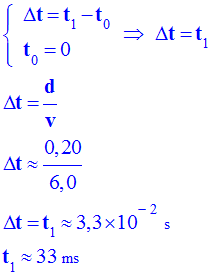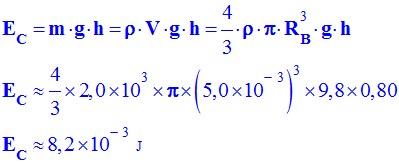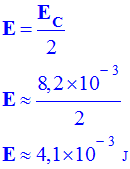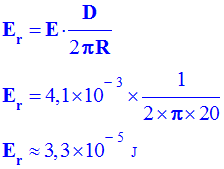|
Phys. N° 01 |
Les Ondes Mécaniques. Exercices |
|
|
|
|
Programme 2012 : Propriétés des Ondes Programme 2020 : Physique et Chimie |
|
QCM N° 01 et N° 02 |
|
5)- La célérité d’une onde longitudinale dans un ressort est donnée par la formule : -
- avec k raideur du ressort, - L sa longueur et - μ sa masse par unité de longueur. - Quelle est l’unité de
k ?
6)- La célérité d’une onde longitudinale dans un barreau est donnée par la formule : - - avec ρ masse volumique du barreau et - E module d’Young. - Quelle est l’unité de
E ?
7)-
Une onde se propage le long d’une corde tendue avec une
célérité de L’origine des temps est prise à l’instant où la perturbation commence en
O, extrémité de la corde. a)-
Un point situé sur la corde à la
distance 1 m de O est en mouvement à la date 0,1 s. b)-
Un point situé sur la corde à la distance c)-
Les points de la corde se déplacent
avec une vitesse égale à la célérité de l’onde. d)-
Les points de la corde ont un
déplacement très petit autour de leur position d’équilibre. 8)-
Une onde sonore se propage dans l’air entre la membrane
d’un haut-parleur et l’oreille d’une personne. a)-
L’onde sonore est une onde
transversale. b)-
Des molécules contenues dans l’air se
déplacent du haut-parleur à l’oreille. c)-
La variation de pression due à l’onde
est très faible. d)-
La célérité du son augmente si la
température augmente. |
|
5)- La célérité d’une onde longitudinale dans un ressort est donnée par la formule : -
- avec k raideur du ressort, - L sa longueur et - μ sa masse par unité de longueur. - Quelle est l’unité de
k ?
- Réponse
: d)-
kg.s– 2. 6)- La célérité d’une onde longitudinale dans un barreau est donnée par la formule : - - avec ρ masse volumique du barreau et - E module d’Young. - Quelle est l’unité de
E ?
- Réponse :
d)- kg.s– 2.m– 1. 7)-
Une onde se propage le long d’une corde tendue avec une célérité de
L’origine des temps est prise à l’instant où la perturbation commence en
O, extrémité de la corde. a)-
Un point situé sur la corde à la
distance 1 m de O est en mouvement à la date 0,1 s. b)-
Un point situé sur la corde à la distance c)-
Les points de la corde se déplacent
avec une vitesse égale à la célérité de l’onde. d)-
Les points de la corde ont un
déplacement très petit autour de leur position d’équilibre. - Réponses :
a)- et d)-. 8)-
Une onde sonore se propage dans l’air entre la membrane d’un haut-parleur et l’oreille d’une personne. a)-
L’onde sonore est une onde
transversale. b)-
Des molécules contenues dans l’air se
déplacent du haut-parleur à l’oreille. c)-
La variation de pression due à l’onde
est très faible. d)-
La célérité du son augmente si la
température augmente. - Réponses :
c)- et d)-. - Remarque : - La célérité du son dans l’air est proportionnelle à la racine carrée à la température absolue T : - |
|
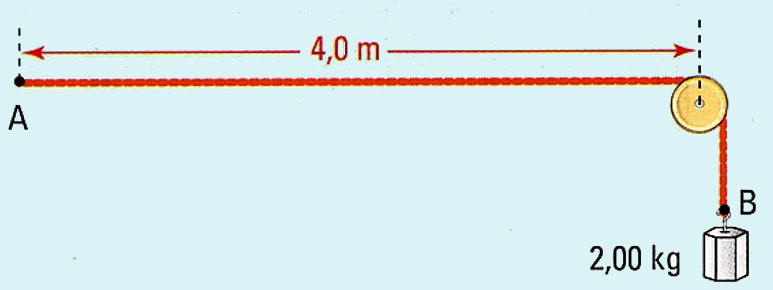
On attache une masse de
puis on crée une déformation à son extrémité A.
La célérité des ondes le long de la corde est donnée par :
-
Avec T tension de la corde et μ masse par unité de
longueur.
On prend : g = 10 N / kg. 1)-
Montrer que la tension T
peut s’exprimer en kg.m.s– 2. 2)-
Quels sont les facteurs liés à la structure de la corde
qui expliquent cette formule ? 3)-
Quelle est la nature des ondes le long de la corde ? 4)-
Calculer la célérité de ces ondes si la masse de la corde
vaut 1,0
x 10 5)-
On filme l’expérience avec une caméra enregistrant à une
vitesse de 10 images par seconde. - Combien d’images montreront la propagation
de la déformation avant que celle-ci n’atteigne la poulie ? |
|
On attache une masse de
puis on crée une déformation à son extrémité A.
La célérité des ondes le long de la corde est donnée par :
-
Avec T tension de la corde et μ masse par unité de
longueur.
On prend : g = 10 N / kg. 1)-
Montrer que la tension T
peut s’exprimer en kg.m.s– 2.
- Une méthode de résolution. - Pour résoudre ce type
d’exercice, on peut adopter la méthode et les notations suivantes. - La notation suivante : [v]
représente la grandeur physique vitesse. - La notation suivante (m.s–1)
représente l’unité de la vitesse. - On écrit l’égalité suivante : [v]
= (m.s–1)
- Cette écriture signifie que la vitesse
s’exprime en mètre par seconde dans le système
S.I. - Pour répondre à la question
posée, on utilise les notations suivantes :
- Unité : - La tension
de la corde s’exprime en newton, symbole N. - Comme le
poids d’un objet sur Terre. - En
conséquence : - [T] =[P]
= [m] . [g]
= (kg) . (m.s–2) - [T] =[P]
= (N) = (kg.m.s–2)
- D’autre
part : en utilisant la formule :
-
- [T] =[v2]
. [μ] = (m2.s–2)
. (kg.m–1)
- [T] = (kg. m.s–2) 2)- Quels sont les facteurs liés à la structure de la corde qui expliquent cette formule ? - Facteurs
liés à la structure de la corde : - La tension
T est liée à la rigidité.
- Plus la
tension est grande, plus la rigidité est grande et plus la célérité est
grande (la tension intervient au numérateur). -
Et
μ est liée à l’inertie.
- Plus la
masse linéique est grande, plus l’inertie est grande et plus la célérité
est petite (la masse linéique intervient au dénominateur). 3)-
Quelle est la nature des ondes le long de la corde ? - On est en
présence d’une onde progressive transversale. 4)-
Calculer la célérité de ces ondes si la masse de la corde
vaut 1,0 x 10 - Célérité de
l’onde : - 5)-
On filme l’expérience avec une caméra enregistrant à une
vitesse de 10 images par seconde. - Combien d’images montreront la propagation
de la déformation avant que celle-ci n’atteigne la poulie ?
- Durée du parcours : -
- Nombre d’images : - - Si on filme
le phénomène, on aura une image !!! |
|
On réalise un montage en mettant en série un générateur d’impulsions, un
haut-parleur, un microphone,
un oscilloscope.
La température du milieu entre le microphone et le
haut-parleur, égale à
0 ° C, peut être modifiée.
La célérité du son dans l’air à cette température est
de
On rappelle que sa valeur est proportionnelle à
la racine carrée de la
température absolue de l’air.
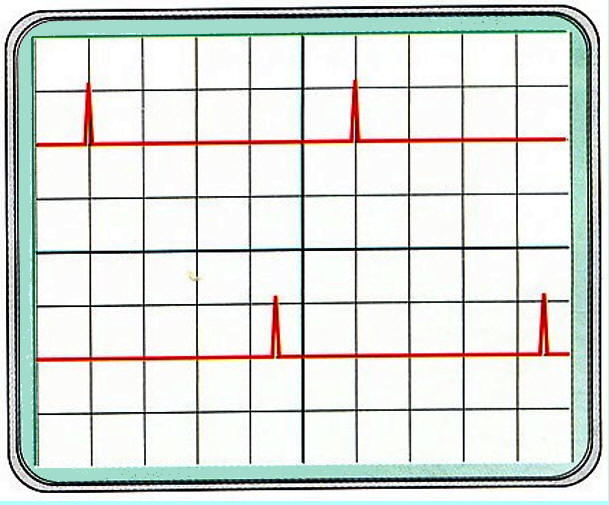
On visualise à l’oscilloscope les tensions aux bornes
du haut-parleur
(voie A, vers le haut) et
du microphone (voie B, vers le
bas).
Le balayage est réglé sur la valeur s = 0,20 ms / div. 1)- Quelle est la périodicité des impulsions ? Quelle
relation le temps mis par le son pour aller du haut-parleur au
microphone vérifie-t-il ? 2)-
Quelles sont les distances possibles entre le
haut-parleur et le microphone ? 3)- On augmente progressivement la température ente le microphone et le haut-parleur jusqu’à ce que les signaux observés sur les deux voies soient en phase. On relève alors une température de 225 ° C. Quelle est la nouvelle valeur de la célérité du son ? Quelle relation
le temps mis par le son pour aller du haut-parleur au microphone
vérifie-t-il ? 4)-
En déduire la distance entre haut-parleur et microphone. |
|
On réalise un montage en mettant en série un générateurd’impulsions, un
haut-parleur, un microphone,
un oscilloscope. La température du milieu entre le microphone et le haut-parleur, égale à 0 ° C, peut être modifiée.
La célérité du son dans l’air à cette température
est de
On rappelle que sa valeur est proportionnelle à
la racine carrée de la
température absolue de l’air.
On visualise à l’oscilloscope les tensions aux bornes
du haut-parleur
(voie A, vers le haut)
et du microphone (voie B, vers le
bas).
Le balayage est réglé sur la valeur s = 0,20 ms / div. 1)- Quelle est la périodicité des impulsions ? Quelle
relation le temps mis par le son pour aller du haut-parleur au
microphone vérifie-t-il ? - Périodicité
des impulsions : - La sensibilité horizontale (ou balayage) : -
s
= 0,20 ms / div, - Le déplacement horizontal pour une période -
T
est x = 5,0 div. - T
= 1,0 ms. - Relation vérifiée
par le temps (durée : Δt) - On note
d la distance séparant le
H.P du micro, - v
la célérité du son et - Δt,
la durée du parcours. - d
= v
. Δt - Cette relation
n’est pas utile pour le moment car on ne connaît pas la distance
d entre le H.P et le micro. - étude de
l’oscillogramme : - Les deux
signaux sont décalés de 3,5 div. - Mais
l’oscillogramme ne permet pas de déterminer directement
Δt.
- Le décalage dans
le temps est connu à un nombre entier n
de périodes T. - On peut
écrire que : - Δt
(ms) = 3,5 x
0,20 + n.T
- Δt
(ms) = 0,70 + n. 2)-
Quelles sont les distances possibles entre le
haut-parleur et le microphone ? - Valeur des
distances possibles. - d
(m)
=
v . Δt
- d
= 331
x 0,70
x 10– 3
+331 n
x 10– 3
- d
(m)
= 0,232 + 0,331
n.
3)- On augmente progressivement la température ente le microphone et le haut-parleur jusqu’à ce que les signauxobservés sur les deux voies soient en phase. On relève alors une température de 225 ° C. Quelle est la nouvelle valeur de la célérité du son ? Quelle relation
le temps mis par le son pour aller du haut-parleur au microphone
vérifie-t-il ? - Célérité du
son : - On rappelle
que sa valeur est proportionnelle à la racine carrée de la température
absolue de l’air. - - à
partir de la valeur de
la célérité du son à 0 ° C,
on peut déterminer la valeur de la constante
k. - - Valeur de la
célérité du son à 225 ° C : - - Comme la
célérité augmente, la durée diminue : - Δt'
≤ Δt. - Les deux
signaux sont en phase : - Δt'
(ms) = n . T 4)-
En déduire la distance entre haut-parleur et microphone. - Distance
entre le H.P et le micro. - Relation (1) :
d =
v0
(τ +
n . T)
- Relation (2) :
d =
v225
. n .
T
- En
conséquence : -
|
IV-
Exercice 26 page 44. Chute dans l’eau.
|
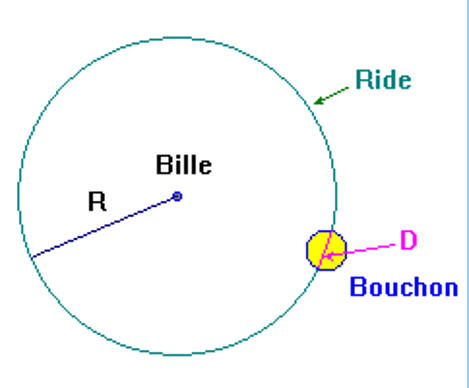
Une petite bille tombe dans une cuvette cylindrique remplie
d’eau de
rayon
La bille est initialement à
On néglige les frottements de l’air.
L’origine des temps est prise à l’instant du contact avec l’eau.
Le niveau de référence pour l’énergie potentielle est la surface
de
l’eau.
Le rayon de la bille est de
On prend : g = 9,8 N / kg. Le volume d’une sphère est :
-
1)-
En utilisant le cours de première
S, calculer la vitesse de la
bille à l’instant où elle touche l’eau. 2)- Au moment de l’impact, la bille perd la moitié de son énergie. De quel type d’énergie s’agit-il ?
Que
devient-elle ? 3)-
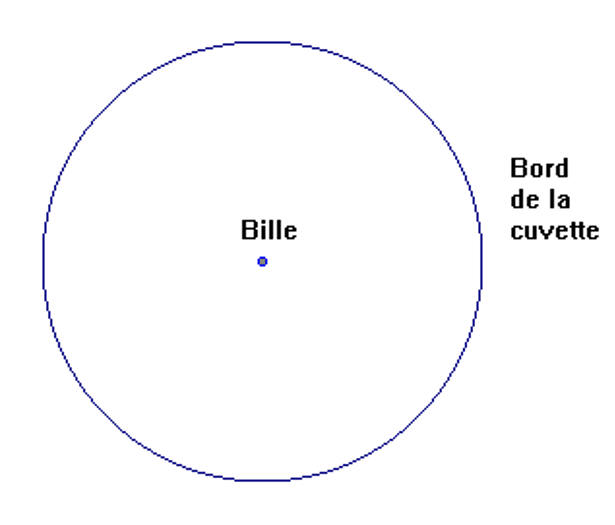
Qu’observe-t-on alors à la surface de l’eau ?
comment
se fait la propagation ? 4)-
L’onde touche le bord de la cuvette à l’instant
t = 0,10 s. En déduire la
célérité des ondes à la surface de l’eau. 5)-
Comment serait modifiée la célérité : - Si la goutte tombait à
- Si on remplaçait de l’eau par de
l’huile (de masse volumique plus faible) ? 6)-
Un bouchon de diamètre Son centre st situé à À quelle date se met-il en mouvement ? Quelle énergie peut-il récupérer au maximum ? |
|
Une petite bille tombe dans une cuvette cylindrique remplied’eau de
rayon
La bille est initialement à
On néglige les frottements de l’air. L’origine des temps est prise à l’instant du contact avec l’eau.
Le niveau de référence pour l’énergie potentielle
est la surface de
l’eau.
Le rayon de la bille est de
ρ = 2,0 x
10 3 kg . m – 3.
On prend : g = 9,8 N / kg. Le volume d’une sphère est :
-
1)-
En utilisant le cours de première
S, calculer la vitesse de la bille à l’instant où elle touche l’eau. - vitesse de la bille
à l’instant où elle touche l’eau. - La bille est
en chute libre. - On peut
utiliser la loi de la chute libre : - 2)- Au moment de l’impact, la bille perd la moitié de son énergie. De quel type d’énergie s’agit-il ?
Que
devient-elle ? - Au contact
de l’eau, la bille perd la moitié de son énergie cinétique.
- Une partie de cette énergie est transférée à l’eau (elle crée une perturbation à la surface de l’eau, elle permet de créer une onde. 3)-
Qu’observe-t-on alors à la surface de l’eau ?
comment
se fait la propagation ? - On observe
la propagation d’une onde mécanique
transversale progressive. - Une ride
circulaire se propage. -
La
propagation se fait de proche en proche. 4)- L’onde touche le bord de la cuvette à l’instant t = 0,10 s. En déduire la
célérité des ondes à la surface de l’eau. - Célérité de
l’onde : le rayon de la bille RB
= - En conséquence,
RB
<< RC.
- On peut
faire l’approximation suivante : - Pour parcourir
les - 5)-
Comment serait modifiée la célérité : - Si la goutte tombait à
- Si on remplaçait de l’eau par de
l’huile (de masse volumique plus faible) ? - La célérité
de l’onde ne dépend pas de la hauteur de chute de la bille. - Mais
l’amplitude de l’onde dépend de la hauteur de chute de la bille. -
Si l’on
remplace, l’eau par de l’huile, l’inertie de l’huile est plus faible que
celle de l’eau. - la célérité de
l’onde est plus grande dans l’huile que dans l’eau. 6)-
Un bouchon de diamètre À quelle date se met-il en mouvement ? Quelle énergie peut-il récupérer au maximum ? - Date de mise
en mouvement. - On connaît :
d = - Or :
- Énergie que
peut récupérer le bouchon : - Le bouchon a un
diamètre d = - L ‘énergie
initiale se répartie sur un cercle de périmètre
P =2.π.R. - Valeur de
l’énergie cinétique initiale : - - Valeur de
l’énergie initiale : - - énergie récupérée par un
bouchon de -
|