![]()
Le photon
Cours
Exercices
|
|
Le photon |
|
|
|
|
|
I- Manifestation du caractère corpusculaire de la lumière. |
|
La lumière : un flux de photons |
|
QCM r
|
I-
Manifestation du caractère corpusculaire de la
lumière.
-
Expérience de Hertz
(1887) :
►
Expérience avec
l’électroscope :
-
On charge négativement
un électroscope sur lequel on a posé une lame de zinc (Zn)
décapée et amalgamée avec du mercure (Hg).

-
On éclaire la lame de
zinc avec une lampe U.V.
-
On remarque que
l’électroscope se décharge rapidement.
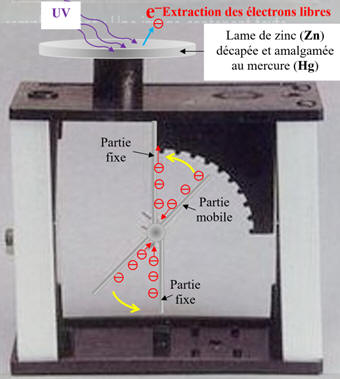
-
La lame de zinc, au
départ, est chargé négativement.
-
Elle possède un excès
d’électrons.
-
Si elle se décharge,
c’est que des électrons ont été arrachés au métal
-
C’est l’effet
photoélectrique.
-
L’énergie nécessaire à
l’extraction des électrons est fournie par la lampe
UV.
2)- Interprétation (EINSTEIN 1905).
-
Un faisceau lumineux
peut être considéré comme constitué de particules : les photons.
-
Chaque photon
transporte un quantum d’énergie :
-
E
= h
. υ
-
A. EINSTEIN explique
que l’énergie du photon sert en partie à arracher l’électron de l’atome, le
reste étant emporté par l’électron sous forme d’énergie cinétique.
- Ce résultat sera démontré expérimentalement par le physicien américain R. MILLIKAN (1868–1953) onze ans plus tard.
- La communauté scientifique mettra quelques années de plus
à accepter la notion d’aspect particulaire de la lumière.
-
En
1921, A. EINSTEIN obtiendra le prix Nobel de physique pour cette découverte.
-
En 1926, Gilbert
NEWTON nomme « photons » les particules de lumière porteuses de ces quanta
d’énergie.
-
Schéma :
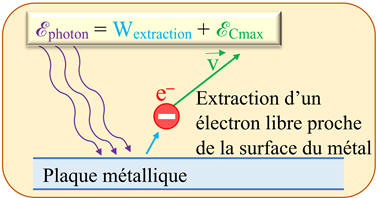
-
L’électron est arraché
au métal si l’énergie du photon incident est supérieure à l’énergie d’extraction
de l’électron du cristal.
-
Deux théories sont
nécessaires pour expliquer l’ensemble des phénomènes lumineux.
-
La
théorie
ondulatoire de la lumière pour interpréter les
phénomènes d’interférences et de diffraction ;
-
La
théorie
corpusculaire pour expliquer :
-
L’effet
photoélectrique
-
Les spectres
lumineux ;
-
L’effet Compton ;
-
Le rayonnement du
corps noir.
►
Exemple :
-
Quand on chauffe un
morceau de fer , il apparaît :
-
Rouge, orange, blanc
(vers 3000 °C), bleu pâle, puis sombre au-delà 6000 °C.
-
Le métal émet une
partie de l’énergie sous forme d‘un rayonnement électromagnétique.
-
Sa composition
spectrale dépend s de sa température.
-
La composition du
rayonnement émis par un corps noir est complétement indépendante de sa nature.
-
Elle ne dépend que de
sa température.
-
Aucune théorie
ondulatoire ne peut rendre compte de cette loi.
-
Loi de
Stefan-Boltzmann :
-
Puissance surfacique
émise par un corps noir :
-
p =
σ . T4
-
Constante
de Stefan-Boltzmann :
-
σ =
5,67 ×10–8 W . m–2 . K–4
-
T :
Température du corps noir en kelvin (K ).
Conversion de température :
T (K) = θ (° C) +
273. |
||||
|
|
-
Alors qu’une théorie
unique semble plus satisfaisante pour l’esprit, on se trouve dans l’obligation
de conserver ce double aspect (onde-corpuscule).
-
Pour lier les deux
aspects, le physicien français, Louis de Broglie a proposé en 1924, la mécanique
ondulatoire.
-
A tout
particule est associée une onde
ψ :
|
Particule |
|
|
m |
Masse en
kilogramme (kg) |
|
v |
Vitesse en mètre par seconde (m . s–1) |
|
h |
Constante de
Planck : h = 6,626 × 10–34 J . s |
-
Les unités :
-
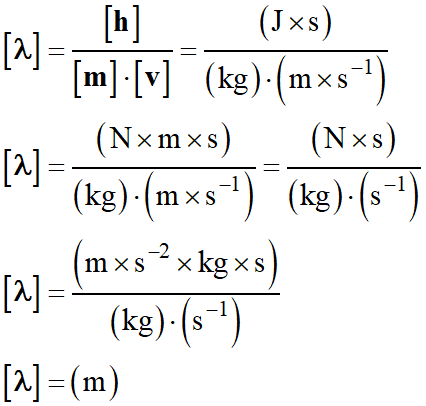
-
La
longueur d’onde λ
est bien homogène à une distance.
-
La lumière est
composée de particules appelées : photons.
-
Le photon est une
particule :
-
Non chargée ;
-
De masse nulle ;
-
Se
déplaçant à la vitesse
c0 =
3,00 × 108 m . s–1
dans le vide.
-
Tous
les photons d’une lumière monochromatique de fréquence
υ
transportent le même quantum d’énergie :
-
E
= h .
υ
-
La
grandeur h
est une constante Universelle :
-
h
= 6,626 × 10–34 J . s
-
L’électronvolt (eV)
est une unité adaptée pour donner l’énergie d’un photon. :
-
1 eV =
1,602 × 10–19 J
-
Énergie
E
du photon et sa longueur d’onde
λ :
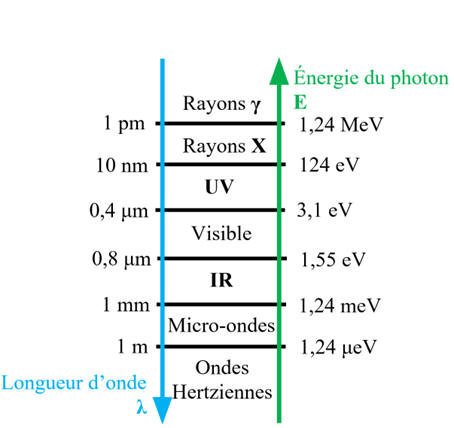
3)- Puissance énergétique d’une source lumineuse.
-
Elle dépend :
-
Du nombre N de photons
émis par seconde par la source ;
-
De l’énergie
transportée par chaque photon (E
= h .
υ).
-
Pour une source
monochromatique :
-
P
= N
. h .
υ
|
Puissance
énergétique |
P
= N . h . υ |
|
P |
Puissance
énergétique en watt (W) |
|
N |
Nombre de
photons émis par seconde (s–1) |
|
υ |
Fréquence
de la radiation monochromatique (Hz ou s–1) |
|
h |
Constante
de Planck : h = 6,626 × 10–34 J . s |
►
Énergie d’extraction :
-
L’énergie nécessaire à l’extraction d’un électron
e–
du sodium Na
vaut 2,3 eV.
-
Quelle
longueur d’onde maximale une lumière incidente peut-elle avoir pour produire
l’effet photoélectrique avec le sodium
Na ?
-
Situer la longueur
d’onde dans le spectre.
►
Réponses :
-
Remarque :
-
Si la longueur d’onde
d’une radiation augmente, l’énergie du photon associé à cette radiation diminue.
-
Relation
fondamentale :
-
![]()
-
E
= h .
υ
et ![]()
-
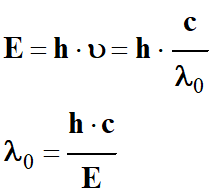
-
Application
numérique :
-
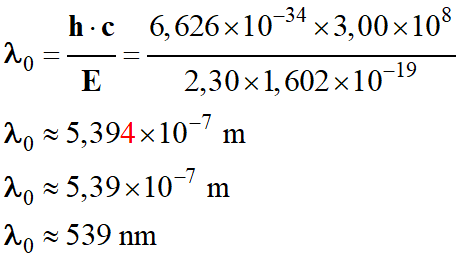
-
Pour extraire un
électron, la longueur d’onde de la radiation :
-
λ0
≤ 539 nm
-
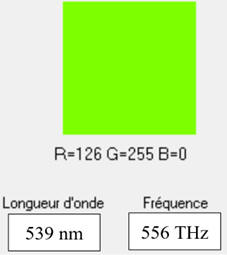
cette radiation
appartient au domaine du visible.
-
Couleur : jaune-vert.
►
Énergie de liaison :
-
L’énergie de liaison
covalente d’une molécule de dichlore est
-
ℰℓ
= 4,19 × 10–19 J
-
Cette
molécule peut être décomposée en deux atomes de chlore
Cℓ
sous l’action d’un photon :
|
|
h
. υ |
|
|
Cℓ2 |
→ |
Cℓ. +
Cℓ. |
|
|
|
|
-
Calculer la valeur de la longueur d’onde
λ
d’un photon capable de rompre cette liaison.
-
Quelle source de
rayonnement utilise-t-on en chimie pour obtenir ce résultat ?
►
Réponses :
-
Valeur
de la longueur d’onde
λ d’un photon capable de rompre la
liaison Cℓ
– Cℓ.
-
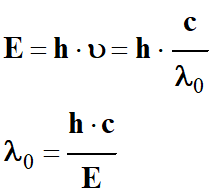
-
Application
numérique :
- 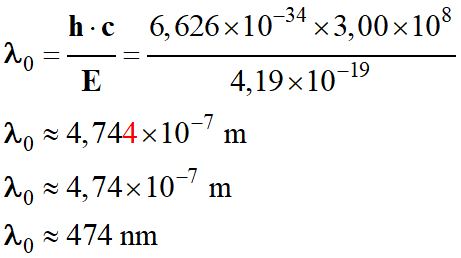
-
Source de rayonnement
utilisée en chimie pour obtenir ce résultat :
-
Lumière
riche en UV ;
-
Lumière émise par la
combustion d’un ruban de magnésium ;
-
Lumière solaire ;
-
Lampe halogène, lampe
à quartz.
►
L’effet Compton : On
parle aussi de diffusion Compton :
-
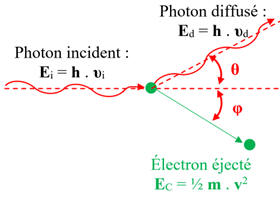
Ce
phénomène se manifeste lorsqu’un photon
X
incident entre en collision avec un électron libre d’un métal.
-
Au cours de ce
phénomène, l'électron est éjecté de l'atome, qui est alors ionisé et un photon
est diffusé.
-
En 1923, Arthur
Compton observe l'allongement de la longueur d'onde du photon X lors de cette
diffusion.
-
λd
> λi
ou υd
< υi
►
Application
-
Lors de
l’expérience d’effet Compton, on considère le choc d’un photon
X
incident d’énergie
Ei = 1,0 × 105 eV
sur un électron au repos.
-
Cet
électron acquiert une énergie cinétique de
EC
= 3,0 × 103 eV et un
photon diffusé.
-
En
utilisant le principe de conservation d’énergie, déduire la valeur de la
fréquence υd
et la longueur d’onde
λd du
photon diffusé.
-
Quel
est l’écart Δλ
entre la longueur d’onde du photon incident
λi
et du photon diffusé λd?
►
Réponses :
-
Schémas :
|
|
|
►
Réponses :
-
Fréquence du photon
incident :
-
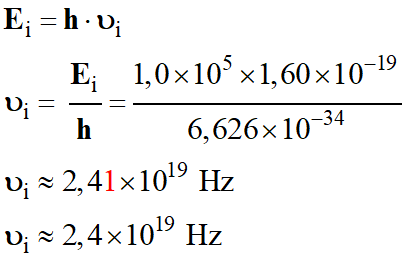
-
Fréquence du photon
incident :
-
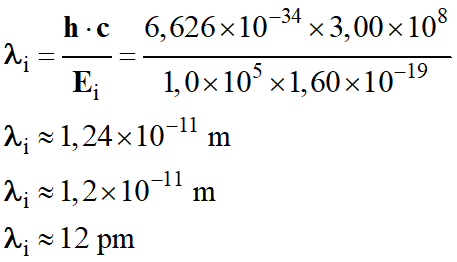
-
Conservation de
l’énergie :
-
Le
système S
= {photon, électron}
-
Avant :
-
L’électron est au
repos : son énergie cinétique est nulle.
-
Le
photon X
possède l’énergie
Ei.
-
Après :
-
L’électron possède de l’énergie cinétique
EC
= ½ m
. v2
-
Le photon diffusé
transporte de l’énergie.
-
On note
Ed
l’énergie du photon diffusé :
-
Ei =
EC
+ Ed
-
Ed
= h
. υd
= Ei –
EC
-
Fréquence du photon
diffusé
- 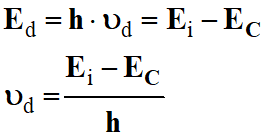
-
Application
numérique :
-
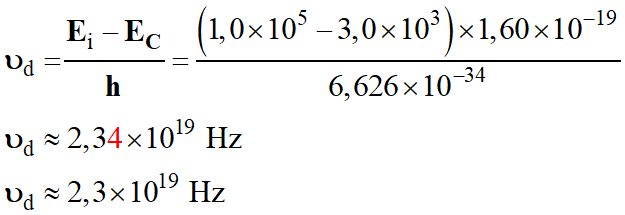
-
Longueur d’onde du
photon diffusé :
- 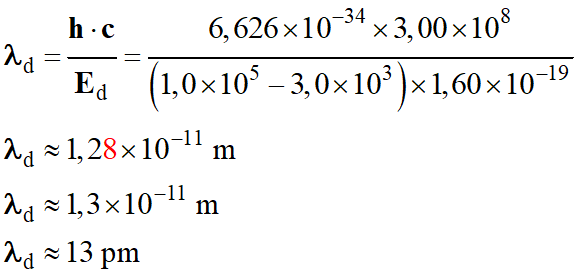
-
Remarque :
-
υi
> υd
=> λi
< λd
-
Écart entre les
longueurs d’onde :
-
Δλ
= λd
– λi
-
Δλ
≈ 13 pm – 12 pm
-
Δλ
≈ 1,0 pm
-
Si on garde les
calculs intermédiaires dans la mémoire de la calculatrice :
-
Δλ
= λd
– λi
-
Δλ
≈ 0,40 pm
|
|