![]()
|
|
|
|
|
|
|
|
QCM r
|
2)- Exercice : Charge d’un condensateur à intensité constante
|
Charge d’un condensateur à intensité constante : Un condensateur (MN ), de capacité 3,0 mF, a été chargé par un courant d’intensité constante I0 = 2,0 μA arrivant sur l’armature N
pendant 2 minutes 30 secondes. 1.
Quelles sont les quantités d’électricité
portées par chacune des armatures du condensateur ? 2.
Quel est la valeur de la tension uMN
aux bornes du condensateur ainsi chargé ? |
|
Charge d’un condensateur à intensité constante : Un condensateur (MN ), Capacité du condensateur C = 3,0 mF,
Générateur de courant : Intensité constante : I0
= 2,0 μA arrivant sur l’armature N Durée : Δt = 2 minutes 30 secondes = 150 s Représentation d’un condensateur :
-
Représentation : convention
récepteur.
-
On écrit :
Schéma du montage :
1.
Quantités d’électricité portées par chacune
des armatures du condensateur :
-
L’armature N porte la charge
électrique qN positive.
-
L’armature M porte la charge
électrique qM négative.
-
Relation :
qM = – qN
-
D’autre part :
-
qN =
I0 × Δt
-
qN = 2,0 × 10–6
× 150
-
qN ≈ 3,0 × 10–4
C
-
En conséquence :
-
qM ≈ – 3,0 × 10–4
C 2.
Valeur de la tension uMN
aux bornes du condensateur ainsi chargé :
-
Par définition :
-
-
Or :
uMN = –
uNM
-
|
||||||||
3)- Exercice : Charge d’un condensateur à tension constante.
|
Charge d’un condensateur à tension constante : Au cours de la charge, à tension constante, d’un condensateur de capacité C à travers un conducteur ohmique de résistance R, on a relevé ta tension aux bornes du condensateur en fonction du temps. On a obtenu le graphique représenté sur le schéma ci-dessous. Le générateur de charge est un générateur idéal de tension de
f.é.m. E. 1.
Commenter le graphique obtenu. 2.
Quelle est la tension aux bornes du
condensateur en fin de charge. 3.
: a.
Tracer la tangente à la courbe à l’instant
t = 0 s. b. À partir du point d’intersection de cette tangente avec l’asymptote horizontale de la courbe de charge, en
déduire la constante de temps τ du circuit. c. Une autre méthode de calcul de τ consiste à déterminer la durée pour laquelle le condensateur possède 63 % de sa charge maximale. Comparer les valeurs obtenues par
les deux méthodes. 4.
Quelle est la valeur de la capacité C
du condensateur si R = 2200 Ω ? |
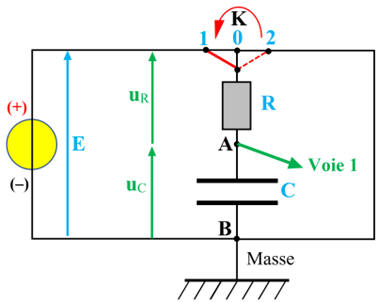
Charge d’un condensateur à tension constante :
-
Schéma du montage :
-
E = ? ,
R = 2200 Ω , C
= ?
-
Initialement, le condensateur est
déchargé et l’interrupteur est en position 2 : uC
= 0 V
-
À la date t = 0 s, on bascule
l’interrupteur sur la position 1.
-
Graphique obtenu : 1.
Commentaires sur le graphique obtenu.
-
On observe la charge du condensateur
à tension constante au cours du temps.
-
Le phénomène est transitoire :
-
Il existe un régime transitoire : le
condensateur se charge
-
Il existe un régime permanent : le
condensateur est chargé.
-
La tension augmente au cours du temps
et tend asymptotiquement vers une valeur égale à la tension
d’alimentation :
-
Lorsque le condensateur est chargé,
l’intensité est nulle dans le circuit :
-
uC =
E ≈ 5,0 V
-
Loi des mailles (additivité des
tensions) :
-
E =
uR + uC
-
E =
R . i + uC
-
Lorsque le condensateur est chargé :
i = 0
-
E =
uC 2.
Tension aux bornes du condensateur en fin de
charge.
-
Lorsque le condensateur est chargé,
l’intensité est nulle dans le circuit :
-
uC =
E ≈ 5,0 V
-
Loi des mailles (additivité des
tensions) :
-
E =
uR + uC
-
E =
R . i + uC
-
Lorsque le condensateur est chargé :
i = 0
-
E =
uC
-
Exploitation graphique : 3.
: a.
Tangente à la courbe à l’instant t =
0 s.
-
Graphe : b.
Constante de temps τ du circuit.
-
À la date t = 0 s, on bascule
l’interrupteur sur la position 1.
-
Recherche de l’expression littérale
de :
-
Avec :
-
Loi des mailles :
-
E = uR +
uC
-
-
Au temps t = 0 s :
-
-
-
Pour déterminer graphiquement la
valeur de τ, on trace la tangente à l’origine à la courbe
uC = f (t).
-
L’abscisse du point
M d’intersection de la tangente avec l’asymptote horizontale donne
la valeur de la constante de temps
τ.
-
À partir du graphe : τ ≈ 10 ms c.
Autre méthode de calcul de τ :
-
On l’appelle la constante de temps,
notée τ :
-
τ =
R .
C
-
Le temps caractéristique
τ (ou constante de temps)
de la charge ou de la décharge d’un dipôle
RC série est défini par
la relation suivante :
τ =
R . C
τ
Constante de temps ou temps caractéristique en seconde
(s)
R
Résistance du conducteur ohmique en ohm (Ω)
C
Capacité du condensateur en farad (F,
μF,
nF ou pF)
►
Remarque :
-
Si on charge le condensateur pendant
la durée Δt = τ , la tension aux bornes du condensateur est
égale à 63 % de sa tension maximale Umax
= E.
-
-
Si Δt = 5 τ , alors :
-
-
Tension aux bornes du condensateur au bout de la durée
τ.
-
-
Graphe :
-
Comparaison des deux méthodes :
-
On trouve la même valeur pour
τ.
-
Il vaut mieux utiliser les deux
méthodes car la tangente à l’origine est parfois délicate à tracer. 4.
Valeur de la capacité C du
condensateur si R = 2200 Ω ?
-
Le temps caractéristique
τ (ou constante de temps) de la charge ou de la décharge d’un dipôle
RC série est défini par
la relation suivante :
τ =
R . C
τ
Constante de temps ou temps caractéristique en seconde
(s)
R
Résistance du conducteur ohmique en ohm (Ω)
C
Capacité du condensateur en farad (F, μF, nF ou pF)
-
►
Additif :
►
Établissement de l’équation
différentielle vérifiée par la tension uC :
-
Loi d’Ohm aux bornes du conducteur
ohmique : uR =
R .
i
-
Relations pour le condensateur :
uC
Tension aux bornes du condensateur en volt (V)
qA
Charge de l’armature A du condensateur en coulomb
(C)
i
Intensité du courant en ampère (A)
C
Capacité du condensateur en farad (F, μF, nF ou pF)
-
Loi des mailles (additivité des
tensions) :
-
E =
uR + uC
-
E = R . i + uC
avec
-
On en déduit l’équation
différentielle vérifiée par la tension
uC lors de la charge :
-
►
Solution de l’équation
différentielle vérifiée par la tension uC lors de la
charge :
-
Les solutions d’une équation
différentielle y’ =
a . y + b avec
a ≠ 0, sont de la forme :
-
-
La constante K est liée aux
conditions initiales.
-
Les constantes a et
b sont liées aux
caractéristiques du circuit.
-
En utilisant la formulation
précédente :
-
-
Avec comme solution :
-
-
On en déduit que :
-
-
Recherche de l’expression de
K :
-
Au temps
t = 0 s,
uC (0) = 0 le
condensateur est déchargé :
-
-
Solution de l’équation
différentielle :
-
-
Comme :
τ = R .
C
-
-
Au bout de la durée τ la tension aux bornes du
condensateur est la suivante :
-
-
Or :
e ≈ 2,718
-
-
Au bout de la durée τ, la tension aux bornes du condensateur est :

![]()



![]()
![]() .
.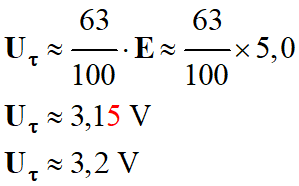

![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
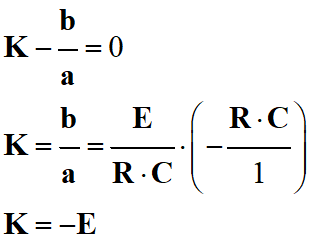

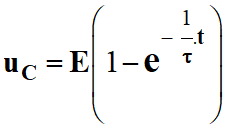
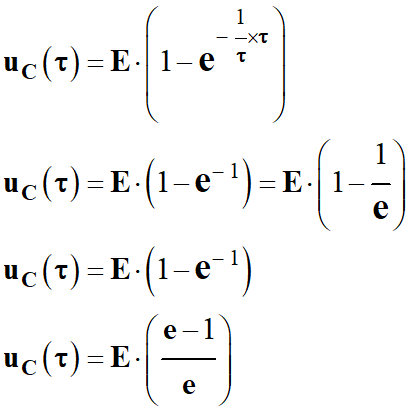

![]()
![]()
4)- Exercice : Charge et intensité algébrique.
|
Charge et intensité algébrique : Le condensateur de capacité C est chargé à travers une résistance R à l’aide d’un générateur idéal de tension de
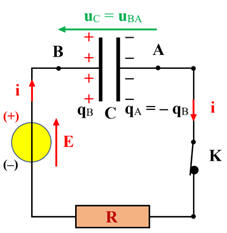
f.é.m E. Schéma du circuit :
1.
Donner le signe : a.
De qB. b.
De 2.
: a.
Donner la relation entre i et
b.
La charge qA
augmente-t-elle ou diminue-t-elle ? c.
En déduire le sens du courant. |
Charge et intensité algébrique : Schéma du circuit : 1.
: a.
Signe de qB.
-
D’après l’orientation donnée à la
source idéale de tension, le courant arrive à la borne
B du condensateur.
-
La charge portée par l’armature
B du condensateur est
positive : qB
> 0 b.
Signe de
-
Au cours de la charge du condensateur
sous tension constante, la charge portée par l’armature
B augmente :
-
2.
: a.
Relation entre i et
-
Schéma du circuit :
-
Dans le cas présent :
-
-
L’intensité du courant est la
dérivée, par rapport au temps, de la charge électrique qB .
-
-
Comme :
qA = – qB
-
b.
Évolution de la charge qA
cours du temps.
-
La charge
qA portée par
l’armature A est
négative : qA
< 0
-
Elle diminue au cours du temps, mais
augmente en valeur absolue. c.
Sens du courant dans le circuit.
-
Le courant circule dans le sens
positif choisi.

![]()
![]()
![]() .
.
![]()
![]()
![]()
![]()
5)- Exercice : Énergie stockée dans un condensateur.
|
Énergie stockée dans un condensateur : Un condensateur de capacité C = 1,0 F ne peut supporter
entre ces bornes une tension supérieure à 5,0 V. 1.
Quelle est la valeur maximale de l’énergie
qu’il est susceptible de stocker ? 2.
Quelle est alors la quantité d’électricité
portée par chacune des armatures ? 3. Le condensateur chargé sous 5,0 V est ensuite déchargé dans une résistance R. Quelle doit-être la valeur de
celle-ci, l’intensité maximale du courant ne devant pas dépasser 2,0
A ? |
|
Énergie stockée dans un condensateur : Un condensateur de capacité C = 1,0 F ne peut supporter
entre ces bornes une tension supérieure à 5,0 V. Schéma du circuit :
1.
Valeur maximale de l’énergie qu’il est
susceptible de stocker :
-
On charge le condensateur avec une
source idéale de tension de force électromotrice :
-
E = 5,0 V
-
Relations importantes :
-
La charge qA de
l’armature A d’un condensateur est proportionnelle, à chaque
instant, à la tension uAB = uC
entre ses bornes :
-
L’intensité du courant est la
dérivée, par rapport au temps, de la charge électrique qA :
-
L'énergie stockée par le condensateur
est de l'énergie potentielle électrostatique :
-
-
Application numérique :
-
2.
Valeur de la quantité d’électricité portée
par chacune des armatures :
-
Schéma :
-
Quantité d’électricité
qA portée par l’armature
A :
-
qA =
C .
uC
-
qA = 1,0 × 5,0
-
qA ≈ 5,0 C
-
Quantité d’électricité
qB portée par l’armature
B :
-
qB = –
qA
-
qB ≈ – 5,0 C 3.
Valeur de la résistance R :
-
Le condensateur chargé sous 5,0 V :
-
Décharge dans une résistance R :
-
Intensité maximale du courant :
Imax ≤ 2,0 A
-
Schéma du montage :
-
Lorsque le condensateur est chargé,
on bascule l’interrupteur sur la position 2 pour le décharger.
-
Loi des mailles (additivité des
tensions) :
-
uR + uC
= 0
-
R . i + uC
= 0 avec
-
On en déduit l’équation
différentielle vérifiée par la tension uC lors de
la décharge :
-
►
Solution de l’équation différentielle
vérifiée par la tension uC lors de la décharge :
-
Les solutions d’une équation
différentielle y’ = a . y + b avec a
≠ 0, sont de la forme :
-
-
La constante K est liée aux
conditions initiales.
-
Les constantes a et b
sont liées aux caractéristiques du circuit.
-
En utilisant la formulation
précédente :
-
-
Avec comme solution :
-
-
On en déduit que :
-
-
Recherche de l’expression de K :
-
Au temps t = 0 s, uC
(0) = E : le
condensateur est chargé :
-
K = E
-
Solution de l’équation
différentielle :
-
-
Le produit R .
C représente le temps
caractéristique du dipôle RC série.
-
Il a la dimension d’un temps.
►
Allure de la courbe :
-
Or :
-
-
L’intensité du courant est négative.
-
Le courant circule dans le sens
inverse du sens positif choisi.
-
L’intensité est maximale, en valeur
absolue au temps t = 0 s
-
-
Car
E et
R sont des grandeurs
positives.
-
On peut en déduire la valeur de la
résistance R lors de la décharge :
-
-
La valeur de la résistance R du circuit doit être supérieure ou égale à 2,5 Ω. |
||||||||||||||||||||||||
6)- Exercice : Charge et décharge d’un condensateur : visualisation à l’oscilloscope.
|
Charge et décharge d’un condensateur : visualisation à
l’oscilloscope : Afin d’étudier la charge et la décharge d’un condensateur, on
réalise un circuit comportant en série :
-
Un G.B.F délivrant une tension en
créneaux ;
-
Un conducteur ohmique de résistance
R = 200 Ω.
-
Un condensateur de capacité
C. On obtient les oscillogrammes ci-dessous :
1.
: a.
Quelle est la courbe qui représente :
-
La tension uMN aux
bornes du conducteur ohmique ?
-
La tension uNP aux
bornes du condensateur ? b.
En déduire celle qui permet de connaître les
variations de l’intensité du courant en fonction du temps. c.
À quoi correspondent les deux parties de
chaque courbe ? 2.
Déterminer grâce aux oscillogrammes, les
grandeurs suivantes : a.
La tension maximale aux bornes du
condensateur ; b.
La tension maximale aux bornes du conducteur
ohmique ; c.
L’intensité maximale du courant de charge ; d.
La valeur approximative de la constante de
temps τ ; e.
La valeur approximative de la capacité C. |
|
Charge et décharge d’un condensateur : Visualisation à
l’oscilloscope :
-
Un G.B.F délivrant une tension en
créneaux ;
-
Un conducteur ohmique de résistance
R = 200 Ω.
-
Un condensateur de capacité
C.
-
Montage :
1.
: a.
Courbe qui représente :
-
La courbe 1 représente la tension uMN aux bornes du conducteur ohmique :
-
Avec l’orientation choisie : uMN
= R .
i
-
La courbe 2 représente la tension
uPN
-
Avec l’orientation choisie : uPN
= – uPN = –
uC - Pour visualiser la tension aux bornes du condensateur, on appuie sur la touche –
B (ou
– CH2) de la voie
B ou 2 de l’oscilloscope. b.
Courbe qui permet de connaître les
variations de l’intensité du courant en fonction du temps.
-
Courbe 1 :
-
Avec l’orientation choisie au temps
t :
-
uR =
uMN =
R .
i
-
En conséquence :
-
La courbe 1 permet de connaître les
variations de l’intensité du courant
i ceci à une constante
près. c.
Étude des deux parties de chaque courbe :
-
Première partie :
-
Charge du condensateur : l’intensité
diminue et s’annule lorsque le condensateur est chargé. - Décharge du condensateur : l’intensité du courant change de sens et elle s’annule lorsque le
condensateur est déchargé.
-
Remarque :
-
Loi des mailles :
-
uMP =
uMN +
uNP
-
uMP =
R .
i + uC - Le G.B.F délivre une tension E = 4 ,00 V pendant une durée de 10 ms, puis une tension nulle pendant une durée de 10 ms.
-
Lorsque le condensateur est chargé,
l’intensité du courant dans le circuit est nulle :
-
uMP =
uC
-
Schéma :
-
E ≈ 2 div × 2,0 V/div
-
E ≈ 4,0 V 2.
Détermination grâce aux oscillogrammes, des
grandeurs suivantes : a.
Tension maximale aux bornes du condensateur
-
UCmax = 4,0 V b.
Tension maximale aux bornes du conducteur
ohmique
-
URmax = 4,0 V c.
Intensité maximale du courant de charge
-
On peut écrire, en valeur absolue :
-
Umax =
R .
Imax
-
d.
Valeur approximative de la constante de
temps τ
-
Graphe :
-
La durée de charge du condensateur :
-
Δt ≈ 2 div × 2,0 ms/div
-
Δt ≈ 4,0 ms
-
Un condensateur est chargée à plus 99
% au bout de la durée :
-
Δt ≈ 5
τ
-
On peut en déduire une valeur
approximative du temps caractéristique
τ.
-
e.
Valeur approximative de la capacité C
-
On utilisation la relation liant la
constante de temps τ aux
caractéristiques R et
C du circuit.
-
τ =
R . C
-
|
7)- Exercice : Étude de la réponse d’un dipôle (R, C) à une tension en créneau.
|
Étude de la réponse d’un dipôle (R, C) à une
tension en créneau : On veut étudier en travaux pratiques, la réponse d’un dipôle (R,
C) à une tension en créneau. Les objectifs sont :
-
La visualisation de l’évolution de la
tension uC aux bornes du
condensateur ;
-
La visualisation de l’évolution de la
tension aux bornes du G.B.F. ;
-
L’étude de l’influence des divers
paramètres sur l’évolution de
uC en
fonction du temps. On dispose du matériel suivant :
-
Trois condensateurs : 1 F, 1 μF, 1
nF ;
-
Trois résistances : 102 Ω,
103 Ω, 104 Ω ;
-
Un
G.B.F. ;
-
Un oscilloscope bicourbe dont la base
de temps s’échelonne entre :
-
100 ms . div–1 et 0,2 μs .
div–1. 1.
Dans le cas de chacun des trois objectifs
cités plus haut, indiquer : a.
Le schéma du montage utilisé comprenant les
valeurs choisies pour R et C ; b.
Le protocole expérimental (le décrire
brièvement). 2. On a obtenu les deux oscillogrammes suivants pour des fréquences différentes de la tension en créneaux délivrée par le générateur pour un dipôle (R, C). La courbe Y1 correspond à la tension délivrée par le G.B.F. , la courbe
Y2 à la tension aux bornes du condensateur. a.
Reconnaître, sur l’un des oscillogrammes,
les portions de courbe correspondant à la charge ou à la décharge. b.
Expliquer l’évolution de la forme de la
réponse obtenus sur la courbe Y2. Données : R = 1 kΩ et C = 1 μF
|
|
Étude de la réponse d’un dipôle (R, C) à une
tension en créneau : 1.
Dans le cas de chacun des trois objectifs
cités plus haut, indiquer : a.
Schéma du montage utilisé comprenant les
valeurs choisies pour R et C :
-
Schéma :
-
Voie
Y1 : Tension
uMP : Tension
aux bornes du générateur (G.B.F.)
-
Voie
Y2 : Tension
uNP : Tension
aux bornes du condensateur (uC)
-
Réglages préliminaires de
l’oscilloscope :
-
Base de temps :
-
On observe une ligne lumineuse pour
chaque voir :
-
La voie 1 ou
Y1 : On déplace la ligne lumineuse vers le haut et au
milieu de cette partie.
-
La voie 2 ou
Y2 : On déplace la ligne lumineuse vers le bas et au
milieu de cette partie.
-
Sensibilité verticale :
-
Oscillogramme obtenu :
b.
Le protocole expérimental (le décrire
brièvement).
-
On règle l’oscilloscope afin
d’obtenir un oscillogramme exploitable :
-
On doit observer d’une à deux
périodes du signal donné par le
G.B.F.
-
Le temps caractéristique du circuit :
-
τ =
R .
C
-
Au bout de la durée
Δt = 5 τ, le condensateur
est chargé à plus de 99 %.
►
1ier cas :
-
Si
C = 1 F et
R = 100 Ω, alors
τ =
R . C = 100 s
-
Pour observer la charge ou la
décharge du condensateur :
-
Δt = 500 s,
-
On ne peut observer, ni la charge, ni
la décharge.
-
La sensibilité horizontale maximale
est : b = 0,2 s . div–1.
-
L’écran d’un oscilloscope fait 10 div
sur 8 div :
►
Deuxième cas :
►
3ième Cas :
2. On a obtenu les deux oscillogrammes suivants pour des fréquences différentes de la tension en créneaux délivrée par le générateur pour un dipôle (R, C). La courbe Y1 correspond à la tension délivrée par le G.B.F. , la courbe
Y2 à la tension aux bornes du condensateur.
-
Oscillogrammes : Données : R = 1 kΩ et C = 1 μF
a.
Les portions de courbe correspondant à la
charge ou à la décharge.
-
Oscillogrammes : b.
Évolution de la forme de la réponse obtenus
sur la courbe Y2.
-
Si
C = 1 μF et
R = 1 kΩ, alors
τ =
R . C = 1 ms
-
Pour observer la charge ou la
décharge du condensateur :
-
Δt ≥ 5 ms,
-
Pour
Δt ≥ 5
τ, le condensateur a le
temps de se charger et de se décharger complétement.
-
Pour Δt ≈
τ, le condensateur n’a
plus le temps de se charger et de se décharger. |
|
|