|
QCM N° 06 |
Circuit RC
Cours : 2018 Cours : 2002 Cours : 2000 |
|
|
|
Pour chaque question, indiquer la (ou les) bonne(s) réponse(s). |
|||||
|
|
Énoncé |
A |
B |
C |
R |
|
1 |
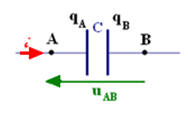
La tension uAB entre les bornes A et B d’un dipôle est : |
Égale à la différence de potentiel (VA – VB) entre ses deux points. |
Est représentée par une flèche tracé hors du circuit et orientée de B vers A. |
Est représentée par une flèche tracé hors du circuit et orientée de A vers B. |
AB |
|
2 |
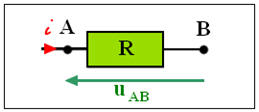
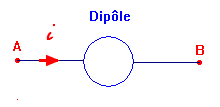
Soit un dipôle RC suivant :
La flèche représente la tension : |
uAB |
uBA |
uCB |
B |
|
3 |
On considère le dipôle ci-dessus. Dans le cas présent, on utilise : |
La convention générateur |
La convention récepteur |
La loi d’Ohm |
B |
|
4 |
On charge un condensateur, à courant constant, avec une intensité I = 50,0 mA pendant une durée Δt = 3,0 min. La charge Q du condensateur est alors : |
Q ≈ 150 C |
Q ≈ 9,0 x 103 C |
Q ≈ 9,0 C |
C |
|
5 |
Pour pouvoir écrire les lois physiques relatives aux différents dipôles : |
Il faut nécessairement orienter le circuit ou la branche de circuit dans lequel les dipôles se trouvent |
Il n’est pas nécessaire d’orienter le circuit ou la branche de circuit dans lequel les dipôles se trouvent |
Il suffit d’utiliser l’additivité des tensions |
A |
|
6 |
La loi d’Ohm, aux bornes du conducteur ohmique représenté sur le schéma ci-dessus, est donnée par la relation : |
uAB = – R . i |
uAB = R . I |
uAB = R . i |
C |
|
7 |
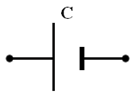
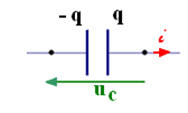
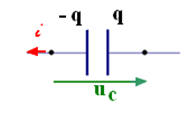
La représentation symbolique du condensateur est donnée par le schéma : |
|
|
|
A |
|
8 |
On considère le dipôle ci-dessus. On peut écrire la (les) relation(s) suivante(s) : |
|
|
|
BC |
|
9 |
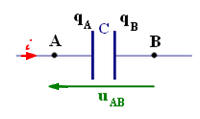
On considère le dipôle ci-dessus. En respectant les notations, on peut écrire la (les) relation(s) suivante(s) : |
|
|
|
C |
|
10 |
Soit un condensateur de capacité C. Dans le cas suivant, choisir la ou
les
relation(s) correcte(s) :
|
|
|
|
B |
|
11 |
Soit un condensateur de capacité C. Dans le cas suivant, choisir la ou
les
relation(s) correcte(s) :
|
|
|
|
AC |
|
12 |
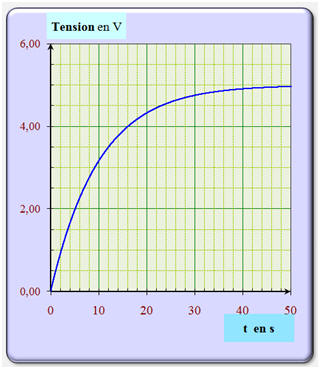
La courbe ci-dessus représente la charge du condensateur d’un dipôle RC soumis à un échelon de tension. La durée de cette charge dépend : |
Seulement de la valeur de la résistance R du conducteur ohmique |
Seulement de la valeur de la capacité C du condensateur |
De la valeur de la résistance R du conducteur ohmique et de la valeur de la capacité C du condensateur |
C |
|
|
|
|
|||
|
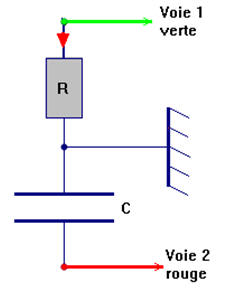
13 |
À l’aide d’un oscilloscope, on réalise les branchements (voir le schéma ci-dessus) sur un dipôle RC : On mesure l’intensité i du circuit, ceci à une constante près : |
Sur aucune des voies |
À la voie 1 de l’oscilloscope |
À la voie 2 de l ’oscilloscope |
B |
|
14 |
Un générateur qui délivre un échelon de tension donne : |
Une tension qui passe de façon instantané d’une valeur nulle à une valeur constante E |
Une tension périodique telle que uG = E sur la première demi-période et uG = – E sur la seconde demi-période |
Une tension triangulaire |
A |
|
15 |
Le condensateur est chargé à 63 % de sa charge maximale au bout de la durée : |
τ |
3 τ |
5 τ |
A |
|
16 |
Le condensateur est chargé à 99 % de sa charge maximale au bout de la durée : |
τ |
3 τ |
5 τ |
C |
|
17 |
La constante de temps τ, du circuit RC est donnée par la relation : |
|
|
|
C |
|
|
|
|
|||
|
18 |
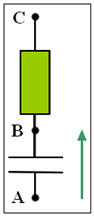
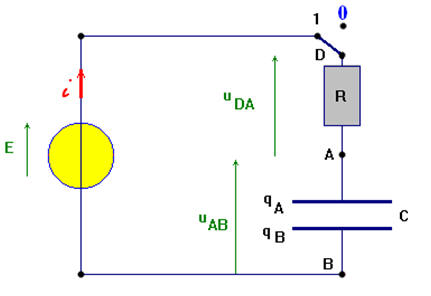
On étudie la charge d’un condensateur par un échelon de tension. Pour ce faire, on utilise le montage ci-dessus. À l’instant t =0 s, le condensateur étant déchargé, on bascule l’interrupteur sur la position 1. On obtient l’équation différentielle suivante :
|
C’est une équation différentielle linéaire du deuxième ordre avec second membre |
C’est une équation différentielle linéaire du premier ordre sans second membre |
C’est une équation différentielle linéaire du premier ordre avec second membre |
C |
|
19 |
L’équation différentielle suivante :
admet une solution de la forme : |
|
|
|
B |
|
20 |
Lors de la charge d’un condensateur par un échelon de tension, l’intensité i du courant dans le circuit : |
Est constante au cours du temps |
Est maximale à l’instant initial, puis diminue pour s’annuler lorsque le condensateur est chargé |
Est minimale à l’instant initial, puis augmente, passe par un maximum, puis diminue pour s’annuler lorsque le condensateur est chargé |
B |
|
21 |
La constante de temps d’un dipôle RC est : |
La durée nécessaire pour que le condensateur atteigne 63 % de sa charge maximale |
La durée nécessaire pour que le condensateur soit totalement chargé |
La durée nécessaire pour que le condensateur atteigne 37 % de sa charge maximale |
A |
|
22 |
On réalise un circuit RC en plaçant en série un condensateur de capacité C = 1000 μF et un conducteur ohmique de résistance R = 3,40 kΩ. Le dipôle RC, ainsi réalisé, a pour constante de temps : |
τ ≈ 3,40 s |
τ ≈ 3,40 × 103 s |
τ ≈ 3,40 × 10 – 3 s |
A |
|
|
|
||||
|
23 |
La courbe ci-dessus représente les variations de la tension aux bornes d’un condensateur en fonction du temps lors de sa charge. La constante de temps du circuit RC vaut : |
τ
≈ 100
ms |
τ ≈ 24
ms |
τ ≈ 12
ms |
B |
|
24 |
Un condensateur de capacité C chargé sous la tension u, emmagasine l’énergie : |
|
|
|
A |
Orientation d’un circuit et d’un dipôle.
- Pour pouvoir étudier le comportement électrique d’un dipôle électrique, il faut l’orienter le circuit ou la branche de circuit dans lequel il se trouve.
- On choisit dans le circuit série ou la branche d’un circuit un sens d’orientation arbitraire.
- Un courant électrique résulte d’un mouvement ordonné de porteurs de charge (les électrons dans un métal et les ions d’un un électrolyte).
- La mesure du débit de charges, exprimée en ampère (A), donne l’intensité du courant i qui est une grandeur algébrique.
- Si le courant circule dans le sens de la flèche alors i est positif, sinon, il est négatif.
- La tension uAB entre les bornes A et B d’un dipôle est égale à la différence de potentiel (VA – VB) entre ses deux points.
- La tension uAB , exprimée en volt (V), est représentée par une flèche tracé hors du circuit et orientée de B vers A.


- En convention récepteur, la flèche précisant l’orientation du dipôle est en sens contraire par rapport à la flèche utilisée pour représenter la tension u AB.
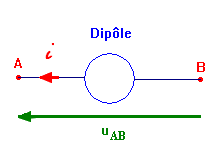
- En convention générateur, la flèche précisant l’orientation du dipôle est de même sens que la flèche utilisée pour représenter la tension u AB.
Courant et tension continus et courant et tension variables.
- Courant continu :
- En courant continu, l’intensité du courant est constante.
- On la note avec une lettre majuscule I.
- La quantité d’électricité Q qui traverse une portion de circuit pendant la durée Δt est donnée par la relation :
-
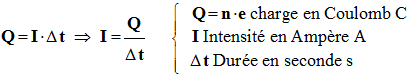
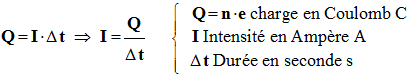
- De même une tension continue entre deux points A et B d’un circuit se note : UAB.
- Courants variables :
- Les courants et les tensions sont qualifiés de variables si leurs valeurs varient au cours du temps.
- On note ses grandeurs à l’aide de lettres minuscules : i pour l’intensité et uAB pour la tension entre deux points A et B d’un circuit.
- La loi d’additivité des tensions et la loi des nœuds sont vérifiées lorsque les circuits sont parcourus par des courants variables.
Le conducteur ohmique : Loi d’Ohm.
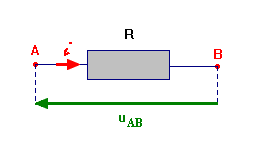
-
En courant variable, la Loi d’Ohm est toujours valable,
le fait d’orienter le circuit permet de pouvoir écrire la loi
d’Ohm :
- Dans le cas présent : uAB = R . i
- Remarque : uBA = – uAB = – R . i
- Un condensateur est formé de deux conducteurs métalliques appelés armatures, séparés par un isolant qui peut être de l'air ou un diélectrique.
- Le plus utilisé et le plus connu des condensateurs est le condensateur plan.
-
Symbole d’un condensateur :
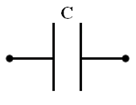
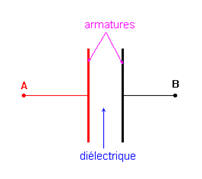
- Un condensateur est caractérisé par une grandeur physique appelée capacité, notée C.
- Elle s’exprime en farad (F). On utilise souvent le microfarad (μF) et le nanofarad (nF)
Loi d’Ohm pour un condensateur
- Représentation : convention récepteur :
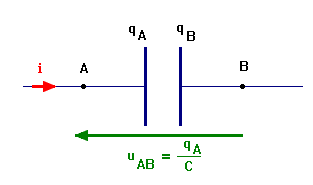
![]() ou
ou
![]()
- Un échelon de tension E est le passage instantané d'une tension de valeur nulle à une tension de valeur constante E.
- Représentation :

Constante de temps du circuit (R, C))
- La durée de charge du condensateur d'un dipôle (R, C) dépend de la résistance du conducteur ohmique et de la capacité du condensateur.
- La durée de charge du condensateur augmente avec la valeur du produit r.C.
- On appelle constante de temps du circuit (R, C), la valeur :τ = R.C.
- τ constante de temps : seconde s.
- R résistance du conducteur ohmique ohm Ω.
- C capacité du condensateur : farad F.
- Remarque : si on charge le condensateur pendant la durée Δt = τ , la charge Qτ portée par le condensateur est égale à 63 % de sa charge maximale Qmax.
-
On écrit :
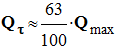
-
Si Δt = 5 τ, alors
:
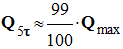 .
.
détermination
expérimentale de la constante de temps
t.
- Pour déterminer graphiquement la valeur de τ, on trace la tangente à l’origine à la courbe uAB = f (t) et l’asymptote horizontale à cette courbe.
- L’abscisse du point d’intersection de ces deux droites donne la valeur de la constante de temps τ.
-
On peut aussi utiliser le fait
qu’au bout de la durée τ,
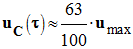
- uC (τ) ≈ 1,26 V
Charge d’un condensateur par un échelon de tension.
- Montage :
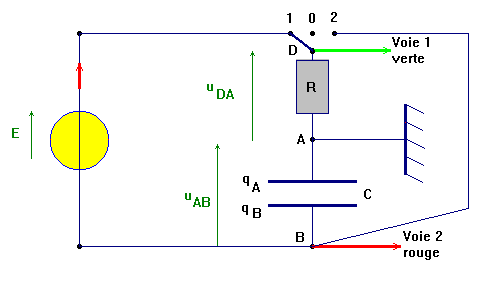
- Équation différentielle :
-
Loi d’ohm
aux bornes du conducteur ohmique :

-
Loi d’ohm
aux bornes du condensateur :
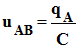
-
Relation entre l’intensité et la
tension uAB :
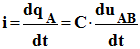
- Loi d’additivité des tensions :
-
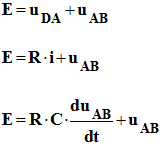
- Équation différentielle linéaire du premier ordre avec second membre.
- Solution :
-
On reconnaît une équation
différentielle du premier ordre avec deuxième membre qui admet
une solution du type :
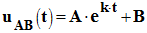
- où A, B et k sont des constantes.
- Expression des constantes dans le cas présent :
-
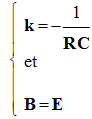
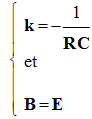
-
Solution :
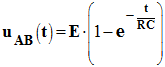
VVariation de l’intensité du courant dans le circuit au cours du temps
Énergie
emmagasinée dans un condensateur.
- Expression de l'énergie.
- Un condensateur de capacité C chargée sous la tension u emmagasine l’énergie :
-
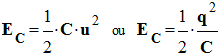
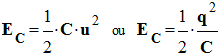
- EC : énergie en joule J
- C capacité en farad F
- u tension aux bornes du condensateur en volt V.
- C’est de l'énergie potentielle électrostatique.
|
|