![]()
|
|
|
|
|
|
|
|
QCM r
|
1)- Exercice 9 page 54 : Champs magnétiques créés par des aimants :
|
Champs magnétiques créés par des aimants : 1.
Comment peut-on détecter l’existence d’un
champ magnétique en un point de l’espace ? 2.
: a.
Représenter, en quelques points, au
voisinage d’un aimant droit, les vecteurs champ magnétique. b.
En déduite l’allure des lignes de champ
magnétique autour d’un aimant droit. |
|
Champs magnétiques créés par des aimants : 1.
Détection de l’existence d’un champ
magnétique en un point de l’espace :
-
Pour visualiser le spectre magnétique
d’un aimant, on peut utiliser
de la limaille de fer. En présence de l’aimant, les grains de
limaille de fer se comportent comme autant d’aiguilles aimantées qui s’orientent sous l’action du champ
magnétique.
-
Elles s’orientent et dessinent des
lignes, appelées lignes de champ. - L’ensemble des lignes de champ
donne le spectre magnétique.
-
On peut utiliser des aiguilles
aimantées.
-
L’aiguille aimantée subit une action
mécanique à distance de la part de l’aimant droit.
-
Par convention, on désigne par pôle
Nord l’extrémité d’une aiguille aimantée qui désigne le Nord géographique
et par pôle
Sud l’autre extrémité.
2.
: a.
Représentation du vecteur champ magnétique
au voisinage d’un aimant droit.
-
Aimant droit : b.
Allure des lignes de champ magnétique autour
d’un aimant droit.
-
On appelle ligne de champ, une courbe
de l’espace à laquelle le vecteur champ magnétique est tangent en
tout point.
-
La ligne de champ est orientée dans
le sens du champ.
-
Champ magnétique terrestre :
|
2)- Exercice 10 : Composition de champs :
|
Composition de champs : En un point de l’espace se superposent deux champs magnétiques
par deux aimants droits dont les directions sont orthogonales
(figure suivante). Leurs valeurs sont respectivement : B1 = 3,0 ×
10–3 T et B2 = 4,0 × 10–3 T. Schéma :
1.
Déterminer les noms des pôles des deux
aimants. 2.
Construire graphiquement le champ résultant
3.
Calculer la valeur de B et celle de 4.
Quelle est la position prise par une
aiguille aimantée (aimant témoin) placée au point M. |
|
Composition de champs : 1.
Les noms des pôles des deux aimants.
-
Représentation du champ magnétique :
-
En un point P de l’espace, le
champ magnétique est représenté par un vecteur :
-
Schéma :
2.
Construction graphique du champ résultant
-
Schéma :
3.
Valeur de B et valeur de
-
Valeur de
B :
-
-
Valeur de :
-
4.
Position prise par une aiguille aimantée
(aimant témoin) placée au point M.
-
Schéma :
|
3)- Exercice 13 : Champ créé par une bobine :
|
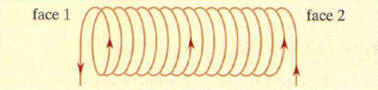
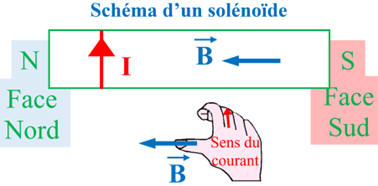
Champ créé par une bobine : Une bobine est parcourue par un courant comme l’indique le schéma
ci-dessous.
1.
Quelle est la direction du champ
Représenter les lignes de champ
en négligeant le champ magnétique terrestre. 2.
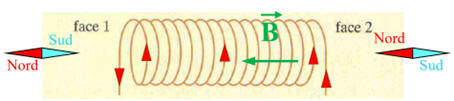
Indiquer comment s’orienterait l’aiguille
aimantée placée devant chaque face. 3.
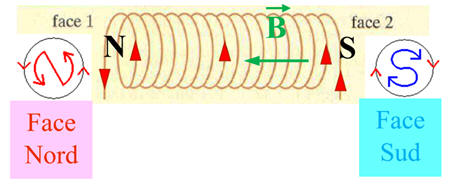
Donner le nom de chaque face. 4.
Donner la relation qui permet de calculer la
valeur B du champ magnétique à l’intérieur du solénoïde. |
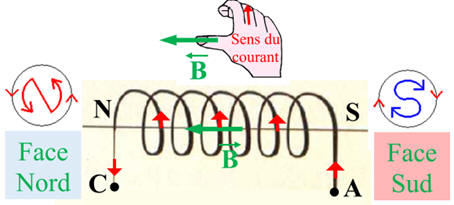
Champ créé par une bobine :
-
Schéma : 1.
Direction du champ
à l’intérieur de la bobine :
-
Schéma :
-
Lignes de champ :
-
On appelle ligne de champ, une courbe
de l’espace à laquelle le vecteur champ magnétique est tangent en
tout point.
-
La ligne de champ est orientée dans
le sens du champ. 2.
Orientation d’une aiguille aimantée placée
devant chaque face.
-
Schéma : 3.
Nom de chaque face.
-
Schéma : 4.
Relation qui permet de calculer la valeur
B du champ magnétique à l’intérieur du solénoïde.
Chap N° 14 Phénomène d’induction.
Exercices. Cas d’un solénoïde :
-
Caractéristiques du vecteur champ
magnétique
-
point d’application : le champ est uniforme
-
direction parallèle à l’axe du solénoïde
-
sens : il sort par le pôle Nord (règle de la main
droite)
-
valeur :
Avec
-
μ0 : perméabilité du vide :
-
μ0 = 4 π
-
N :
nombre total de spires
-
ℓ : longueur du solénoïde en mètre : m
-
-
I
intensité du courant en Ampère : A
-
B
valeur du champ magnétique en Tesla : T
-
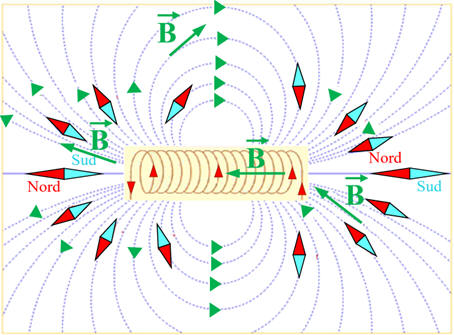
À l’extérieur le solénoïde se
comporte comme un aimant. - On peut considérer que la valeur du champ magnétique est
proportionnelle à l’intensité du courant
I.
-
B =
k .
I

![]() (à
l’intérieur du solénoïde).
(à
l’intérieur du solénoïde).
![]()
![]() ou B = μ0 . n . I
ou B = μ0 . n . I
![]() nombre de spires par mètre
nombre de spires par mètre![]()
|
Champ magnétique créé à l’intérieur d’une bobine : Une bobine de longueur ℓ = 50 cm, comportant
N = 1000 spires de
diamètre d = 4,0 cm, est parcourue par un courant d’intensité
I = 300 mA. 1. Peut-on considérer que le champ magnétique
au centre de la bobine est donné par la relation :
- B = 4 π × 10–7 ×
n × I ? 2. Quelles grandeurs représentent n et
I ? Indiquer leurs valeurs pour cette bobine dans le Système
International d’unités. 3. Calculer la valeur du champ magnétique à
l’intérieur du solénoïde. |
Champ magnétique créé à l’intérieur d’une bobine :
- Données :
- Longueur de la bobine : ℓ = 50
cm
- Nombre de spires :
N = 1000 spires - Diamètre d’une spire : d
= 4,0 cm.
- Intensité du courant :
I = 300 mA 1. Champ magnétique au centre de la bobine :
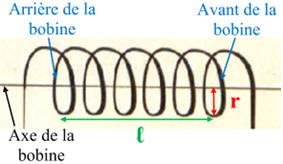
- Faces d’une bobine :
- Une bobine est constituée
d’un enroulement de fil conducteur, recouvert d’un vernis isolant,
sur un cylindre de
rayon
r.
- On désigne par
ℓ
la longueur de l’enroulement et par r le rayon d’une spire :
- Si
L
et petit devant
r,
la bobine est plate
- Si L est voisin de r la
bobine est appelée : solénoïde
- Si
L
est plus grand que 10
r,
le solénoïde est dit infini. Une bobine parcourue par un courant se comporte comme un aimant,
elle possède une face Nord et une face Sud.
- Dans le cas présent,
ℓ = 25
r - On est en présence d’un solénoïde infini.
- Le champ magnétique à l’intérieur
d’un solénoïde est pratiquement uniforme. - Les lignes de champ à l’intérieur du solénoïde sont des droites
parallèles.
- Cas d’un solénoïde :
- Caractéristiques du vecteur champ
magnétique (à l’intérieur du solénoïde).
-
Point d’application : le
champ est uniforme
-
Direction parallèle à l’axe
du solénoïde
-
Sens : il sort par le pôle
Nord (règle de la main droite)
-
Valeur :
Avec
-
μ0 :
perméabilité du vide :
-
μ0 =
4 π
x 10–
7 S.I (henry / mètre : H / m)
-
N :
nombre total de spires
-
ℓ :
longueur du solénoïde en mètre m
-
-
I
intensité du courant en ampère A
-
B
valeur du champ magnétique en tesla T
- Relation : B = 4 π × 10–7 × n × I 2. Les grandeurs n et I .
- Valeurs pour cette bobine dans le
Système International d’unités : -
-
- I intensité du courant en
ampère A
-
I = 300 mA = 0,300 A 3. Valeur du champ magnétique à l’intérieur du
solénoïde.
- B = 4 π × 10–7 ×
n × I - B ≈ 4 π × 10–7 ×
2,0 × 103
× 0,300
- B ≈ 7,5 × 10–4 T

![]()
![]() ou B = μ0 . n .
I
ou B = μ0 . n .
I
![]() nombre de spires par mètre
nombre de spires par mètre![]() :
nombre de spires par mètre.
:
nombre de spires par mètre.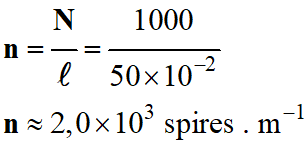
![]()
5)- Exercice 25 : Aiguille aimanté à l’intérieur d’une bobine :
|
Aiguille aimanté à l’intérieur d’une bobine : On dispose une aiguille aimantée à l’intérieur d’une bobine. En l’absence de courant, cette aiguille prend une direction
horizontale perpendiculaire à l’axe (x’x) de la
bobine. L’axe (x’x) est lui aussi horizontal. Schéma : 1.
Quelle est la direction du champ magnétique
terrestre ? 2.
On fait passer un courant d’intensité I.
L’aiguille aimantée dévie d’un angle α (schéma ci-dessus). a.
Déterminer le sens du courant dans la
bobine. b.
Calculer la valeur du champ créé par la
bobine et celle du champ résultant.
-
Données :
α = 30 ° ;
Bh = 2,0 × 10–5
T. 3.
Dessiner l’aiguille aimantée lorsque l’on
inverse le sens du courant. |
|
Aiguille aimanté à l’intérieur d’une bobine :
1.
Direction du champ magnétique terrestre : - Le champ magnétique terrestre trouve son origine dans les mouvements de matière se déroulant à l’intérieur du globe terrestre (courants électriques provoqués par les courants de convection
dans le noyau ; fluide conducteur, principalement du fer en fusion).
-
En un point déterminé de la
surface de la terre, le vecteur champ magnétique terrestre
-
Il est contenu dans un plan vertical,
passant par les pôles magnétiques terrestres, appelé :
-
Plan méridien magnétique.
-
Son pôle Nord s’incline vers
le sol.
-
Sa direction fait avec l’horizontale
un angle i appelé inclinaison (en France, i ≈ 60 °)
-
Ce champ
c
peut être décomposé
en
Remarque : - L’aiguille
aimantée d’une boussole disposée horizontalement n’est sensible qu’à
la composante horizontale
-
Schéma : 2.
On fait passer un courant d’intensité I. a.
Sens du courant dans la bobine.
-
L’aiguille aimantée dévie d’un angle
α : Schéma : b.
Valeur du champ créé par la bobine.
-
Données :
α = 30 ° ; Bh
= 2,0 × 10–5 T. - Valeur du champ résultant :
-
- Comme
-
3.
Dessin de l’aiguille aimantée lorsque l’on
inverse le sens du courant. |
6)- Exercice 29 : Boussole des tangentes :
|
Boussole des tangentes : On utilise un dispositif représenté ci-dessous, constitué d’une
bobine plate de N spires et de rayon R. Au centre de la bobine, sur un support horizontal, se trouve une
aiguille aimantée, mobile autour d’un axe vertical. On peut faire passer dans la bobine un courant d’intensité
réglable grâce à un rhéostat. Lorsque la bobine plate est parcourue par un courant d’intensité
I, le champ magnétique en son centre a une valeur :
Schéma :
1. On veut mesurer la valeur de la composante horizontale Bh du champ magnétique terrestre. Lorsque l’interrupteur est ouvert, on oriente le plan de la bobine dans le plan du méridien magnétique. On ferme K : l’aiguille aimantée tourne d’un angle α = 52 °. Calculer Bh
si N = 5,0, R = 0,12 m et I = 1,0 A. 2. On veut maintenant mesurer la perméabilité magnétique du vide µ0, connaissant la composante Bh = 2,0 × 10–5 T. Chaque fois, on mesure l’angle α dont on a tourné l’aiguille aimantée lors de la fermeture de K. On trouve les valeurs
suivantes :
a.
Calculer, à partir du tableau, les diverses
valeurs de BS créé par la spire en son centre,
ainsi que le produit BS . R. b.
Que peut-on dire de ce produit ? En déduire
une valeur expérimentale de µ0. c.
Comparer à la valeur théorique.
-
Donnée : - μ0 : perméabilité du vide :
-
μ0 = 4 π
x 10–
7 S.I (henry par mètre : H . m–1) |
|
Boussole des tangentes :
-
Schéma :
-
Valeur de
BS :
1.
Valeur de Bh :
-
On veut mesurer la valeur de la
composante horizontale Bh
du champ magnétique terrestre. - Lorsque l’interrupteur K est ouvert, on oriente le plan de la bobine dans le plan du
méridien magnétique.
-
On ferme K : l’aiguille
aimantée tourne d’un angle α = 52 °
ZOOM
-
Cas d’une boussole : - Une boussole se déplace dans un plan horizontal.
-
Elle donne la direction et le sens de
la composante horizontale
-
Une aiguille aimantée mobile sur un
étrier s’oriente selon le champ magnétique terrestre
-
Cas à Paris :
-
Schéma du dispositif à l’équilibre :
-
Valeur de
BS :
-
N = 5, R = 0,12 m et
I = 1,0 A : - Valeur de Bh :
-
Avec :
α = 52 °
2.
Perméabilité magnétique du vide µ0
:
-
Tableau de valeurs :
-
On donne : - Composante horizontale :
-
Bh = 2,0
× 10–5 T. - N = 5,0 ;
R = varie et
I = 1,0 A
-
Chaque fois, on mesure l’angle
α dont on a tourné
l’aiguille aimantée lors de la fermeture de
K. - On trouve les valeurs dans le tableau pour l’angle
α. a.
Les diverses valeurs de BS
créé par la spire en son centre, ainsi que le produit BS
. R.
-
b.
Étude du produit BS .
R :
-
L’analyse du tableau de valeurs : - La valeur du produit BS . R est
constante.
-
BS .
R ≈ 3,14 × 10–6
T . m
-
Comme
N = 5,0 et
I = 1,0 A -
-
Valeur expérimentale de µ0 : - On remarque que le produit :
-
BS .
R ≈ 3,14 × 10–6
T . m
c.
Comparaison avec la valeur théorique.
-
Valeur théorique :
-
μ0théo = 4 π
x 10–
7 S.I (henry par mètre : H . m–1) - μ0théo ≈ 1,256
x 10– 6 S.I
-
μ0théo ≈ 1,26
x 10–
6 S.I - Valeur expérimentale :
-
μ0exp ≈ 1,26
x 10–
6 S.I - Incertitude relative :
-
- Les deux valeurs sont cohérentes.
►
Exploitation des différentes
mesures :
►
Tracé de BS = f
(R) :
-
Graphe :
-
L’exploitation du graphe : - Comme courbe de tendance, on choisit « Puissance »
-
On demande l’affichage :
-
La traduction physique du résultat
mathématique donne : - BS ≈ 3,14 ×
10–6 × R–1
-
Le coefficient de détermination R² =
1,0 - L’adéquation est parfaite entre les deux grandeur.
►
Tracé de BS = f
(1/R) :
-
Graphe :
-
Dans ce cas, la courbe obtenue est
une droite qui passe par l’origine : - L’exploitation du graphe :
-
Comme courbe de tendance, on choisit
« Linéaire » - On demande l’affichage :
-
La traduction physique du résultat
mathématique donne : - BS ≈ 3,14 ×
10–6 × (1/R)
-
Le coefficient de détermination R² =
1,0 - L’adéquation est parfaite entre les deux grandeur.
-
- Avec :
-
|
|
|