QCM N° 02 Caractéristiques des ondes.QCM. Terminale S 2012

QCM N° 02

Caractéristiques des ondes.

QCM N° 02 Caractéristiques des ondes AIDE Pour chaque question, indiquer la (ou les) bonne(s) réponse(s).
	Énoncé	A	B	C	R
1	Une onde ne peut se propager que dans une seule dimension :	Le long d’une corde	Le long d’un ressort	À la surface de l’eau	AB
2	Une onde se propage à la vitesse v = 20 cm / s depuis la source S. Par rapport au point A, le point B est affecté par l’onde avec un retard τ de :	7,5 s	0,30 s	12,5 s	A
3	La longueur d’onde est :	Le nombre de périodes par seconde	L’amplitude de l’onde	La distance parcourue par l’onde durant une période	C
4	La longueur d’onde λ, la fréquence f et la célérité v d’une onde sont liées par la relation :		v = λ . f		AB
5	La fréquence f de l’onde sonore du document ci-dessous vaut :	4,0 x 10³ Hz	8,0 x 10³ Hz	0,25 Hz	A
6	Une onde sonore de fréquence f = 4,0 kHz se propage à 340 m / s. L’ordre de grandeur de sa longueur d’onde est :	10³ m	10 m	10 cm	C
7	La fréquence du fondamental du son du document ci-dessous vaut :	8,8 × 10² Hz	4,4 × 10² Hz	300 mV	B
8	La hauteur d’un son est liée :	À la fréquence du fondamental	Au nombre d’harmoniques	À l’amplitude des harmoniques	A
9	Le chant d’un choriste est perçu avec un niveau d’intensité sonore de 70 dB. Si son voisin se met à chanter de la même manière, le niveau d’intensité sonore sera de :	70 dB	140 dB	73 dB	C
10	La périodicité spatiale d’une onde progressive sinusoïdale est caractérisée par :	Sa fréquence	Sa longueur d’onde	Sa période	B

Questionnaire a été réalisé avec Questy

Pour s'auto-évaluer

AIDE

- Surface de l’eau :

- Le milieu de propagation de la perturbation est le plan d’eau ;

- C’est un milieu à deux dimensions.

- La perturbation se déplace dans toutes les directions à partir du point source S.

- Ressort est tendu horizontalement :

- Le milieu de propagation est unidimensionnel, la direction de propagation est l’axe du ressort.

- Corde tendue horizontalement :

- Le milieu de propagation est unidimensionnel, la direction de propagation est la corde.

- Célérité d’une onde :

- La célérité est le quotient de la distance parcourue sur la durée de parcours.

- célérité v = d / delta t

- Il découle de ceci que pendant la durée d’une période T, l’onde parcourt la distance d égale à la longueur d’onde λ.

- Si v représente la célérité de l’onde, on peut écrire la relation liant ces différentes grandeurs.

λ = v.T	La longueur d’onde λ en mètre (m)
	La célérité de l’onde v en (m / s)
	La période T en seconde (s)

- La longueur d’onde λ est la distance parcourue par l’onde pendant une période T.

- Une onde progressive périodique possède une double périodicité.

- Une périodicité temporelle T est une périodicité spatiale λ.

- Son complexe :

- Un son complexe est formé d’une superposition de vibrations sinusoïdales ayant des amplitudes et des fréquences différentes.

- En 1822, le mathématicien français Joseph FOURIER a montré que :

- Tout signal périodique de fréquence f₁ peut être décomposé en une somme de signaux sinusoïdaux de fréquences f_n multiples de f₁.

- Avec f_n = n.f₁ et n Î N*

- La fréquence f₁ est appelée le fondamental.

- Les fréquences 2 f₁, 3 f₁, …, n.f₁sont appelées harmoniques.

- L’analyse spectrale d’un son permet d’en obtenir le spectre en fréquences.

- Le spectre en fréquences d’un son est la représentation graphique de l’amplitude de ses composantes sinusoïdales en fonction de la fréquence.

- Le niveau d’intensité sonore.

- L’intensité sonore, notée I, caractérise l’intensité du signal reçue par l’oreille.

- Elle s’exprime en watt par mètre carré : W / m² ou W. m^–2

- L’oreille humaine normale perçoit les signaux sonores dont l’intensité est comprise entre

- Une valeur minimale I₀ = 1,0 × 10^–12 W. m^–2 (seuil d’audibilité)

- Et une valeur maximale I_max = 25 W. m^–2 (seuil de douleur).

- Comme l’écart entre ces deux valeurs est très grand, on a créé une nouvelle grandeur, qui utilise une échelle logarithmique, appelée le niveau d’intensité sonore, notée L.

- Relation mathématique :

	Le niveau d’intensité sonore L s’exprime en décibel (dB)
	I caractérise l’intensité du signal en W. m^–2
	I₀ = 1,0 × 10^–12 W. m^–2 (seuil d’audibilité)

- La notation log fait référence à la fonction logarithme décimal.

- Ainsi, l’échelle de niveau d’intensité sonore L varie de 0 dB à environ 140 dB.

- Alors que l’intensité sonore I varie de I₀ = 1,0 × 10^–12 W. m^–2 à 10² W. m^–2

► Quelques propriétés de la fonction logarithme décimal :

- log 1 = 0, log 10 = 1, log 10 ⁿ = n, log 10 ^–ⁿ = –n

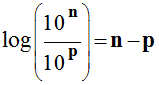
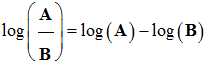
- log

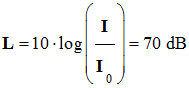
- L = 70 dB

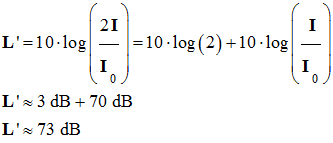
- L' = 73 dB