I- Objectif II- Données. III- Protocole expérimental. IV- Résultats et exploitations. V- Étude complémentaire.

 

►  Matériel pour chaque groupe : calorimètre et accessoires ; un thermomètre ; éprouvette graduée de 250 mL ;

►  Un chronomètre ; une masse marquée en laiton de 200 g.

►  Matériel : un dispositif de chauffage ; un récipient et un support ; un thermomètre.

 

I- Objectif.

  Mesurer la capacité thermique massique du laiton.

II- Données.

III- Protocole expérimental.

 

1)- Première étape :

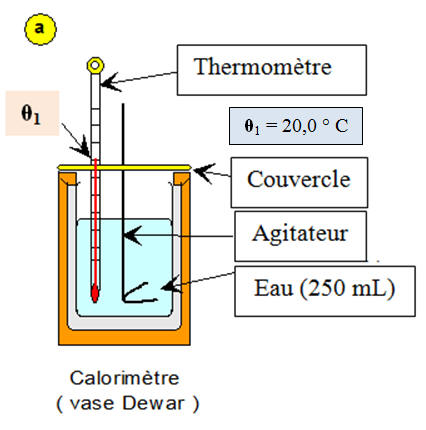
a)-   On chauffe l'eau d'un récipient dans lequel les masses marquées sont immergées.

  Les masses marquées ne doivent pas être en contact avec les parois du récipient (schéma (b)).

b)-  On arrête le chauffage du récipient avant l'ébullition de l'eau.

2)- Deuxième étape :

a)-  Introduire dans un calorimètre une masse d'eau m₁ = 250 g, prise au robinet (schéma (a)).

b)-  Attendre l'équilibre thermique en agitant et mesurer alors la température d'équilibre θ₁ =

3)- Troisième étape :

a)-  Chaque groupe vient avec son calorimètre et ces accessoires à tour de rôle.

b)-  relever la température θ₂ de l'eau qui est aussi celle du métal, prendre une masse marquée et la plonger rapidement dans l'eau du calorimètre (schéma (c)).

c)-  Agiter et relever la température θ toutes les minutes, ceci pendant 15 min.

-  Tableau de valeurs :

t min	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
θ °C	......	.....	.....	.....	.....	.....	.....	.....	.....	.....	.....	.....	.....	.....	.....	.....

IV- Résultats et exploitations.

1)- Faire les schémas des différentes étapes.

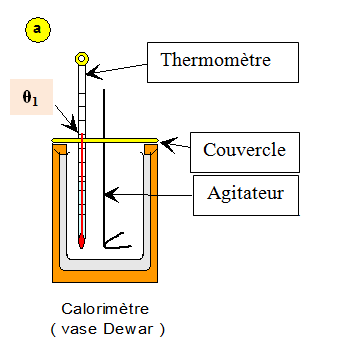
a)-  Première étape :

-  On introduit la masse d'eau m₁ = 250 g dans le calorimètre.

-  On met en place, le thermomètre, l’agitateur et le couvercle.

-  On attend l’équilibre thermique tout en agitant.

-  Valeur de la température : θ₁ = 20,0 ° C.

-  Schéma

 

 

b)-  Deuxième étape :

-  On prend une masse marquée.

-  On note la température de la masse marquée : θ₂ = 80,0 ° C.

-  Schéma :

 

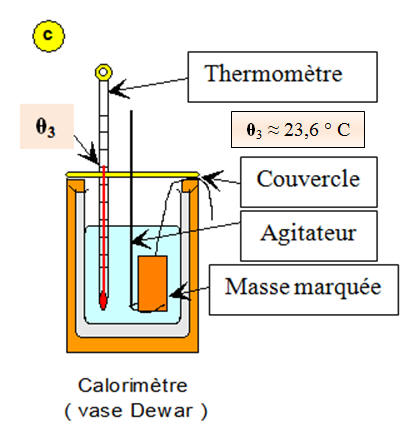
c)-  Troisième étape :

-  On plonge rapidement la masse marquée dans le calorimètre.

-  On met en place le couvercle, le thermomètre et l’agitateur.

-  Tout en agitant, on relève la valeur de la température toutes les minutes.

-  Schéma :

 

2)- Mesures.

a)-  Tracer θ = f (t) et en déduire la température d'équilibre θ₃.

-  Tableau de mesures :

t min	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
θ °C	20,0	21,0	21,5	21,9	22,3	22,6	22,9	23,1	23,3	23,5	23,5	23,6	23,6	23,5	23,5	23,5

-  Graphe : θ = f (t)

 

-  θ₃ = 23,5 ° C.

b)-  Donner les résultats des différentes mesures sous forme de tableau.

3)- Évaluation des transferts d'énergie.

-  Préciser le système étudié en nommant les différentes parties.

-  S₁ : Le calorimètre et ses accessoires :

 

-  S₂ : La masse m₁ = 250 g d’eau.

-  S₃ : La masse m₂ = 200 g de laiton.

-  Le système étudié : S = { S₁ +  S₂+ S₃}

-  Représenter les transferts d'énergie de chaque partie du système sous forme de tableau en indiquant les caractéristiques (température, état physique).

 

 

 

-  Donner l'expression littérale des transferts d'énergie de chaque partie du système.

-  On note :

-  Q_cal l'énergie transférée par le calorimètre et ces accessoires,

-  Q₁ l'énergie transférée par l'eau,

-  Q₂ l'énergie transférée par la masse marquée.

		État initial	État final
Le calorimètre et ses accessoires	Qcal = C (θ3 – θ1)	θ1	θ3
La masse m1 d’eau	Q1= m1 . c1  (θ3 – θ1)	θ1	θ3
La masse m2 de laiton	Q2 = m2 . c2  (θ3 – θ2)	θ 2	θ3

 

-  En appliquant le principe de conservation de l'énergie, déterminer l'équation calorimétrique.

-  Équation calorimétrique :

-  Q_cal  + Q₁ + Q₂ = 0

-  C (θ₃ – θ₁) + m₁ . c₁  (θ₃ – θ₁) + m₂ . c₂  (θ₃ – θ₂) = 0

-  En déduire l'expression littérale de la capacité thermique massique c₂ du laiton.

-  Expression littérale de la capacité thermique massique c₂ du laiton

-   

-  Calculer sa valeur. Donner l'unité.

-  Valeur de la capacité du laiton :

-   

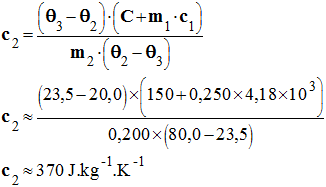
-  Comparer la valeur expérimentale à celle donnée dans le tableau. Conclusion.

-  Comparaison :

-  Incertitude relative sur la valeur de c₂ :

-   

-  La valeur expérimentale est en accord avec la valeur donnée dans le tableau :

-  Remarque :

-  Si pour la valeur de la température d’équilibre, on prend : θ₃ = 23,6 ° C

-  On trouve pour la valeur de la capacité du laiton :

-  c₂ = 381 J.kg^–1.K^–1

-  Exprimer la température d’équilibre θ₃, en fonction de θ₁, θ₂, m₁, m₂, c₁, c₂ et C.

-  Q_cal  + Q₁ + Q₂ = 0

-  C (θ₃ – θ₁) + m₁ . c₁  (θ₃ – θ₁) + m₂ . c₂  (θ₃ – θ₂) = 0

-   

-  Déterminer la valeur de θ₃ à partir de la connaissance des valeurs données dans le tableau et des mesures de θ₁ et θ₂.

-   

V- Étude complémentaire. (à finir)

1)- Déterminer par la méthode de votre choix le volume de la masse marquée.

-  Détermination du volume de la masse marquée :

-  On mesure la hauteur à l’aide d’une règle et le diamètre à l’aide d’un pied à coulisse.

-  H ≈

-  D ≈

-  Volume de la masse marquée :

-   

2)- Déterminer la valeur de la masse volumique du laiton.

-  Masse volumique du laiton :

-   

3)- En déduire la composition massique en cuivre et en zinc du laiton.

-  Composition massique en cuivre et en zinc du laiton :

-   

 

►  Additif :

-  Table de masse volumique du laiton simple en fonction de la teneur en cuivre et zinc.
Les proportions sont en masse.

-  La masse volumique du cuivre vaut 8,920 g . cm^–3.

-  La masse volumique du zinc vaut 7,140 g . cm^–3.

 

 

-  Détermination de la masse volumique du laiton :

-  La formule classique :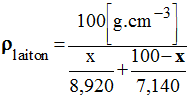  

-   La grandeur x =  % massique cuivre.

-  Cette relation n'est pas correcte, car l'arrangement des atomes de cuivre et de zinc change lors du mélange de ces deux métaux.

-  Une formule empirique donnant de bons résultats pour des proportions de cuivre allant jusqu'à 40 % est :

-   

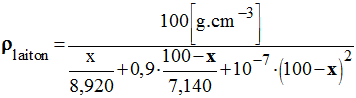
-  La grandeur x =  % massique cuivre

-  Graphe :

 

-  Incertitude relative pour 60 % de cuivre :

-  Formule classique :

-  Formule empirique :

-  Incertitude relative sur les différentes mesures :

-  Hauteur H : mesure au mm

-  Diamètre D : mesure au 1/10^e de mm

-  Conclusion :