|
Partie I : La stabilité est de rigueur
1.
Valeur de la poussée
d’Archimède
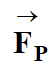 exercée par l’eau sur le plongeur équipé.
exercée par l’eau sur le plongeur équipé.
-
La poussée
d’Archimède exercée
par un fluide de masse volumique
ρfluide
est égale à l’opposé du poids du fluide déplacé.
-
Pour un corps ayant un volume immergé
Vim,
l’expression vectorielle est donnée par la relation suivante :
|
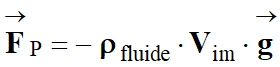
|
|
Point
d’application : centre de poussée C
|
|
Direction : verticale du lieu
|
|
Sens :
vers le haut
|
|
Valeur : FP = ρfluide .
Vim . g
|
-
Dans le cas
présent :
-
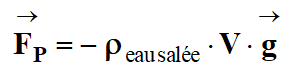
-
Volume du plongeur équipé :
V = 0,088 m3
-
FP
= ρeau
salée .
V .
g
-
FP
= 1,03 × 103 ×
0,088 × 9,81
-
FP
≈ 8,89
× 102 N
-
FP
≈ 8,9 × 102 N
2.
Plongeur équipé à la
profondeur de 20 m et gilet stabilisateur :
-
Le plongeur
est soumis :
-
À la poussée
d’Archimède :
-
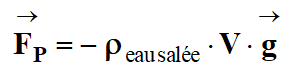
-
FP
≈ 8,9 × 102 N
-
À son poids :
-

-
P
= m
. g
-
P
= 92 × 9,81
-
P ≈
9,02
× 102 N
-
P ≈
9,0 × 102
N
-
En
conséquence :
-
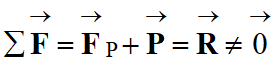
-
Les deux
forces sont verticale et ont des sens opposés.
-
Comme : P > FP
-
La résultante  est une force verticale orientée vers
le bas.
est une force verticale orientée vers
le bas.
-
Le plongeur
n’est pas en équilibre sous l’action des deux forces  : :
-
Il se déplace
vers le bas.
-
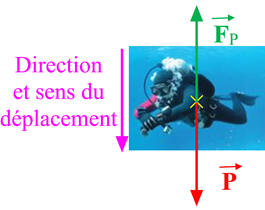
Schéma de la
situation :

-
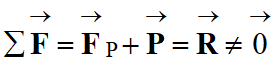
-
De
plus : P > FP
-
Le plongeur
descend verticalement.
3.
Comparaison des
masses volumiques du plongeur équipé et de l’eau salée.
-
Masse
volumique de l’eau salée :
-
ρeau
salée = 1,03 × 103
kg . m–3.
-
Masse
volumique du plongeur équipé :
-
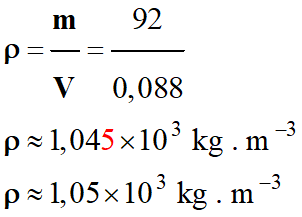
-
Justification
de cette affirmation :
-
Pour répondre
à la question 2., il suffit de comparer les masses volumiques du
plongeur équipé et de l’eau salée :
-
ρ
> ρeau
salée
-
le plongeur
descend.
-
Or
-
P
= m
. g
-
P
= ρ
.
V .
g
-
D’autre part :
-
FP
= ρeau
salée .
V .
g
-
On tire :
-
P
–
FP
= ρ
.
V .
g –
ρeau
salée .
V .
g
-
P
–
FP
= V
.
g . (ρ –
ρeau
salée)
-
Si
ρ >
ρeau
salée , alors
P
> FP
et le plongeur descend.
-
Si
ρ <
ρeau
salée , alors
P
< FP
et le plongeur monte.
-
Si
ρ =
ρeau
salée , alors
P
= FP
et le plongeur est en équilibre
4.
Volume d’air
nécessaire pour la stabilisation :
-
Pour que le
plongeur soit en équilibre, il faut que :
-

-
Il faut donc
que :
-
P
= ρ
.
Vim
.
g =
FP
= ρeau
salée .
Vim
. g
-
Il faut faire
varier le volume immergé du plongeur pour que :
-
Le volume immergé
Vim
du plongeur doit augmenter pour faire diminuer sa masse volumique
globale.
-
Ainsi
-
ρplongeur
= ρeau
salée
-
Or, la masse
du plongeur ne varie pas :
-
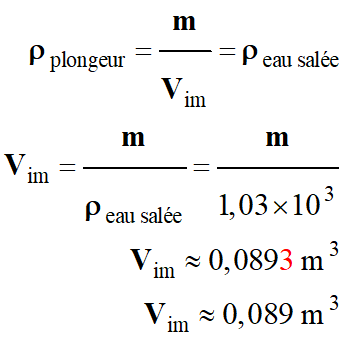
-
Variation de
volume :
-

-
Le plongeur
doit « injecter 1,3 L d’air » dans son gilet de stabilisation (il faut
tenir compte de la pression à 20 m sous l’eau).
-
Le volume du
gilet de stabilisation doit augmenter de 1,3 L.
Partie II : Les courants sous-marins et les
ordinateurs de plongée.
1.
Valeur
v2
de la vitesse de l’eau dans le passage de diamètre
d2
-
Cylindre 1 :
d1
= 6,0 m et v1
= 0,30 m . s–1
-
Cylindre 2 :
d2
= 3,0 m
-
Schéma de la
situation :

-
L’eau est
considérée comme un fluide incompressible qui s’écoule en régime
permanent indépendant du temps.
►
Débit
volumique DV
:
-
Le débit volumique
DV
est égal au produit de la surface
S
de la section de tube traversée par le fluide, par la valeur
v
de la vitesse du fluide au niveau de cette section.
|
DV
= S . v
|
DV :
Débit volumique (m3 . s–1)
|
|
S :
surface de la section de tube traversée par le fluide (m2)
|
|
v
: valeur de la vitesse du fluide au niveau de cette section
(m . s–1)
|
-
Dans le cas
présent :
-
DV
= S1
. v1
= S2
. v2
-
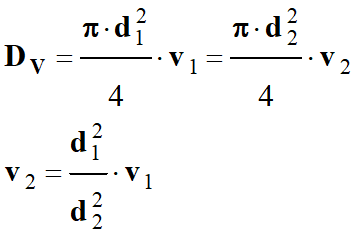
-
Application
numérique :
-
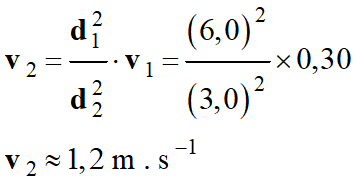
2.
Différence de
pression ΔP
= P2
– P1
entre les deux passages cylindriques de la cavité
-
Les points
1 et
2
appartiennent à la même ligne de courant :
-
On considère
que la relation de Bernoulli peut s’appliquer le long d’une ligne de
courant d’un fluide incompressible en écoulement permanent indépendant
du temps.
-
Relation de
Bernoulli :
-
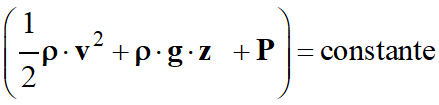
-
Le long de la
ligne de courant, les points 1
et 2
sont à la même altitude :
-
z
= z1
= z2.
-
En utilisant
le fait que : z1
= z2
=> ρeau salée .
g .
z1
= ρeau
salée .
g .
z2
-

-
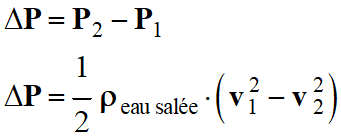
-
Application
numérique :
-
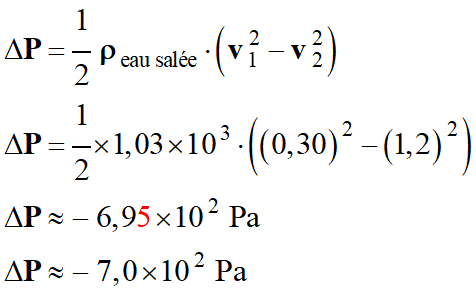
-
La pression est plus faible au point
2
qu’au point 1.
3.
Différence de
profondeur, entre les deux passages cylindriques de la cavité, indiquée
par l’ordinateur:
-
La pression
dans l’eau augmente de 1 bar lorsque la profondeur augmente de 10 m.
-
1 bar
= 1,0 × 105
Pa
-
La différence de pression est de 7,0 ×102
Pa
-
Loi
fondamentale de la statique des fluides :
-
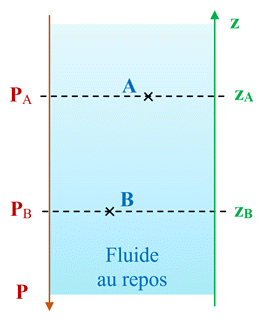
Relation :
|
PB
– PA
= ρ . g . ( zA
– zB)
|
|
P :
Pression en pascal (Pa)
|
|
ρ
: masse volumique du fluide
au repos
(kg . m–3)
|
|
g :
intensité de la pesanteur (N . kg–1)
|
|
z :
coordonnée verticale (m)
L’axe des
coordonnées verticales
est
orienté vers le haut
|
-
Schéma :
-
Tableau :
|
Différence
de
pression
|
Différence
de
profondeur
|
|
7,0 ×102
Pa
|
Δz
|
|
1,0 × 105
Pa
|
10m
|
|

|
-
La diminution de la pression de
|ΔP|
= 7,0 ×102
Pa, liée à la présence d’un courant sous-marin,
entraîne une erreur sur
la mesure de la profondeur par l’ordinateur de 7,0 cm.
|