|
|
Modélisation de l’écoulement d’un fluide Exercices |
|
|
|
|
|
QCM r
Modélisation de
l’écoulement d’un fluide
La Poussée
d’Archimède
La conservation
du débit volumique
La relation de
Bernoulli |
1)- Exercice 05 page 288 : Expression vectorielle de la poussée d’Archimède :
|
Expression vectorielle de la poussée d’Archimède : Un iceberg immobile de volume Vice flotte à la surface de l’eau. Son volume immergé est Vim.
1.
Représenter les deux forces exercées sur
l’iceberg. 2.
Écrire l’expression vectorielle de ces deux
forces en utilisant les notations du texte et calculer leurs
valeurs.
-
Données :
-
Volumes :
-
Vice = 7,0 ×
104 m3 ;
Vim = 6,3 ×
104 m3
-
Masses volumiques :
-
ρice = 9,2 ×
102 kg . m–3 ;
ρeau = 1,02 ×
103 kg . m–3
-
Intensité de la pesanteur : g = 9,81
N . kg–1. |
|
Expression vectorielle de la poussée d’Archimède : 1.
Représentation des deux forces exercées sur
l’iceberg.
-
Schéma 01 :
-
Schéma 02 :
-
Principe de l’Inertie :
-
Énoncé : Principe d’Inertie :
-
Autre formulation :
-
Réciproque du principe
d’Inertie :
-
Dans le cas présent, l’iceberg flotte
et il est immobile.
-
-
Les deux forces ont :
-
Même direction, des sens opposés et
la même valeur. 2.
Expression vectorielle de ces deux forces.
-
Poids de l’iceberg :
-
Poussée d'Archimède :
-
Calcul des valeurs
-
Poids de l’iceberg :
-
P = ρice
. Vice . g = 9,2 × 102 × 7,0 ×
104 × 9,81
-
P ≈ 6,31
× 108 N
-
P ≈ 6,3 × 108
N
-
Poussée d’Archimède :
-
FP = ρeau
. Vim . g = 1,02 × 103 × 6,3 ×
104 × 9,81
-
FP ≈ 6,30
× 108 N
-
FP ≈ 6,3 × 108
N
-
Le résultat est en accord avec le
principe de l’Inertie.
-
L’iceberg est bien en équilibre. |
2)- Exercice 07 page 288 : Définir le débit volumique d’un fluide :
|
Définir le débit volumique d’un fluide : 1.
Quand dit-on qu’un fluide s’écoule en régime
permanent indépendant du temps ? 2.
Définir le débit volumique d’un fluide. |
|
Définir le débit volumique d’un fluide : 1.
Fluide en régime permanent indépendant du
temps :
-
Un fluide s’écoule en régime
permanent indépendant du temps, si la valeur v de la
vitesse en chaque position est indépendante du temps
t.
-
En régime permanent, la valeur
v de la vitesse d’écoulement en tout point ne varie pas au cours du temps
t.
-
En régime permanent, en tout point
-
Ainsi, en régime permanent,
au point M1
du fluide, la valeur de la vitesse v1
ne change pas au cours du temps.
-
De même au point M2
du fluide la valeur de la vitesse v2 ne change pas
au cours du temps. 2.
Définition du débit volumique d’un fluide.
-
En régime permanent, le débit
volumique DV
d’un fluide correspond au volume V de fluide
qui traverse une section droite
S pendant une durée
Δt.
-
Relation :
-
Le débit volumique
DV est une caractéristique de l’écoulement d’un fluide.
-
Conséquence :
-
Pendant la durée
Δt :
-
Le fluide traverse une section de
surface S ;
-
Le fluide parcourt la distance
ℓ avec la vitesse
d’écoulement v :
-
ℓ
= v .
Δt
-
On en déduit l’expression du volume
V de fluide écoulé à
travers la section S :
-
V = S . ℓ
-
V = S . v .
Δt
-
Schéma :
-
On en déduit la relation suivante :
-
►
Débit volumique DV
:
-
Le débit volumique
DV est égal au produit de la surface
S de la section de tube
traversée par le fluide, par la valeur
v de la vitesse du fluide
au niveau de cette section.
|
3)- Exercice 09 page 288 : Traduire la conservation d’un débit volumique :
|
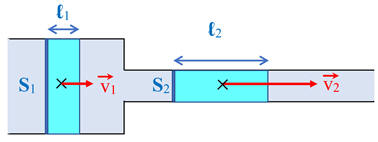
Traduire la conservation d’un débit volumique : De l’eau liquide, fluide incompressible, s’écoule en régime
permanent indépendant du temps dans une canalisation.
L’eau qui traverse la section de surface S1
parcourt la distance ℓ1 pendant la durée Δt. L’eau qui traverse la section de surface S2,
pendant la même durée Δt, parcourt la distance ℓ2. 1.
Comparer les débits volumiques aux deux
extrémités du tube schématisées ci-dessus. 2.
Exprimer la valeur v2 de
la vitesse en fonction de v1, S1
et S2. La calculer.
-
Données :
-
Surface des sections :
S1 =30 cm2 ;
S2 =10 cm2
-
Valeur de la vitesse d’écoulement du
fluide : v1 =
2,2 m s–1. |
Traduire la conservation d’un débit volumique : 1.
Comparaison des débits volumiques aux deux
extrémités du tube :
-
Schéma :
-
L’eau liquide, fluide incompressible,
s’écoule en régime permanent indépendant du temps dans une canalisation :
-
Au cours d’un écoulement en régime
permanent, le débit volumique d’un fluide incompressible se conserve. Il ne varie pas.
-
Pour un fluide incompressible, le
débit volumique DV
est le même en tout point du fluide.
-
DV =
DV1 =
DV2 2.
Expression de la valeur v2
de la vitesse en fonction de v1, S1
et S2.
-
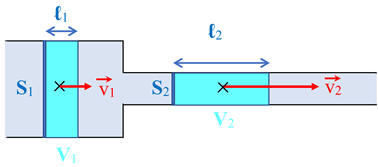
Schéma :
-
Le volume
V1 de fluide
se déplaçant dans la canalisation de section
S1 est identique au volume V2 de fluide se déplaçant dans la canalisation de section
S2
ceci pendant la même durée
Δt.
-
V1 =
V2
-
Avec :
-
V1 =
S1 .
ℓ1 et
V2 = S2
. ℓ2
-
Et d'autre part :
-
ℓ1 =
v1 .
Δt et
ℓ2 = v2
. Δt
-
En conséquence, pendant la durée
Δt :
-
-
De même :
-
DV2 =
S2 .
v2
-
Comme le débit est constant :
-
DV =
S1 . v1
= S2 .
v2 -
-
Valeur de la vitesse :
-
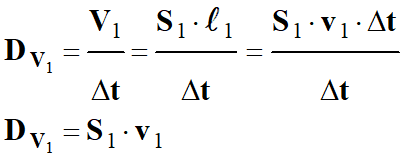
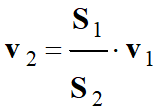
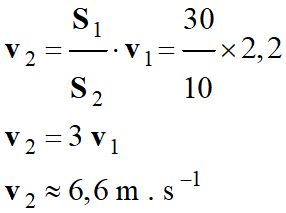
![]()
4)- Exercice 11 page 289 : Décrire les grandeurs physiques de la relation de Bernoulli :
|
Décrire les grandeurs physiques de la relation de Bernoulli : 1.
Décrire chaque grandeur qui intervient dans
la relation de Bernoulli. Préciser les unités. 2.
À l’aide de cette relation, écrire une
égalité faisant intervenir des grandeurs physiques en deux positions A et B
d’une ligne de courant horizontale d’un fluide.
-
Donnée :
-
On considère que la relation de
Bernoulli peut s’appliquer le long d’une ligne de courant d’un fluide incompressible en écoulement permanent indépendant du
temps
-
Elle s’écrit :
-
|
Décrire les grandeurs physiques de la relation e Bernoulli : 1.
Relation de Bernoulli et unités.
ρ :
masse volumique du fluide
(kg . m–3 )
P :
pression du fluide au point considéré (Pa)
v
: vitesse du fluide au point considéré (m . s–1)
g :
intensité de la pesanteur :
g
= 9,81 N. kg–1 ou g = 9,81 m.
s–2
z :
altitude au point considéré (m)
Constante : (J . m–3) 2.
Relation en deux positions A et B
d’une ligne de courant horizontale d’un fluide.
-
Schéma :
-
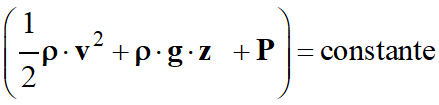

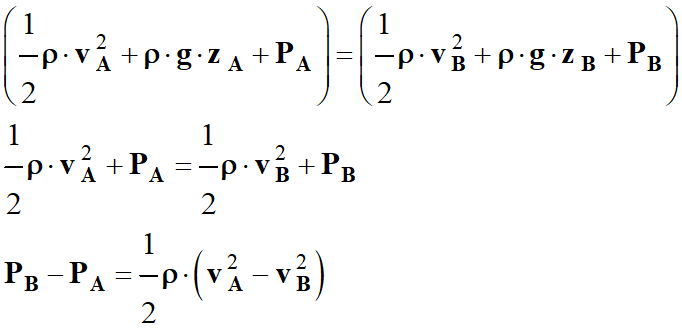
![]()
5)- Exercice 12 page 289 : Exploiter qualitativement la relation de Bernoulli :
|
Exploiter qualitativement la relation de Bernoulli : À l’aide de la relation de Bernoulli, compléter les phrases
suivantes, les positions A et B étant situées sur une même
ligne de courant. a.
Si vA > vB
et si zA = zB, alors la pression
PA à la position A … b.
Si vA < vB
et si PA = PB, alors la
coordonnée verticale zA est … c.
Si vA = vB
et si zA < zB, alors la pression
PA à la position A est …
-
Donnée :
-
On considère que la relation de
Bernoulli peut s’appliquer le long d’une ligne de courant d’un fluide incompressible en écoulement
permanent indépendant du temps
-
Elle s’écrit :
-
|
|
Exploiter qualitativement la relation de Bernoulli :
-
Relation de Bernoulli :
-
-
Le long d’une ligne de courant d’un
fluide incompressible en écoulement permanent indépendant du temps :
-
a.
Si vA > vB
et si zA = zB, alors la pression
PA à la position A est inférieure à la
pression PB à la position
B.
-
-
vA >
vB =>
PB –
PA > 0 => PB
> PA
b.
Si vA < vB
et si PA = PB, alors la
coordonnée verticale zA est
supérieure à la
coordonnée verticale zB.
-
-
vA <
vB et si
PA =
PB => zB
– zA < 0 => zB <
zA c.
Si vA = vB
et si zA < zB, alors la pression
PA à la position A est
supérieure à la
pression PB à la position
B.
-
-
vA =
vB et
zA <
zB => zA
– zB < 0 =>
PB –
PA < 0 => PB
< PA |
6)- Exercice 13 page 289 : Exploiter la relation de Bernoulli :
|
Exploiter la relation de Bernoulli : Un écoulement de lait est schématisé ci-dessous.
-
Calculer la pression
PB en B.
-
Donnée :
-
On considère que la relation de
Bernoulli peut s’appliquer le long d’une ligne de courant d’un
fluide incompressible en écoulement permanent indépendant du temps.
-
Elle s’écrit :
-
|
|
Exploiter la relation de Bernoulli :
-
Relation de Bernoulli :
-
-
On considère que le lait est un
fluide incompressible en écoulement permanent indépendant du temps.
-
Le long de la ligne de courant, les
points A et
B sont à la même altitude :
-
z =
zA =
zB.
-
On peut utiliser la relation de
Bernoulli :
-
En utilisant le fait que :
zA =
zB => ρ .
g .
zA = ρ .
g .
zB
-
-
Valeur de la pression
PB en B.
-
-
Remarque : PB <
PA |
7)- Exercice 17 page 290 : Du yaourt au miel :
|
Du yaourt au miel : Dans une laiterie, afin d’aromatiser des yaourts, du miel s’écoule d’un réservoir dans une cuve contenant du lait à travers un tuyau de diamètre
d = 12,5 mm, suivant le schéma ci-dessous. Le miel est considéré comme un fluide incompressible dont on
néglige la viscosité. Le réservoir est parallélépipédique et de grandes dimensions par
rapport à celles de la cuve. 1. La durée de remplissage de la cuve d’un volume V = 41 L de miel est Δt = 2,0 min. Calculer le débit volumique DV
d’écoulement du miel dans la cuve en m3 . s–1. 2.
Calculer la valeur vS de
la vitesse d’écoulement du miel dans le tuyau. 3. La valeur de la vitesse du miel en A est considérée comme négligeable devant la valeur de la vitesse du miel dans le tuyau. Exprimer puis calculer la coordonnée verticale zA
de la position A.
-
Données :
-
Masse volumique du miel : ρmiel
= 1042 kg . m–3.
-
Intensité de la pesanteur :
g = 9,81 N . kg–1.
-
On considère que la relation de
Bernoulli peut s’appliquer le long d’une ligne de courant d’un fluide incompressible en écoulement permanent
indépendant du temps.
-
Elle s’écrit :
-
|
|
Du yaourt au miel :
1.
Débit volumique
DV d’écoulement du miel dans la cuve en m3
. s–1.
-
La durée
de remplissage de la cuve :
Δt = 2,0 min.
-
Cuve d’un
volume V = 41 L
-
En régime
permanent, le débit volumique
DV d’un fluide correspond au volume
V de fluide qui traverse
une section droite S
pendant une durée Δt.
-
Relation :
-
Le débit
volumique DV est une caractéristique de l’écoulement d’un fluide.
-
Dans le
cas présent :
-
2.
Valeur vS
de la vitesse d’écoulement du miel dans le tuyau.
-
Tuyau de
diamètre d = 12,5 mm
-
Surface
S de la section du tuyau
-
►
Autre
expression du débit volumique DV :
-
Le débit
volumique DV est égal au produit de la surface
S de la section de tube
traversée par le fluide, par la valeur
vS de la
vitesse du fluide au niveau de cette section.
-
3.
. Expression de
la coordonnée verticale zA de la position A.
-
Le miel
est considéré comme un fluide incompressible dont on néglige la
viscosité.
-
Les deux
points A et S appartiennent à la
même ligne de courant.
-
On peut
utiliser la relation de Bernoulli :
-
-
Relation
que l’on applique aux deux points considérés :
-
-
Expression de la coordonnée verticale
zA de la
position
A :
-
-
Application numérique :
-
On
remarque que : PA = PS
= Patm =>
PA –
PS = 0
-
D’autre
part :
-
La valeur
de la vitesse du miel en A
est considérée comme négligeable devant la valeur de la vitesse du
miel dans le tuyau.
-
-
Valeur de
la coordonnée verticale zA
de la position A
-
|
8)- Exercice 23 page 292 : Euréka :
|
Euréka : Le roi Hiéron II, tyran de Syracuse au IIIe siècle avant notre ère, soupçonne l’orfèvre qui a fabriqué sa couronne, censée être en or massif, d’y avoir mis un mélange d’or et d’argent. La couronne a bien la même masse que l’or fourni à
l’orfèvre pour la réalisation, mais le roi demande tout de même à Archimède de
vérifier s’il y a tromperie, sans abîmer la couronne. Alors qu’Archimède, aux bains publics, se plonge dans un bain
chaud et le fait déborder, il s’écrie soudainement : « Eurêka, Eurêka ! » (« j’ai
trouvé ! ») Il court nu - dit la légende -, jusqu’à son habitation pour
énoncer : « Un corps plongé dans un liquide déplace un volume de ce
liquide égal à son propre volume » Par comparaison des volumes d’eau déplacée par la couronne et par
le volume équivalent d’or, il pourra trancher.
1.
Les volumes : a.
Calculer le volume V1
d’une couronne en or massif de masse m = 2,00 kg. b.
Montrer que le volume V2
de cette couronne est 1,12 × 10–1 L si l’orfèvre a
substitué 10 % en masse d’or par de l’argent. c.
Justifier qu’il est peu probable
qu’Archimède ait pu conclure en réalisant l’expérience qu’il
imagine. 2.
Expérience : a. On conçoit une autre expérience en immergeant complétement la couronne dans un récipient contenant de l’eau. Indiquer les
caractéristiques de la poussée d’Archimède
b.
Répondre à la même question si l’orfèvre a
substitué 10 % de la masse d’or par de l’argent. 3.
Calculer la valeur du poids de la couronne
en or massif de masse m. 4.
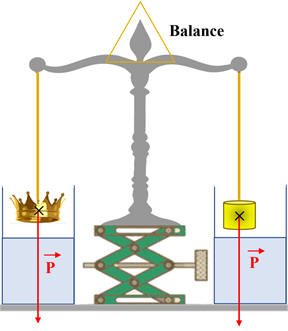
Lors de l’expérience schématisée ci-dessous,
prévoir de quel côté penche le fléau de la balance lorsque des deux objets, de même
masse, sont immergés.
-
Données :
-
Masses volumiques :
-
ρargent = 1,050 ×
104 kg . m–3 ;
-
ρor = 1,930 × 104
kg . m–3 ;
-
ρeau = 1,000 × 103
kg . m–3 ;
-
intensité de la pesanteur : g
= 9,81 N . kg–1. |
Euréka : 1.
Les volumes : a.
Volume V1 d’une couronne
en or massif.
-
masse m = 2,00 kg
-
Masse volumique de l’or : ρor
= 1,930 × 104 kg . m–3
-
b.
Volume V2 de la couronne
si l’orfèvre a substitué 10 % en masse d’or par de l’argent.
-
Masse d’argent :
-
-
D’autre part :
-
mAg = ρAg
. VAg
-
Masse d’or :
-
-
D’autre part :
-
mor = ρor
. Vor
-
Volume V2 de la couronne en alliage :
-
-
Application numérique :
-
-
Ce résultat est bien en accord avec
celui de l’énoncé
-
V2 = 1,12 × 10–1
L c.
Expérience imaginée par Archimède.
-
Par comparaison des volumes d’eau
déplacée par la couronne et par le volume équivalent d’or, il pourra
trancher.
-
L’écart entre les deux volumes
V1 et
V2 est très faible (pour l’époque).
-
V2 –
V1 ≈ 112 – 104
-
V2 –
V1 ≈ 8 mL 2.
Expérience : a.
Caractéristiques de la poussée
d’Archimède
-
Poussée d’Archimède :
Point d’application : centre de poussée C
Direction : verticale du lieu
Sens : vers le haut
Valeur : FP = ρeau .
V1 . g
-
Dans le cas présent :
-
Valeur de la poussée d’Archimède :
-
FP = ρeau
. V1 . g
-
FP ≈ 1,000 × 103
× 1,04 × 10–4 × 9,81
-
FP ≈ 1,016
N
-
FP ≈ 1,02 N b.
Caractéristiques de la poussée d’Archimède
-
Poussée d’Archimède :
Point
d’application : centre de poussée C
Direction : verticale du lieu
Sens : vers le haut
Valeur : F’P = ρeau
. V2 . g
-
Dans le cas présent :
-
Valeur de la poussée d’Archimède :
-
F’P
= ρeau . V2 . g
-
F’P
≈ 1,000 × 103 × 1,12 × 10–4 × 9,81
-
F’P
≈ 1,101 N
-
F’P
≈ 1,10 N 3.
Valeur du poids de la couronne en or massif
de masse m.
-
P =
m .
g
-
P = 2,00 × 9,81
-
P = 19,62
N
-
P = 19,6 N 4.
Prévoir de quel côté penche le fléau de la
balance lorsque des deux objets, de même masse, sont immergés.
-
Au départ, la balance est en
équilibre (on peut négliger la poussée d’Archimède due à l’air
devant le poids de la couronne)
-
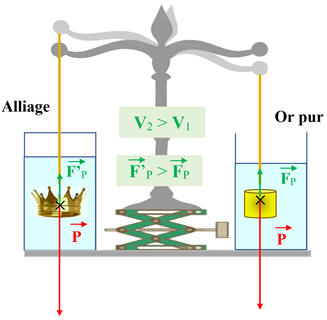
On plonge la couronne en alliage et l'objet en or
massif dans l’eau :
-
Comme
V2 >
V1, alors F’P
> FP
-
Schéma de la situation :
-
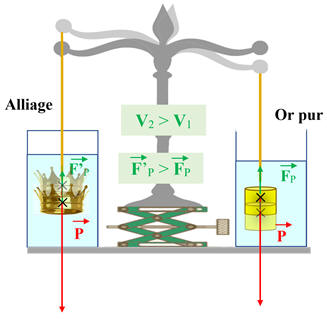
Le poids est le même de chaque côté.
-
Comme l’objet en alliage à un volume
supérieur à l’objet en or pur, la poussée d’Archimède
-
La balance à fléau étant très
sensible, l’équilibre est rompu.
-
Le fléau de la balance penche du côté
de l’objet en or pur.
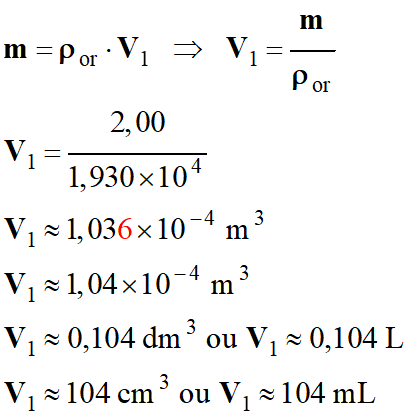
![]()
![]()

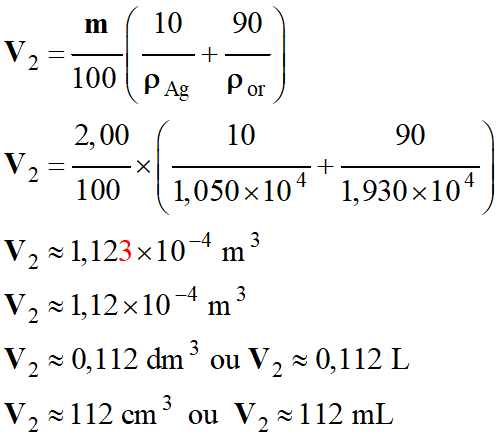
![]() exercée par l’eau sur la couronne si elle est en or
massif.
exercée par l’eau sur la couronne si elle est en or
massif.
![]()
![]() si l’orfèvre a substitué 10 % de la masse d’or par de
l’argent.
si l’orfèvre a substitué 10 % de la masse d’or par de
l’argent.
![]()
![]() est supérieure à la poussée d’Archimède
est supérieure à la poussée d’Archimède
![]() .
.![]()
9)- Exercice 26 page 294 : Sonde Pitot :
|
Sonde Pitot : Un hors-bord est équipé notamment d’une sonde Pilot qui permet
de déterminer la valeur v de sa vitesse. Cette sonde, placée sur la coque du bateau, est immergée.
L’eau est considérée comme un liquide incompressible. A.
Applications des sondes Pitot. Une sonde de Pilot (Henri Pitot, 1665-1771) sert à mesurer la valeur de la vitesse d’un écoulement de fluide. Inventée en 1732, elle a été ensuite améliorée par Henry Darcy, puis Ludwig Prandtl. Actuellement les sondes de Pitot sont fréquemment utilisées pour mesurer la valeur de
la vitesse d’un avion ou d’un bateau. B.
Schéma de principe d’une sonde de Pitot. Dans un référentiel lié au bateau, l’eau se déplace à une vitesse de valeur v. Son vecteur vitesse représenté sur le schéma est orienté vers la droite. Dans un référentiel lié à l’eau supposée immobile, le bateau
se déplace à une vitesse de même valeur v. Le vecteur vitesse du bateau est, lui,
orienté vers la gauche. La différence de coordonnées verticales entre O et O’, ou entre A et B est négligeable. 1.
Vitesse et pression : a.
Justifier que les pressions en O’ et
B sont identiques. b. La position A est appelée point d’arrêt : la valeur de la vitesse du fluide y est nulle. Le long de la ligne de courant 2, justifier que PA est
supérieure à PO. c.
En déduire que la valeur v de la
vitesse en O est :
2. La différence de pression mesurée par le manomètre différentiel est ΔP = 3,30 × 103 Pa. Calculer la valeur v de la vitesse du hors-bord. 3. La limitation de vitesse dans la zone de navigation est 5 nœuds. Le hors-bord est-il en infraction ?
-
Données :
-
Masse volumique de l'eau : ρeau
= 1,000 × 103 kg . m–3.
-
Intensité de la pesanteur : g
= 9,81 N . kg–1.
-
1 nœud = 1 mile marin par heure =
1,852 km . h–1
- On considère que la relation de Bernoulli peut s’appliquer le long d’une ligne de courant d’un fluide incompressible
en écoulement permanent indépendant du temps.
-
Elle s’écrit : -
|
Sonde Pitot : 1.
Vitesse et pression : a.
Valeur des pressions en O’ et B.
-
Schéma :
-
L’eau est considérée comme un liquide
incompressible.
-
La différence de coordonnées
verticales entre O et O’, ou entre A et B
est négligeable.
-
La différence de coordonnées
verticales entre O’ et B est négligeable :
-
La relation de Bernoulli permet
d’écrire que :
-
-
D’autre part : pour le point
O’
-
-
Or
vO=
vB =
vO’ = v et
zO =
zB ≈ zO’
= zA =
z
-
-
Pour le point
O’ :
-
-
On en déduit la relation suivante :
-
PO’ ≈
PB
-
La pression au point
B est pratiquement identique à celle du point
O’.
-
Dans le cas présent, on peut
considérer que les points O’
et B appartiennent à la même ligne de courant. b.
Comparaison de PA et PO.
-
La position
A est appelée point
d’arrêt : - La valeur de la vitesse du fluide y est nulle :
-
Pour la ligne de courant 2, on peut
écrire :
-
-
Or
vO’ =
v et vA
= 0;
-
zO’ =
zA
-
-
On en déduit que
PA > PO
-
Car : c.
Valeur v de la vitesse en O :
-
Or
PB =
PO
-
De plus :
-
-
On retrouve bien la relation de
l’énoncé.
-
2.
. Calculer la valeur v de la vitesse
du hors-bord.
-
La différence de pression mesurée par
le manomètre différentiel :
-
ΔP = PA
– PB= 3,30 × 103 Pa
-
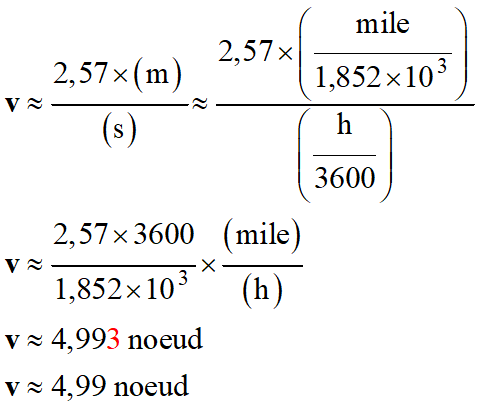
3.
Vitesse du hors-bord en nœud.
-
1 nœud = 1 mile marin par heure =
1,852 km . h–1
-
1 mile marin = 1,852 km = 1,852 × 103
m
-
-
Le hors-bord est à la limite de
l’infraction, mais il n’est pas en infraction.
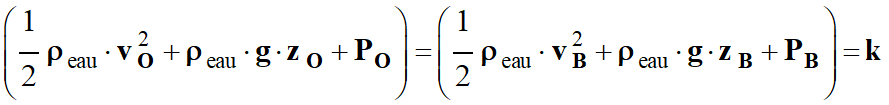

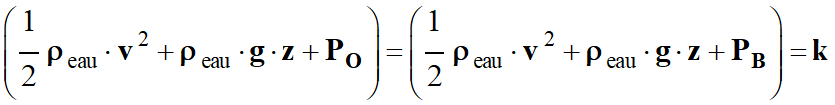
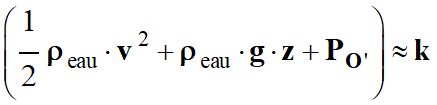
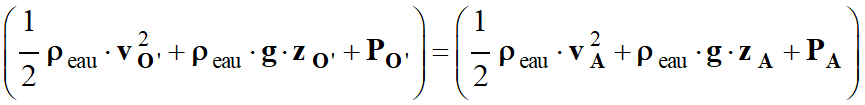

![]()
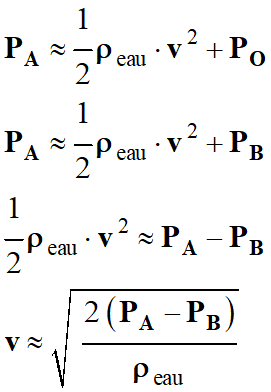

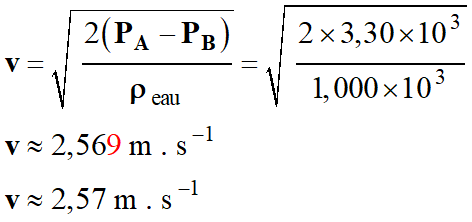
![]()
|
|