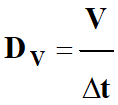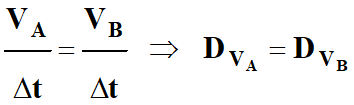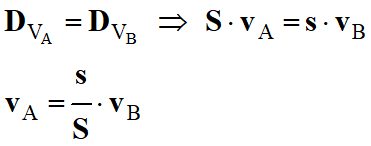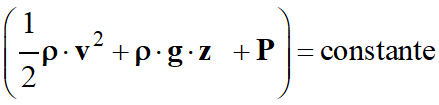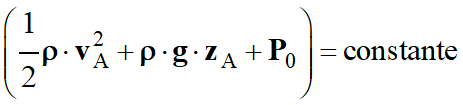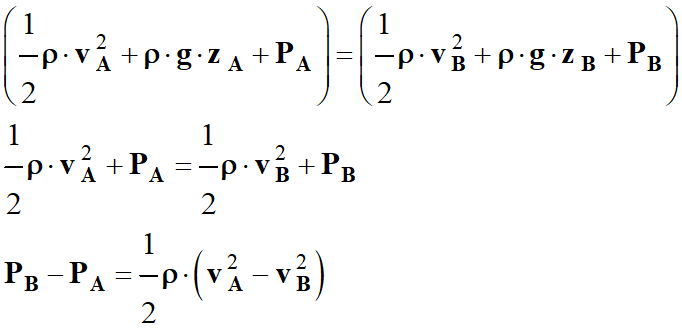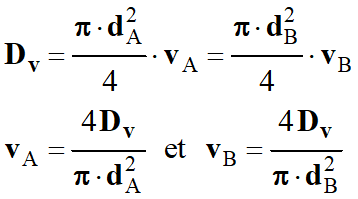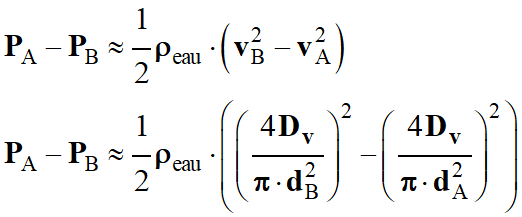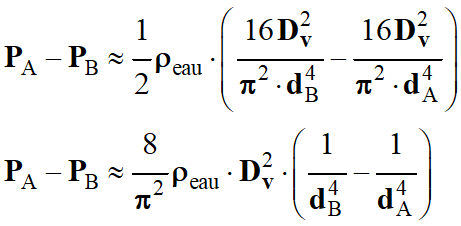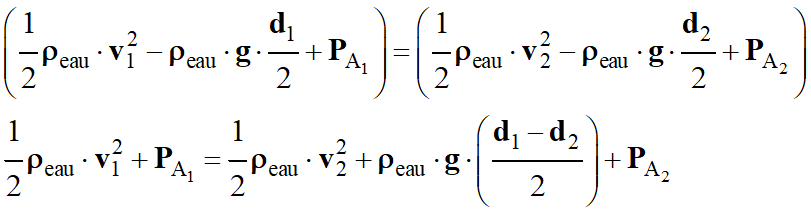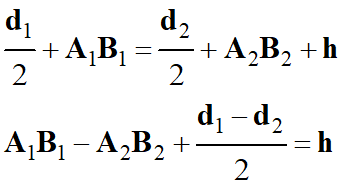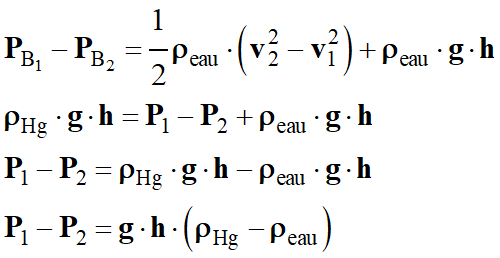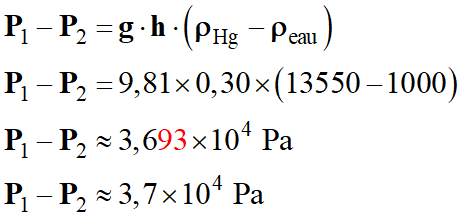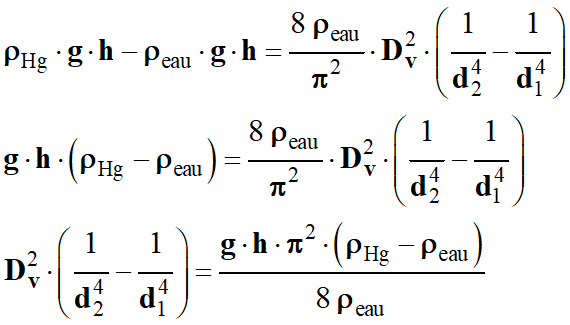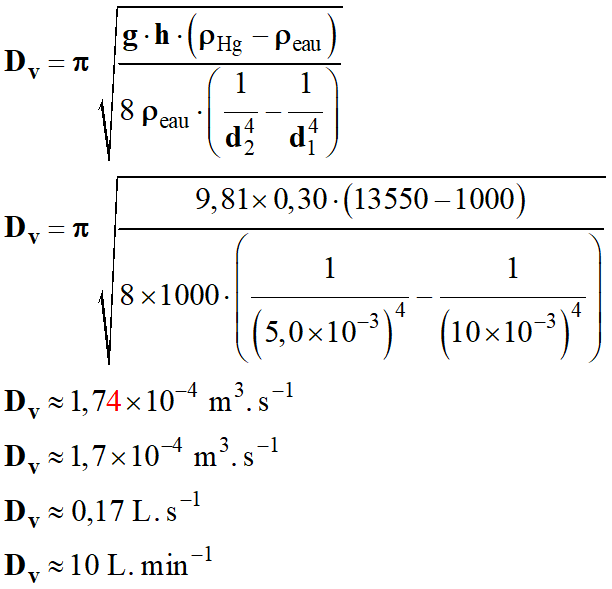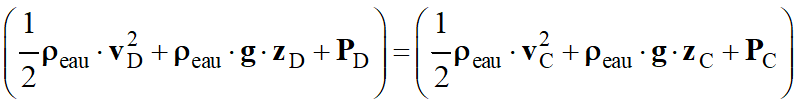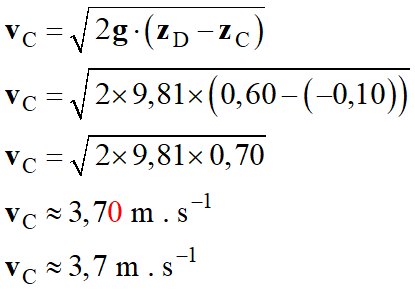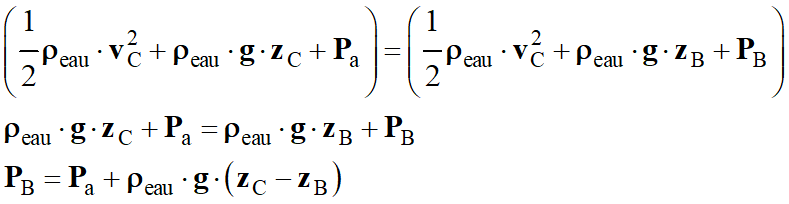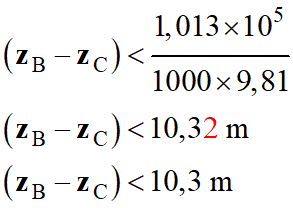Chap N° 14 Exercices 2024 : Modélisation de l’écoulement d’un fluide

Chap. N°14

Modélisation de l’écoulement d’un fluide

Exercices 2024
Cours.

Exercices

I- Exercice : Calculer une vitesse d’éjection de vidange.

1)- Énoncé.

2)- Correction.

II- Exercice : Trompe à eau.

1)- Énoncé.

2)- Correction.

III- Exercice : Tube de Venturi.

1)- Énoncé.

2)- Correction.

IV- Exercice : Siphon.

1)- Énoncé.

2)- Correction.

I- Exercice : Calculer une vitesse d’éjection de vidange.

1)- Énoncé.

La vidange d'un réservoir d'eau est représentée ci-dessous.

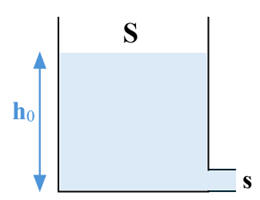
réservoir

La section de l'ouverture de vidange s est très petite devant la surface libre S du liquide, ce qui permet en première approximation de supposer la surface libre du liquide immobile.

- Exprimer puis calculer la vitesse d'écoulement du liquide par la section s pour h₀ =1,0 m.

2)- Correction.

- Vitesse d'écoulement du liquide par la section s pour h₀ =1,0 m.

- Schéma :

réservoir et légende

► Débit volumique.

- En régime permanent, le débit volumique D_V d’un fluide correspond au volume V de fluide qui traverse une section droite S pendant une durée Δt.

- Relation :

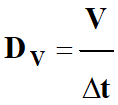
	D_V : Débit volumique (m³ . s^–1)
	V : Volume de fluide (m³)
	Δt : durée (s)

- Le débit volumique D_V est une caractéristique de l’écoulement d’un fluide.

- Dans le cas présent :

- Le volume V_A de fluide se déplaçant dans la canalisation de section S est identique au volume V_B de fluide se déplaçant dans la canalisation de section s ceci pendant la même durée Δt.

- V_A = V_B

- En conséquence, pendant la durée Δt :

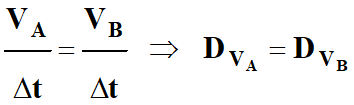
- relation

- D_V = D_VA = D_VB

► Débit volumique D_Vet vitesse

- Le débit volumique D_V est égal au produit de la surface S de la section de tube traversée par le fluide, par la valeur v de la vitesse du fluide au niveau de cette section.

D_V = S . v	D_V : Débit volumique (m³ . s^–1)
	S : surface de la section de tube traversée par le fluide (m²)
	v : valeur de la vitesse du fluide au niveau de cette section (m . s^–1)

- Schéma :

réservoir et légende

- Au point A : D_VA = S . v_A

- Au point B : D_VB = s . v_B

- Conservation du débit volumique d’un fluide incompressible :

- D_VA = S . v_A = D_VB = s . v_B

- Ainsi :

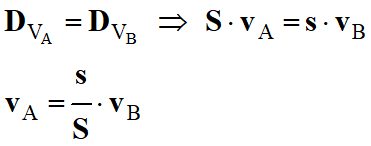
- Comme s << S, alors

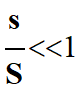
- v_A ≈ 0 m . s^–1

► Relation de Bernoulli :

Relation de Bernoulli

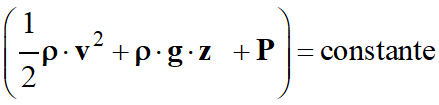
ρ : masse volumique du fluide (kg . m^–3 )

P : pression du fluide au point considéré (Pa)

v : vitesse du fluide au point considéré (m . s^–1)

g : intensité de la pesanteur :

g = 9,81 N. kg^–1 ou g = 9,81 m. s^–2

z : altitude au point considéré (m)

Constante : (J . m^–3)

- Remarque :

- La relation de Bernoulli est constituée de deux termes :

- Le terme : ρ . g . z + P

- Ce terme traduit la pression statique.

- Il est lié à la relation fondamentale de la statique des fluides.

- Le terme :

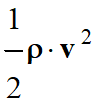
- Ce terme traduit la pression dynamique.

- Il est lié à la force pressante qui s’applique sur un corps maintenu immobile dans un écoulement de fluide à la vitesse v.

- Ce terme permet de tenir compte des corrections à apporter à la loi fondamentale de la statique des fluides lorsque le fluide étudié n’est plus au repos.

► La relation de Bernoulli :

- Elle relie en toute position du fluide d’une même ligne de courant :

- La pression P ;

- La valeur de la vitesse v ;

- La coordonnée verticale z de la position.

- Pour une même ligne de courant :

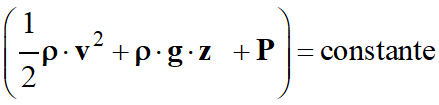
- Relation de Bernoulli

- La relation de Bernoulli appliquée au schéma suivant :

réservoir et légende

- Au point A :

- point A

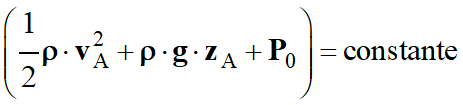
- Comme v_A ≈ 0 m . s^–1

- (ρ . g . z_A + P₀ ≈ constante)

- Au point B :

- point B

- En conséquence :

- Application numérique :

- vB = 4,4 m / s

II- Exercice : Trompe à eau.

1)- Énoncé.

En travaux pratiques, on utilise une pompe à eau lors d'un séchage sur Büchner.

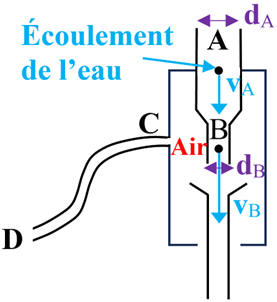
Le dispositif est représenté ci-dessous.

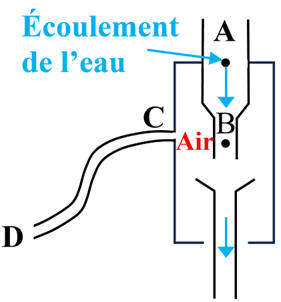
Trompe à eau

Le rétrécissement du tube où circule l'eau provoque une dépression qui aspire l'air à travers l'ouverture C.

Le diamètre de la conduite vaut d_A = 12 mm en A et d_B = 5,0 mm en B.

La distance AB = 5,0 cm est assez faible pour que les effets de la gravité soient négligeables.

DONNÉES :

Masse volumique : ρ_eau = 1000 kg . m^–3

Intensité de la pesanteur g = 9,81 N . kg^–1

a)- Nommer l’effet qui relie l'apparition d'une différence de pression à une variation de vitesse.

b)- Exprimer puis calculer la dépression P_A – P_B en fonction du débit volumique D_V de l'eau, pour D_V = 6,0 L . min^–1.

2)- Correction.

a)- Effet Venturi : différence de pression et variation de vitesse.

► Écoulement d’un fluide dans un tube dont la section diminue :

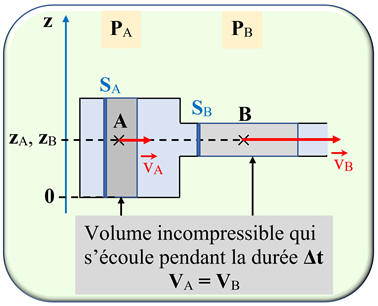
- Schéma de la situation :

Écoulement d’un fluide dans un tube dont la section diminue

- On applique la relation de Bernoulli à l’écoulement d’un fluide incompressible dans un tube qui se resserre.

- La section de la surface S se resserre : S_A > S_B

- Comme le fluide est incompressible et que l’écoulement s’effectue en régime permanent indépendant du temps, le débit volumique est conservé :

- D_V = D_VA = D_VB

- Les deux points A et B sont à la même altitude :

- z_A = z_B

- On applique la relation de Bernoulli à cette situation :

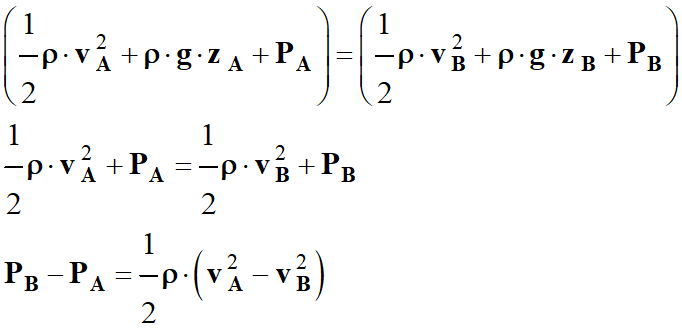
- relation de Bernoulli

- À la lecture de cette relation, on peut en déduire que :

- v_B > v_A => P_B < P_A

- Une valeur de la vitesse en B supérieure à la valeur de la vitesse en A, entraîne une pression plus petite en B qu’en A :

- C’est l’effet Venturi.

b)- Expression et calcul la dépression P_A – P_B en fonction du débit volumique D_V de l'eau.

- Donnée : D_V = 6,0 L . min^–1

- Équation de continuité :

- Conservation du débit volumique :

- S_A . v_A = S_B . v_B

- En utilisant les diamètres d_A et d_B :

- Relation de Bernoulli aux points A et B :

- Relation de Bernoulli

- On considère que les effets de la gravité sont négligeables :

- ρ_eau . g . (z_A – z_B) ≈ 0

- En conséquence :

- En faisant intervenir les données de l’exercice :

trompe à vide

- Les différents diamètres et le débit volumique :

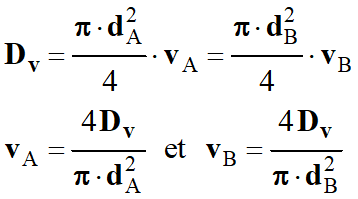
- vA et vB

- Expression de la différence de pression entre P_A et P_B :

- PA - PB

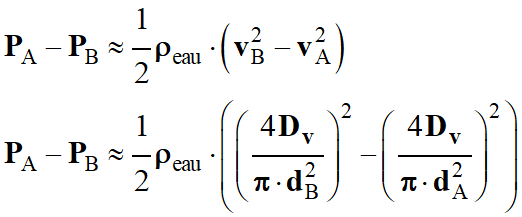
- On développe, on réduit et on factorise :

- PA - PB

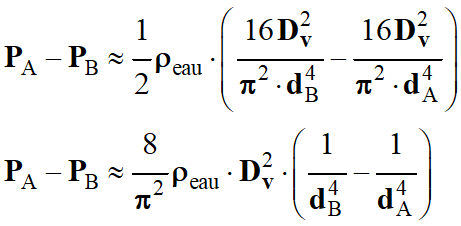
- Application numérique :

- Attention : D_V = 6,0 L . min^–1

- D_V = 1,0 × 10^–4 m^–3 . s^–1

- PA - PB = 1,3 E4 Pa

- Au niveau de la mer, la pression atmosphérique moyenne est d’environ 1013 hPa (hectopascal), ce qui équivaut à 1 atm ou 1 bar.

- 1 bar = 10⁵ Pa

- Dans le cas présent, la dépression est de l’ordre de 130 hPa, soit 0,13 bar environ.

- Cette dépression crée une aspiration au point C, et ainsi au point D.

- La trompe à eau permet de réaliser des filtrations rapides de solutions comportant une phase solide.

Filtration sur filtre Büchner

Filtration sous filtre Büchner

Fabrication d'un savon de Marseille

III- Exercice : Tube de Venturi.

1)- Énoncé.

Sur un tube de Venturi, un tube en U contenant du mercure Hg est branché entre deux positions 1 et 2.

De l'eau traverse le tube avec un débit volumique D_V.

Dans la direction perpendiculaire à l'écoulement horizontal de l'eau dans le tube, les fluides sont statiques.

Schéma :

DONNÉES :

Masses volumiques : ρ_Hg = 13550 kg . m^–3 ; ρ_eau = 1000 kg . m^–3

Intensité de la pesanteur g = 9,81 N . kg^–1

Diamètres des sections : d₁ = 10 mm ; d₂ = 5,0 mm

Hauteur h = 0,30 m

a)- Exprimer puis calculer la différence de pression entre les deux positions 1 et 2 en fonction de la différence de niveau h, puis en fonction du débit volumique du fluide D_V.

b)- Exprimer puis calculer le débit volumique D_V du fluide en fonction de la différence de niveau h mesurée dans le tube en U.

2)- Correction.

a)- Expression et calcul de la différence de pression entre les 2 positions 1 et 2 en fonction de la différence de niveau h, puis en fonction du débit volumique du fluide D_V.

- Schéma :

- Relation de Bernoulli appliquée aux points 1 et 2 :

- Relation de Bernoulli

- Avec z₁ = z₂ = 0

- Relation de Bernoulli

- Maintenant, considérons les points A₁ et A₂ , situés sur une ligne de courant infiniment proche de la partie inférieure du tube de Venturi.

- Relation de Bernoulli appliquée aux points A₁ et A₂ :

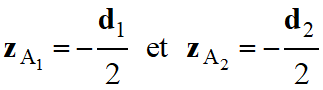
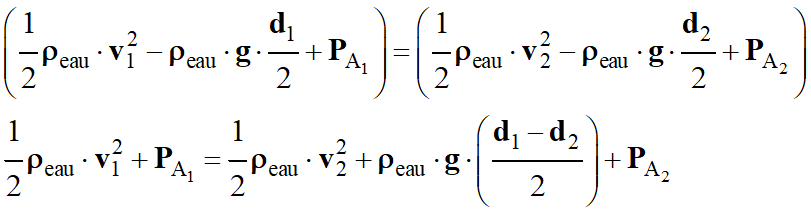
- Relation de Bernoulli

- Avec :

- Relation de Bernoulli

- On tire l’expression suivante :

- expression PA1 - PA2

► La partie statique :

- Dans la direction perpendiculaire à l'écoulement horizontal de l'eau dans le tube, les fluides sont statiques.

- Loi fondamentale de la statique des fluides :

- Relation :

P_B – P_A = ρ . g . ( z_A – z_B)

P : pression en pascal (Pa)

ρ : masse volumique du fluide au repos (kg . m^–3)

g : intensité de la pesanteur (N . kg^–1)

z : coordonnée verticale (m)

L’axe des coordonnées verticales est orienté vers le haut

- Schéma :

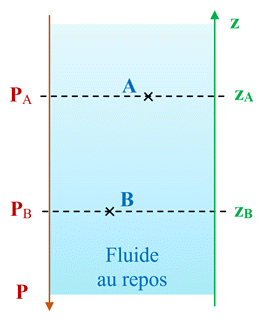
pression et profondeur

- Considérons les points A₁ et B₁ :

- P_B1 – P_A1 = ρ_eau . g . ( z_A1 – z_B1)

- P_B1 – P_A1 = ρ_eau . g . A₁B₁

- Considérons les points A₂ et B₂ :

- P_B2 – P_A2 = ρ_eau . g . ( z_A2 – z_B2)

- P_B2 – P_A2 = ρ_eau . g . A₂B₂

- Différence de pression entre les points B₁ et B₂ :

- P_B1 = P_A1 + ρ_eau . g . A₁B₁ et P_B2 = P_A2 + ρ_eau . g . A₂B₂

- P_B1 – P_B2 = P_A1– P_A2 + ρ_eau . g . (A₁B₁ – A₂B₂)

- Étude de l’expression (A₁B₁ – A₂B₂)

- Il faut relier cette expression à la grandeur h :

- L’étude du schéma permet d’écrire la relation suivante :

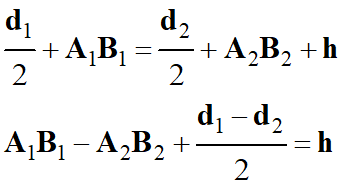
- relation

- Et :

- PA1 - PA2

- En conséquence :

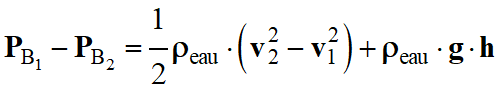
- Du point de vue du mercure, on peut écrire la relation suivante :

- P_B₁ – P_B2 = ρ_Hg . g . h

- Différence de pression entre P₁ et P₂ :

- P1 - P2

- Or :

- P1 - P2

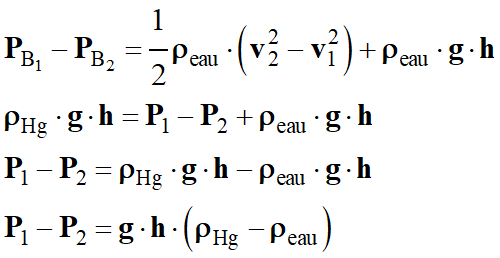
- Application numérique :

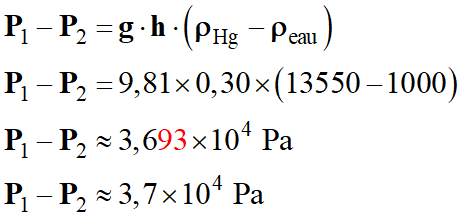
- P1 - P2 = 3,7 E4 Pa

b)- Expression et calcul du débit volumique D_V du fluide en fonction de la différence de niveau h mesurée dans le tube en U.

- L’équation de continuité permet d’écrire la relation suivante :

- S₁ . v₁ = S₂ . v₂

- En utilisant les diamètres d₁ et d₂ :

- v1 et v2

- D’autre part :

- P_B₁ – P_B2 = ρ_Hg . g . h

- et :

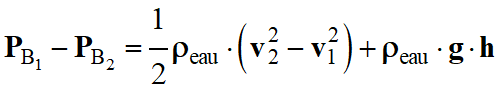
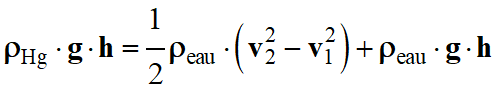
- En utilisant les expressions de v₁ et v₂ en fonction de D_v

- expression

- On va exprimer D_v en fonction des autres paramètres :

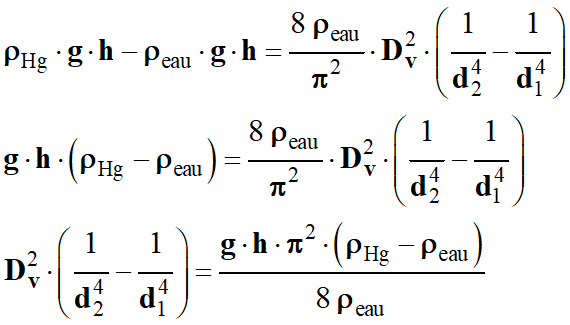
- Dv au carré

- Et enfin :

- Application numérique :

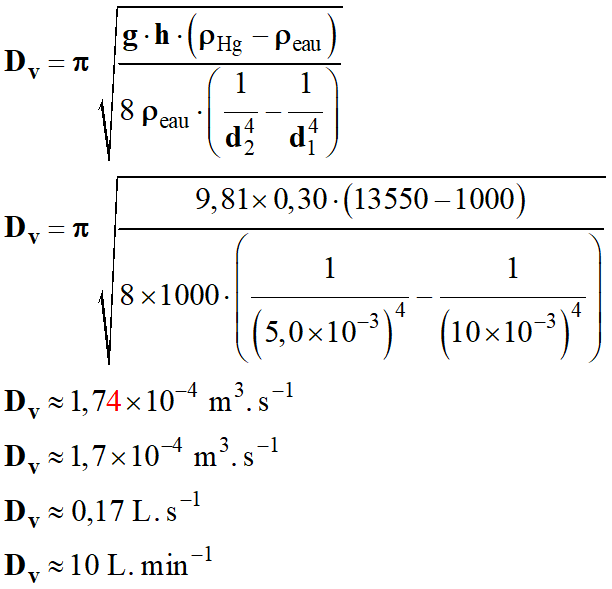
- Dv = 0,17 L / s ou 10 L / min

IV- Exercice : Siphon.

1)- Énoncé.

Pour vider partiellement un réservoir parallélépipédique contenant de l'eau, on utilise un siphon qui est un tube de section d'aire constante s.

Note Ʃ l'aire de la section du réservoir.

Soient A le point d'entrée du siphon, B le point le plus haut du siphon, C un point à la sortie du siphon et D un point de la surface libre dans le réservoir.

La surface libre dans le réservoir et l'extrémité C du siphon sont à la pression atmosphérique Pa.

L'origine des ordonnées est prise au fond du réservoir.

réservoir et siphon

DONNÉES :

z_A = 5,0 cm ; z_B = 70 cm ; z_C = – 10 cm ; à l’instant initial : z_D = 60 cm.

Intensité de la pesanteur g = 9,81 N . kg^–1

ρ_eau = 1000 kg . m^–3

Pa = 1013 hPa

Ʃ = 1,0 m².

s = 1,0 cm²

a)- En considérant s << Ʃ, comparer les vitesses d'écoulement de l'eau au point D et au point C.

b)- Calculer la vitesse d'écoulement de l'eau à la sortie du siphon. En déduire une condition pour que le fluide s'écoule.

c)- Calculer les pressions P_A et P_B dans l'eau aux points A et B.

d)- En déduire ce qu'il faut faire pour amorcer le siphon. La hauteur du point B peut-elle être quelconque ?

2)- Correction.

a)- Comparaison des vitesses d'écoulement de l'eau au point D et au point C.

- On considère que : s << Ʃ

- Schéma :

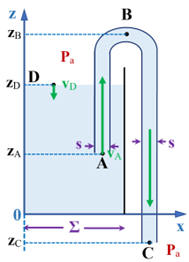
réservoir et siphon

- Équation de continuité :

- Conservation du débit volumique : aux points D et A

- s . v_A = Ʃ . v_D

- D’autre part :

- Conservation du débit volumique : aux points A et C

- s . v_A = s . v_C

- Conséquence :

- s . v_C = Ʃ . v_D

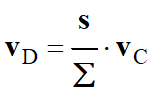
- Comme s << Ʃ, alors

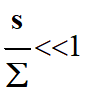
- v_D ≈ 0 m . s^–1

b)- Vitesse d'écoulement de l'eau à la sortie du siphon.

- Schéma :

réservoir et siphon

- Relation de Bernoulli appliquée entre les points C et D :

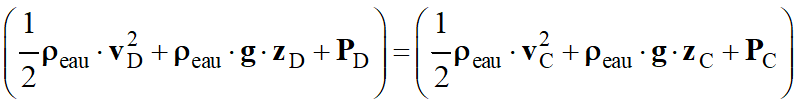
- relation de Bernoulli

- Or v_D ≈ 0 m . s^–1 et P_D = P_a = P_C

- Condition pour que le fluide s'écoule :

- Pour que le fluide s’écoule, il faut que z_D > z_C.

- Vitesse d’écoulement de l’eau au point C :

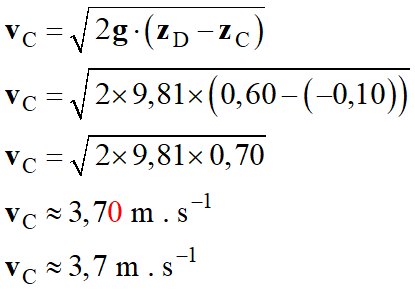
- vC = 3,7 m / s

c)- Valeurs des pressions P_A et P_B dans l'eau aux points A et B.

- Relation de Bernoulli appliquée entre les points A et B :

- Relation de Bernoulli

- Conservation du débit volumique : aux points A et B

- s . v_A = s . v_B = s . v_C

- Conséquence :

- Relation de Bernoulli appliquée entre les points C et B :

- Relation de Bernoulli

- Conservation du débit volumique : aux points A et B

- s . v_A = s . v_B = s . v_C

- et P_a = P_C

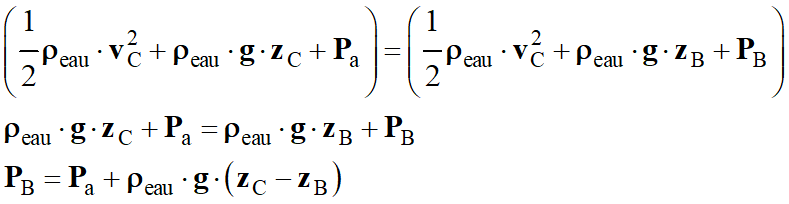
- Valeur de la pression au point B (à l’état initial):

- P_B = P_a + ρ_eau . g . (z_C – z_B)

- P_B = 1,013 × 10⁵ + 10000×9,81 × ( – 0,10 – 0,70)

- P_B ≈ 9,34 × 10⁴ Pa

- P_B ≈ 9,3 × 10⁴ Pa

- Valeur de la pression au point A (à l’état initial):

- P_A = P_B + ρ_eau . g . (z_B – z_A)

- P_A = P_a + ρ_eau . g . (z_C – z_B) + ρ_eau . g . (z_B – z_A)

- P_A = P_a + ρ_eau . g . (z_C – z_A)

- Application numérique :

- P_A = P_a + ρ_eau . g . (z_C – z_A)

- P_A = 1,013 × 10⁵ + 10000×9,81 × ( – 0,10 – 0,050)

- P_A ≈ 9,98 × 10⁴ Pa

- P_A ≈ 1,0 × 10⁵ Pa

d)- Amorçage du siphon.

- Retour sur l’expression de la pression au point B :

- P_B = P_a + ρ_eau . g . (z_C - z_B)

- Pour que le siphon fonctionne, il faut que la valeur de la pression au point B soit positive.

- Il faut que le point D soit au-dessus du point C et que le point B soit au-dessus du point D.

- On peut écrire la relation précédente sous une autre forme :

- P_B = P_a + ρ_eau . g . (z_C – z_B)

- P_B = P_a – ρ_eau . g . (z_B – z_C)

- zB - zC

- Application numérique :

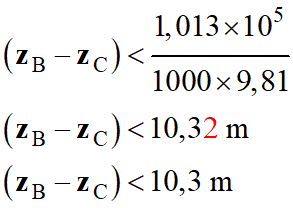
- zB - zC < 10,3 m

- C'est la même valeur que celle de la hauteur maximale pour une colonne d'eau trouvée par Torricelli.

- La hauteur du point B ne peut être quelconque.

- Pour amorcer un siphon, il faut suivre ces étapes générales :

- Remplir le siphon de liquide, soit avant la mise en place, soit par un amorçage qui consiste à créer une dépression (par aspiration) pour permettre au liquide du réservoir de s'engager dans le tuyau.

- Placer l'extrémité d'entrée du siphon dans le récipient supérieur contenant le liquide.

- Amorcer le siphon en aspirant doucement sur l'extrémité d'entrée pour créer une dépression et faire entrer le liquide dans le siphon.

- Une fois que le liquide commence à couler, il est important de maintenir la pression pour éviter que de l'air n'intervienne et ne désamorce le siphon.

- Il est également essentiel de vérifier que l'extrémité de sortie du siphon est à un niveau inférieur au niveau du réservoir pour que le mouvement se poursuive.

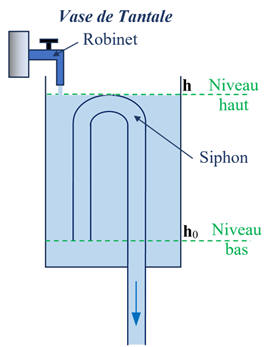
► Vase de Tantale :

Vase de Tantale

vase de Tantale