|
|
Sens d'évolution spontanée d'un système chimique Exercices |
|
|
|
|
|
QCM r La transformation non totale. L’évolution spontanée d’un système Le transfert spontanée d’électrons.
|
1)- Exercice 05 page 144 : Déterminer un taux d’avancement final :
|
Déterminer un taux d’avancement final : Un fil de cuivre Cu (s) de masse m (Cu) = 5,0 g est plongé dans une solution de volume V = 100 mL contenant des ions argent telle que [Ag+] = 0,075 mol. La solution se colore en bleu et un dépôt d’argent se forme sur le cuivre. L’absorbance de la solution, à λ = 500 nm, est
égale à 0,47. Courbe : 1.
Écrire l’équation de la réaction. 2.
À l’aide du taux d’avancement, conclure au
caractère total ou non de la transformation.
-
Données :
-
Ag+ (aq) /
Ag (s) ;
Cu2+
(aq) / Cu (s)
-
M (Cu)
= 63,5 g . mol–1 |
|
Déterminer un taux d’avancement final : 1.
Équation de la réaction.
-
Réactifs :
-
Un fil de cuivre
Cu (s)
-
les ions argent
Ag+(aq)
-
Produits :
-
La solution se colore en bleu :ceci
est dû à la formation des ions
Cu2+ (aq)
-
Dépôt d’argent
Ag (s)
-
Au cours de la réaction
d’oxydoréduction :
-
Le cuivre métal
Cu (s) a été oxydé en ions cuivre II,
Cu2+ (aq) Cu (s)
→ Cu 2+
(aq)
+ 2
e –
-
L’ion argent
Ag+(aq) a été réduit en argent métal,
Ag (s) Ag + (aq)
+
e
– →
Ag (s)
-
Équation de la réaction :
2.
Taux d’avancement.
-
Quantités de matière des réactifs :
-
Quantité de matière initiale de
cuivre métal Cu (s)
-
Quantité de matière initiale d’ions
argent Ag +
(aq)
-
Tableau d’avancement :
-
Il faut déterminer les valeurs de
l’avancement maximal, xmax
et de l’avancement final, xf.
-
On peut déterminer la valeur de
l’avancement final à partir de la connaissance
de la quantité de
matière d’ions cuivre II,
Cu 2+
(aq), formés.
-
Par exploitation graphique à partir
de la valeur de l’absorbance de la solution obtenue,
on peut déduire
la valeur de la concentration en ions cuivre II, [Cu 2+].
-
Exploitation graphique :
A = 0,47
-
Les mesures :
-
Valeur de la concentration en
Cu2+
(aq) de la solution :
-
[Cu 2+] ≈ 3,7 × 10–2
mol . L–1
-
Quantité de matière finale en
Cu
2+
(aq)
-
n (Cu2+)
= [Cu
2+] .
V
-
n (Cu2+)
≈ 3,7 × 10–2 × 100 × 10–
3
-
n (Cu2+)
≈ 3,7 × 10–3 mol
-
Valeur de l’avancement finale de la
réaction :
-
D’après le tableau d’avancement :
-
xf =
n (Cu2+) ≈ 3,7 × 10–3 mol
-
Valeur de l’avancement maximal.
-
On remarque que le cuivre métal est
en excès par rapport aux ions argent :
-
ni (Ag+) ≈ 7,5 mmol et ni (Cu)
≈ 79 mmol
-
ni (Cu) ≈ 10 ni (Ag+)
-
L’ion argent
Ag+ (aq) est le réactif limitant :
-
ni (Ag+) – 2
xmax
= 0
-
-
Taux d’avancement final de la
réaction :
-
Le taux d’avancement final d’une
réaction, noté τ (tau),
est le quotient
de l’avancement final par l’avancement maximal :
-
-
τ ≈ 0,97 ≈ 1, la réaction est
quasi-totale. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2)- Exercice 07 page 145 : Exprimer un quotient de réaction :
|
Exprimer un quotient de réaction : Soient les équations des réactions suivantes :
1.
Exprimer les quotients de réaction Qr1 et
Qr2 associés
aux équations (1) et (2). 2.
L’expression du quotient de réaction
dépend-elle de l’écriture de l’équation de réaction ? |
|
Exprimer un quotient de réaction : 1.
Expression des quotients de réaction Qr1 et
Qr2 associés
aux équations (1) et (2).
-
L’espèce solide
PbO (s) n’intervient pas dans le quotient de réaction.
-
De même, l’eau est aussi le solvant
et n’intervient pas dans le quotient de la réaction :
2.
L’expression
du quotient de réaction et écriture de l’équation de réaction :
-
L’expression du quotient de réaction
Qr est liée à
l’écriture de l’équation de la réaction chimique.
-
Dans le cas présent on remarque :
-
L’équation de la
réaction (2) est l’équation de la
réaction (1) multipliée par deux.
-
On remarque que :
-
Qr2 =
(Qr1)2
-
Il ne faut pas oublier que le
quotient de réaction est
une grandeur sans unité
qui caractérise un système chimique dans un état donné.
-
Dans cet exercice, on a utilisé
l’expression simplifiée du quotient de réaction
Qr.
-
On n’a pas fait intervenir la
concentration standard : C0 = 1,0 mol . L–1
|
||||||||||||||||||||||||||||
3)- Exercice 09 page 145 : Prévoir un sens d’évolution spontanée :
|
Prévoir un sens d’évolution spontanée : À un volume V = 20 mL d’une solution de nitrate de plomb
II telle que [Pb2+]
= 1,0 × 10–2 mol . L–1 est ajouté, sans
variation de volume à 25 ° C, 200 mg de poudre d’étain Sn (s). À l’état final, [Sn2+]f
= 2,5 × 10–3 mol . L–1. À 25 ° C, la constante d’équilibre K associée à
l’équation de la réaction est égale à 0,33. 1.
Écrire l’équation de la réaction modélisant
la transformation. 2.
Calculer la valeur du quotient de réaction à
l’état initial du système considéré. 3.
En déduire le sens d’évolution spontanée du
système. 4.
Calculer la valeur du quotient de réaction à
l’état final du système. Conclure.
-
Données :
-
Couples : Pb2+ (aq)
/ Pb (s) ; Sn2+ (aq) / Sn (s)
-
M (Sn)
= 118,7 g . mol–1. |
Prévoir un sens d’évolution spontanée : 1.
Équation de la réaction modélisant la
transformation.
-
Réactifs :
-
Solution de nitrate de plomb II :
Pb2+ (aq) + 2
NO3– (aq)
-
Les ions nitrate sont des ions
spectateurs.
-
L’étain en poudre :
Sn (s)
-
Produits :
-
À partir des couples donnés :
-
Plomb à l’état solide : Pb
(s)
-
Et des ions étain II : Sn2+
(aq)
-
Il s’agit d’une réaction
d’oxydoréduction :
Sens direct
Pb2+
(aq)
+
Sn
(s)
Pb
(s)
+
Sn2+
(aq)
Sens
inverse
2.
Valeur du quotient de réaction à l’état
initial Qr,i du système considéré.
-
Quotient de réaction simplifié à
l’état initial Qr,i
du système :
-
-
Au départ :
-
[Pb2+]i
= 1,0 × 10–2 mol . L–1
-
[Sn2+]i
= 0,0 mol . L–1
-
En conséquence :
-
Qr,i ≈ 0 3.
Sens d’évolution spontanée du système.
-
Qr,i ≈ 0
-
K = 0,33
Sens direct
Pb2+
(aq)
+
Sn
(s)
Pb
(s)
+
Sn2+
(aq) 4.
Valeur du quotient de réaction à l’état
final Qr,f du système.
-
-
[Sn2+]f
= 2,5 × 10–3 mol . L–1
-
Il faut déterminer la valeur de la
concentration en ions plomb II Pb2+ (aq) à l’état
final :
-
Quantités de matière :
-
Quantité de matière initiale d’étain
métal Sn (s) Masse
m
(Sn) = 200 mg
Masse
molaire
M
(Sn) = 118,7 g . mol–1
-
Quantité de matière initiale d’ions
plomb II Pb2+
(aq)
Volume
V
= 20 mL
Concentration
[Pb2+]i = 1,0 × 10–2 mol . L–1
ni
(Pb2+) =
[Pb2+]i
×
V
ni
(Pb2+) ≈
1,0 × 10–2 × 20 × 10– 3
ni
(Pb2+) ≈
2,0 × 10–
4 mol
ni
(Pb2+) ≈
0,20 mmol
-
On remarque que l’étain à l’état
solide Sn (s) est en excès.
-
Le réactif limitant est l’ion plomb
II : Pb2+
(aq)
-
Tableau d’avancement de la réaction : Équation
Pb2+
(aq)
+
Sn (s
Pb (s)
+
Sn2+ (aq)
État
Avancement
x
(mol)
État
initial
(mmol)
0
ni (Pb2+)
≈
0,20
ni (Sn)
≈
1,68
0
0
État
Intermédiaire
(mmol)
x
ni (Pb2+)
– x
ni (Sn) – x
x
x
État
final
(mmol)
xf
ni (Pb2+)
– xf
ni (Sn) – xf
xf
xf
État
maximal
(mmol)
xmax
ni (Pb2+)
– xmax
= 0
ni (Sn) – xmax
xmax
xmax
-
ni (Pb2+)
– xmax = 0 => xmax
= ni (Pb2+)
≈ 0,20 mmol
-
xmax = ni
(Pb2+)
≈ 2,0 × 10–
4 mol
-
Détermination de l’avancement final :
xf
-
D’après le tableau d’avancement :
-
xf = ni
(Sn2+)
-
xf = [Sn2+]f
× V
-
xf = 2,5 × 10–3
× 20 × 10–3
-
xf ≈ 5,0 × 10–5
mol
-
On remarque que
xf < xmax
-
On peut calculer le taux d’avancement
final de la réaction :
-
-
La réaction est non totale.
-
Quotient de réaction à l’état final :
-
nf (Pb2+)
= ni
(Pb2+)
– xf
-
nf (Pb2+)
≈ 2,0 ×
10–
4 –
5,0 × 10–5
-
nf (Pb2+)
≈ 1,5 × 10–
4 mol
-
-
Conclusion :
-
Qr,f =
K =
Qr,éq
-
À l’état final, le système a atteint
son état d’équilibre.
-
Tableau d’avancement Équation
Pb2+
(aq)
+
Sn (s
Pb (s)
+
Sn2+ (aq)
État
Avancement
x
(mol)
État
initial
(mmol)
0
ni (Pb2+)
≈ 0,20
ni (Sn) ≈ 1,68
0
0
État
Intermédiaire
(mmol)
x
ni (Pb2+)
– x
ni (Sn) – x
x
x
État
final
(mmol)
xf
0,15
1,63
0,050
0,050
État
maximal
(mmol)
xmax
0
1,48
0,20
0,20
![]()
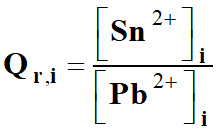

![]()
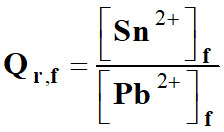
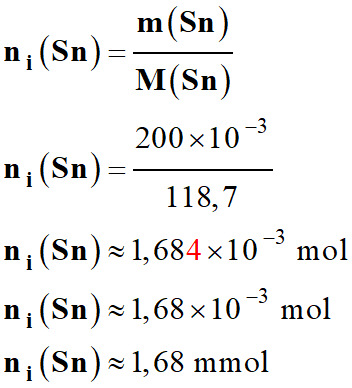
![]()
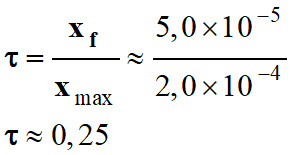
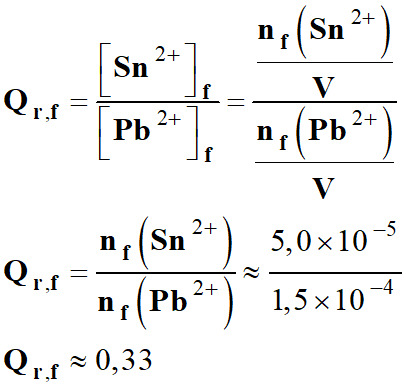
![]()
![]()
4)- Exercice 10 page 145 : Évaluer une constante d’équilibre :
|
Évaluer une constante d’équilibre : À 25 ° C, dans une fiole jaugée de 250,0 mL, sont dissous
totalement une masse m1= 1,21 g de nitrate de fer III
nonahydraté {Fe(NO3)3, 9 H2O}
(s), une masse m2 = 0,870 g de sulfate de fer II
heptahydraté {FeSO4, 7 H2O}
(s), une masse m3 = 0,640 g de nitrate d’argent
AgNO3 (s) et de la poudre d’argent Ag (s) est ajoutée. On complète au trait de jauge avec de l’eau distillée. La transformation est modélisée par deux réactions opposées.
L’équation s’écrit :
1.
Calculer le quotient de réaction à l’état
initial Qr,i. 2.
Sachant que la masse d’argent diminue,
comparer la constante d’équilibre K, à 25 ° C, au quotient de
réaction à l’état initial. 3.
À 25 ° C, dans un erlenmeyer, sont ajoutées
les solutions suivantes :
-
De l’argent
Ag (s) se forme.
Déterminer un encadrement de la constante d’équilibre
K.
-
Données :
-
M
(Fe(NO3)3)
= 241,9 g . mol–1 ;
M
(FeSO4)
= 151,9 g . mol–1
-
M
(AgNO3) = 169,9 g . mol–1 ;
M (H2O) = 18,0 g . mol–1 |
Évaluer une constante d’équilibre : 1.
Valeur du quotient de réaction à l’état
initial Qr,i.
-
Réaction chimique :
Fe3+ (aq)
+
Ag
(s)
Fe2+
(aq)
+
Ag+
(aq)
-
-
Préparation de la solution :
-
On dissout une masse
m1= 1,21 g de nitrate de fer III nonahydraté {Fe(NO3)3,
9 H2O} (s)
-
Équation de dissolution : la
dissolution est totale.
Eau
Fe(NO3)3,
9 H2O (s)
→
Fe3+
(aq)
+
3
NO3– (aq)
n1 = ni
(Fe3+)
3 n1
= ni
(NO3–)
-
On
dissout une masse m2
= 0,870 g de sulfate de fer II heptahydraté {FeSO4,
7 H2O} (s),
-
Équation de dissolution :
Eau
FeSO4,
7 H2O (s)
→
Fe2+
(aq)
+
SO42–
(aq)
n2 = ni
(Fe2+)
n2 =
ni (SO42–)
-
On dissout une masse m3
= 0,640 g de nitrate d’argent AgNO3 (s)
-
Équation de dissolution :
Eau
AgNO3
(s)
→
Ag+
(aq)
+
NO3–
(aq)
n3 = ni
(Ag+)
n3 = ni
(NO3–)
-
Les ions nitrate et sulfate sont des
ions spectateurs, ils ne participent pas à la réaction.
-
Concentration des différentes
espèces :
-
Concentration en ions fer III, Fe3+
(aq) Masse
m1
= 1,21 g
Masse
molaire M
(Fe(NO3)3,
9 H2O (s))
= 403,9 g . mol–1
Volume :
V
=
250,0 mL
-
Concentration en ions fer II, Fe2+
(aq) Masse
m2
= 0 ,870 g
Masse
molaire M
(FeSO4,
7 H2O)
= 277,9 g . mol–1
Volume :
V
=
250,0 mL
-
Concentration en ions Argent, Ag+
(aq) Masse
m3
= 0,640 g
Masse
molaire M
(AgNO3)
= 169,9 g . mol–1
Volume :
V
=
250,0 mL
-
Concentration des différentes espèces
pour le mélange 1 :
Mélange
1
Solutions
Fe3+ (aq)
Fe2+ (aq)
Ag+ (aq)
C
(mol . L–1)
1,20
× 10–2
1,25
× 10–2
1,51
× 10–2
-
Valeur du quotient de
réaction initial, Qr,i
:
-
2.
Comparaison de K et Qr,i.
-
Équation de la réaction :
Sens direct
Fe3+
(aq)
+
Ag
(s)
Fe2+
(aq)
+
Ag+
(aq)
Sens inverse
-
Lorsque les espèces chimiques sont
mises en présence :
-
Les ions fer III, Fe3+
(aq), les ions fer II, Fe2+
(aq), les ions argent Ag+
(aq)
-
et l’argent métal
Ag (s)
-
On indique que la masse d’argent
solide Ag (s) diminue.
-
On en déduit que la réaction évolue
dans le sens direct :
-
Et que Qr,i
<
K
=> K >
1,57 × 10–2 3.
Détermination de l’encadrement de la
constante d’équilibre K :
-
Lors du mélange, il y a une
augmentation du volume.
Mélange 2
Solutions
Fe3+ (aq) + 3 NO3– (aq)
Fe2+ (aq) + SO42– (aq)
Ag+ (aq) + NO3– (aq)
C
(mol . L–1)
C1
= 1,0 × 10–4
C2
= 5,0 × 10–2
C2
= 1,0 × 10–2
V
(mL)
V1
= 30,0
V2
= 50,0
V3
= 20,0
-
Volume de la solution obtenue :
-
Vsol =
V1 +
V2 +
V3
-
Vsol = 30,0 +
50,0 + 20,0
-
Vsol ≈ 100 mL
-
Concentration des différentes
espèces :
-
Concentration en ions fer III, Fe3+
(aq)
-
-
Concentration en ions fer II, Fe2+
(aq)
-
-
Concentration en ions argent
Ag+ (aq)
-
-
Concentration des différentes espèces
du mélange 2 :
Mélange
2
Solutions
Fe3+ (aq)
Fe2+ (aq)
Ag+ (aq)
C
(mol . L–1)
3,0 ×
10–5
2,5 ×
10–2
2,0 ×
10–3
-
Équation de la réaction :
Sens direct
Fe3+
(aq)
+
Ag
(s)
Fe2+
(aq)
+
Ag+
(aq)
Sens
inverse
-
On indique que lors du mélange des
trois solutions, de l’argent
métal se forme.
-
La réaction s’effectue dans le sens
inverse :
-
Dans ce cas,
Qr,i
>
K
-
Valeur du quotient de
réaction dans ce cas :
-
-
Qr,i >
K => K < 1,7
-
Or, on a vu que K
> 1,57 × 10–2 1,57 × 10–2
< K < 1,7
►
Additif :
-
On étudie toujours la réaction
suivante :
Sens direct
→
Fe3+
(aq)
+
Ag
(s)
Fe2+
(aq)
+
Ag+
(aq)
Sens
inverse
←
-
Quotient de réaction déduit de cette
écriture :
-
-
Relation de Nernst :
-
Couple
Ox /
Red :
Ox
+
n
e–
Red
Ox
+
n
e–
E
Potentiel
d'oxydoréduction du couple Ox / Red (V)
E0
Potentiel standard du couple Ox / Red :
n
Nombre d’électrons échangés.
[Ox]
Concentration de l’oxydant (mol . L–1)
[Red]
Concentration du réducteur conjugué (mol . L–1)
-
On fait intervenir les concentrations
des espèces chimiques en remplacement des
activités.
-
Exemple :
-
Pour le couple
Fe3+ (aq) / Fe2+ (aq)
: E10
= 0,77 V :
Fe3+ (aq)
+
1
e–
Fe2+ (aq)
-
-
Pour le couple
Ag+ (aq) / Ag
(s) : E20
= 0,80 V
Ag+ (aq)
+
1
e–
Ag (s)
-
Potentiel d’oxydoréduction :
-
-
Ag (s) est une espèce solide :
son activité est égale à
1.
-
Retour sur la réaction en utilisant
la relation de Nernst et
les potentiels standard d’oxydoréduction :
-
Pour le couple
Fe3+ (aq) / Fe2+ (aq)
: E10
= 0,77 V
-
Pour le couple
Ag+ (aq) / Ag (s)
: E20
= 0,80 V
-
Dans les conditions standard :
-
À l’aide des potentiels standard, on
peut prévoir le sens d’évolution d’une réaction dans les conditions
standard.
-
Dans le cas présent, on fait
intervenir les couples Ag+
(aq) / Ag (s) et
Fe3+ (aq) / Fe2+ (aq) :
-
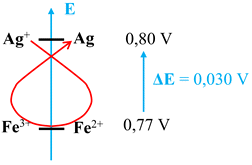
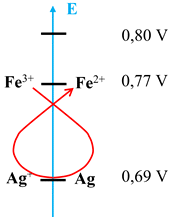
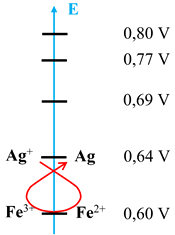
Règle du gamma :
-
On place les couples
Ox
/ Red sur une échelle par
potentiel décroissant.
-
L’oxydant le plus fort (ici
Ag+ (aq) ) réagit avec le réducteur le plus fort (Fe2+
(aq)).
-
Expression de
ΔE :
-
Sens direct
Fe3+
(aq)
+
Ag
(s)
Fe2+
(aq)
+
Ag+
(aq)
Sens inverse
←
-
La réaction évolue spontanément dans le sens
inverse de l'écriture de la réaction.
-
On peut calculer la constante
d’équilibre de cette réaction à partir de la valeur de la tension.
-
À l’équilibre chimique
ΔE = 0.
-
Qr =
Qr,éq =
K
-
-
Conclusion :
Sens direct
→
K ≈ 0,31
Fe3+
(aq)
+
Ag
(s)
Fe2+
(aq)
+
Ag+
(aq)
Sens
inverse
←
-
L’équilibre est déplacé dans le sens
inverse de l’écriture de la réaction.
-
La réaction est non totale (K << 104). On est en présence d’un équilibre chimique.
►
Retour sur le mélange 1 :
-
Dans l’énoncé, il est indiqué que de
la quantité d’argent métallique
diminue.
-
La réaction évolue donc dans le sens
direct de l’écriture de la réaction.
-
Comment expliquer ce phénomène ?
-
On connait les différentes
concentrations des espèces présentes dans l’état initial du
système :
-
Concentration des différentes espèces
pour le mélange 1 :
Mélange
1
Solutions
Fe3+ (aq)
Fe2+ (aq)
Ag+ (aq)
C
(mol . L–1)
1,20
× 10–2
1,25
× 10–2
1,51
× 10–2
-
On n’est pas dans les conditions
standard pour les concentrations.
-
On calcule le potentiel
d’oxydoréduction de chaque couple à l’état initial :
-
Couple
Ag+ (aq) /
Ag (s) :
-
-
Couple
Fe3+ (aq) /
Fe2+ (aq) :
-
-
En conséquence
E1 > E2 :
-
Avec les concentrations initiales, la
réaction évolue bien dans le sens direct de l’écriture de la
réaction :
Sens direct
→
K ≈ 0,31
Fe3+
(aq)
+
Ag
(s)
Fe2+
(aq)
+
Ag+
(aq)
-
Elle s’arrête lorsque l’état
d’équilibre est atteint.
►
Retour sur le mélange 2 :
-
Dans l’énoncé, il est indiqué que de
la quantité d’argent métallique
augmente.
-
La réaction évolue donc dans le inverse de l’écriture de la réaction.
-
Comment expliquer ce phénomène ?
-
On connait les différentes
concentrations des espèces présentes dans l’état initial du
système :
-
Concentration des différentes espèces
pour le mélange 2 :
Mélange
2
Solutions
Fe3+ (aq)
Fe2+ (aq)
Ag+ (aq)
C
(mol . L–1)
3,0 ×
10–5
2,5 ×
10–2
2,0 ×
10–3
-
On n’est pas dans les conditions
standard pour les concentrations.
-
On calcule le potentiel
d’oxydoréduction de chaque couple à l’état initial :
-
Couple
Ag+ (aq) /
Ag (s) :
-
-
Couple
Fe3+ (aq) /
Fe2+ (aq) :
-
-
En conséquence
E1 < E2 :
-
Avec les concentrations initiales, la
réaction évolue bien dans le sens inverse de l’écriture de la
réaction :
Fe3+ (aq)
+
Ag
(s)
Fe2+
(aq)
+
Ag+
(aq)
Sens
inverse
←
-
Elle s’arrête lorsque l’état
d’équilibre est atteint.

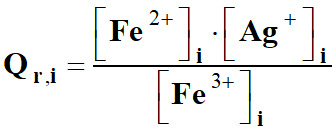
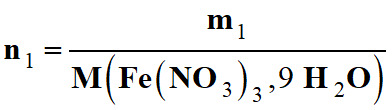
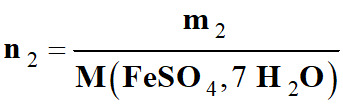
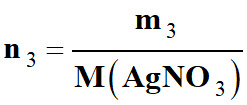


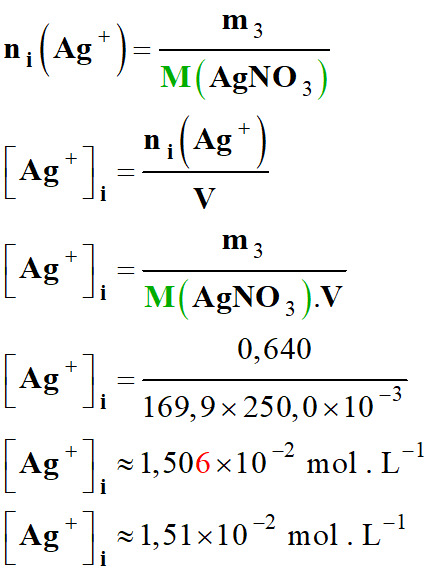
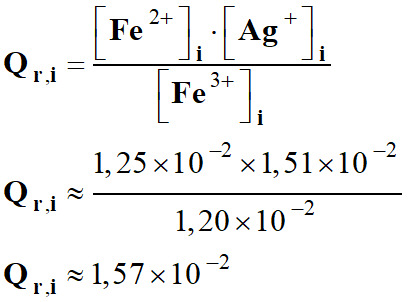
![]()


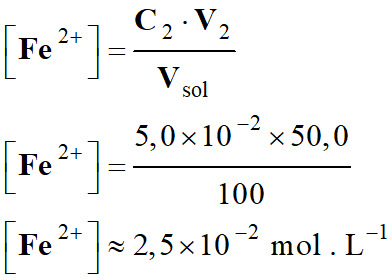
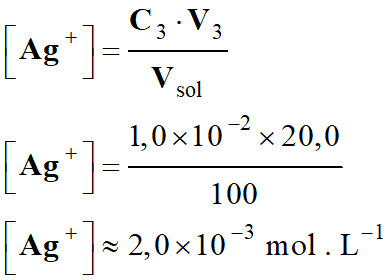
![]()

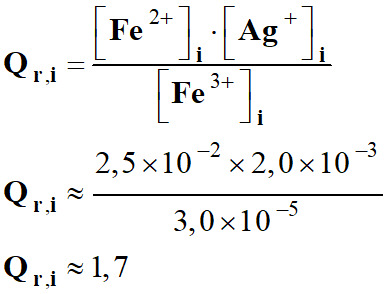
![]()
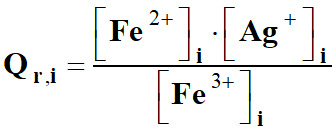
![]()
 Red
Red
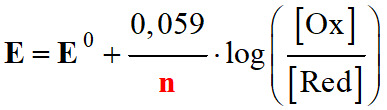

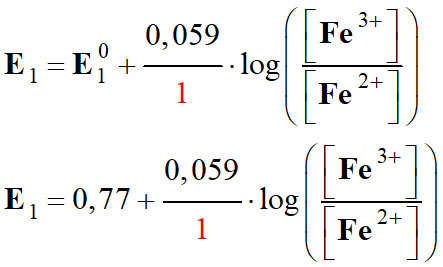

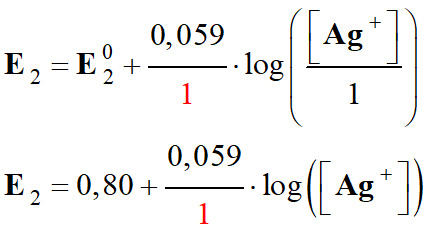
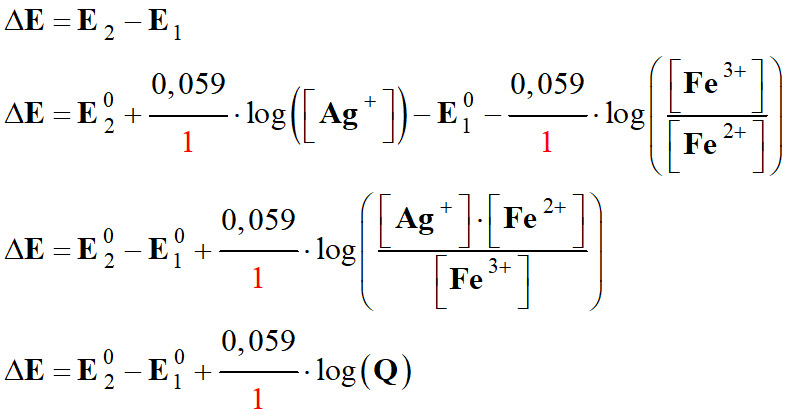
![]()
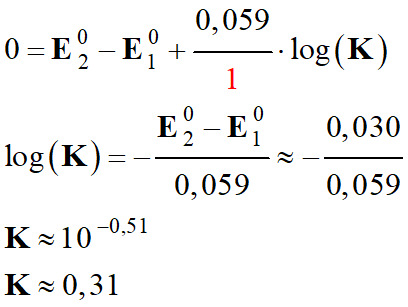
![]()
![]()
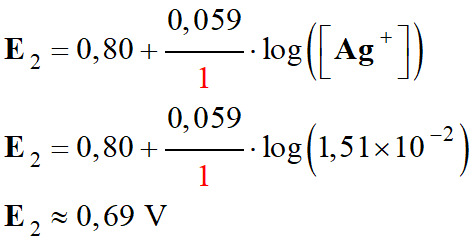

![]()
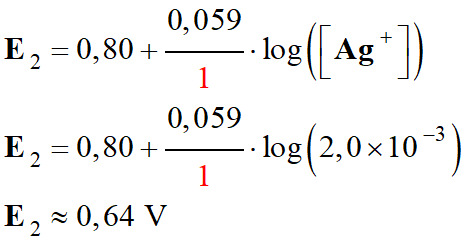

![]()
![]()
![]()
5)- Exercice 13 page 146 : Identifier la polarité d’une pile :
|
Identifier la polarité d’une pile : Une pile met en jeu les couples Cd2+ (aq) / Cd (s) et Ag+ (aq) / Ag (s) permet d’actionner une petite hélice. La tension mesurée est
négative si la borne COM du voltmètre est reliée à
l’électrode d’argent. 1.
Schématiser le montage et préciser les
bornes de la pile. 2.
En déduire l’équation de la réaction de
fonctionnement de la pile. 3.
Déterminer si le transfert d’électrons est
direct ou indirect. |
|
Identifier la polarité d’une pile : Les couples Cd2+ (aq) / Cd (s) et Ag+
(aq) / Ag (s). La tension mesurée est négative si la borne COM du
voltmètre est reliée à l’électrode d’argent. 1.
Schéma du montage de la pile.
-
La tension mesurée est négative
lorsque la borne COM du voltmètre est reliée à l’électrode d’argent.
-
L’électrode d’argent constitue la
borne positive et l’électrode de cadmium la
borne négative. 2.
Équation de la réaction de fonctionnement de
la pile.
-
Dans le cas présent,
l’électrode d’argent constitue la
borne positive de la pile et
l’électrode de cadmium la
borne négative.
-
Le courant, généré par cette pile,
circule de l’électrode d’argent vers l’électrode de cadmium à
l’extérieur de la pile. - Les électrons, responsables du passage de ce courant dans le circuit électrique (fils et électrodes),
circulent de l’électrode de cadmium vers l’électrode
d’argent à l’extérieur du circuit.
-
À l’intérieur de la pile les porteurs
de charges sont les ions. - Le courant électrique à l’intérieur de la pile est dû à la double migration des ions positifs et négatifs, présents dans les différentes solutions, se déplaçant en
sens inverses.
►
Réactions aux électrodes. - Les électrons, responsables du passage du courant dans le circuit électrique (fils et électrodes), circulent de l’électrode de cadmium vers l’électrode d’argent à
l’extérieur du circuit.
-
Les électrons qui partent de
l’électrode de cadmium sont libérés par la réaction suivante : Cd (s)
→ Cd2+ (aq)
+ 2
e
–
-
Les électrons qui arrivent à
l’électrode d’argent sont consommés par la réaction suivante : Ag+ (aq)
+
e
– →
Ag (s)
►
Polarité de la pile et nom des
électrodes.
-
À la
borne positive, ici
l’électrode d’argent, les électrons qui arrivent sont consommés par
la réaction Ag + (aq)
+
e
– →
Ag (s)
-
Cette électrode est appelée la
Cathode.
-
L’argent métal Ag
(s) est formé.
-
À la
borne négative de la
pile, ici l’électrode de cadmium les électrons sont créés par la
réaction Cd (s)
→ Cd2+ (aq)
+ 2
e
–
-
Cette électrode est appelée l’anode.
-
Le cuivre métal Cd
(s) est
consommé.
►
Équation de la réaction :
-
On est en présence d’un générateur
électrochimique qui transforme de l’énergie chimique en énergie
électrique. 3.
Transfert d’électrons est direct ou
indirect.
-
Il s’est produit un échange
d’électrons de façon indirecte par l’intermédiaire du circuit
électrique entre l’électrode de cadmium et l’électrode d’argent.
-
Le pont salin :
-
Relie les deux demi-piles.
-
Permet de fermer le circuit pour
assurer la circulation du courant.
-
Assure la neutralité électrique des
solutions.
-
Le pont salin contient généralement
une solution aqueuse ionique gélifiée. |
6)- Exercice 17 page 146 : Identifier des oxydants et des réducteurs :
|
Identifier des oxydants et des réducteurs : 1.
Les ions hypochlorite CℓO–
(aq) contenus dans l’eau de Javel sont-ils oxydants ou réducteurs ? 2.
Citer un oxydant usuel ne contenant pas
l’élément chlore. |
|
Identifier des oxydants et des réducteurs : 1.
Les ions hypochlorite CℓO–
(aq) contenus dans l’eau de Javel :
-
L’eau de Javel est une
solution aqueuse.
-
Son pouvoir désinfectant
dépend de la valeur de sa concentration en ions hypochlorite.
-
Lorsque celle-ci passe
au-dessous d’une certaine valeur, l’eau de Javel n’est plus
efficace.
-
Les bidons d’eau de Javel
indiquent une date limite d’utilisation.
-
L’ion hypochlorite
CℓO– (aq) est un oxydant.
-
Son réducteur conjugué est
l’ion chlorure
Cℓ– (aq)
-
Couple oxydant / réducteur :
-
Demi-équation électronique :
► Rappel :
Ox + n e–
►
Eau de Javel en « berlingot ».
-
Les indications du fabricant sur le
berlingot sont les suivantes :
-
Volume : 250 mL ;
-
Degré chlorométrique : 48 ° ; ou
Chlore actif
►
Composition :
-
Solution aqueuse d’hypochlorite de
sodium ( Na+
(aq) + ClO–
(aq)) et de chlorure de sodium ;
-
L’eau de Javel est obtenue par
réaction entre le dichlore et la soude :
-
L’eau de Javel est une solution
aqueuse contenant des ions
ClO–, Na+
et Cl– en milieu basique.
-
L’ion hypochlorite
ClO– confère à la solution un caractère oxydant mais cet
ion possède aussi les caractères d’une base
-
L’eau de Javel se décompose lentement
selon la réaction d’oxydoréduction suivante :
►
Bidon d’eau de Javel :
-
Tableau :
- Berlingot : - Pictogramme de danger :
-
Lorsqu’on verse de l’acide
chlorhydrique concentré dans 100 mL de solution d’eau de Javel, il
se produit la réaction d’équation : Cℓ–
(aq) +
CℓO–
(aq) + 2 H+ (aq) →
Cℓ2
(g) + H2O (ℓ)
-
La masse de chlore actif
indiqué sur l’étiquette correspond à la masse de dichlore libéré au
cours de cette transformation pour 100 g de solution.
- Ainsi, une eau de Javel
à 2,6 % de chlore actif
libère 2,6 g de dichlore au cours de cette transformation
pour 100 g de solution.
-
Le dichlore est un gaz toxique qu’il faut
absolument éviter de respirer.
2.
Oxydant usuel ne contenant pas l’élément
chlore.
►
Les oxydants :
-
Un bon
oxydant : Espèce chimique
capable de capter
facilement des électrons.
-
Tableau des espèces oxydantes à
connaître :
►
Couple
MnO4–
(aq) / Mn2+
(aq) :
-
L’ion permanganate est un
oxydant en milieu acide.
►
L’eau oxygénée :
-
L’eau oxygénée
H2O2
(aq) est l’oxydant du couple:
H2O2
(aq) / H2O (ℓ).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7)- Exercice 21 page 147 : La pluie d’or :
|
La pluie d’or : Les ions iodure I– (aq) et les ions plomb II,
Pb2+ (aq) réagissent pour former de l’iodure de
plomb PbI2 (s). La transformation est modélisée par deux réactions opposées. L’équation s’écrit : Pb2+ (aq) + 2 I–
(aq)
À 25 ° C, la constante
d’équilibre est K (25 ° C) = 7,4 × 107. On dissout totalement dans l’eau distillée : une masse m1 = 5,0 g d’iodure de potassium
KI (s) et une masse m2 = 5,0 g de nitrate de plomb II
Pb(NO3)2 (s). Le volume de la solution est V = 50 ,0 mL. 1.
Déterminer s’il se forme des cristaux
d’iodure de plomb PbI2 (s). 2.
Lorsque le système n’évolue plus :
-
[Pb2+]final
= 1,5 × 10–3 mol . L–1 et
-
[I–]final
= 3,0 × 10–3 mol . L–1
-
Calculer le taux d’avancement de la
réaction et le quotient de réaction
Qr,A à l’état
final A.
-
Conclure 3.
Le mélange réactionnel (décrit en 2.) est
alors plongé dans un bain-marie thermostaté à 70 ° C (état B). a.
Indiquer la valeur du quotient de réaction
Qr,B avant toute nouvelle transformation. b.
La solution devient limpide. D’après cette
observation, à 70 ° C, comparer Qr,B à la
constante d’équilibre K de cette
réaction. c.
En déduire l’influence de la température sur
la constante d’équilibre K de cette réaction. 4. La solution limpide est refroidie dans un bain de glace. Quand la solution change d’aspect, après agitation, une « pluie d’or » apparaît. Proposer une explication à la formation des
cristaux d’iodure de plomb PbI2
(s). 5. La solution est ensuite filtrée. Une pointe de spatule de nitrate de plomb est ajoutée au filtrat. À l’aide du quotient de
réaction, discuter du sens d’évolution du système.
-
Données :
-
M (Pb(NO3)2)
= 331 g . mol–1.
-
M (KI)
= 166 g . mol–1. |
|
La pluie d’or : 1.
Formation des cristaux d’iodure de plomb
PbI2 (s).
-
Préparation de la solution :
-
On dissout totalement dans l’eau
distillée
-
une masse m1 = 5,0
g d’iodure de potassium KI (s) et
-
une masse m2 = 5,0
g de nitrate de plomb II Pb(NO3)2
(s).
-
Le volume de la solution est V
= 50 ,0 mL.
►
Préparation de la solution :
-
Équation de dissolution : la
dissolution est totale.
-
On dissout une masse
m1 = 5,0 g d’iodure de potassium KI (s)
-
On
dissout une masse m2
= 5,0 g de nitrate de plomb II Pb(NO3)2
(s),
-
Équation de dissolution :
-
Concentration des différents ions
présents dans la solution :
-
Concentration des ions iodure :
-
[I–]
= [K+] ≈ 0,60
mol . L–1
-
Concentration des ions plomb II :
Pb2+
(aq)
-
[Pb2+]
≈ 0,30 mol . L–1 et [NO3–]
= 2 [Pb2+] ≈
0,60 mol . L–1
-
Équation de la réaction : Pb2+ (aq) + 2 I–
(aq)
-
Les ions potassium
K+ (aq) et les ions nitrate
NO3– (aq) sont des ions spectateurs.
-
Quotient de réaction :
-
-
Quotient de la réaction à l’état
initial :
-
Réactifs :
-
Pb2+ (aq) et
I– (aq)
-
Produit :
-
PbI2 (s)
-
-
Or
K (25 ° C) = 7,4 × 107
-
La réaction évolue dans le sens
direct de l’écriture de la réaction.
-
Il se forme des cristaux d’iodure de
plomb II, PbI2
(s) jaune.
-
K (25 ° C) > 104,
la réaction est quasi-totale :
xf =
xmax
-
Tableau d’avancement de la réaction :
-
Valeur de l’avancement maximal :
xmax
-
Comme, on est en présence de deux
réactifs, on peut émettre deux hypothèses.
-
Hypothèse 1 : On considère que
le réactif limitant est Pb2+
(aq) :
-
15
– xmax1 = 0 =>
xmax1 = 15 mmol
-
Hypothèse 2 : On considère que
le réactif limitant est l’ion
I– (aq) :
-
30 –
2 xmax2
=> xmax2 = 15 mmol
-
Les réactifs sont dans
les proportions stœchiométriques :
-
xmax
= xmax1
= xmax2
2.
Taux d’avancement de la réaction et le
quotient de réaction Qr,A à l’état final A
:
-
Tableau d’avancement de la réaction :
-
[Pb2+]final
= 1,5 × 10–3 mol . L–1 et
-
[I–]final
= 3,0 × 10–3 mol . L–1
-
Conclusion :
-
Valeur de l’avancement maximal :
xmax = 15 mmol
-
Valeur de l’avancement final :
xf
-
En fin de réaction :
-
[Pb2+]final
= 1,5 × 10–3 mol . L–1 et
-
nf (Pb2+) =
[Pb2+]final
. V
-
nf (Pb2+) ≈
1,5 × 10–3 × 50,0 × 10–3
-
nf (Pb2+) ≈
7,5 × 10–5 mol
-
nf (Pb2+) ≈
0,075 mmol
-
De même :
-
[I–]final
= 3,0 × 10–3 mol . L–1
-
nf (I–) =
[I–]final
. V
-
nf (I–) ≈
3,0 × 10–3 × 50,0 × 10–3
-
nf (I–) ≈
1,5 × 10–4 mol
-
nf (I–) ≈
0,15 mmol
-
Par rapport à l’ion plomb II :
-
15
–
xf ≈
0,075
-
xf
≈ 14,9 mmol
-
De même :
-
30 –
2 xf ≈ 0,15
-
xf ≈ 14,9 mmol
-
Taux d’avancement de la réaction :
-
Le taux d’avancement final d’une
réaction, noté τ (tau),
est le quotient de
l’avancement final par l’avancement maximal :
-
- La réaction est quasi-totale. - Ce
résultat est bien en accord avec la valeur de la constante
d’équilibre K à 25 ° C.
-
Valeur du quotient de réaction
Qr,A à l’état
final A :
-
-
Qr,f
=
Qr,A ≈ 7,4 ×
107 3.
Le mélange réactionnel dans l’état B
: bain-marie thermostaté à 70 ° C. a.
Valeur du quotient de réaction Qr,B
avant toute nouvelle transformation.
-
Avant toute nouvelle transformation :
-
Rien ne change : Qr,B
,= Qr,A ≈ 7,4
× 107 b.
Comparaison de Qr,B à la
constante d’équilibre K de cette réaction.
-
La solution devient limpide. Le
précipité jaune d’iodure de plomb II disparaît.
-
La système évolue dans le sens
inverse de l’écriture de la réaction chimique :
-
D’après cette observation, à 70 ° C :
c.
Influence de la température sur la constante
d’équilibre K de cette réaction.
-
Dans le cas présent, une
augmentation de la température entraîne la
diminution de la valeur de la constante d’équilibre de la réaction.
-
Le précipité jaune disparaît. 4.
Explication à la formation des cristaux
d’iodure de plomb PbI2 (s).
-
Lorsque la température diminue, la
constante d’équilibre de la augmente.
-
Lorsqu’elle est supérieure au
quotient de réaction, le système évolue dans le
sens direct de l’écriture de la
réaction.
-
Il se forme alors de l’iodure de
plomb II jaune PbI2
(s). 5.
Sens d’évolution du système.
-
La solution est ensuite filtrée.
-
Lorsque le système n’évolue plus :
-
[Pb2+]final
= 1,5 × 10–3 mol . L–1 et
-
[I–]final
= 3,0 × 10–3 mol . L–1
-
Après filtration, on peut considérer
que les concentrations en ions plomb II Pb2+ (aq) et ions iodure I–
(aq) n’ont pas changées.
-
Avant l’ajout de nitrate de plomb :
-
-
Qr,f
=
Qr,A =
K ≈ 7,4 × 107
-
Une pointe de spatule de nitrate de
plomb { Pb(NO3)2 (s)} est ajoutée au filtrat entraîne une
augmentation de la concentration en ions plomb II, Pb2+
(aq).
-
La concentration [Pb2+] augmente, alors le quotient de réaction initial
Qr,i
diminue.
-
Qr,i <
K
-
En conséquence, le système évolue
dans le sens direct de l’écriture de
la réaction.
-
Il se forme alors de l’iodure de
plomb II jaune, PbI2
(s). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
8)- Exercice 26 page 149 : Des piles « rechargeables » :
|
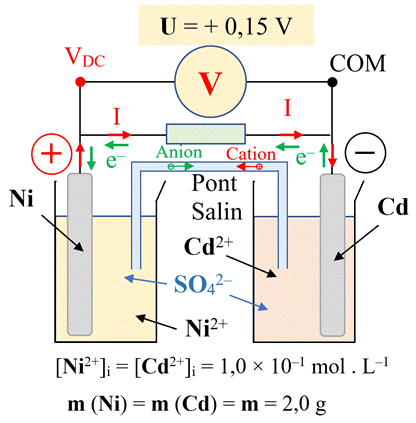
Des piles « rechargeables » : Le recyclage des piles est difficile. L’utilisation de piles
« rechargeables » semble une alternative plus écologique. La pile nickel-cadmium, « rechargeable », est constituée de deux demi-piles reliées par un pont salin et mettant en jeu les couples oxydant / réducteur Ni2+ (aq) / Ni (s) et
Cd2+ (aq) / Cd (s). La première demi-pile contient 20,0 mL de solution gélifiée de
sulfate de nickel telle que [Ni2+] = 1,0 × 10–1
mol . L–1. L’autre demi-pile contient une solution de sulfate de cadmium
telle que [Cd2+]i = [Ni2+]i. Chacune des deux électrodes a une masse initiale m = 2,0
g. En branchant la borne COM d’un voltmètre à l’électrode de
cadmium Cd, la tension mesurée est U =+ 0,15 V 1.
Écrire l’équation de la réaction de
fonctionnement de la pile. 2.
Donner l’expression du quotient de réaction
Qr,i à l’état initial, puis le calculer
numériquement. 3. Sachant qu’à 25 ° C, la constante d’équilibre associée à l’équation de la réaction est K = 4,5
× 106, prévoir le sens d’évolution spontané du système
chimique constituant la pile. 4. Faire un schéma de la pile et indiquer le sens de circulation des électrons. Le transfert spontané d’électrons
est-il direct ou indirect ? 5.
Indiquer le rôle du pont salin et justifier
la nécessité de séparer les réactifs dans deux demi-piles. 6.
Calculer la capacité électrique Qmax
de la pile Ni-Cd. 7.
La plupart des équipements électroniques
nomades actuels sont équipés de batteries rechargeables lithium-ion. a.
Le dioxygène gazeux intervient dans la pile.
Cette espèce est-elle réductrice ou oxydante ? b.
La configuration électronique d’un atome de
lithium est 1s2 2s1. Justifier
le caractère réducteur du métal lithium. 8. La capacité d’une pile de téléphone portable est de 4320 C. Sachant que le lithium est le réactif limitant, déterminer la masse de lithium contenu dans une pile lithium-ion.
-
Données :
-
Couple oxydant / réducteur :
Li+ (aq) /
Li (s)
-
NA = 6,02 × 1023
mol–1 et e = 1,60 × 10–19 C
-
M (Ni)
= 58,7 g . mol–1 ;
M (Cd) = 112,4 g .
mol–1
-
M (Li)
= 6,94 g . mol–1
|
Des piles « rechargeables » :
-
Pile Ni-Cd : 1.
Équation de la réaction de fonctionnement de
la pile.
-
La tension mesurée est positive
lorsque la borne COM du voltmètre est reliée à l’électrode de
cadmium.
-
L’électrode de nickel constitue la
borne positive et l’électrode de cadmium la borne négative.
-
Électrode positive :
-
Dans le cas présent,
l’électrode de nickel constitue la
borne positive de la pile et
l’électrode de cadmium la
borne négative.
-
Le courant, généré par cette pile,
circule de l’électrode de nickel vers l’électrode de cadmium à
l’extérieur de la pile.
-
Les électrons, responsables du
passage de ce courant dans le circuit électrique (fils et
électrodes),
circulent de l’électrode de cadmium vers l’électrode de
nickel à l’extérieur du circuit.
-
À l’intérieur de la pile les porteurs
de charges sont les ions.
-
Le courant électrique à l’intérieur
de la pile est dû à la double migration des ions positifs et
négatifs, présents dans les différentes solutions, se déplaçant en
sens inverses.
►
Réactions aux électrodes.
-
Les électrons, responsables du
passage du courant dans le circuit électrique (fils et électrodes),
circulent de l’électrode de cadmium vers l’électrode d’argent à
l’extérieur du circuit.
-
Les électrons qui partent de
l’électrode de cadmium sont libérés par la réaction suivante : Cd (s)
→ Cd2+ (aq)
+ 2
e
–
-
Il se produit une oxydation à
l’anode.
-
Les électrons qui arrivent à
l’électrode de nickel sont consommés par la réaction suivante : Ni2+ (aq)
+
2 e
– →
Ag (s)
-
Il se produit une réduction à la
cathode.
►
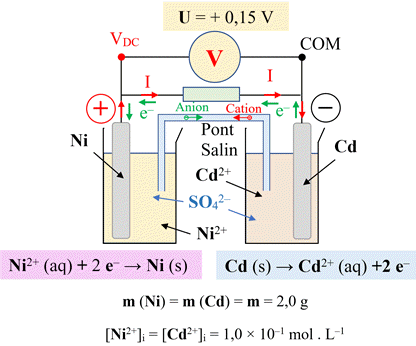
Équation de la réaction :
Ni2+
(aq)
+
2
e
– →
Ni
(s)
Cd
(s)
→
Cd2+
(aq)
+
2
e
–
Ni2+
(aq) +
Cd
(s)
→
Ni
(s)
+
Cd2+
(aq)
-
On est en présence d’un générateur
électrochimique qui transforme de l’énergie chimique en énergie
électrique. 2.
Quotient de réaction Qr,i
à l’état initial.
-
-
Avec [Ni2+]i
= [Cd2+]i = 1,0 × 10–1 mol .
L–1
-
3.
Sens d’évolution spontané du système
chimique constituant la pile.
-
À 25 ° C, la constante d’équilibre
associée à l’équation de la réaction
-
K
= 4,5 × 106,
-
En conséquence :
Qr,i < K
Sens direct
Ni2+
(aq)
+
Cd
(s)
Ni
(s)
+
Cd2+
(aq) 4.
Schéma de la pile :
-
Les électrons circulent dans le
circuit électrique de l’électrode de cadmium vers l’électrode de
nickel (dans le circuit électrique).
-
Le transfert spontané d’électrons est
indirect Il se fait par
l’intermédiaire du circuit électrique. 5.
Rôle du pont salin.
-
Le pont salin :
-
Relie les deux demi-piles.
-
Permet de fermer le circuit pour
assurer la circulation du courant.
-
Assure la neutralité électrique des
solutions.
-
Permet de séparer les réactifs.
-
La séparation des réactifs permet de
faire en sorte que le transfert des électrons, au lieu d’être direct entre les réactifs, soit indirect. 6.
Capacité électrique Qmax
de la pile Ni-Cd.
-
Schéma de la pile :
-
Quantités de matière de réactifs :
-
Quantité de matière d’ions nickel II,
Ni2+
(aq) :
Volume
V
= 20,0 mL
Concentration [Ni2+]i = 1,0 × 10–2 mol . L–1
ni
(Ni2+) =
[Ni2+]i
× V
ni
(Ni2+) ≈
1,0 × 10–2 × 20,0 × 10– 3
ni
(Ni2+) ≈
2,0 × 10–
4 mol
ni
(Ni2+) ≈
0,20 mmol
-
Quantité de matière de cadmium
solide : Masse
m
(Cd) = 2,0 g
Masse
molaire
M
(Cd) = 112,4 g . mol–1
-
Tableau d’avancement de la réaction : Équation
Ni2+ (aq)
+
Cd (s)
Ni
(s)
+ Cd2+ (aq)
État
Avancement
n
(Ni2+)
n
(Cd)
n
(Ni)
n
(Cd2+)
État
initial
(mmol)
0
ni
(Ni2+) ≈
0,20
ni
(Cd) ≈ 18
ni
(Ni)
ni
(Cd2+)
État
Intermédiaire
(mmol
x
ni
(Ni2+) –
x
ni
(Cd) – x
ni
(Ni) + x
ni
(Cd2+) +
x
État
final
(mmol)
xf
ni
(Ni2+) –
xf
ni
(Cd) – xf
ni
(Ni) + xf
ni
(Cd2+) +
xf
État
maximal
(mmol)
xmax
ni
(Ni2+) –
xmax
ni
(Cd) – xmax
ni
(Ni) + xmax
ni
(Cd2+) +
xmax
-
On remarque que
ni (Cd)
> ni (Ni2+)
-
En conséquence l’ion nickel II, Ni2+
(aq), est le réactif limitant.
-
ni (Ni2+)
– xmax = 0 =>
xmax ≈ 0,20
mol
-
Remarques :
-
K = 4,5 × 106
> 104
-
La réaction est quasi-totale :
xf ≈
xmax ≈ 0,20 mol
-
Tableau d’avancement : Équation
Ni2+ (aq)
+
Cd (s)
→
Ni
(s)
+ Cd2+ (aq)
État
Avancement
n
(Ni2+)
n
(Cd)
n
(Ni)
n
(Cd2+)
État
initial
(mmol)
0
ni
(Ni2+) ≈
0,20
ni
(Cd) ≈ 18
ni
(Ni)
ni
(Cd2+)
État
Intermédiaire
(mmol
x
ni
(Ni2+) –
x
ni
(Cd) – x
ni
(Ni) + x
ni
(Cd2+) +
x
État
final
(mmol)
xf
= xmax
ni
(Ni2+) –
xf = 0
ni
(Cd) – xf
ni
(Ni) + xf
ni
(Cd2+) +
xf
État
maximal
(mmol)
0,20
0
17,8
ni
(Ni) + 0,20
ni
(Cd2+) +
0,20
-
La capacité électrique d’une pile est
la charge électrique maximale
Qmax que la pile peut débiter durant sa durée de vie. Qmax
= n (e–)max . NA
. e
Qmax
Capacité électrique de la pile (coulomb : C)
n
(e–)max
Quantité maximale d’électrons échangés (mol)
NA
Nombre d’Avogadro (mol–1)
NA
= 6,02 × 1023 mol–1
e
Charge élémentaire (coulomb : C)
e = 1,60 ×
10–19 C
-
Il faut déterminer la valeur de n
(e–)max.
-
Il faut utiliser la demi-équation
électronique relative aux ions nickel II,
Ni2+, (réactif
limitant) faisant intervenir les électrons :
Ni2+
(aq) +
2 e– →
Ni
(s)
-
En conséquence :
n (e–)max
= 2 xmax
-
Qmax =
n (e–)max .
NA .
e
-
Qmax = 2
xmax .
NA . e
-
Qmax = 2 ×
0,20 × 6,02 × 1023 × 1,60 × 10–19
(mol . mol–1 . C)
-
Qmax ≈ 3,85
× 104 C
-
Qmax ≈ 3,9 ×
104 C 7.
Batteries rechargeables lithium-ion. a.
Le dioxygène gazeux :
-
L’oxygène
O2 (g)
-
Cette l’espèce oxydante du couple
O2 (g) /
H2O (ℓ) Ox
+
n
e
–
Red
½ O2
(g)
+
2 H+
(aq) + 2 e–
H2O (ℓ) b.
Caractère réducteur du métal lithium.
-
Configuration électronique d’un atome
de lithium : 1s2
2s1.
-
Il appartient à la première colonne
de la classification périodique.
-
Il a tendance à céder un électron
pour obtenir la configuration électronique du gaz rare qui le
précède (l’hélium : He).
-
C’est le réducteur du couple
Li+ (aq) /
Li (s). Ox
+
n
e –
Red
Li+
(aq)
+
e–
Li (s) 8.
Masse de
lithium contenu dans une pile lithium-ion.
-
La capacité d’une pile de téléphone
portable : Qmax
= 4320 C.
-
Le lithium est le réactif limitant :
-
xmax = ni
(Li)
-
Or :
-
-
D’autre part :
-
n (e–)max
= xmax
-
-
Capacité électrique de la pile :
-
Qmax =
n (e–)max .
NA .
e
-
Qmax =
xmax .
NA . e
-
Application numérique :
-
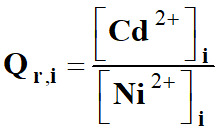
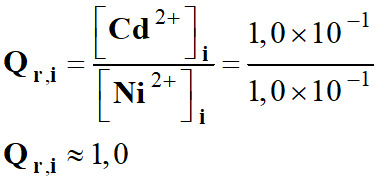




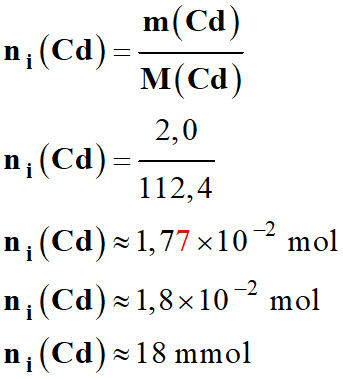
![]()
![]()
![]()
![]()
![]()
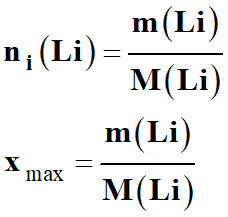

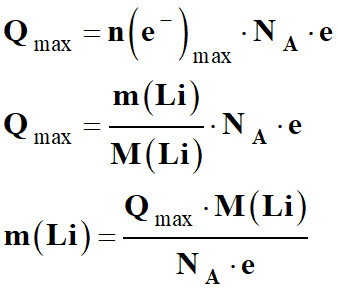
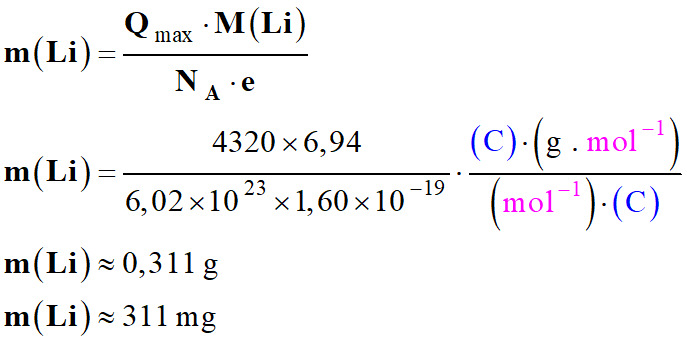
|
|