|
|
Interactions, Forces et Champs Exercices |
|
|
|
|
1)- Exercice 03 page 184 : Exprimer la force de gravitation :
|
Exprimer la force de gravitation :
Sa masse est : MJ = 1,90 × 1027 kg.
-
Exprimer la force exercée par le
Soleil sur Jupiter puis calculer sa valeur.
-
Données :
-
Masse du Soleil : MS
= 1,99 × 1030 kg.
-
Masse de Jupiter : MJ
= 1,90 × 1027 kg.
-
Distance Soleil-Jupiter : dSJ
= 7,79 × 108 km |
|
Exprimer la force de gravitation :
-
Masse de Jupiter : MJ
= 1,90 × 1027 kg.
-
Distance Soleil-Jupiter : dSJ
= 7,79 × 108 km
-
G
est appelé la constante de gravitation universelle :
-
G
≈ 6,67 × 10–11 m3 . kg–1 . s–2
ou m2 . kg–2 . N
-
Expression vectorielle de la force
exercée par le Soleil sur Jupiter :
-
Schéma :
-
-
Expression de la force exercée par le
Soleil sur Jupiter :
-
-
Valeur de la force exercée par le
Soleil sur Jupiter :
- - Jupiter et ses satellites :
|
2)- Exercice 07 page 184 : Comparer des interactions :
|
Comparer des interactions : La Lune et la Terre sont en interaction gravitationnelle. Les forces de gravitation modélisant cette interaction valent :
Fg = 2,0 ×1020 N. Dans la fluorine, solide ionique de formule chimique CaF2, les cations calcium et les anion fluorure sont en interaction électrostatique.
La force électrostatique modélisant une de ces interactions vaut : Fe = 8,6 ×10–9 N. - Sous forme d’un tableau, présenter les analogies et les
différences entre les deux interactions décrites. |
|
Comparer des interactions : - Analogies et les différences entre l’interaction gravitationnelle et l’interaction électrostatique.
-
Attention : pour la valeur de la
force : les charges sont des grandeurs algébriques.
-
Pour ne pas avoir de problème :
-
il faut écrire :
-
pour l’expression vectorielle :
-
|
3)- Exercice 09 page 185 : Électriser la matière :
|
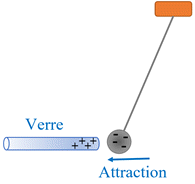
Électriser la matière : On électrise par frottement deux tiges, l’une de verre et l’autre de
polystyrène. On approche ces tiges d’une sphère métallique chargée négativement et suspendue à un fil : Schémas :
1.
Déterminer la charge de l’extrémité de
chaque tige. 2. Expliquer, en considérant les déplacements de charges opérés, comment chaque tige a été électrisée. |
Électriser la matière : 1.
Charge de l’extrémité de chaque tige.
-
Premier cas : Interaction entre la
tige de polystyrène et la sphère métallique :
-
La sphère métallique est chargée
négativement (elle possède un excès d’électrons)
-
Lorsque l’on approche la tige de
polystyrène de la sphère métallique, il y a répulsion.
-
Comme deux charges de mêmes signes se
repoussent, la tige de polystyrène est chargée
négativement.
-
Deuxième cas : Interaction entre la
tige de verre et la sphère métallique :
-
La sphère métallique est chargée
négativement (elle possède un excès d’électrons)
-
Lorsque l’on approche la tige de
verre de la sphère métallique, il y a attraction.
-
Comme deux charges de signes
contraires s’attirent, la tige de verre est chargée
positivement. 2.
Électrisation de chaque tige :
-
Électrisation de la tige de
polystyrène par frottement.
-
La tige de polystyrène arrache des
électrons au chiffon avec lequel elle est frottée.
-
La tige de polystyrène possède à sa
surface un excès d’électrons.
-
Électrisation de la tige de
verre par frottement.
-
Le chiffon avec lequel la tige
de verre est frottée arrache des électrons à la surface de celle-ci.
-
La tige de verre possède ainsi un
défaut d’électrons : elle est chargée positivement.
-
Ce type d’expériences permet de mettre en évidence
l’existence de deux types de charge électrique.

![]()
4)- Exercice 10 page 185 : Étudier une migrations des ions :
|
Étudier une migrations des ions : Pour étalonner un conductimètre, on plonge la cellule conductimétrique dans une solution aqueuse contenant des ions potassium K+
et des ions chlorure Cℓ–. L’appareil applique une tension électrique entre les deux plaques de la cellule qui sont alors chargées, l’une positivement, l’autre
négativement. 1.
Identifier la force responsable de la mise
en mouvement des ions entre les plaques. 2.
Migrations : a. Quand les cations potassium migrent vers la plaque de droite, quel est le signe de la charge portée par cette
plaque ? b.
Indiquer comment migrent alors les anions ?
-
Schéma de la cellule
conductimétrique :
|
Étudier une migrations des ions : 1.
Force responsable de la mise en mouvement
des ions entre les plaques.
-
La tension électrique entre les deux
plaques de la cellule entraine la présence d’un champ électrique
-
Le champ électrique
-
Valeur du champ
E :
-
-
Les charges électriques
q présentes dans cet espace sont soumise à une force électrique :
-
2.
Migrations : a.
Signe de la charge portée par cette plaque ?
-
Les cations potassium
K+ migrent vers la plaque de droite D
:
-
La plaque de droite est chargée
négativement. b.
Migration des anions :
-
Les anions (ions chlorure
Cℓ–) migrent vers la plaque de gauche
G, chargée positivement.
![]() uniforme dans la région de
l’espace entre les plaques.
uniforme dans la région de
l’espace entre les plaques.![]() est orienté dans le sens des
potentiels décroissants.
est orienté dans le sens des
potentiels décroissants.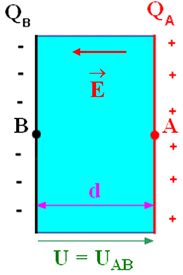
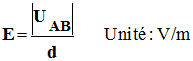
![]()
![]() dépend du signe de la charge q.
dépend du signe de la charge q.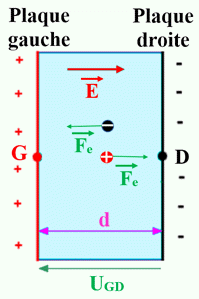
![]()
5)-Exercice 11 page 185 : Étudier un champ :
|
Étudier un champ :
Le schéma ci-dessus représente le champ électrostatique en quelques points d’un condensateur cylindrique. 1. Quel est le signe de la charge portée par l’armature centrale de ce condensateur ? 2.
Représenter le champ au point M. |
|
Étudier un champ :
1.
Signe de la charge portée par l’armature
centrale de ce condensateur :
-
Il découle de l’orientation du champ
électrique
que la charge portée par
l’armature centrale est positive.
-
Le champ électrique
charge portée par l’objet
source est positive.
2.
champ électrique
-
Dans l’espace entre les armatures, le
champ électrostatique est radial :
-
|
6)- Exercice 15 page 186 : Connaître le champ de gravitation :
|
Connaître le champ de gravitation :
La Lune est en interaction avec la terre. On note d la distance entre les centres des deux astres. 1. Exprimer la force exercée par la Terre sur la Lune en fonction de sa masse ML et du champ de
gravitation
2. Déduire de l’expression précédente l’unité de la valeur du champ de gravitation terrestre. 3. Schématiser, sans contrainte d’échelle, la force de gravitation exercée par la Terre sur la Lune et le champ de
gravitation terrestre existant en ce point.
-
Quelques données :
-
MT : masse de la
Terre : MT = 5,98 × 1024
kg.
-
ML : masse de la
Lune : ML = 7,34 × 1022 kg.
-
G est appelé la constante
de gravitation universelle :
-
G ≈ 6,67 × 10–11
m3 . kg–1 . s–2 ou m2 .
kg–2 . N
-
d : distance entre le centre
de la Terre et le centre de la Lune :
-
d = 3,84 × 105 km. |
|
Connaître le champ de gravitation :
1. Force exercée par la Terre sur la Lune en fonction de sa masse ML et du champ de
gravitation
-
-
Fg =
ML .
G
-
Expression de
G :
-
-
Expression vectorielle de
-
2.
Unité de la valeur du champ de gravitation
terrestre . - Les unités : en utilisant - Fg = ML
.
G
-
Ou
-
G ≈ 6,67 × 10–11
m3 . kg–1 . s–2 ou m2 .
kg–2 . N
-
-
Ou :
-
3. Schéma de la force de gravitation exercée par la Terre sur la Lune et du champ de gravitation terrestre
existant en ce point. -
Valeur de la force FT/L : -
-
Valeur du champ
G
exercée par la Terre sur la Lune : -
|
7)- Exercice 17 page 186 : Champ de pesanteur en haut de l’Everest :
|
Champ de pesanteur en haut de l’Everest :
L’Everest est la plus haute montagne du monde avec une altitude h = 8848 m. Son sommet se situe à une distance d = 6,382 ×106
m du centre de la Terre. 1. Exprime la valeur de la force de gravitation subie, au sommet de l’Everest, par un alpiniste de masse m en
fonction de G, d, m et MT, la
masse de la Terre. 2. Exprimer la valeur du poids de l’alpiniste en fonction de l’intensité de la pesanteur au sommet de L’Everest
gE. 3. En assimilant le poids à la force de gravitation, déterminer l’expression de la valeur du champ de pesanteur
en haut de l’Everest. 4.
Calculer cette valeur puis la comparer à
celle de ce champ au niveau de la mer.
-
Données :
-
G ≈ 6,67 × 10–11
m3 . kg–1 . s–2 ou m2 .
kg–2 . N
-
MT : masse de la
Terre : MT = 5,97 × 1024
kg.
-
gT = 9,81 N . kg–1
-
m = 80 kg. |
|
Champ de pesanteur en haut de l’Everest : 1. Expression de la valeur de la force de gravitation subie, au sommet de l’Everest, par un alpiniste.
-
2. Expression la valeur du poids de l’alpiniste en fonction de l’intensité de la pesanteur au sommet de L’Everest
gE.
-
P =
m .
gE 3.
Expression de la valeur du champ de
pesanteur en haut de l’Everest.
-
4.
Valeur puis comparaison à celle de ce champ
au niveau de la mer.
-
Valeur du champ de pesanteur en haut
de l’Everest :
-
-
Valeur de ce champ au niveau de la
mer
-
-
Comparaison gT et gE :
-
-
Comparaison gT0 et gE :
-
|
8)- Exercice 19 page 186 : Le sel de table :
|
Le sel de table : Le sel de table ou chlorure de sodium est un arrangement ordonné (cristal) d’ions chlorure et d’ions sodium. 1.
Calculer la valeur des forces
électrostatiques s’exerçant entre : a.
Un ion sodium et un ion chlorure voisins ; b.
Deux ions sodium les plus proches ; c.
Deux ions chlorure les plus proches. 2.
Proposer une explication sur la cohésion du
cristal du sel de table.
-
Données :
-
k = 9,0 × 109
N . m 2 . C–2.
-
e = 1,6 × 10–19
C |
Le sel de table : 1.
Valeur des différentes forces
électrostatiques : a.
Force électrostatique entre un ion sodium et
un ion chlorure voisin ;
-
L’ion sodium
Na+ provient d’un atome de sodium ayant perdu un
électron.
-
Il porte la charge électrique
+e.
-
L’ion chlorure
Cℓ– provient d’un atome de chlore ayant gagné un
électron.
-
Il porte la charge électrique
–e.
-
Expression de la force électrique
F1:
-
-
Force attractive. b.
Force électrostatique entre deux ions sodium
les plus proches :
-
-
Force répulsive. c.
Force électrostatique entre deux ions
chlorure les plus proches.
-
-
Force répulsive. 2.
Explication sur la cohésion du cristal du
sel de table.
-
Deux charges de mêmes signes se
repoussent et deux charges de signes contraires s’attirent.
-
Or :
F1 >
F2 =
F3
-
Les forces d’attraction sont
supérieures aux forces de répulsion.
-
L’interaction électrostatique
attractive, entre les ions sodium et les ions chlorure, assure la
cohésion du solide ionique.
-
Chaque ion est soumis à des forces
dont les effets se compensent.
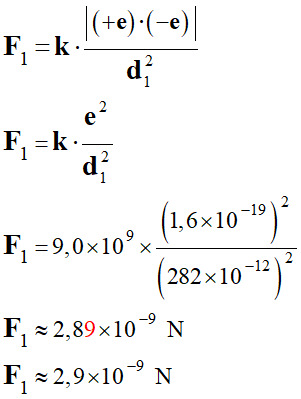
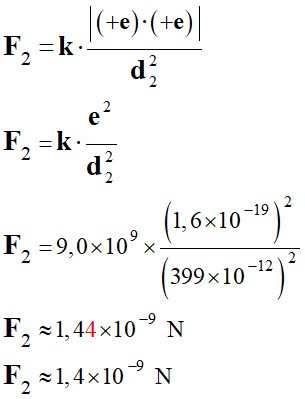
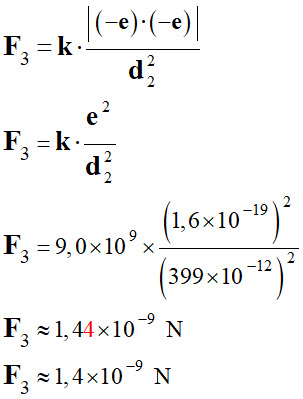
![]()
9)- Exercice 20 page 187 : Déviation des particules :
|
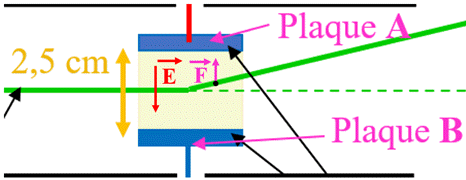
Déviation des particules : Joseph John Thomson, prix Nobel de physique en 1906, a notamment apporté les preuves de l’existence de l’électron. Il a montré que les rayons produits par un tube cathodique peuvent être déviés par un champ électrique dans un sens qui indique alors que les particules constituant le rayon cathodique sont chargées négativement. Dans cette expérience, la tension affichée par le voltmètre est de + 300 V, ce qui entraîne l’existence d’un champ électrostatique de direction perpendiculaire aux plaques. 1.
Identifier la plaque de déviation chargée
positivement lors de l’expérience. 2. Exprimer, en fonction du champ électrostatique, la force exercée sur une particule chargée
électriquement.. 3. Expliquer comment Joseph John Thomson a pu déterminer le signe de la charge des particules
constituant les rayons cathodiques. |
Déviation des particules : 1.
Plaque de déviation chargée positivement
lors de l’expérience.
-
Le voltmètre affiche la tension + 300
V.
-
La borne
V est reliée à la plaque
du haut
-
La borne
COM est reliée à la
plaque du bas.
-
D’après son branchement, la plaque de
déviation chargée positivement est la plaque du haut. 2.
Expression de la force exercée sur une
particule chargée électriquement.
-
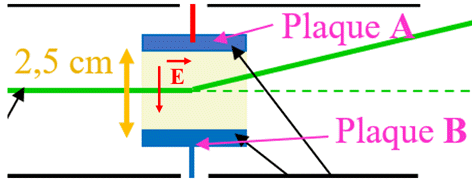
Champ électrique entre les plaques
A et
B :
-
Dans l’espace situé entre les
armatures, le champ électrique
-
Est considéré comme uniforme,
-
Sa direction est perpendiculaire aux
armatures,
-
Son sens est dirigé de l’armature
positive à l’armature négative (sens des potentiels décroissants),
-
Son intensité (sa valeur) :
-
-
Toute charge électrique q, située
dans cet espace, subit la force électrique suivante :
-
-
Les charges électriques sont déviées
vers le haut.
-
Elles sont donc soumises à la force
-
De même direction que le vecteur
champ électrique
-
Mais de sens opposé au vecteur champ
électrique
-
La charge électrique portée, par les
particules cathodiques, est négative.
-
Elles sont attirées par la plaque
chargée positivement.
![]() :
:![]()
![]()
![]() ,
, ![]()
![]()
![]()
11)- Exercice 25 page 188 : Champ de gravitation du Soleil et d’un trou noir :
|
Champ de gravitation du Soleil et d’un trou noir : A.
Le Soleil. - La Terre de masse MT, troisième planète du système solaire, gravite autour du Soleil à une distance dTS
= 1,50 ×1011 m du centre du Soleil, dont la masse est
MS = 2,0 × 1030
kg.
B.
Trou noir galactique. - Les trous noirs sont difficiles à détecter. Le trou noir Sagittarius A est situé au centre de la Voie lactée à d = 2,46 × 1020 m de la Terre. Sa masse M est 3,7 millions de fois plus grande que celle du Soleil.
1.
Exprimer la valeur de la force
gravitationnelle qu’exerce le Soleil sur la Terre. 2. Exprimer la valeur de cette force en fonction de la masse MT de la Terre et de celle GS du champ de gravitationnel du Soleil. 3.
Champ gravitationnel du Soleil. a. Déduire des deux questions précédentes l’expression de la valeur du champ gravitationnel du Soleil au
niveau de la Terre. b.
Calculer cette valeur. 4. Par analogie, exprimer puis calculer la valeur du champ de gravitation du trou noir Sagittarius A
au niveau de la Terre. 5.
Montrer à l’aide d’une comparaison que ce
trou noir ne perturbe pas le mouvement de la Terre.
-
Données :
-
G ≈ 6,67 × 10–11
m3 . kg–1 . s–2 ou m2 .
kg–2 . N |
|
Champ de gravitation du Soleil et d’un trou noir : 1. Expression la valeur de la force gravitationnelle qu’exerce le Soleil sur la Terre.
-
Schéma :
-
2. Valeur de cette force en fonction de la masse MT de la Terre et de celle
GS du champ de gravitationnel du Soleil.
-
FS/T =
MT .
GS 3.
Champ gravitationnel du Soleil. a. Expression de la valeur du champ gravitationnel du Soleil au niveau de la Terre.
-
Schéma :
-
b. Valeur du champ de gravitation GS exercé par le Soleil au niveau de la Terre.
-
4. Expression et valeur du champ de gravitation du trou noir Sagittarius A au niveau de la Terre.
-
Expression et valeur de
G :
-
5.
Comparaison de
GS et
G.
-
-
En conséquence
GS >>
G - Pour la Terre, le champ de gravitation G créé par le trou noir (Sagittarius A) est
négligeable devant celui créé par le Soleil. |
|
|