|
DS 02 (30 min) : Champ résultant au niveau de la Lune lors d’une
éclipse de Soleil :
1.
La force et le champ :
a.
Expression de la force exercée par la Terre sur
la Lune
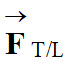 en fonction de ML, MT et
dTL. en fonction de ML, MT et
dTL.
-
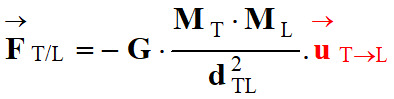
b.
Expression de cette force en fonction du champ
de gravitation de la Terre
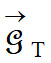 et de la masse de la Lune ML. et de la masse de la Lune ML.
-
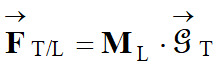
c.
Expression du champ de gravitation
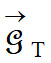 . .
-
2.
Expression du champ de gravitation
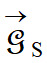 dû au Soleil. dû au Soleil.
-
Force exercée par le Soleil sur la Lune :
-
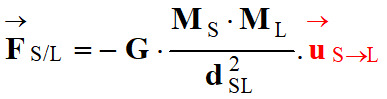
-
Expression du champ de gravitation 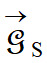 dû au Soleil : dû au Soleil :
-
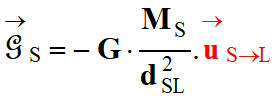
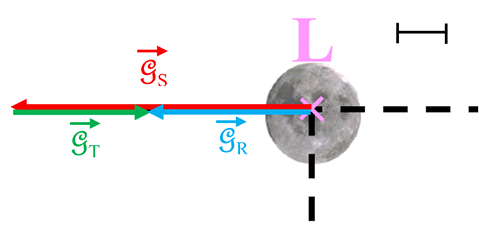
3.
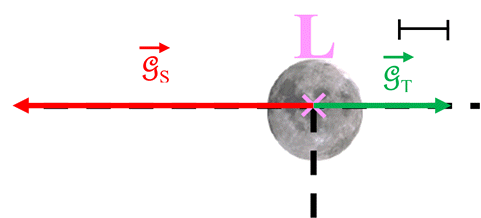
Représentation à l’échelle des deux champs
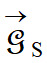 et et
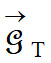 au niveau de la Lune. au niveau de la Lune.
-
Valeur du champ 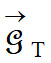 : :
-
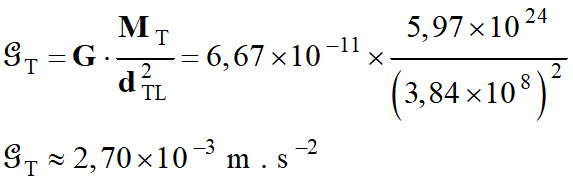
-
Le vecteur champ 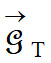 : :
-
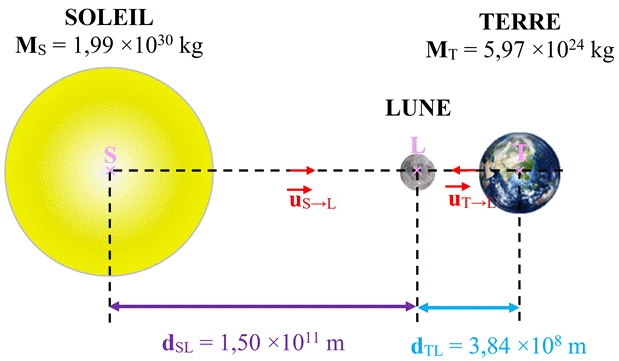
Direction : droite (TL)
-
Sens de
L vers
T
-
Valeur :
GT ≈ 2,70 × 10–3 m . s–2
-
Valeur du champ 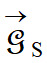 : :
-
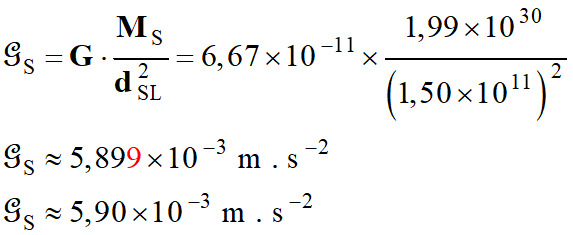
-
Le vecteur champ 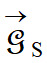 : :
-
Direction : droite (SL)
-
Sens de
L vers
S
-
Valeur :
GS ≈ 5,90 × 10–3 m . s–2
-
Remarque : les points
S, L et
T sont alignés. Les droites (SL)
et (TL) sont confondues.
-
Les deux champs
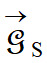 et et
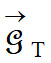 ont la même direction mais des
sens opposés. ont la même direction mais des
sens opposés.
-
Échelle : 1 cm ↔ 1,00 × 10–3 m
. s–2
-
Représentation :
-
Longueur du représentant de 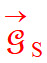 :
ℓS ≈ 5,9 cm :
ℓS ≈ 5,9 cm
-
Longueur du représentant de 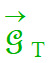 :
ℓT ≈ 2,7 cm :
ℓT ≈ 2,7 cm
4.
Caractéristiques du champ résultant
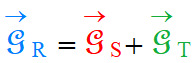 . .
-
Longueur du représentant du champ
résultant 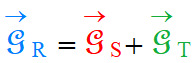 : :
-
ℓR
≈ 3,2 cm
-
Valeur du champ :
-
GS ≈ 3,2 × 10–3 m . s–2
-
Direction droite (SL) ou (TL)
-
Sens :
L vers
S.
-
Le vecteur champ résultant
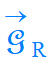 est orienté
vers le Soleil. est orienté
vers le Soleil.
|