|
Tableau d'avancement Exercices |
|
|
|
|
|
1)- Exercice 5 page 58 : Construire un tableau d’avancement :
|
Construire un tableau d’avancement : L’équation de la réaction s’écrit : 3 Fe (s) + 2 O2 (g)
→ Fe3O4 (s) Construire le tableau d’avancement associé à
cette réaction.
|
|
Construire un tableau d’avancement : 3 Fe (s) + 2 O2 (g) →
Fe3O4 (s)
-
Pour aller plus loin :
-
La réaction entre le fer Fe
(s) et le dioxygène O2 (g) est totale :
-
Alors à l’état final : x = xf
= xmax
-
Détermination de l’avancement
maximal : xmax
-
Hypothèse 1 : On considère que
le réactif limitant est le fer Fe (s) :
-
6,3
– 3 xmax1
=> xmax1
= 2,1 mol
-
Hypothèse 2 : On considère que
le réactif limitant est le O2
(g) :
-
4,6 – 2
xmax2 = 0 =>
xmax2 = 2,3 mol
-
L’avancement maximal est égal à la
plus petite des deux valeurs :
-
Car on ne peut pas consommer plus de
réactif qu’il n’y en a au départ
-
xmax = xmax1
= 2,1 mol ≤ xmax2
-
On peut maintenant compléter le
tableau d’avancement de la réaction.
-
Le fer Fe (s) est le réactif
limitant. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2)- Exercice 6 page 58 : Utiliser un tableau d’avancement :
|
Utiliser un tableau d’avancement :
2.
Calculer les quantités de matière des
réactifs et des produits
pour x = 3,2 mmol. |
||||||||||||||||||||||
|
Utiliser un tableau d’avancement :
- En considérant que la réaction est totale, on peut calculer la valeur de l’avancement maximal xmax
et déterminer l’étal final du système chimique.
-
Alors à l’état final : x = xf
= xmax
-
Détermination de l’avancement
maximal : xmax
-
Hypothèse 1 : On considère que
le réactif limitant est le magnésium
Mg (s) :
-
10 –
2 xmax1
=> xmax1
= 5,0 mmol
-
Hypothèse 2 : On considère que
le réactif limitant est le O2 (g) :
-
4,0 – xmax2 = 0 =>
xmax2 = 4,0 mmol
-
L’avancement maximal est égal à la
plus petite des deux valeurs :
-
Car on ne peut pas consommer plus de
réactif qu’il n’y en a au départ
-
xmax = xmax2
= 4,0 mmol ≤ xmax1
-
On peut maintenant compléter le
tableau d’avancement de la réaction.
- Le réactif limitant est le dioxygène O2 (g). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3)- Exercice 9 page 59 : Déterminer la composition d’un système à l’état final :
|
Déterminer la composition d’un système à l’état final : forment un précipité jaune d’iodure de plomb (II), PbI2
(s) appelé « pluie d’or ».
Le tableau d’avancement de la réaction étudiée, associée à une transformation totale est donné ci-dessous :
1.
Reproduire et compléter le tableau
d’avancement. 2.
Déterminer la valeur de l’avancement maximal
xmax. 3.
En déduire la composition du système
chimique dans l’état final. |
||||||||||||||||||||||||||||
Déterminer la composition d’un système à l’état final : 1.
Tableau d’avancement. Équation
Pb2+
(aq)
+
2 I–
(aq)
→
PbI2
(s)
État du
système
Avanc.
mmol
n (Pb2+)
mmol
n (I–)
mmol
n (PbI2)
mmol
État initial
(mmol)
x =
0
5,0
5,0
0
État
Intermédiaire
(mmol)
x
5,0 – x
5,0 – 2 x
x
État final
(mmol)
xf =
xmax
5,0 – xmax
5,0 – 2 xmax
xmax 2.
Valeur de l’avancement maximal xmax.
-
La transformation est totale :
-
Alors à l’état final : x = xf
= xmax
-
Détermination de l’avancement
maximal : xmax
-
Hypothèse 1 : On considère que
le réactif limitant est l’ion
Pb2+ (aq):
-
5,0 –
xmax1
=> xmax1
= 5,0 mmol
-
Hypothèse 2 : On considère que
le réactif limitant est l’ion
I– (aq) :
-
5,0 – 2
xmax2 = 0 => xmax2 = 2,5 mmol
-
L’avancement maximal est égal à la
plus petite des deux valeurs :
-
Car on ne peut pas consommer plus de
réactif qu’il n’y en a au départ
-
xmax = xmax2
= 2,5 mmol ≤ xmax1
-
On peut maintenant compléter le
tableau d’avancement de la réaction. 3.
Composition du système chimique dans l’état
final. Équation
Pb2+
(aq)
+
2 I–
(aq)
→
PbI2
(s)
État du
système
Avanc.
mmol
n (Pb2+)
mmol
n (I–)
mmol
n (PbI2)
mmol
État initial
(mmol)
x =
0
5,0
5,0
0
État
Intermédiaire
(mmol)
x
5,0 – x
5,0 – 2 x
x
État final
(mmol)
xf =
xmax
5,0 – xmax
5,0 – 2 xmax
xmax
2,5
2,5
0
2,5

![]()
4)- Exercice 11 page 59 : Comparer les avancements final et maximal :
|
Comparer les avancements final et maximal : Le méthanol CH4O réagit avec l’acide méthanoïque CH2O2 pour former un ester, le méthanoate de méthyle C2H4O2
et de l’eau. On suppose que cette transformation
est totale. Le tableau d’avancement de la réaction étudiée est alors :
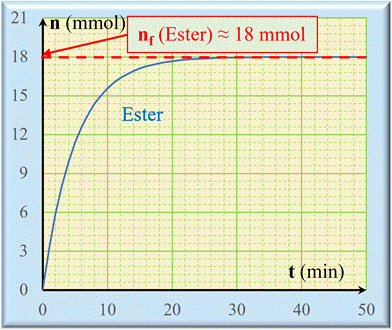
Le graphique
ci-dessous donne l’évolution de la quantité d’ester formé au cours
du temps.
1.
Déterminer graphiquement la valeur de
l’avancement final xf. Justifier. 2.
Calculer la valeur de l’avancement maximal
xmax en s’aidant du tableau d’avancement. 3.
Comparer xf et xmax ;
commenter la phrase en italique de l’énoncé. |
|||||||||||||||||||||||||||||||||
Comparer les avancements final et maximal : 1.
Détermination graphique de la valeur de
l’avancement final xf. -
Au cours du temps, la quantité de matière
d’ester augmente puis atteint une valeur limite. -
La lecture graphique de la valeur limite
donne : -
n
(C2H4O2) ≈ 18
mmol -
D’après le tableau d’avancement, on remarque
que dans l’état final du système chimique : -
n (C2H4O2)
= xf -
En fin de réaction lorsque l’état final est
atteint : -
n (C2H4O2)
= xf ≈ 18 mmol 2.
Valeur de l’avancement maximal xmax
. -
En considérant que la transformation est
totale, on peut déterminer la valeur de l’avancement maximal xmax. -
Hypothèse 1 : On considère que le
réactif limitant est le méthanol
CH4O
: -
27 –
xmax1
=> xmax1
= 27 mmol -
Hypothèse 2 : On considère que le
réactif limitant est l’acide méthanoïque
CH2O2
: -
27 – xmax2 = 0 => xmax2
= 27 mmol -
xmax = xmax1
= xmax2 = 27 mmol 3.
Comparaison de xf et xmax ;
-
On remarque que xmax = 27
mmol et xf ≈
18 mmol -
xf
< xmax -
En conclusion, la transformation entre le
méthanol CH4
et l’acide méthanoïque CH2O2 est non totale. -
La phrase en italique n’est pas vérifiée
pour cette transformation chimique.
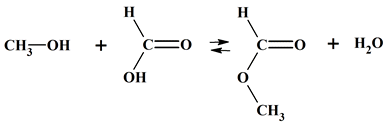
Équation
CH4O
+
CH2O2 →
C2H4O2 +
H2O
État du
système
Avancement
n
(CH4O)
(mmol)
n
(CH2O2)
(mmol)
n
(C2H4O2)
(mmol)
n
(H2O)
(mmol)
État initial
(mmol)
x =
0
27
27
0
0
État
intermédiaire
0
≤ x ≤ xf
27 – x
27 – x
x
x
État final
(mmol)
x = xf
≈ 18
27 – xf
27 – xf
xf
xf
18
9
9
18
18 -
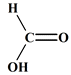
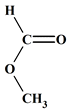
La réaction d’estérification : - La réaction d’estérification est la réaction d’un acide
carboxylique sur un alcool. - Elle donne un ester et de l’eau. - Dans le cas présent : Méthanol
CH3
– OH
Acide méthanoïque
(Acide formique)
Méthanoate
de méthyle
(Formiate de méthyle)
Eau
H2O -
Caractéristiques de la réaction d’estérification :
La réaction est limitée,
il y a coexistence dans la même
solution
des réactifs et des produits.
Le système n’évoluant plus dans
le temps,
cet état est caractéristique
d’un équilibre chimique.
-
La réaction d’estérification et la réaction d’hydrolyse :
état d’équilibre. - La réaction d’estérification est une
réaction lente, limitée et athermique. - Il en est de même de la réaction
d’hydrolyse. - Les réactions d’estérification et
d’hydrolyse d’un ester sont des réactions inverses se produisant
dans les mêmes conditions expérimentales. -
L’état final obtenu est le même que l’on parte d’un mélange
équimolaire d’acide carboxylique et
d’alcool ou d’ester et d’eau. -
Dans l’état final, les proportions des différents composés
n’évoluent plus au cours du temps. -
On est en présence d’un état d’équilibre. -
C’est un équilibre chimique dynamique. -
Les vitesses des deux réactions
inverses sont égales et annulent ainsi leurs effets.
![]()
5)- Exercice 12 page 59 : Déterminer l’état d’un système chimique :
|
Déterminer l’état d’un système chimique : L’hydroxyde de fer (III) Fe(OH)3 (s) est
un solide orange obtenu à partir de la réaction d’équation : Fe3+ (aq) + 3 HO–
(aq) → Fe(OH)3 (s) Initialement, le système chimique contient 3,0 mmol d’ions fer (III) Fe3+ (aq) et 12,0 mmol d’ions hydroxyde HO– (aq). 1.
Déterminer l’état du système chimique pour
les avancements x = 1,0 mmol et x
= 2,0 mmol. 2.
L’avancement final du système est xf
= 3,0 mmol. La transformation est-elle
totale ? |
|
Déterminer l’état d’un système chimique : 1.
État du système chimique pour les
avancements x = 1,0 mmol et x = 2,0 mmol. -
Le mieux est de construire un tableau
d’avancement de la réaction.
-
L’avancement final du système est xf
= 3,0 mmol. -
Tableau d’avancement.
-
On remarque que n (Fe3+)
= 0,0. -
L’ion fer (III),Fe3+
(aq) est le réactif limitant. -
La réaction s’arrête par manque d’un des deux réactifs. -
La réaction est totale : xf = xmax
= 3,0 mmol -
Autre méthode : - On peut l’hypothèse que la réaction est totale et calculer la valeur de l’avancement maximal xmax et comparer cette valeur à celle de l’avancement final
xf. -
Détermination de l’avancement maximal : xmax -
Hypothèse 1 : On considère que le
réactif limitant est l’ion Fe3+ (aq): -
3,0
–
xmax1
=> xmax1
= 3,0 mmol -
Hypothèse 2 : On considère que le
réactif limitant est l’ion HO–
(aq) : -
12,0 – 3 xmax2
= 0 => xmax2 = 4,0 mmol -
L’avancement maximal est égal à la plus
petite des deux valeurs : -
Car on ne peut pas consommer plus de réactif
qu’il n’y en a au départ -
xmax = xmax1
= 3,0 mmol ≤ xmax2 -
Conclusion : xmax = xf
= 3,0 mmol -
La réaction est totale.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6)- Exercice 14 page 60 : Identifier des relations de stœchiométrie :
|
Identifier des relations de stœchiométrie : L’hématite Fe2O3 (s) est
obtenue par combustion du fer Fe (s) dans le dioxygène O2 (g)
selon la réaction
d’équation : 4 Fe (s) +
3 O2 (g) →
2 Fe2O3
(s) -
Parmi les relations suivantes, identifier
celles qui correspondent à un mélange initial stœchiométrique. 1.
2. 3.
n0
(Fe) = n0 (O2) 4.
3 n0 (Fe) = 4 n0
(O2) |
|
Identifier des relations de stœchiométrie : -
Identification des bonnes relations :
-
On peut s’aider d’un tableau pour retrouver la relation entre
les quantités de matière de réactifs pour préparer un mélange stœchiométrique. 4 Fe (s) +
3 O2 (g) →
2 Fe2O3
(s)
- La relation pour un mélange stœchiométrique apparaît dans le tableau. - La
relation qui lie le quantités de matière de réactifs est la
suivante : -
- Autre
formulation : 3 n0 (Fe) = 4 n0
(O2) : réponse 4.
|
|||||||||||||||||||||||
7)- Exercice 17 page 60 : L’acide citrique :
|
L’acide citrique : C6H8O7
(aq) + 3 HO– (aq) → C6H5O73–
(aq) + 3 H2O (ℓ) Les graphiques a et b ci-dessous
donnent les quantités initiales des réactifs, en mol.
1.
Mélange stœchiométrique : b.
Déterminer les quantités des produits dans
l’état final. 2.
Mélange quelconque : a.
Déterminer l’avancement maximal xmax
et le réactif limitant pour l’autre mélange initial. b.
Réaliser un histogramme représentant les
quantités d’acide citrique, d’ions hydroxyde et d’ions
citrate C5H5O73–
(aq) : -
Pour un état intermédiaire
x = 1,0 mol ; -
À l’état final. 3.
Pourquoi ne pourrait-on pas représenter la
quantité d’eau dans les histogrammes ?
|
|
L’acide citrique : -
On connait l’équation de la réaction : C6H8O7
(aq) + 3 HO– (aq) → C6H5O73–
(aq) + 3 H2O (ℓ) -
Pour que le mélange soit stœchiométrique, il
faut que les quantités de matières initiales des réactifs respectent la relation
suivante : -
-
Ou plus simplement :
3
n0 (C6H8O7) =
n0
(HO–) -
Il faut 3 fois plus de quantité de matière
l’ions hydroxyde que d’acide citrique. -
Le bon mélange est le graphique
b : -
n0
(C6H8O7)
= 4 mol et n0
(HO–) = 12 mol b.
Quantités des produits dans l’état final. -
Tableau d’avancement : La réaction est
totale : xf
= xmax
-
Remarque : - On a fait le calcul pour l’eau, mais il n’est pas nécessaire. - L’eau est le solvant de la réaction. -
L’eau est le solvant de la solution aqueuse
qui contient les ions hydroxyde. -
Lorsque cela est le cas, la colonne où l’eau
intervient n’est pas remplie.
a.
Avancement maximal xmax et
le réactif limitant pour l’autre mélange initial. -
Graphique
a :
n0 (C6H8O7)
= 10 mol et n0
(HO–) = 12 mol -
Les proportions stœchiométriques
de l’équation ne sont pas
respectées. -
3
n0 (C6H8O7)
> n0 (HO–) -
On peut faire le raisonnement systématique,
mais on remarque que le réactif limitant est l’ion hydroxyde et que
l’acide citrique est en excès. -
Hypothèse 1 : On considère que le
réactif limitant est l’acide citrique
C6H8O7 (aq) : -
10 –
xmax1
=> xmax1
= 10 mol -
Hypothèse 2 : On considère que le
réactif limitant est l’ion hydroxyde
HO– (aq : -
12 – 3 xmax2
= 0 => xmax2 = 4,0 mol -
xmax = xmax2
= 4,0 mmol < xmax1
-
l’ion hydroxyde est bien le réactif
limitant. b.
Histogramme représentant les quantités
d’acide citrique, d’ions hydroxyde et d’ions citrate C5H5O73–
(aq) : -
État intermédiaire
x = 1,0 mol :
-
Histogramme :
-
État final.
3.
Quantité d’eau dans les histogrammes : -
Les ions hydroxyde proviennent d’une
solution aqueuse (la soude entre autres ) dont l’eau est le solvant. -
La soude : solution aqueuse d’hydroxyde de
sodium : {Na+
(aq) + HO–
(aq)} -
L’eau étant le solvant, elle est en large
excès et ne peut apparaître dans l’histogramme. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
8)-Exercice 19 page 61 : Réaction entre le métal magnésium et l’acide chlorhydrique :
|
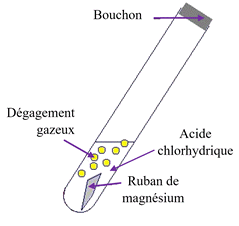
Réaction entre le métal magnésium et l’acide chlorhydrique :
A.
Expérience : À l’aide d’une caméra reliée à un ordinateur, on filme la transformation chimique entre le magnésium et l’acide chlorhydrique. Le dihydrogène formé lors de l’expérience est récupéré dans une éprouvette graduée. Le schéma de l’expérience est reproduit ci-dessous.
B.
Évolution du volume de dihydrogène au cours du temps :
-
Données :
1.
Pourquoi avoir utilisé une éprouvette
remplie d’eau et retournée sur le cristallisoir pour cette
expérience ? 2.
Proposer un test permettant de mettre en
évidence le gaz dihydrogène dans l’éprouvette graduée. 3.
Identifier les couples oxydant réducteur mis
en jeu lors de cette réaction d’oxydoréduction. 4.
Calculer les quantités initiales des
réactifs. 5.
Identifier le réactif limitant. 6. À l’aide du graphique B., déterminer graphiquement la valeur du volume de dihydrogène V (H2) à l’état final et en déduire la valeur de l’avancement final xf de la
réaction. 7.
La transformation est-elle totale ?
Justifier. |
||||||
Réaction entre le métal magnésium et l’acide chlorhydrique : 1.
Utilisation de l’éprouvette remplie d’eau : -
L’éprouvette graduée permet de récupérer le
dihydrogène gazeux par déplacement de liquide. -
Le dihydrogène étant plus léger que l’eau va
monter dans l’éprouvette graduée et prendre la place de l’eau. -
Ainsi on peut par simple lecture déterminer
la valeur du volume de dihydrogène formé au cours de l’expérience. -
Il faut faire en
sorte que la pression du gaz dans l’éprouvette soit sensiblement
égale à la pression atmosphérique. -
L’expérience se déroule à la pression atmosphérique si on équilibre
les niveaux. 2.
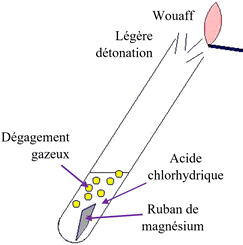
Test permettant de mettre en évidence le gaz
dihydrogène dans l’éprouvette graduée. -
Le gaz qui
produit une légère détonation en présence d’une flamme est le
dihydrogène H2. 3.
Couples oxydant réducteur mis en jeu lors de
cette réaction d’oxydoréduction. -
Couple 1 :
Mg2+ (aq) /
Mg
(s) -
Couple 2 : H+
(aq) / H2 (g) 4.
Quantités initiales des réactifs. -
Quantité de matière initiale de magnésium : -
-
Quantité de matière d’ions hydrogène : -
n0
(H+) = C .
V = 0,50 × 40 × 10–3 -
n0
(H+) ≈ 2,0 × 10–2 mol 5.
Le réactif limitant. -
On peut faire l’hypothèse que la réaction
est totale. Mg (s) + 2 H+ (aq) →
Mg2+ (aq) + H2 (g) -
On peut ainsi calculer l’avancement maximal
pour chaque réactif : -
Hypothèse 1 : On considère que le
réactif limitant est le magnésium
Mg (s) : -
5,0 × 10–3
–
xmax1
=> xmax1
= 5,0 × 10–3 mol -
Hypothèse 2 : On considère que le
réactif limitant est l’ion hydrogène H+ (aq : -
2,0 × 10–2 –
2 xmax2 = 0 => xmax2
= 1,0 × 10–2 mol -
xmax = xmax1
= 5,0 × 10–3 mol < xmax2 6.
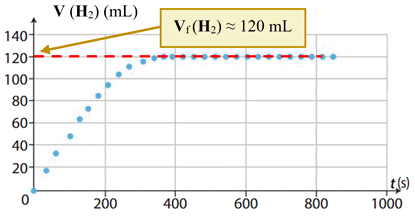
Détermination graphique de la valeur du
volume de dihydrogène V (H2). -
Volume de dihydrogène en fin de réaction : -
Vf (H2)
≈ 120 mL -
Quantité de matière correspondante : -
-
En fin de réaction, à l’état final, la
quantité de matière de dihydrogène formé est égale à l’avancement
final de réaction : -
nf (H2)
= xf ≈ 5,0
× 10–3 mol -
Valeur de l’avancement final
xf de la réaction : -
xf ≈ 5,0 × 10–3
mol -
Tableau d’avancement : Équation
Mg
(s)
+ 2
H+ (aq)
→
Mg2+
(aq) +
H2 (g)
État du
système
Avanc.
n (Mg)
(mol)
n (H+)
(mol)
n (Mg2+)
(mol)
n (H2)
(mol)
État initial
(mol)
x =
0
5,0 ×
10–3
2,0 ×
10–2
0
0
État
intermédiaire
0 ≤ x ≤ xf
5,0 ×
10–3 –
x
2,0 ×
10–2 –
2
x
x
x
État
Final
(mol)
xf
5,0 ×
10–3 –
xf
2,0 ×
10–2 –
2
xf
xf
xf
5,0 ×
10–3
0
1,0 ×
10–2
5,0 ×
10–3
5,0 ×
10–3 7.
Transformation totale ou non totale : -
Comme
xf = xmax
≈ 5,0 × 10–3
mol -
La réaction est totale.
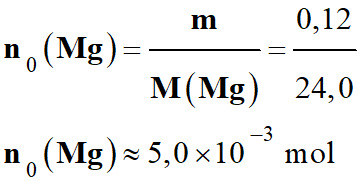
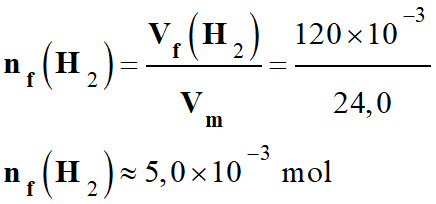
![]()
|
|