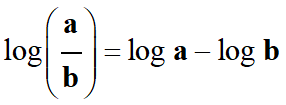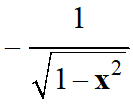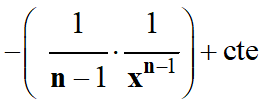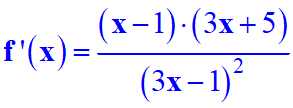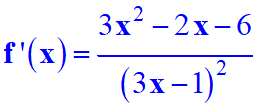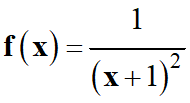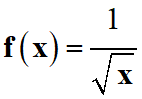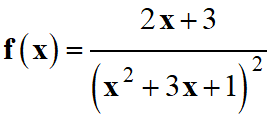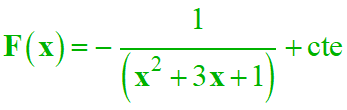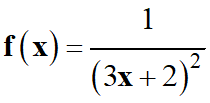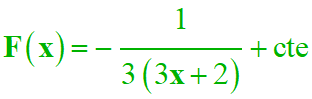|
Math
|
Math pour les sciences physiques |
|
|
|
|
Rappels
de Math pour les sciences physiques :
-
On
appelle dérivée d’une fonction au point
x0,
la limite si elle existe de la fonction :
-

-
On note : 
-
Autre définition :
-
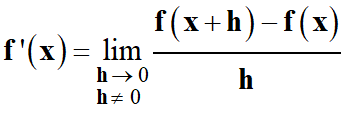
-
Soit
f
(x)
= x2
-
Déterminer la fonction dérivée de
f
(x)
= x2
-
On applique la
définition :
-
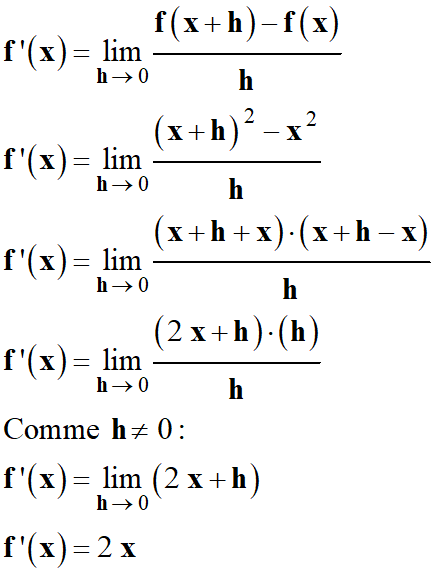
|
Dérivée d’une
somme |
(f +
g)’ = f’ + g’ |
|
Dérivée d’un
produit |
(f .
g)’ = f’ . g + f . g’ |
|
Dérivée d’un
quotient |
|
-
Posons : x
= x0
+ dx ;
la grandeur dx
représente un infiniment petit.
-
Nouvelle écriture :
- ![]()
-
Pour la
fonction f
(x)
continue et dérivable,
f’ (x)
représente la fonction dérivée de
f
(x)
-
Conséquence : ![]()
-
Posons :
-
df
(x)
= f
(x
+ dx)
– f
(x)
-
La
grandeur df
(x)
représente une variation infinitésimale de la fonction
f
(x).
-
Autre notation
différentielle : ![]()
-
Ou
encore : df
= f’
(x)
.
dx
-
f’
(x) :
dérivée de la fonction
f (x)
par rapport à x.
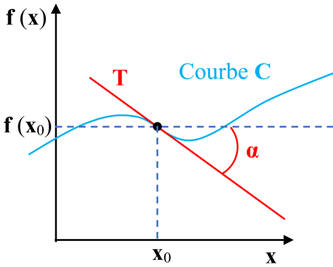
5)- Interprétation graphique :
-
Si l’on
calcule f’
(x0),
le nombre dérivé donne le coefficient directeur
a
de la tangente T
à la courbe C
au point d’abscisse
x0.
-
Schéma :
-
f’
(x0)
= a
= tan α
|
f
(x) |
f‘(x) |
|
a |
0 |
|
a
. x + b |
a |
|
a
. x2 + b . x + c |
2 a .
x + b |
|
cos x
|
– sin x |
|
cos (a
. x) |
– a sin
(a . x) |
|
sin x
|
cos x |
|
sin (a
. x) |
a cos (a .
x) |
7)- Application directe en physique :
-
La
fonction intensité instantanée
i est la fonction dérivée de la
fonction charge électrique
q par rapport au temps
t.
-
Notation différentielle :
![]() ou
i =
q’
(t)
ou
i =
q’
(t)
-
En physique, lorsque
la variable est le temps, on utilise la notation suivante :
- ![]()
-
Remarque :
-
Si
q
= a
. t =>
![]()
-
Si
q
= a =>
![]()
8)- Fonction de plusieurs variables : Dérivées
partielles.
a)-
Dérivées partielles :
-
Soit
f
(x,
y) :
-
d f
(x,
y) =
f’x
. dx
+ f’y
.
dy
-
La
fonction f’x
représente la
dérivée partielle de
f
(x,
y) par
rapport à x,
-
y
étant supposé constant.
-
La
fonction f’y
représente la
dérivée partielle de
f
(x,
y) par
rapport à y,
-
x
étant supposé constant.
-
On note :
-

- 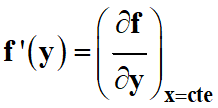
-
On tire l’expression
suivante :
- 
b)-
Application 1 :
-
Déterminer l’expression de
df (x,
y),
sachant que f
(x,
y)
= 4 x
+ 5
y2
-
On part de la formule
générale :
-

-
Il faut
calculer
![]() , c’est-à-dire la dérivée de l’expression
f
(x,
y)
= 4 x
+ 5
y2 par
rapport à x,
en considérant que
y est assimilable à une constante.
, c’est-à-dire la dérivée de l’expression
f
(x,
y)
= 4 x
+ 5
y2 par
rapport à x,
en considérant que
y est assimilable à une constante.
- 
-
Il faut
calculer
![]() , c’est-à-dire la dérivée de l’expression
f
(x,
y)
= 4 x
+ 5
y2 par
rapport à y,
en considérant que
x est assimilable à une constante.
, c’est-à-dire la dérivée de l’expression
f
(x,
y)
= 4 x
+ 5
y2 par
rapport à y,
en considérant que
x est assimilable à une constante.
-
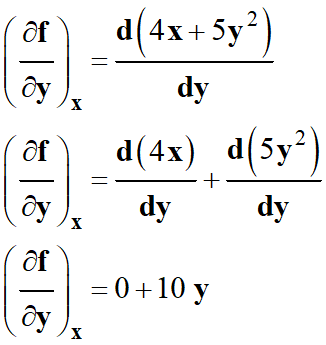
-
En conclusion :
- 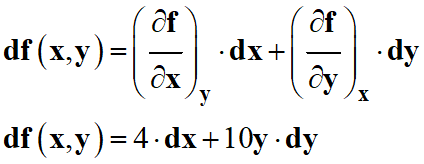
c)-
Application 2 :
-
Déterminer l’expression de
df (x,
y),
sachant que f
(x,
y)
= 4 x2
×
y3
-
Par définition :
-

-
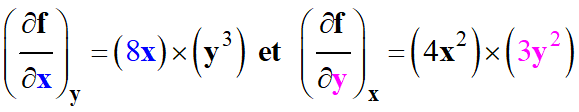
-
df
(x,
y)
= (8 x
y3) .
dx
+ (12 x2
y2)
. dy
►
Propriétés :
|
(1) |
|
|
(2) |
|
►
Autres propriétés :
|
|
f
= u . v |
|
(1) |
Si f
= u . v => df= u . dv + v . du |
|
(2) |
|
|
(3) |
Si f =
cte => df = 0 |
d)-
Application 3 :
-
Déterminer les expressions de
df et
dg
de deux façons différentes sachant que :
-
f
=
x cos (y)
et g = x sin
(y)
-
Méthode 1 :
-
Détermination de
df :
-
df
= cos (y)
. dx
+ x
. d
[cos (y)]
-
Pour
déterminer d
[cos(y)],
fonction d’une seule variable, il faut utiliser le fait que :
-
df
= f’
.
dx
-
Dans le
cas présent, il faut trouver la dérivée de [cos(y)]
par rapport à y :
-

-
On tire :
-
df
= cos (y)
. dx
– x
. sin (y)
. dy
-
De même
pour la fonction g = x sin(y)
-
dg
= sin (y) .
dx +
x . cos (y)
. dy
-
Méthode 2 :
-
On utilise la
définition :
- 
-
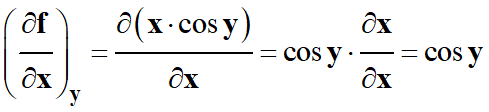
-
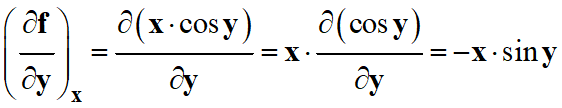
-
En conclusion :
-
df
(x,
y)
= cos (y) .
dx –
x . sin (y)
. dy
►
Remarque : Cas de
trois variables : f
(P,
V,
T)
-

-
F
(x)
est une primitive de
f (x)
si la dérivée F’
(x)
= f
(x).
-
En utilisant
l’écriture différentielle :
- 
-
Remarque :
-
Soit la
fonction G
(x)
= F
(x)
+ a
(la grandeur a
étant une constante par rapport à
x)
-
G’
(x) =
F’ (x)
+ 0 =
f
(x)
-
La
fonction G
(x)
est aussi une primitive de
f (x).
►
Question 1 :
-
Soit
F (x)
= x3.
-
Déterminer la fonction
f (x)
dont elle est la primitive.
►
Réponse 1 :
-
Par définition :
-
F’
(x)
= f
(x)
-
F’
(x)
= 3 x2
= f
(x)
►
Question 2 :
-
Déterminer la
primitive F
(x)
de la fonction f
(x)
= x2.
►
Réponse 2 :
-
Il faut trouver la
fonction F (x)
telle que F’
(x)
= x2.
-
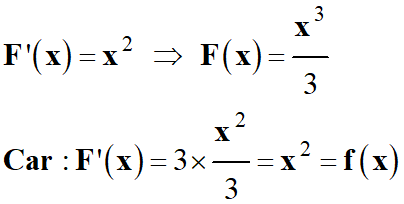
-
De même :
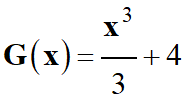 est aussi
solution.
est aussi
solution.
-
En général :
- 
-
Une primitive est
connue à une constante près.
3)- Exemple d’application en physique :
-
Considérons le fonction
x (t)
qui dépend du temps
t
-
Elle
peut représenter l’abscisse d’un point mobile
M.
-
![]() représente
la dérivée première par rapport au temps
t.
représente
la dérivée première par rapport au temps
t.
- ![]() représente la dérivée seconde par rapport au temps
t.
représente la dérivée seconde par rapport au temps
t.
►
Exemple :
-
On considère la
situation suivante :
-
![]() ; la
grandeur a
est une constante par rapport au temps
t.
; la
grandeur a
est une constante par rapport au temps
t.
-
Le but
est de déterminer la fonction
x (t),
sachant que
![]() .
.
-
On passe par
l’intermédiaire de la dérivée
![]() :
:
- ![]() est une primitive de
est une primitive de
![]()
-
Comme ![]()
-
Il
apparaît la constante
b, car la primitive est connue à une
constante près.
-
En physique, cette
constante est liée aux conditions initiales.
-
Deux cas se
présentent :
|
|
b
= 0 |
|
|
|
2 cas |
|
=> |
|
|
|
b
≠ 0 |
|
|
-
De même
x
est une primitive de
![]() :
:
-
En conséquence :
|
|
|
ou |
|
|
-
Les
grandeurs b
et c
sont liées aux conditions initiales.
|
f
(x) |
Primitive F
(x) |
|
0 |
cte |
|
a |
a
. x + cte |
|
xn |
|
|
sin x
|
– cos x
+ cte |
|
sin (a
. x) |
|
|
cos x
|
sin x +
cte |
|
cos (a
. x) |
|
|
|
ln |x| + cte |
5)- Fonction logarithme et fonction
exponentielle :
a)-
La fonction logarithme
népérien :
-
La fonction logarithme
népérien : ln
-
Domaine
de définition : R*+
|
x |
→ |
ln x |
|
R*+ |
|
R |
-
Fonction continue
strictement croissante
►
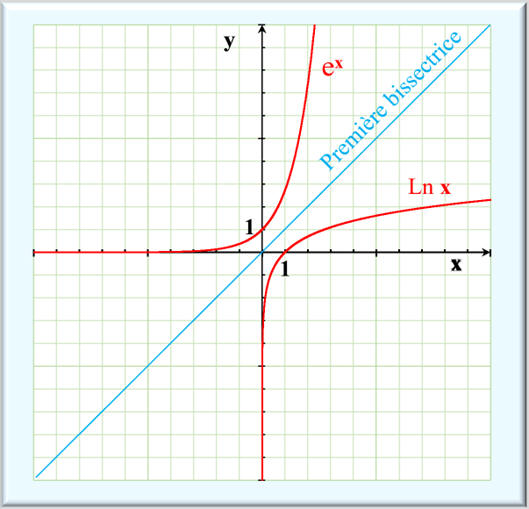
Graphe :
►
La fonction
exponentielle :
-
La fonction
exponentielle est la fonction inverse de la fonction logarithme népérien :
|
y = ex |
<=>
|
x
= ln y |
|
x
€ R |
|
y € R*+ |
-
e0
= 1
►
Propriétés :
|
ln 1 = 0 |
|
ln (a ×
b) = ln a + ln b
|
|
|
|
ln an
= n ln a avec n € Z |
►
Remarque :
-
Pour les calculs
pratiques, on utilise le logarithme à base 10 (logarithme décimal)
|
y = 10x |
<=>
|
x
= log y |
|
x
€ R |
|
y € R*+ |
►
Propriétés : la
fonction logarithme décimal a les mêmes propriétés que la fonction logarithme
népérien.
|
log 1 = 0 |
|
log (a
× b) = log a + log b
|
|
|
|
log 10n
= n log 10 = n avec n € Z |
►
Calcul de la
concentration en ion oxonium :
-
Calculer la
concentration en ion oxonium H3O+
(aq) d’une solution dont le
pH est égal à 4,5
-
Le
pH
d’une solution est un indicateur d’acidité lié à la présence des ions oxonium
H3O+ (aq)
en solution.
|
Pour une
solution diluée, [H3O+]
< 0,050 mol . L–1, Le pH
est défini par la relation suivante :
Cette
relation est équivalente à :
|
|
pH :
grandeur sans unité |
|
[H3O+] :
concentration en ions oxonium en mol . L–1 |
|
C0 :
concentration standard : C0 = 1,0 mol . L–1 |
-
Remarques :
-
On
écrit aussi : pH
= – log [H3O+] (relation
utilisée jusqu’en 2010)
-
pH
= 4,5 => [H3O+] =
C0
× 10–pH
-
[H3O+] =
C0
× 10–4,5
-
[H3O+] ≈
3,2 × 10–5 mol . L–1
-
Il faut arrondir et
garder au maximum 2 chiffres significatifs.
►
Calcul de pH :
-
La concentration en
ion oxonium d’une solution aqueuse est :
-
[H3O+] =
2,5 × 10–3 mol . L–1
-
En déduire la valeur
du pH de cette solution.
-
Le
pH est défini par
la relation suivante :
-
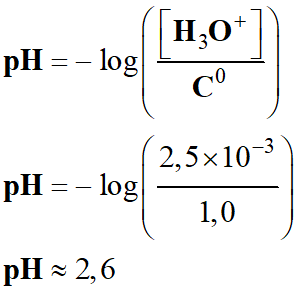
a)-
Définition :
-
Intégrale définie :
-
![]()
-
Si la
fonction f
admet des primitives et si
F est une de ses primitives.
- ![]()
-
F
(x)
est une primitive de
f (x).
-
Autre écriture :
-
![]()
b)-
Applications :
-
Calculer ![]()
-
On
cherche une primitive de
x3 (la
plus simple)
|
f
(x) |
|
Primitive F
(x) |
|
f
(x)
= x3 |
→ |
|
-
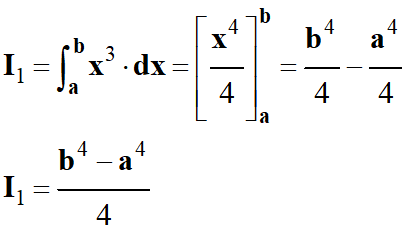
-
Il n’est pas
nécessaire de mettre une constante (elle disparaît par différence).
►
Exemples :
-
![]()
-
![]()
-
![]()
- ![]()
7)- Retour sur la fonction logarithme népérien :
-
On
appelle fonction logarithme népérien de
x,
la fonction définie par :
-
![]()
-
La
fonction ln x
est la primitive de la fonction ![]()
-
ln 1 = 0
-
![]()
8)- Retour sur la fonction exponentielle :
-
La fonction
exponentielle, notée
ex
est la fonction inverse de la fonction logarithme népérien.
-
Par définition :
|
y = ex |
|
x
= ln y |
|
x
€ R |
|
y € R*+ |
►
Propriétés :
|
(ex)’
= ex ou d (ex)
= (ex) . dx |
|
|
|
|
|
|
III-
Tableau des dérivées usuelles
|
f
(x) |
f‘(x) |
|
cte |
0 |
|
a
. x |
a |
|
a
. x + b |
a |
|
x2 |
2 x |
|
a
. x2 + b . x + c |
2 a .
x + b |
|
xn
|
n
. xn–1 |
|
|
|
|
|
|
|
cos x
|
– sin x |
|
cos (a
. x) |
– a .
sin (a . x) |
|
cos (u
(x)) |
– u’ (x)
. sin (u (x)) |
|
sin x
|
cos x |
|
sin (u
(x)) |
u’
(x) . cos (u (x)) |
|
tan x |
|
|
ln x |
|
|
ln (u (x)) |
|
|
ex |
ex |
|
eu (x) |
u’
(x) eu (x) |
|
u2 |
2 u’ . u |
|
Asin x |
|
|
Acos x |
|
|
Atan x |
|
|
xr
r
rationnel |
r
. xr
– 1 |
-
Tableau de primitives
usuelles :
|
fonction |
Primitive |
|
f
(x) |
F
(x) à
une constante près |
|
0 |
cte |
|
a |
a
. x + cte |
|
xn |
|
|
sin x
|
– cos x
+ cte |
|
sin (a
. x) |
|
|
cos x
|
sin x +
cte |
|
cos (a
. x) |
|
|
|
ln |x|
+ cte |
|
ex |
ex
+
cte |
|
|
|
|
|
|
|
Avec n
>2 |
|
|
|
|
|
u
(x) . u’ (x) |
|
|
|
ln |x|
+ cte |
|
|
|
1)- Dérivées : Trouver les dérivées des fonctions
suivantes :
|
|
Fonction |
Dérivée |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
2)- Primitives : Trouver les primitives des fonctions
suivantes :
|
|
Fonction |
Primitive |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
* |
|
7 |
|
* |
-
* :
Explications
►
Remarque :
-
Pour 6 : On utilise :
-
V
= x2
+ 3x
+ 1, il découle de ceci que V’
= 2 x +3
-
La fonction est de la
forme :
|
Fonction |
Primitive |
|
|
|
-
Pour 7 :
-
On
pose : V
= (3 x
+2), il découle de ceci que
V’ = 3
-

-
Voilà
pourquoi, il apparaît le coefficient
3,
au dénominateur, dans l’expression.
|
|