L’ensemble des nombres complexes est une extension de l’ensemble des nombres réels.

I- Les trois écritures :

1)- Le nombre imaginaire :

-  La grandeur i représente le nombre imaginaire tel que :

-  i² = – 1

-  Remarque : le carré de (– i) est aussi égal à – 1.

-  (–i)² = – 1

2)- Écriture générale :

-  z = a + i . b

-  les nombres a et b sont des nombres réels.

3)- Écriture trigonométrique :

-  z = ρ . (cos θ + i . sin θ)

-  La grandeur ρ : module du nombre complexe

-  La grandeur θ : argument du nombre complexe

-  Conséquences :

-  a = ρ . cos θ et b = ρ . sin θ

-   

-  et

-   

4)- Écriture exponentielle :

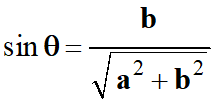
-  z = ρ . e ^{i . θ}

-  Conséquences :

-  a = ρ . cos θ et b = ρ . sin θ

-   

-  et

-   

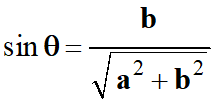
5)- Nombres complexes conjugués :

-  Le nombre complexe conjugué, de z = a + i . b, est

-  De même :

-  z = ρ . (cos θ + i . sin θ) et sont des nombres complexes conjugués

-  z = ρ . e ^{i . θ} et sont des nombres complexes conjugués.

►  Le complexe conjugué a même partie réelle, mais une partie imaginaire opposée.

-  Propriété :

-   

6)- Les fonctions trigonométriques : cosinus et sinus.

-  À partir des notations suivantes :

-  z = ρ . (cos θ + i . sin θ) et z = ρ . e ^{i . θ}

-  On tire :

-  e^{i . θ} = cos θ + i . sin θ  et  e ^{– i . θ} = cos θ – i . sin θ

-  On en déduit que :

-   

-   

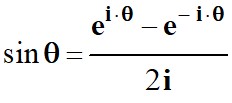
II- Utilisation pour la résolution d’une équation différentielle.

1)- Équation différentielle d’un circuit (R, L, C).

Oscillations libres dans un circuit (R, L, C).

-  Montage :

-  On utilise l’additivité des tensions :

-   

-  On pose : R = R’ + r et on ordonne :

-   

-  Durant les oscillations libres amorties, la charge q du condensateur obéit à l’équation différentielle :

-   

-  Formulation générale :

-   

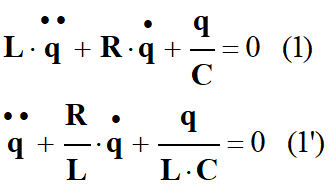
-  On pose :

-   

-  Le terme λ est lié à l’amortissement du système.

-  Le terme ω₀² est lié à la pulsation propre du système :

-  On obtient l’équation générale suivante :

-   

-  On retrouve cette forme d’équation différentielle aussi bien en mécanique qu’en électricité.

2)- Amortissement nul :

-  On se place dans le cas : λ = 0

-  On obtient l’équation différentielle suivante :

-   :

-  On recherche une solution sous la forme suivante :

-  x = A . e ^{α . t}

-  On tire, l’expression de la dérivée première :

-   

-  Et de la dérivée seconde :

-   

-  L’équation suivante doit être vérifiée ceci quel que soit x ( ∀ x)

-   

-   

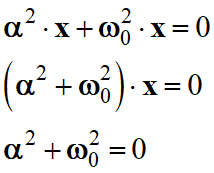
-  La solution générale est une combinaison linéaire du type :

-   

-  On fixe les conditions initiales suivantes :

-  On en déduit les relations suivantes :

-   

-   

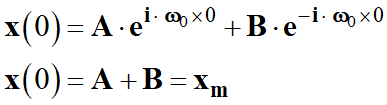
-  On en déduit l’expression de x en fonction du temps :

-   

►  Autre méthode : 

-  La solution générale est de la forme suivante :

-  x = A . (cos (ω₀ . t) + i . sin (ω₀ . t)) + B . (cos (ω₀ . t) + i . sin (ω₀ . t))

-  (A + B) . cos (ω₀ . t) + i . sin (ω₀ . t) + i . sin (ω₀ . t). (A – B)

-  Comme x est une réel :

-  (A + B) € R et  (A – B) est un imaginaire pur.

-  Les grandeurs A et B sont des complexes conjugués :

-  Avec :

-  Expression de la solution générale :

-  x = ρ . e ^{i . φ} . e ^{i . ω0 . t} + ρ . e ^{– i . φ} . e ^{– i . ω0 . t}

-      

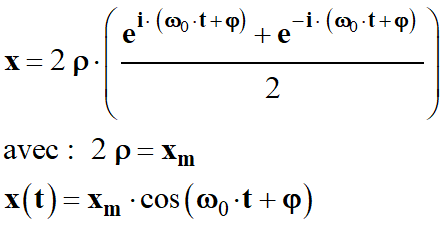
3)- L’amortissement n’est pas nul :

-  On se place dans le cas : λ ≠ 0

-  On obtient l’équation différentielle suivante :

-   :

-  On recherche une solution sous la forme suivante :

-  x = A . e ^{α . t}

-  On tire, l’expression de la dérivée première :

-   

-  Et de la dérivée seconde :

-   

-  L’équation suivante doit être vérifiée ceci quel que soit x :

-   

-  En conséquence :

-   

-  On obtient une équation du second degré en α :

-  On calcule de discriminant réduit :

-  Δ’ = λ² – ω₀²

a)-  1^ier cas : Δ’ > 0 : Régime apériodique. (λ > ω₀)

-  λ² > ω₀²

-  On est dans le cas où l’amortissement est grand.

-  On pose : λ² – ω₀² = ω²

-  L’équation admet deux solutions :

-  α’ = – λ + ω et α’’ = – λ – ω

-  La solution générale est une combinaison linéaire du type :

-   

-  Les grandeurs A et B sont liées aux conditions initiales :

-  On choisit comme conditions initiales :

-  On en déduit les relations suivantes :

-   

-  Détermination de  :

-   

-   

-  Il faut exprimer les grandeurs A et B en fonction des caractéristiques du système λ, ω et x_m.

-  Remarque : ne pas oublier que λ² – ω₀² = ω².

-   

-  On obtient la solution générale suivante :

-   

-  On peut l’écrire sous la forme suivante :

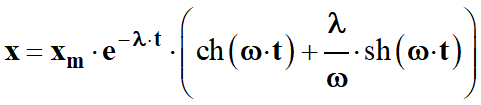-   avec λ > ω₀

-  L’amplitude du système décroit au cours du temps sans oscillations.

b)-  2^ième cas : Δ’ > 0 : λ² < ω₀² : Régime pseudo-périodique (λ < ω₀)

-  λ² – ω₀² < 0 => ω₀² – λ² >0

-  On est dans le cas où l’amortissement est faible.

-  Posons : ω² = ω₀² – λ²

-   

-  L’équation donne deux solutions imaginaires :

-  α’ = – λ + i . ω et α’’ = – λ – i . ω

-  La solution générale est une combinaison linéaire du type :

-   

-  Les grandeurs A et B sont liées aux conditions initiales :

-  On choisit comme conditions initiales :

-  On en déduit les relations suivantes :

-   

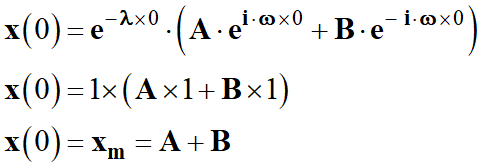
-  Détermination de   :

-   

-   

-  Il faut exprimer les grandeurs A et B en fonction des caractéristiques du système λ, ω et x_m.

-  Remarque : ne pas oublier que ω² = ω₀² – λ².

-   

-  Solution générale :

-  

-   avec λ < ω₀

-  L’amplitude du système décroit au cours du temps et on observe des oscillations.

-  On peut écrire x sous deux autres formes :

-   

-   

-  Les grandeurs x_m, φ et ϕ sont liées aux conditions initiales.

-  La grandeur x_m représente l’amplitude du système.

-  Les grandeurs φ et ϕ représentent la phase à l’instant initial.

►  Remarque :

-  Si l’amortissement λ est très faible, alors ω ≈ ω₀

-  La grandeur ω représente la pseudo-pulsation.

-  On observe un régime périodique amortie de pseudo-période ω.

c)-  3^ième cas : Δ’ > 0 : Régime critique.

-  α’ = – λ

-  La solution générale peut se mettre sous la forme suivante :

-   

-  Expression de la dérivée première :

-   

-  Expression de la dérivée seconde :

-   

-  L’équation générale est la suivante :

-   

-  On remplace  par leurs expressions respectives dans l’équation générale :

-   

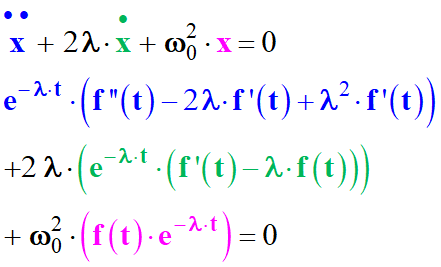
-  On tire :

-   

-  Cette équation est vérifiée, si et seulement si :

-   

-  Les constantes A et B dépendent des conditions initiales :

-  On choisit comme conditions initiales :

-  On en déduit les relations suivantes :

-   

-  Au temps t = 0 s, x (0) = x_m.

-  x (0) = x_m = A

-   

-  La fonction de x est la suivante :

-   

-  Expression de la dérivée première :

-   

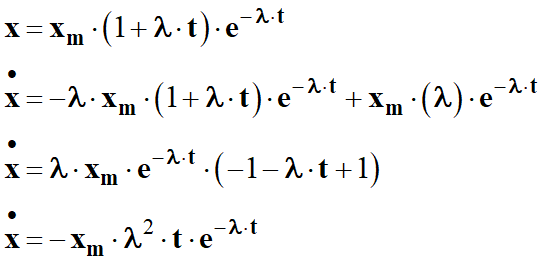
-  Le système regagne sa position d’équilibre le plus rapidement possible.

-  C’est l’amortissement critique.

III- Visualisation des différents régimes :

-  Visualisation avec le tableur Excel :

Simulation avec Excel : Oscillations libres amorties u, i,  

- Influence de la valeur de R, résistance du circuit.

-  Régime apériodique : l’amortissement est grand, R > R_C (résistance critique) : On choisit : R = 350 Ω

-  Régime pseudo-périodique :

-  Si l’amortissement est faible ( R = 1 Ω), la valeur de la pseudo-pulsation est proche de la période propre.

-  ω ≈ ω₀

-  Si l’amortissement est nul ( R = 0 Ω) , on observe des oscillations libres :

-  Régime critique : R = R_C (résistance critique)

Animation : https://phyanim.sciences.univ-nantes.fr/Meca/Oscillateurs/Oscillat1_FJ.php

►  Exemple de l’oscillateur mécanique horizontal :

Oscillateur mécanique horizontal : Le pendule élastique

-  Schéma :

Osillateur mécanique amorti (Exercice)

ou

Vidéo :

-  Régime pseudo-périodique :

Amination :

-  Régime apériodique :

-  Régime critique :