Le dipôle RL, La bobine, cours de physique de terminale S, ts07ph

Pour aller plus loin :

Mots clés :

La bobine ; établissement du courant dans une bobine ;

induction ; auto-induction ; circuit RL ;

constante de temps d'un circuit RL,

énergie emmagasinée dans une bobine ; l'alternateur ; ...

I- La bobine.

- Une bobine est constituée d’un enroulement de fil conducteur, recouvert d’un vernis isolant, sur un cylindre de rayon r.

- On désigne par ℓ la longueur de l’enroulement et par r le rayon d’une spire :

- Si L est petit devant r, la bobine est plate.

- Si L est voisin de r la bobine est appelée : solénoïde.

- Si L est plus grand que 10 r, le solénoïde est dit infini..

II- Influence d’une bobine dans un circuit. (TP Physique N° 08)

- Expérience : Retard à l’établissement du courant.

- Montage 1 :

- Observations : La lampe L₂ s'allume avec un retard sur la lampe L₁.

- Il se produit un retard à l'établissement du courant dans la portion de circuit qui comporte la bobine.

- Une bobine s’oppose transitoirement à l’établissement du courant dans un circuit.

- En régime permanent, la bobine se comporte comme un conducteur ohmique de résistance r.

III- Caractéristiques d’une bobine.

1)- L’inductance d’une bobine.

- Une bobine est un dipôle, de bornes A et B, caractérisé par son inductance L exprimée en henry (symbole H).

- On utilise souvent le millihenry ( mH).

- L'inductance L de la bobine est une constante positive qui ne dépend que des caractéristiques géométriques de la bobine

- pour une bobine de longueur ℓ, qui possède N spires de surface S.

2)- Résistance d’une bobine.

- En régime permanent, la bobine se comporte comme un conducteur ohmique de résistance r.

- Une bobine est aussi caractérisée par sa résistance r qui s’exprime en ohm (W).

3)- Représentation symbolique d’une bobine.

4)- Expression de la tension aux bornes d’une bobine.

- Une bobine est caractérisée par son inductance L et sa résistance r.

- La bobine étant orientée de A vers B, la tension u_AB aux bornes de la bobine est donnée par la relation :

Tension aux bornes d’une bobine : u_ABtension en volt (V)

u _AB = L .	di

	dt

r . i

{

I intensité en ampère (A)

r résistance en ohm (Ω)

L inductance en henry (H)

- Remarque : cas d’une bobine idéale (r = 0)

u _AB = L .	di

	dt

- On peut aussi utiliser cette écriture si r << R (résistance du circuit).

IV- Établissement du courant dans une bobine. (TP Physique N° 08).

1)- Étude expérimentale : Réponse à un échelon de tension.

- Montage 2 : réponse d’une bobine à un échelon de tension.

- Il comprend :

- Un générateur idéal de tension E = 3,2 V ;

- un conducteur ohmique de résistance R’= 18 Ω,

- une bobine d’inductance L et de résistance r = 8,8 Ω et

- un interrupteur K.

- Au temps t = 0 s, on ferme l’interrupteur en le basculant sur la position 1.

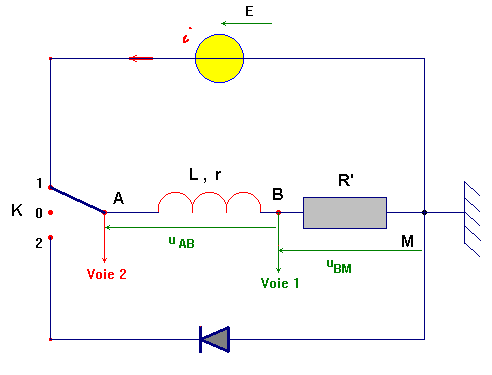
- Que visualise-t-on à la voie 1 de la carte CANDIBUS ?

- On visualise les variations de la tension aux bornes du conducteur ohmique, c'est-à-dire la tension u_BM.

- Si l'on considère qu'au temps t, le courant circule dans le sens positif choisi,

u _BM =
	R' . i

i =	1

	R'

. u _BM

- On visualise les variations de l'intensité en fonction du temps, ceci à une constante près.

- Observations : On pose : R = r + R’

- La tension aux bornes du dipôle (R, L) passe brutalement de la valeur à la valeur E = 3,2 V.

- L’intensité traversant le circuit est nulle juste après la fermeture de l’interrupteur K,

- puis elle augmente progressivement jusqu’à atteindre une valeur maximale et reste constante.

- Le courant met environ la durée Δt ≈ 8,0 ms pour s’établir.

- Premier temps : t

- t € [ t₀, t₀+ Δt] : régime transitoire, établissement du courant dans la bobine.

- t € [ t₀+ Δt, t₁ ] : régime permanent, le courant est établi.

- La bobine s'oppose à l'établissement du courant dans le circuit.

2)- Équation différentielle vérifiée par l’intensité i.

- On ferme l’interrupteur.

- On oriente le circuit et on étudie le dipôle (R, L).

- La loi d’additivité des tensions dans le circuit série permet d’écrire :

E = u _AB + u _BM

E =(L .

+ r . i) +

R' . i

- En ordonnant, on peut écrire :

E = L .	di

	dt

( r + R'). i

En posant R = r + R'

E = L .	di

	dt

R . i (1)

- On reconnaît une équation différentielle du premier ordre avec deuxième membre qui admet une solution du type :

- i (t) = A . e^k.t + B où A, B et k sont des constantes.

3)- Détermination des constantes.

- On détermine les constantes à l’aide des conditions initiales et des paramètres du circuit.

- Première étape : on reporte l’expression de la solution dans l’équation (1).

- La relation (2) est vérifiée à chaque instant.

- Or E = c^te, R . B = c^te et t et par conséquence e^k.t varient au cours du temps.

- Il faut nécessairement que :

{

(L . k + R ) . A = 0

{

k = –	R

	L

E = R . B

La solution A = 0 n'a pas de signification physique

- Conditions initiales : au temps t = 0 s, l’intensité dans le circuit est nulle : i (0) = 0.

- On déduit de ceci que :

i (0) = A .e ^{k .}⁰ + B = 0

A + B = 0

A = – B = –	E

	R

- Relation donnant l’intensité traversant le dipôle (R, L) soumis à un échelon de tension E :

- Expression de la tension aux bornes de la bobine en fonction du temps.

- On peut en déduire l’expression de la tension aux bornes de la bobine :

- étude de la relation :

- Quelle est la valeur de la tension aux bornes de la bobine au temps t = 0 s ?

- u _AB = E.

- Quelle est la valeur de l’intensité dans le circuit lorsque t tend vers l’infini ?

i (∞) = I

	E

	R

V- Rupture du courant dans un circuit.

1)- Expériences.

- Montage 1 : visualisation du phénomène à l'oscilloscope.

- Il comprend :

- Un G.B.F qui délivre une tension carrée f = 1000 Hz

- Un conducteur ohmique de résistance R₁ réglable de 0 à 500 Ω.

- Une bobine d'inductance L = 20 mH et de résistance r = 20 Ω.

- Un conducteur ohmique de résistance R = 18 Ω.

- Que visualise-t-on à la voie A de l'oscilloscope ?

- On visualise les variations de la tension aux bornes du G.B.F, c'est-à-dire la tension u_AM.

- Que visualise-t-on à la voie B de l'oscilloscope ?

- On visualise les variations de la tension aux bornes du conducteur ohmique de résistance R₁, c'est-à-dire la tension u_BM.

- Si l'on considère qu'au temps t, le courant circule dans le sens positif choisi

u _BM =
	R₁ . i

i =	1

	R₁

. u _BM

- On visualise les variations de l'intensité en fonction du temps, ceci à une constante près.

- Observations :

- La courbe qui apparaît à la voie B, ne suit pas exactement les variations de celle qui apparaît à la voie A.

- Il y a un retard à l'établissement et à l'annulation du courant dans le circuit

2)- Interprétation.

- Premier temps :

- t € [ t₀, t₀ + Δt] : régime transitoire, établissement du courant dans la bobine.

- t € [ t₀ + Δt, t₁ ] : régime permanent, le courant est établi.

- La bobine s'oppose à l'établissement du courant dans le circuit.

- Deuxième temps :

- t € [ t₁, t₁ + Δt] : régime transitoire, établissement du courant dans la bobine.

- t € [ t₁ + Δt, t₂ ] : régime permanent, le courant est établi.

- La bobine s'oppose à l'annulation du courant dans le circuit.

- La bobine s’oppose à la diminution de l’intensité du courant électrique dans le circuit.

3)- Équation différentielle vérifiée par l’intensité i lors de l’ouverture du circuit.

- L’interrupteur étant sur la position 1, on le bascule sur la position 2.

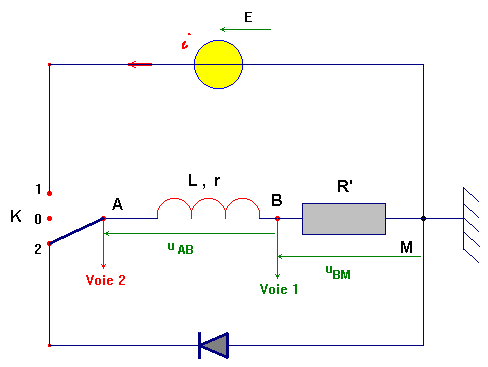
- On oriente la partie du circuit qui nous intéresse :

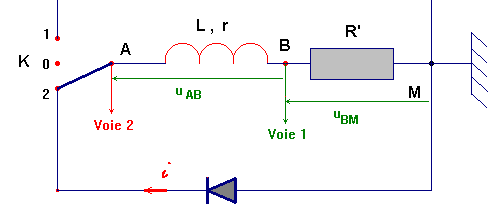
- D’après la loi d’additivité des tensions dans un circuit série, on a l’égalité :

u _AB + u _BM = 0

E =(L .

+ r . i) +

R' . i
	= 0

L .	di

	dt

( r + R'). i

= 0

En posant R = r + R'

L .	di

	dt

R . i = 0 (1)

- On reconnaît une équation différentielle du premier ordre en i sans deuxième membre.

- Elle admet une solution du type : i (t) = A . e^k.t + B où A, B et k sont des constantes.

- On détermine les constantes à l’aide des conditions initiales et des paramètres du circuit.

- Il découle de la relation que :

- Il faut nécessairement que :

{

(L . k + R ) . A = 0

{

k = –	R

	L

0 = R . B

B = 0

La solution A = 0 n'a pas de signification physique

- Condition initiale : au temps t = 0 s, L’interrupteur est en position 1.

- Le courant est établi est l’intensité dans le circuit est donnée par la relation :

i (0) =	E

	R

- On déduit de ceci que :

i (0) = A .e ^{k .}⁰ + B =	E	=>	A + B =

	R

A =	E

	R

- L’intensité du courant électrique i traversant le dipôle (R, L) a pour expression :

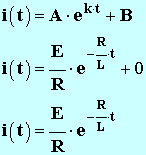
- Remarque :

- Lorsque t tend vers l’infini, alors i (t) tend vers zéro.

- Le courant électrique ne s’annule pas brusquement à l’ouverture du circuit.

- La bobine s’oppose à la diminution de l’intensité du courant électrique dans le circuit.

- De façon générale, une bobine s’oppose aux variations de l’intensité du courant électrique dans un circuit.

- Expression de la tension aux bornes de la bobine en fonction du temps.

- On peut en déduire l’expression de la tension aux bornes de la bobine :

- En utilisant le fait que : R = r + R’ :

- Quelle est la valeur de la tension aux bornes de la bobine au temps t = 0 s ?

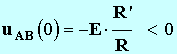- , elle est négative.

- La bobine se comporte comme un générateur de f.é.m .

- Quelle est la valeur de l’intensité dans le circuit lorsque t = 0 s?

i (0) = I =	E

	R

- Lorsque le temps t tend vers l’infini, i (∞) = 0 et u _AB (∞) = 0.

- L'intensité dans le circuit ne subit pas de discontinuité.

VI- Constante de temps du circuit.

1)- Expression de la constante de temps τ.

- La durée de l’établissement ou de l’annulation du courant dans un circuit (R, L) dépend de la résistance R et de l’inductance L du circuit.

- On appelle constante de temps du circuit (R, L), la valeur :

τ =	L

	R

- τ constante de temps : seconde s.

- R résistance du circuit ohm W.

- L inductance du circuit : henry H.

- Lors de l’établissement du courant, l’expression de l’intensité du courant électrique dans le circuit est donnée par l’expression :

- Lors de l’annulation du courant électrique dans le circuit :

2)- Analyse dimensionnelle :

- D’autre part de la relation : , on tire que :

- En combinant (1) et (2) :

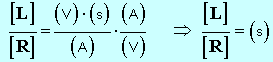
- Le rapport a la dimension d’un temps.

- Il s’exprime en seconde dans le S.I.

3)- Détermination de la constante de temps τ.

- Pour déterminer graphiquement la valeur de τ, on trace la tangente à l’origine à la courbe i = f (t) et l’asymptote horizontale à cette courbe.

- L’abscisse du point d’intersection de ces deux droites donne la valeur de la constante de temps τ.

- D’après la relation :

- Pour t = τ :

- Pour t = 5 τ :

VII- Énergie emmagasinée dans une bobine.

1)- Expériences : Étincelle de rupture moteur avec bobine et noyau de fer doux.

- Montage :

- Les étincelles de rupture montrent que l'énergie emmagasinée dans la bobine est libérée brutalement lors de l'ouverture du circuit.

- L'étincelle correspond à la conduction de l'air.

- Si le stylet est distant de 0,1 mm, alors : | e | ≈ 300 V et le champ électrique E ≈ 300000 V / m, potentiel disruptif de l'air sec.

2)- Expression de l'énergie emmagasinée dans une bobine.

- Une bobine d'inductance L, traversée par un courant d’intensité i, emmagasine de l'énergie. C'est de l'énergie magnétique que l'on note E_m ou W_L.

E_m énergie en joule (J)

E_m = W_L=

L . i ²

L inductance en henry (H)

I intensité en ampère (A)

- L’intensité du courant électrique dans un circuit comportant une bobine ne subit pas de discontinuité.

- Le courant s’établit de façon progressive et s’annule de la même façon.

- L’intensité du courant électrique ne peut pas passer de façon instantanée de la valeur zéro à la valeur I.

VIII- Applications.

1)- QCM :

QCM Réalisé avec le logiciel Questy

Pour s'auto-évaluer

Le circuit (R, L)

Sous forme de tableau

QCM Réalisé avec le logiciel Questy

Pour s'auto-évaluer

Le condensateur, la bobine et la résistance, Circuit (RC), circuit (LC) et circuit (RLC)

2)- Exercices :

1)- Exercice 9 page 188.	2)- Exercice 12 page 189.
3)- Exercice 13 page 189.	4)- Exercice 21 page 190.
5)- Exercice 23 page 192.
Bac Blanc : Une équation au service des sciences physiques