TP Physique N° 08 bis, Etabblissement du courant dans une bobine, énoncé, terminale S, tstp08ph4

Mettre en évidence le retard à l'établissement du courant et le phénomène d'auto-induction dû à une bobine dans un circuit.

Détermination de la valeur de l'inductance propre d'une bobine par différentes méthodes.

II- Le logiciel.

1)- Mise en place.

- Cliquer sur l'icône WinLabo2

- Sélectionner : Ouvrir une nouvelle page et 8 (clic gauche).

2)- Préparation de l'acquisition :

Étape N° 1

puis 8 (clic gauche).

Étape N° 2

puis (clic gauche).

puis sur OK

Étape N° 3

Nombre de points :

400

Intervalle de temps

entre deux mesures :

40 ms

puis (clic gauche).

puis sur Annuler.

III- Expérience.

1)- Montage :

- Faire le schéma normalisé du montage, le réaliser et le faire vérifier.

Schéma normalisé :

2)- Acquisition :

- Régler valeur de la tension aux bornes du générateur E = 3,2 V.

- Dans l'expérience réalisée, E = 3,23 V.

- Réaliser l'acquisition :

Étape N° 5

(clic gauche) sur Acquisition,

puis Réglages.

puis (clic gauche).

puis sur OK.

- Fermer l'interrupteur K en le basculant sur la position 1.

- Sauver les mesures : nom du fichier : AUTOTS4

3)- Rappels et compléments.

a)- Loi d'ohm aux bornes d'un conducteur ohmique : R représente la résistance du conducteur ohmique.

u _AB = R.I

b)- Loi d'ohm aux bornes d'une bobine : L représente l'inductance propre de la bobine et r la résistance de la bobine.

L'unité d'inductance L

est le henry de symbole H.

IV- Exploitation et Mesures.

1)- Étude quantitative de la courbe : u_BM = g(t)

a)- Visualisation de u_BM = g (t) :

- On utilise l'ordinateur pour enregistrer le phénomène transitoire qui est très bref.

Cliquer sur l’icône

Mettre t en abscisses (X)

Et U1 en ordonnées (Y)

et sur OK.

- Donner un titre au graphe obtenu :

puis	Pour le titre du graphe taper : u _BM = g(t) et sur OK

- Que représente la courbe obtenue ?

- Expliquer qualitativement cette courbe.

- Montrer qu'il existe deux phases.

- Donner les limites de chaque phase.

- Qualifier chacune des phases.

- Quelle est la durée Δt₁ de la première phase ?

- Courbe expérimentale obtenue :

b)- Déduire de la courbe la valeur maximale de la tension U₀ aux bornes du conducteur ohmique lorsque le régime permanent est atteint.

- On peut utiliser les curseurs :

Choix des Curseurs :

puis

puis déplacer les lignes bleues.

- Pour affiner la mesure, on peut utiliser la loupe . Pour retrouver l’affichage initial, sur .

c)- Déterminer la valeur de la tension U_0L aux bornes de la bobine lorsque le régime permanent est atteint.

d)- Donner la durée Δt au bout de laquelle 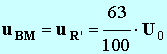. Que représente Δt ?

2)- Étude de la courbe : i = f (t)

- Calcul de la valeur de l’intensité au cours du temps. Placer le curseur dans la colonne C.

Cliquer sur Variable,

Puis Ajouter

Taper la formule :

U1/18

et sur OK

a)- Visualisation de la courbe : i_exp = h (t)

Cliquer sur l’icône

Mettre t en abscisses (X)

Et i en ordonnées (Y)

et sur OK.

- Donner un titre au graphique : i_exp= h (t)

- Modifier le motif : (droit avec la souris sur le graphe),

- Choisir la couleur de fond (rouge) et la couleur de ligne (rouge).

b)- Déterminer la valeur du courant I₀ dans le circuit lorsque le régime permanent est atteint.

c)- Donner l'expression littérale de la loi d'ohm aux bornes de la bobine et aux bornes du conducteur ohmique.

d)- Que peut-on dire de la valeur de lorsque le régime permanent est atteint ? En déduire la valeur de la résistance totale R du circuit. Comparer R et r + R' . Conclusion.

e)- Sachant que la constante de temps du circuit (R, L) : 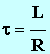et que d'autre part t = Δt : voir la question : (IV-1)-d)), calculer la valeur de l'inductance propre L de la bobine.

3)- Étude de .

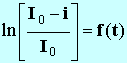Pour tracer cette courbe, on va utiliser l'ordinateur :

- Donner la valeur de I₀, arrondir cette valeur par excès au mA supérieur. On note I_ex la valeur obtenue.

a)- Saisie de la formule :

- On remplace I₀ par I_ex au numérateur car autrement un message d’erreur s’affiche lorsque i = I₀.

- entrer les valeurs de I_ex et de I₀. Si un message d'erreur apparaît : augmenter la valeur de I_ex.

- Placer le curseur dans la colonne D.

Cliquer sur Variable,

Puis Ajouter.

Taper la formule :

ln((I _ex –i)/ I ₀

Dans cet exemple,

I _ex = 0,137 A

I ₀ = 0,136 A

et sur OK

b)- Visualisation de la courbe .

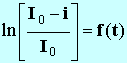Cliquer sur l’icône

Mettre t en abscisses (X)

Et ln en ordonnées (Y)

et sur OK.

c)- Exploitation de la courbe obtenue.

- Quelles sont les caractéristiques de la courbe obtenue ?

- Montrer que . Déterminer la valeur de a' à l'aide du pointeur.

- Indiquer le signe de a' et son unité.

- En déduire la valeur de τ , con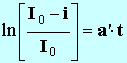stante positive telle que : .

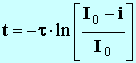- Donner l'unité de τ.

- Sachant que 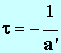et que 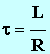, calculer l'inductance propre L de la bobine.

- En déduire :

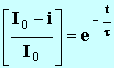
- et enfin i = h (t) .

4)- Vérification à l'ordinateur : tracé de la courbe i_th = h₁ (t) à l'ordinateur

- Saisie de la formule : pour I₀ et τ, on tape les valeurs trouvées.

- Placer le curseur dans la colonne E.

Cliquer sur Variable,

Puis Ajouter .

Taper la formule :

I ₀ * (1-exp(-t/t))

Dans cet exemple,

I ₀ = 0,136 A

t = 0,00161 s

et sur OK

- Afficher les courbes i_exp= h (t) et i_th= h₁ (t) sur le même graphique et comparer.

- Remarques. Conclusions.

- On peut faire un décalage de Δt' pour que les deux courbes se superposent.

- Déterminer Δt' à l'aide des curseurs et dans la formule, remplacer t par t + Δt .

V- Étude complémentaire. (si le temps le permet)

- Donner l'expression de 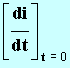en fonction de I₀ et τ.

- Tracer la tangente à la courbe à t = 0. Tracer l’asymptote horizontale.

- Donner les coordonnées du point d’intersections. Pour affiner les mesures, on peut utiliser la loupe .

- sur puis sur le point O (0, 0) du graphique i _th= h ₁(t) pour avoir la tangente à l’origine

- sur puis sur l’extrémité de la courbe pour avoir l’asymptote horizontale.

- En déduire la valeur de la constante de temps τ du circuit.

- En déduire la valeur de L.

- Comparer les différentes valeurs de L trouvées par les différentes méthodes.

- Conclusions.