Pour aller plus loin : 

I-  Exercice 14 page 61.

On réalise la courbe d’absorbance d’une solution de permanganate de potassium dans une cuve d’épaisseur 1 cm.

On obtient les résultats suivants :

1)- Tracer la droite d’étalonnage A = f (C).

Cliquer sur l'image pour l'agrandir

-  De la droite d’étalonnage, on peut déduire que :

-  A (λ) = k . C

-  A (λ) = 2,25 x 10 ³ . C

2)- En déduire la valeur du coefficient d’absorption molaire de l’ion permanganate.

-  ε (λ) est appelé coefficient d’extinction molaire ou coefficient d’absorption molaire.

-   Il dépend de la nature de l’espèce dissoute et de la longueur d’onde de la radiation utilisée.

-   Il dépend également du solvant et de la température. (mol ^{– 1}.L.cm ^{– 1}).

-   

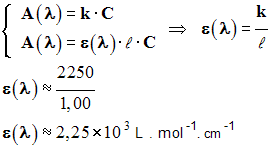
-   Pour vérifier, on peut avec le tableur Excel, tracer la courbe de tendance et demander, l'équation de la courbe et le coefficient de détermination R².

3)- Une solution de concentration C inconnue présente une absorbance égale à 0,500. Déterminer C en mol / L.

-   On peut faire une lecture graphique ou un calcul.

-   Lecture graphique :

Cliquer sur l'image pour l'agrandir  

-  Calcul :  

-  

II- Exercice 16 page 62.

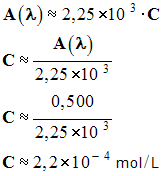
-  Graphe de [ I₂ ] en fonction de t :

Cliquer sur l'image pour l'agrandir  

1)- Déterminer la concentration en ions iodure à l’instant t = 0.

-  Concentration initiale en ions iodure.

-  On mélange :

-  V₂ = 70 mL d’eau oxygénée de concentration C₂ = 2,0 × 10 ^{– 1}  mol / L.

-  V₁ = 20 mL d’iodure de potassium de concentration C₁ = 5,0 × 10 ^{– 2}  mol / L.

-  V₃ = 10 mL d’acide sulfurique de concentration C₃ = 5,0 × 10 ^{– 1}  mol / L..

-         

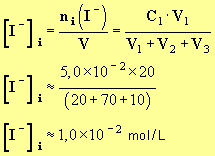
2)- Définir la vitesse volumique de réaction.

3)- Déterminer graphiquement la valeur de la vitesse v₀ en mol / L / s.

-  Le graphe :

Cliquer sur l'image pour l'agrandir  

-  La valeur de la vitesse au temps t = 0 est donnée par la valeur du coefficient directeur k de la tangente T₀.

4)- Quelle est la valeur du temps de demi-réaction ?

-  Valeur du temps de demi-réaction.

-  Le temps de demi-réaction, noté t_1/2, est la durée au bout de laquelle l’avancement de la réaction est égal à la moitié de sa valeur finale.

-  Le temps de demi-réaction est atteint lorsque l’avancement de la réaction est égal à la moitié de l’avancement final.

-  Tableau d’avancement de la réaction :

-  Si :

-  

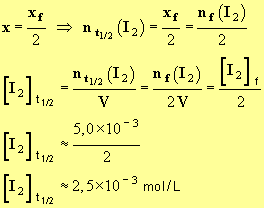
Cliquer sur l'image pour l'agrandir

-  Graphiquement, on trouve que : t_1/2 ≈ 2 min.

-  Le temps de demi-réaction fournit une échelle des temps caractéristique du système étudié.

-  On peut considérer que la réaction est pratiquement terminée au bout de 8 min.

III- Exercice 18 page 62.

On introduit une masse m = 1,00 g de zinc en poudre dans un ballon contenant un volume V₁ = 40,0 mL d’acide chlorhydrique de concentration C₁ = 0,500 mol / L.

On recueille le gaz dihydrogène formé au cours du temps et on mesure son volume V.

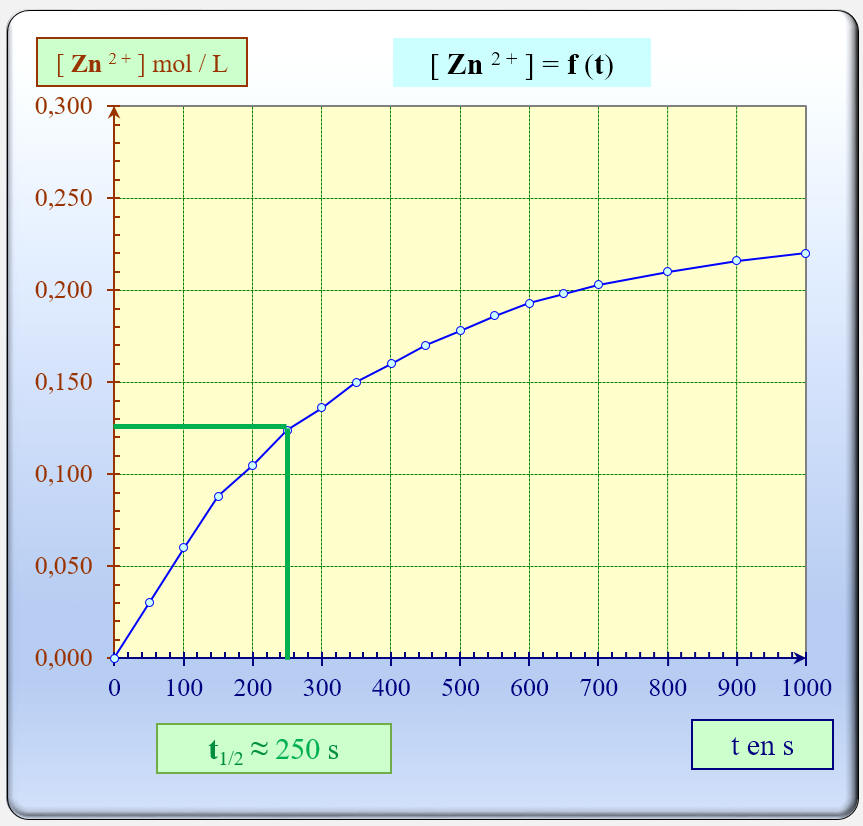
L’ensemble des résultats de cette expérience permet de tracer le graphe représentant les variations de la concentration en ions Zn ²⁺ en fonction du temps.

 Cliquer sur l'image pour l'agrandir

-  Donnée : le volume molaire dans les conditions de l’expérience est V_m = 24,0 L.mol ^{– 1} .

1)- Écrire l’équation de la réaction d’oxydoréduction se produisant entre les couples : H ⁺ _(aq) / H_{2 (g)}  et Zn ²⁺ _(aq) / Zn  _(s)

2)- Quelle est la relation entre la concentration en ions zinc II et le volume de dihydrogène formé ?

-  On peut travailler avec le tableau d’avancement de la ré action.

-  À chaque instant :

- 

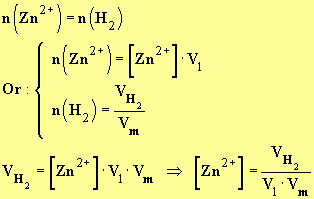
-  Valeur de la concentration :

-  

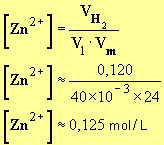
3)- Définir la vitesse volumique de la réaction.

Déterminer les valeurs de v aux dates t = 0 s, 300 s, 600 s et 1000 s.

-  Valeur de la vitesse t = 0 s.

 Cliquer sur l'image pour l'agrandir

-  La valeur de la vitesse au temps t = 0 est donnée par la valeur du coefficient directeur k de la tangente T₀.

-  Valeur de la vitesse t = 300 s.

Cliquer sur l'image pour l'agrandir

-  Valeur de la vitesse t = 600 s.

Cliquer sur l'image pour l'agrandir

-  Valeur de la vitesse t = 1000 s.

Cliquer sur l'image pour l'agrandir

4)- Comment évolue la vitesse au cours du temps ? Justifier.

-  La vitesse volumique de réaction diminue au cours du temps.

-  La courbe tend vers une asymptote horizontale et le coefficient directeur de la tangente à la courbe tend vers zéro.

5)- Quel est le réactif limitant ? Quelle est la valeur de la concentration en ions zinc II quand t tend vers l’infini ?

-  Le réactif limitant : On travaille avec une partie du tableau d’avancement.

-   La réaction est finie par manque d’un des réactifs : en conséquence, il faut résoudre :

-  Valeur de la concentration en Zn²⁺.

-  En fin de réaction, on peut considérer que tous les ions H ⁺ ont réagi.

-  D‘après le bilan de quantité de matière de l’équation de la réaction : 

-  Avec : x_max  = 1,00 × 10 ^{– 2} mol

-  

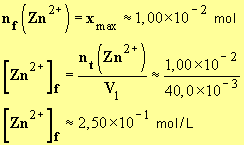
6)- En déduire le temps de demi-réaction.

-  Temps de demi-réaction : il est atteint lorsque :

- 

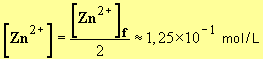
 Cliquer sur l'image pour l'agrandir

-  La lecture graphique donne : t_1/2 = 250 s.

IV- Exercice 24 page 64.

 Préparation des Solutions.

1)- Masse de peroxodisulfate d’ammonium nécessaire.

-  On donne :

-  volume de la solution : V = 100 mL

-  concentration de la solution C = 1,0 × 10 ^–1 mol / L.

-  Masse molaire du peroxodisulfate d’ammonium :

-  M ((NH₄)₂S₂O ₈) = M = 18,0 x 2 + 32,1 x 2 + 16,0 x 8

-  M ((NH₄)₂S₂O₈) = M ≈ 228 g / mol

-  Équation de dissolution : Par définition : 

-  En conséquence :

-  La concentration en soluté est : C,

-  La concentration en ions ammonium est :

-  [NH₄ ⁺]  = 2 C  

-   La concentration en ions peroxodisulfate est : 

-  [S₂O₈ ^{2 –}] = C

-  Quantité de matière utilisée : n = C . V

-  Masse de peroxodisulfate nécessaire : m = n . M = C . V . M

-  Application numérique :

-  m = C . V . M

-  m = 1,0 x 10 ^{– 1} x 0,100 x 228

-  m ≈  2,3 g

2)- Préparation de la solution S’.

-          Il s’agit d’une dilution :

-          Au cours de la dilution, il y a conservation de la quantité de matière de soluté :

-  Matériel nécessaire : fiole jaugée de 100 mL et pipette jaugée de 20 mL avec sa propipette.

-  On verse 25 mL de solution d’iodure de potassium dans un bécher.

-  On prélève 20 mL à l’aide de la pipette munie de sa propipette.

-  On les verse dans une fiole jaugée de 100 mL.

-   On ajoute de l’eau distillée ( 3 /4).

-   On mélange puis on ajoute de l’eau distillée jusqu’au trait de jauge et on homogénéise.

 étude de la réaction.

1)- Concentration molaire volumique en ions S₂O₈ ^{2 –} à t = 0.

-          On a mélangé 100 mL de solution S avec 100 mL de solution S’.

-         

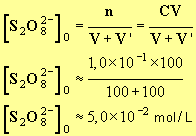
2)-  

a)-     On refroidit pour arrêter la réaction à la date t. La température est un facteur cinétique.

b)-     Relation entre n (I₂) et n (S₂O₃^{2 –}).

-          On utilise une solution titrée de thiosulfate de sodium de concentration C₂ = 1,0 × 10 ^{– 2} mol / L.

-         A l’équivalence, le volume de solution de thiosulfate de sodium est V₂. 

-  Relation à l’équivalence : n (S₂O₃^{2 –}) – 2 x _max = 0  et n (I₂) – x _max = 0

-  Cette relation permet de déterminer la quantité de matière de diiode présente dans le volume V₀ à partir de la quantité de matière d’ions thiosulfate versé. 

-  On peut écrire : 

-  n (S₂O₃ ^{2 –}) = 2 n_t (I₂)

c)- relation donnant la concentration de I₂ dans chaque prélèvement de volume V₁.

-  

-  

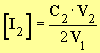
3)- tracé du graphe :

 Cliquer sur l'image pour l'agrandir

4)-  

a)- Vitesse volumique de la réaction.

b)- Valeur de la vitesse aux dates t = 20 min et t = 40 min.

-  La définition donne : 

-    

-  La vitesse volumique de la réaction correspond à la dérivée par rapport au temps de la concentration en diiode par rapport au temps.

-  Sachant que , on utilise le graphe   [I₂] _t = f (t)  

-  La vitesse volumique de la réaction à la date t₁ = 20 min est égale au coefficient directeur de la tangente à la courbe C au point M₁ d’abscisse t₁.

Cliquer sur l'image pour l'agrandir

-  La vitesse volumique de la réaction à la date t₂ = 40 min est égale au coefficient directeur de la tangente à la courbe C au point M₂ d’abscisse t₂.

Cliquer sur l'image pour l'agrandir

c)- Au cours du temps, la vitesse de la réaction diminue pour s’annuler lorsque la réaction est finie.