I- Le vecteur vitesse.

1)- Vitesse moyenne d'un point mobile.

a)-  Définition.

-  La vitesse moyenne d'un point mobile est égale au quotient de la distance parcourue par la durée du parcours.

-  Relation :

-  Dans le S.I, l'unité de vitesse est le mètre par seconde.

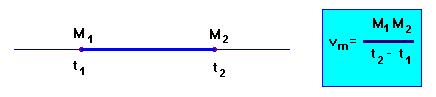
b)-  Cas d'un mouvement rectiligne.

c)-  Cas d'un mouvement curviligne.

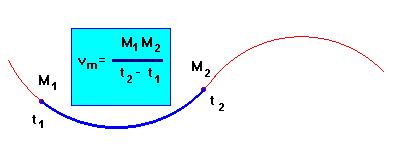
2)- Vitesse d'un point mobile.

-  C'est la vitesse à un instant donné. C'est la vitesse donnée par le tachymètre à l'instant ou on le regarde.

-  On définit cette vitesse afin de mieux décrire le mouvement d'un point mobile.

-  On ne sait calculer qu'une vitesse moyenne.

-  On va considérer que pendant un intervalle de temps très court, la vitesse ne varie pratiquement pas et qu'elle reste pratiquement constante.

-  On peut en conséquence utiliser la relation précédente.

-  La vitesse instantanée v (t) d’un point mobile, à la date t, est pratiquement égale à sa vitesse moyenne calculée pendant un intervalle de temps très court encadrant l’instant t considéré.

-  Remarque 1 :

-  La valeur donnée par cette relation est d'autant plus proche de la vraie valeur que la durée Δt = t" - t' est petite.

-  Lorsque la durée Δt devient très petite, on la note τ.

-  Remarque 2 :

-  Il faut toujours préciser le référentiel étude pour déterminer la valeur de la vitesse.

-  La vitesse est relative au référentiel d'étude.

-  Remarque 3 :

-  La valeur de la vitesse mesurée par un radar est la valeur instantanée de la vitesse.

-  Remarque 4 :

-  Lorsque la valeur de la vitesse d’un point mobile :

-  Reste constante au cours du temps, le mouvement de ce point mobile est uniforme.

-  Augmente au cours du temps, le mouvement est accéléré.

-  Diminue au cours du temps, le mouvement est décéléré ou retardé.

3)- Le vecteur vitesse.

a)-  Valeur du vecteur vitesse.

-  Le système étudié est considéré comme ponctuel : c’est un point mobile.

-  Dans un référentiel donné, la valeur v_i de la vitesse du système dans la position M_i est assimilée à la valeur de la vitesse moyenne du système entre deux positions très proches M_i et M_i+1.

-  Expression :

-   

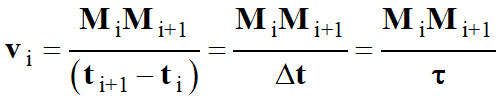
-  Schéma :

-  Le terme M_iM_i+1 représente la longueur du segment [M_iM_i+1] en mètre (m).

-  Le terme Δt = (t_{i + 1} – t_i) = τ représente la durée très courte du parcours entre les deux positions très proches M_i et M_i+1.

b)-  Caractéristiques du vecteur vitesse.

-  Le vecteur vitesse  , au point M_i de la trajectoire,  est assimilé au vecteur vitesse moyenne obtenu pour une durée Δt = (t_{i + 1} – t_i) extrêmement courte :

-   

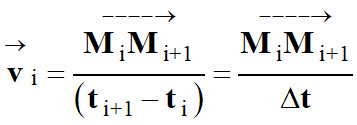
-  Le vecteur vitesse  a les caractéristiques suivantes :

-  Origine : position occupée par le point mobile à l'instant considéré t_i.

-  Direction : tangente à la trajectoire au point considéré.

-  Sens : celui du mouvement à cet instant

-  Valeur : celle de la vitesse à cet instant :

-   

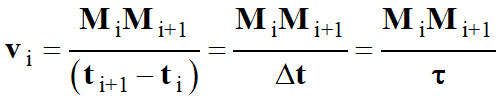
c)-  Représentation du vecteur vitesse  :

-  On représente le vecteur vitesse par un segment fléché :

-  Vecteur vitesse du point mobile M_i à l'instant t_i que l'on note plus simplement.

-  Pour tracer ce vecteur vitesse :

-  Origine : position occupée par le point mobile à l'instant considéré t_i c'est-à-dire le point M_i .

-  Direction : tangente à la trajectoire au point considéré : droite parallèle à (M_i–1 M_i+1) issue de M_i.

-  Sens : celui du mouvement à cet instant

-  Valeur : celle de la vitesse à cet instant :

-   

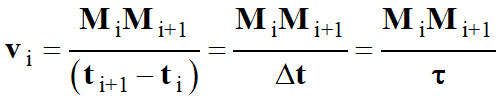
-  Longueur du représentant ℓ_v :

-  Une échelle de représentation est indispensable.

-  Elle associe la longueur du segment fléché à la valeur de la vitesse.

-  Échelle : 1 cm ↔ 0,1 m / s.

-  Exemple :

-  Dans le cas présent, on a enregistré la position du point mobile M, à intervalles de temps égaux très courts :  τ = 40 ms.

-  On veut tracer le vecteur vitesse  au temps t₃.

-  Pendant cette durée, le mobile parcourt la distance M₃M₄ ≈ 1,28 cm

-  Valeur de la vitesse v₃ :

- 

-  Le segment fléché aura une longueur : ℓ_v3  = 3,2 cm.

II- Le vecteur variation de vitesse.

1)- Introduction :

-  Lors d’un mouvement, le vecteur vitesse  d’un système peut varier

-   En direction

-  En sens

-  Ou en valeur.

   Expérience 1 :

-  Un mobile autoporteur est placé sur une table à digitaliser horizontale.

-  À l’instant t = 0 s, on lâche le mobile autoporteur.

-  Il est entraîné dans son mouvement par la masse marquée qui est accrochée au fil.

-  On enregistre la position du centre d’inertie G du solide à intervalles de temps égaux τ.

-  Ceci est possible grâce à la table à digitaliser munie de son stylet.

-  L’ordinateur enregistre la position du stylet à intervalle de temps régulier τ (très court).

-  La configuration choisie permet de sélectionner une vingtaine de points.

-  Le document obtenu est à l’échelle 1.

-  Schémas 

Expérience 1

  Expérience 1  enregistrement

-  Enregistrement : On obtient l’enregistrement suivant.

-  m₁ = m₂ = 100 g et τ = 20 ms

-  Bilan des forces.

-  Le mobile est soumis à son poids , la réaction du support  et la tension du fil .

-  Schéma :

-  Conséquence : , le solide n’est ni isolé, ni pseudo-isolé.

-  La résultante des forces extérieures appliquées au solide est différente du vecteur nul :

-   

-  On remarque que le vecteur vitesse du centre d’Inertie  garde la même direction et le même sens au cours du mouvement.

-  Par contre, la valeur de la vitesse change au cours du mouvement

- (le point mobile parcourt des distances de plus en plus grandes pendant des durées égales).

-  Il découle de ceci que le vecteur  varie au cours du mouvement.

b)-  Expérience 2 :

-  Le mobile autoporteur, maintenu par un fil tendu, est lancé sur la table à digitaliser.

-  La table est horizontale.

-  On enregistre la position du centre d’inertie du solide à intervalles de temps égaux τ après avoir lâché le mobile.

Expérience 2

Vidéo

-  Enregistrement : On obtient l’enregistrement suivant.

-  Bilan des forces.

-  Le mobile est soumis à son poids , la réaction du support  et la tension du fil .

-  Schéma :

-  Conclusions :

-  Conséquence :, le solide n’est ni isolé, ni pseudo-isolé.

-  La résultante des forces extérieures appliquée au solide est différente du vecteur nul :

-  On remarque que le vecteur vitesse du centre d’Inertie  garde la même valeur.

-  Par contre, la direction du vecteur vitesse change au cours du mouvement.

-  En conséquence le vecteur  varie au cours du mouvement.

2)- Le vecteur variation de vitesse.

a)-  Définition.

-  Lors d’un mouvement, le vecteur vitesse  d’un système peut varier en direction, en sens ou en valeur.

-  Le vecteur variation de vitesse  n’est alors pas égal au vecteur nul.

-   Le vecteur variation de vitesse  d’un système en mouvement entre deux positions M_i et M_j est défini par :

-   

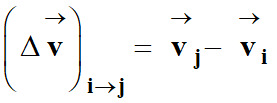
b)-  Étude de l’expérience 1 :

-  Intervalle de temps : τ = 20,0 ms

-  Valeur de la masse m : m = 100 g

-  Enregistrement :

-  Vitesse du point mobile au point A :

-  AB ≈ 1,45 cm et Δt = 20 ms

-   

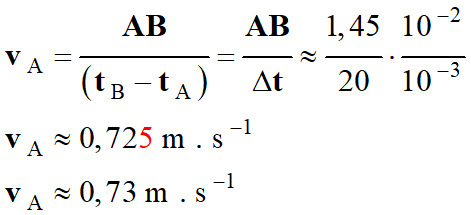
-  Tracé du vecteur

Échelle pour la vitesse : 1 cm ↔ 0,2 m . s^–1

ℓ_vA ≈ 3,6 cm

-  Vitesse du point mobile au point B :

-  BC ≈ 1,32 cm et Δt = 20 ms

-   

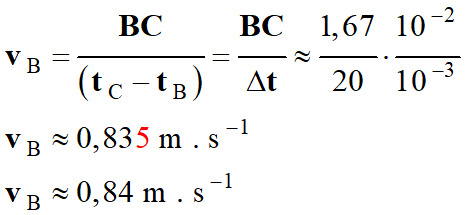
-  Tracé du vecteur

Échelle pour la vitesse : 1 cm ↔ 0,2 m . s^–1

ℓ_vB ≈ 4,2 cm

-  Vecteur variation de vitesse :

-  Tracé du vecteur : L’origine du vecteur est le point B.

-  Longueur du représentant de :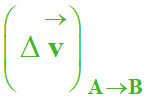

-  ℓ_Δv ≈ 0,60 cm

-  Valeur du vecteur variation de vitesse :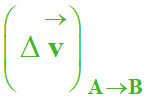

-  (Δv)_A→B ≈ 0,12 m . s^–1

-  Remarques :

-  Les vecteurs vitesses  et  ont :

-  Même direction

-  Même sens

-  Mais des valeurs différentes.

-  Le mouvement est rectiligne accéléré.

-  Le mobile parcourt des distances de plus en plus grandes pendant des durées égales.

-  Les points sont alignés.

-  Le vecteur variation de vitesse  a même direction que le fil qui tient le mobile.

-   Il a même direction et même sens que la tension du fil .

-  Il a même direction et même sens que .

c)-  Étude de l’expérience 2 :

-  Intervalle de temps : τ = 40,0 ms

-  Enregistrement :

-  Vitesse du point mobile au point A :

-  Mesure avec Word :

-  AB ≈ 2,0 cm et Δt = 40 ms

-   

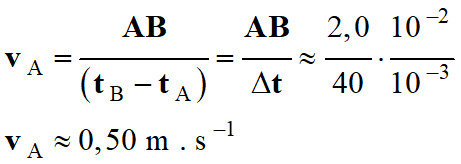
-  Tracé du vecteur

Échelle pour la vitesse : 1 cm ↔ 0,1 m . s^–1

ℓ_vA ≈ 5,0 cm

-  Vitesse du point mobile au point B :

-  BC ≈ 2,0 cm et Δt = 40 ms

- 

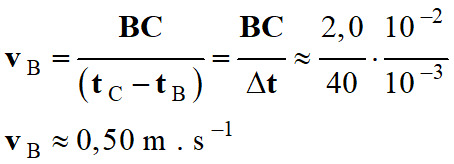
-  Tracé du vecteur

Échelle pour la vitesse : 1 cm ↔ 0,1 m . s^–1

ℓ_vB ≈ 5,0 cm

-  Vecteur variation de vitesse :

-  Tracé du vecteur : L’origine du vecteur est le point B.

-  Longueur du représentant de :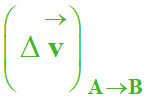

-  ℓ_Δv ≈ 1,4 cm

-  Valeur du vecteur variation de vitesse :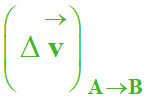

-  (Δv)_A→B ≈ 0,14 m . s^–1

-  Remarques :

-  Les vecteurs vitesses  et  ont :

-  Des directions différentes

-  Mais la même valeur.

-  Le mobile parcourt des distances égales pendant des durées égales.

-  Le mobile est animé d’un mouvement circulaire uniforme.

-  Le vecteur variation de vitesse  a même direction que le fil qui tient le mobile.

-   Il a même direction et même sens que la tension du fil .

-  Il a même direction et même sens que .

III- La somme des forces appliquées au système.

1)- Introduction.

-  Une action mécanique exercée par l’extérieur sur le système étudié est modélisée par une force .

-  Cette force est représentée par un segment fléché, appelé vecteur force noté :

-  Caractéristiques :

-  L’origine : point d’application de la force, point où l’on considère que la force s’exerce.

-  La direction : Celle de la droite d’action de la force

-  Le sens : celui de la force.

-  La valeur de la force.

-  L’unité de force est le newton (N).

-  Lorsque la valeur de la force est connue, la longueur du segment fléché est proportionnelle à cette valeur.

-  Pour ce faire, on utilise une échelle de représentation :

-  Exemple : 1 cm ↔ 1 N

2)- Contraposée du principe d’inertie :

-  Énoncé 1 :

-  Énoncé 2 :

-  Réciproque de la contraposée du principe d’Inertie :

3)- Deuxième loi de Newton.

-  Dans un référentiel donné, si un système de masse m constante est soumis à une ou plusieurs forces constantes,

le vecteur variation de vitesse  de ce système pendant une durée très courte Δt et la somme de ces forces sont reliés par la relation :

-  Ces deux vecteurs sont colinéaires.

-  La somme vectorielle des forces qui s’exercent sur un système  est également appelée résultante des forces notée :

-   

4)- Le rôle de la masse du système.

-  D’après la relation approchée :

-   

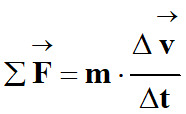
-  Plus la masse d’un système est grande et plus il est difficile de modifier le mouvement de ce système.

-  Pour deux systèmes de masses différentes, il faut exercer sur le système de plus grande masse une somme des forces de plus grande valeur afin d’obtenir la même variation de vitesse .

-  Si on exerce la même somme des forces  sur deux systèmes de masses différentes, plus la masse du système est grande, plus la valeur du vecteur variation de vitesse est petite.

IV- Applications.

1)- Mouvement de chute libre avec vitesse initiale (séance de travaux pratiques).

a)-  Protocole expérimental.

Les logiciels : Virtualdub – aviméca 2.7 – Excel.

Parabil Parabil.zip

-  Vidéo :PARABILLE

-  Une balle de masse m est lancée d'un point G₁ avec une vitesse initiale faisant un angle α avec l'horizontale.

-  Une étude chronophotographique permet d’étudier le mouvement de la bille dans un référentiel terrestre.

-  La WebCam est située dans un plan perpendiculaire à l’axe de visée.

-  Ouvrir le logiciel d’acquisition et de traitement vidéo : aviméca 2.7.

-  Clique sur l’icône :  et dans le dossier vidéo, choisir le fichier Parabille.

-  Choisir comme échelle de la vidéo : 200 % pour plus de précision.

-  Repérer les différentes positions de la bille au cours de son mouvement.

-  Cliquer sur l’icône Étalonnages :

b)- traitement des résultats.

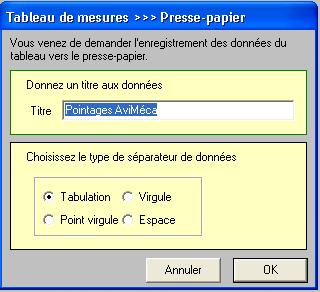
Cliquer sur l’icône :  . Il apparaît l’affichage ci-contre : Cliquer sur OK. Les valeurs sont dans le presse-papier. Il ne reste plus qu’à les exploiter

-  Le logiciel : EXCEL.

-  Ouvrir un fichier Excel

-  Sélectionner coller. On obtient l’affichage suivant :

-  Tableau de valeurs :

-  Propriétés du clip :

-  Étude chronophotographique :

-  Étude avec AVIMECA 2.7 : pointage des différentes positions de la balle.

-  Le système est soumis à son poids :

-  D’après la réciproque de la contraposée de principe d’Inertie :

-  Sur l’enregistrement, on remarque que le vecteur vitesse change de direction et de valeur à chaque instant.

-  Lorsque la balle monte, la valeur de la vitesse diminue et lorsque la balle descend la valeur de la vitesse augmente.

-  Vecteur variation de vitesse :

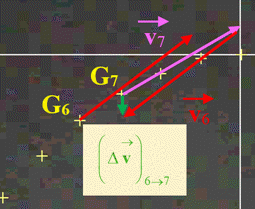
-  Le tracé du vecteur variation de vitesse :

-  Tracer 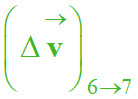 et

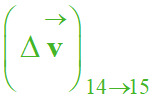
-  Tableau simplifié des valeurs  :

-  Échelle : 1 cm ↔ 1 m . s^–1

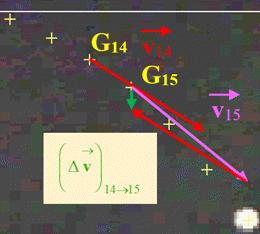
Et

-  Remarques :

-  ℓ_Δv6→7 ≈ ℓ_Δv14→15 ≈ 0,38 cm

-  On en déduit que :

-  Δv_6→7 ≈ Δv_14→15  ≈ 0,38 m . s^–1.

-  Le vecteur variation de vitesse garde la même valeur au cours du mouvement.

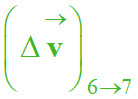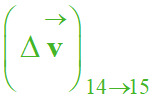-  D’autre part , les vecteurs  et  ont :

-  même direction est même sens que le vecteur poids .

2)- QCM.

QCM réalisé avec le logiciel QUESTY

Pour s'auto-évaluer

 Le vecteur vitesse

le vecteur variation de vitesse

La somme des forces appliquées au système

Sous forme de tableau

3)- Exercices.

 

Exercices : DS 1)- Exercice 01 page 234 :Tracer un vecteur vitesse. 2)- Exercice 04 page 234 : Tracer un vecteur variation de vitesse. 3)- Exercice 06 page 235 : Connaître la direction et le sens de 4)- Exercice 07 page 235 : Exploiter la somme des forces. 5)- Exercice 08 page 235 : Connaître l’influence de la masse du système. 6)- Exercice 10 page 236 : Planeur au décollage. 7)- Exercice 16 page 237 :  L’attraction gravitationnelle du Soleil. 8)- Exercice 18 page 238 : Une Histoire de pointage. 9)- Exercice 22 page 239 : Ski de vitesse. 10)- DS N° 01 :Exercice 25 page 240 : Stand up paddle. (40 min)