|
Mouvements d'un système |
|
|
|
|
|
|
QCM N° 12
Le vecteur
vitesse
Le vecteur
variation de vitesse
La somme des
forces appliquées au système
Le rôle de la
masse du système
Pour chaque
question, indiquer la (ou les) bonne(s) réponse(s). |
|||||
|
|
Énoncé |
A |
B |
C |
R |
|
1 |
Le vecteur
vitesse
position P2
a pour valeur : |
|
|
|
A |
|
2 |
Le vecteur
vitesse
|
Égal à 4 cm |
Représenté par
un segment
fléché de
4 cm. |
Égal à 4 cm . s–1 |
B |
|
3 |
Le vecteur
variation de vitesse
M2
et M3 de la trajectoire non rectiligne
d’un système : |
Est parallèle à
la trajectoire |
Est tangent à
la trajectoire |
A pour direction
celle de
|
C |
|
4 |
Pour un
mouvement circulaire uniforme d’un
système : |
La valeur
du vecteur
vitesse est
constante |
Le vecteur
variation de
vitesse est
égal au
vecteur nul |
Le vecteur
variation de
vitesse n’est
pas égal au
vecteur nul. |
AC |
|
5 |
Pour un
système de masse m constante et
soumis à une ou plusieurs
forces, on a la relation
approchée : |
|
|
|
BC |
|
6 |
Lors du
mouvement d’un système, une
représentation correcte de
|
|
|
|
C |
|
7 |
Un système a
une masse m constante. Si
la valeur de la somme des
forces appliquées au système
diminue : |
La valeur du
vecteur variation
de vitesse du
système diminue
proportionnellement |
La valeur du
vecteur variation
de vitesse du
système augmente
proportionnellement |
La valeur du
vecteur variation
de vitesse du
système ne
change pas. |
A |
|
8 |
Un système est
soumis à des forces dont la
valeur de la somme Si la masse
m du système diminue :
|
Pour une valeur
Δt,
la valeur du
vecteur variation
de vitesse
diminue. |
Pour une valeur
Δt,
la valeur du
vecteur variation
de vitesse
ne change pas. |
Pour une valeur
Δt,
la valeur du
vecteur variation
de vitesse
augmente. |
C |
|
9 |
Une balle
jaune et une noire plus lourde
ont, pendant la même durée Δt, le même vecteur
la somme sur la balle
jaune est : |
Plus grande que
celle de
la somme
des forces
s’exerçant sur
la balle noire. |
égale à celle
de la somme
des forces
s’exerçant sur
la balle noire. |
Plus petite que
celle de la
somme
des forces
s’exerçant sur
la balle noire. |
C |
QCM réalisé avec le logiciel Questy
Pour s’auto-évaluer
Vitesse moyenne d'un point mobile :
-
La vitesse moyenne
d'un point mobile est égale au quotient de la distance parcourue par la durée du
parcours.
-
Relation :
|
|
Vitesse moyenne
vmoy
en m . s–1 |
|
Distance parcourue : d en
m |
|
|
Durée du parcours : Δt en
s |
-
Dans le
S.I, l'unité de
vitesse est le mètre par seconde.
Valeur du vecteur vitesse.
-
Le système étudié est
considéré comme ponctuel : c’est un point mobile.
-
Dans un
référentiel donné, la valeur
vi de
la vitesse du système dans la position
Mi
est assimilée à la valeur de la vitesse moyenne du système entre deux positions
très proches Mi
et Mi+1.
-
Expression :
-
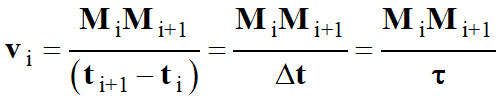
-
Le
terme MiMi+1
représente la longueur du segment [MiMi+1]
en mètre (m).
-
Le
terme Δt
= (ti
+ 1 –
ti) =
τ représente la durée très
courte du parcours entre les deux positions très proches
Mi
et Mi+1.
Le vecteur vitesse :
-
Le vecteur vitesse
![]() ,
au point Mi
de la trajectoire,
est assimilé au vecteur vitesse
moyenne obtenu pour une durée
Δt = (ti + 1
– ti)
extrêmement courte :
,
au point Mi
de la trajectoire,
est assimilé au vecteur vitesse
moyenne obtenu pour une durée
Δt = (ti + 1
– ti)
extrêmement courte :
-
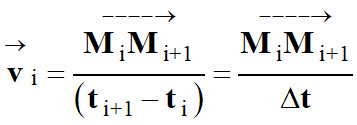
-
Le vecteur vitesse ![]() a
les caractéristiques suivantes :
a
les caractéristiques suivantes :
-
Origine : position occupée par le point mobile
à l'instant considéré ti.
-
Direction : tangente à la trajectoire au point
considéré.
-
Sens
: celui du mouvement à cet instant
-
Valeur : celle de la vitesse à cet instant :
-
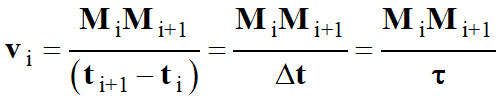
-
Représentation du
vecteur vitesse
![]() :
:
-
On représente le
vecteur vitesse par un segment fléché grâce à une échelle de représentation.
Le vecteur variation de vitesse :
-
Le vecteur variation
de vitesse
![]() d’un
système en mouvement entre deux positions
Mi
et Mj
est défini par :
d’un
système en mouvement entre deux positions
Mi
et Mj
est défini par :
-
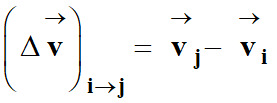

-
Le vecteur variation
de vitesse a
même direction et même sens que
![]() .
.
Contraposée du principe
d’inertie :
-
Énoncé 1 :
|
Lorsque, entre deux
instants voisins, le vecteur vitesse
alors les forces
qui s’exercent sur ce système ne se compensent pas. |
-
Énoncé 2 :
|
Lorsqu’un
système n’est ni immobile, ni en mouvement rectiligne uniforme
(ni
alors les forces qui s’exercent sur
ce système ne se compensent pas : |
-
Réciproque de la
contraposée du principe d’Inertie :
|
Réciproquement, lorsque les forces qui s’exercent sur un système ne se compensent pas ( ( |
Deuxième loi de Newton.
- Dans un référentiel donné, si un système de masse m constante est soumis à une ou plusieurs forces constantes,
le vecteur variation
de vitesse
![]() de
ce système pendant une durée très courte
Δt
et la somme de ces forces sont reliés par la relation :
de
ce système pendant une durée très courte
Δt
et la somme de ces forces sont reliés par la relation :
|
|
Valeur de la
force F en newton (N) |
|
Valeur de la
masse m en kilogramme (kg) |
|
|
Valeur de la
durée Δt en seconde (s) |
-
Ces deux vecteurs sont
colinéaires.
Le rôle de la masse du système.
-
D’après la relation
approchée :
-
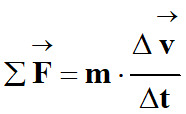
-
Plus la
masse m d’un système est grande et
plus il est difficile de modifier le mouvement de ce système.
-
Pour deux système de
masses différentes, il faut exercer sur le système de plus grande masse une
somme des forces
![]() de plus grande valeur afin d’obtenir la même variation de
vitesse.
de plus grande valeur afin d’obtenir la même variation de
vitesse.
-
Si on exerce la même
somme des forces
![]() sur
deux systèmes de masses différentes, plus la masse du système est grande, plus
la valeur du vecteur variation de vitesse est petite.
sur
deux systèmes de masses différentes, plus la masse du système est grande, plus
la valeur du vecteur variation de vitesse est petite.
|
|