Programme 2011 : Phys. N° 01 Vision et images. Programme 2011 : Physique et Chimie Programme 2020 : Physique et Chimie

Pour aller plus loin :

I- Rappels et compléments.

1)- Propagation de la lumière.

- La lumière n’a pas besoin de milieu matériel pour se propager.

- La lumière se propage en ligne droite dans un milieu transparent homogène.

- Chaque point d’une source de lumière envoie de la lumière dans toutes les directions suivant des droites.

- On utilise le modèle du rayon lumineux.

- Il donne la direction de propagation de la lumière ainsi que le sens de propagation.

- Un faisceau lumineux est un ensemble de rayon lumineux (le rayon lumineux n’existe pas).

- On distingue : le faisceau parallèle, convergent et divergent.

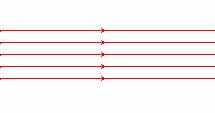
Faisceau parallèle

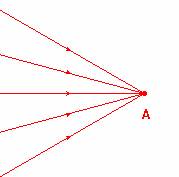
Faisceau convergent

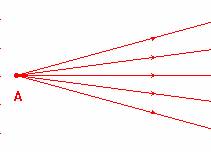
Faisceau divergent

- La lumière se propage dans le vide avec une célérité :

-  c = 3,00 x 10⁸ m/s.

- La longueur d'onde dans le vide d'une onde lumineuse est la distance qu'elle parcourt, dans le vide, pendant une durée égale à une période T.

-  On la note  λ₀.

- Relation fondamentale :

 -   

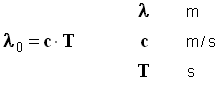
- ou 

- Remarque : pour la lumière, on utilise la lettre n pour la fréquence au lieu de f.

- Relation :  

- La longueur d'onde d'une radiation lumineuse dépend du milieu de propagation.

- 

- Vitesse de propagation de la lumière dans le milieu considéré.

- En déduire une relation simple entre λ et λ₀ .

- Relation :   

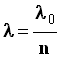
- La longueur d’onde de la lumière dépend du milieu de propagation.

-  La fréquence f ne dépend pas du milieu de propagation.

2)- Réflexion et réfraction de la lumière.

- Loi de la Réflexion :  i₁ =  r

- Loi de la Réfraction  : n₁ . sin i₁ =  n₂ . sin i₂ .

animation

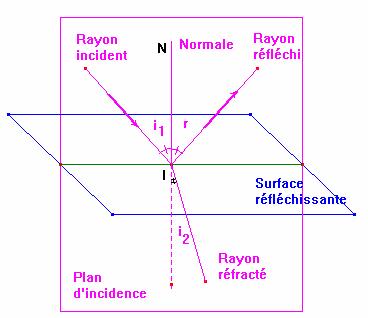
II- Description des lentilles minces.

1)- Définitions

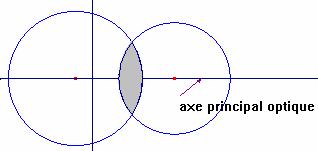
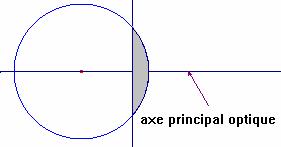
- Une lentille mince est un milieu transparent solide (verre, quartz, …) limité par deux calottes sphériques ou par une calotte sphérique et un plan.

- L’axe qui joint les centres des 2 sphères est un axe de symétrie pour la lentille. On l’appelle l’axe principal optique.

- Une lentille est dite mince si son épaisseur e mesurée sur son axe est très petite devant les rayons de courbure de ses faces.

2)- Classification des lentilles minces.

a)-  Les lentilles à bords minces : les lentilles convergentes.

b)-  Les lentilles à bords épais : les lentilles divergentes.

3)- Représentation symbolique des lentilles minces.

a)- Les lentilles minces convergentes :

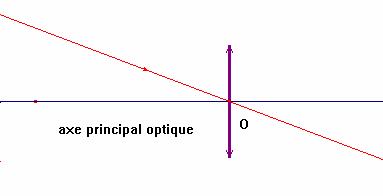
-  Le centre optique est le point où l’axe principal optique traverse la lentille. On le note toujours O.

- Tout rayon lumineux qui frappe la lentille à son centre optique la traverse sans déviation.

b)- Les lentilles minces divergentes :

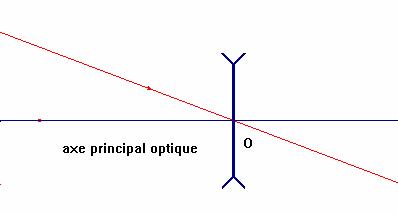
4)- Notion d’objet et d’image.

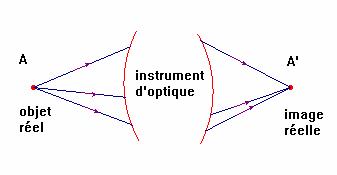
a)- Objet réel et image réelle :

- un point objet est réel s’il est le sommet d’un faisceau lumineux divergent qui va frapper l’instrument d’optique.

- Un point image est réel s’il est le sommet d’un faisceau lumineux qui émerge de l’instrument d’optique en convergeant.

b)- Objet réel et image virtuelle :

- Un point image est virtuel s’il est le sommet d’un faisceau lumineux qui émerge de l’appareil en divergeant.

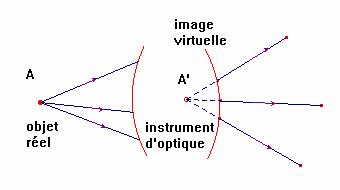
- L’œil placé derrière l’instrument voit les images virtuelles.

c)- Objet virtuel et image réelle :

- Un point objet est virtuel s’il est le sommet d’un faisceau lumineux qui entre dans l’appareil en convergeant.

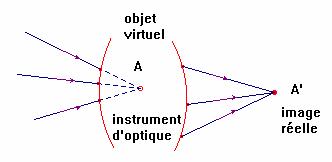
- Remarque : si les rayons passent effectivement par le point considéré celui-ci est réel.

- Si ce sont les prolongements des rayons qui passent par ce point, alors il est virtuel.

- Exemple du miroir :

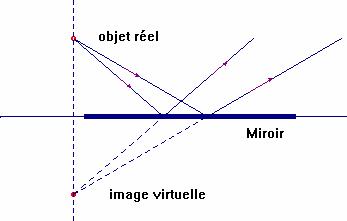
III- Conditions d’obtention d’images nettes : conditions de Gauss.

1)- Notion de stigmatisme.

- Un système optique est rigoureusement stigmatique s’il donne, d’un point objet A, un point image A’.

- Le miroir plan est un exemple de système optique rigoureusement stigmatique.

- En ce qui concerne les lentilles, le stigmatisme ne peut être qu’approché. L’image d’un point est une petite tache lumineuse.

2)- Conditions de Gauss.

- Ce sont les conditions à respecter pour obtenir des images de qualité correcte (stigmatisme approché) en utilisant des lentilles minces.

- Les rayons lumineux doivent faire un petit angle avec l’axe principal de la lentille (axe optique).

- Les rayons lumineux doivent rencontrer la lentille au voisinage de son centre optique.

3)- Réalisation.

-  L’objet AB est petit et il est situé au voisinage de l‘axe optique.

-  L’objet AB est vu du centre optique sous un angle α petit α < 10 °.

- La lentille est diaphragmée.

-  Il faut que le diamètre d d’ouverture de la lentille soit petit.

- Il résulte de ceci que tout rayon lumineux issu d’un point objet traverse la lentille au voisinage de son centre optique

- et que tout rayon lumineux est peu incliné sur son axe principal.

- La lentille est alors utilisée dans les conditions de Gauss. On a réalisé un stigmatisme approché.

IV- Étude des lentilles convergentes.

1)- Propriété du centre optique.

- Un rayon lumineux passant par le centre optique ne subit aucune déviation.

- Représentation symbolique.

2)- Foyer image et distance focale.

- Tout rayon incident parallèle à l’axe principal d’une lentille convergente en émerge en passant par le point F’ appelé foyer - image de la lentille.

- Le plan focal image est le plan perpendiculaire à l’axe principal en F’.

- On choisit sur l’axe principal comme sens positif, le sens de propagation de la lumière.

- Le point F’ est situé après la lentille.

- La grandeur algébrique représente la distance focale image.

- Dans le cas d’une lentille convergente, f’ est une grandeur positive.

- Le foyer image F’ est un point réel.

3)- Foyer - objet.

- La loi du retour inverse de la lumière permet de dire que tout rayon passant par F, symétrique de F’ par rapport au centre optique O émerge parallèlement à l’axe principal.

- Le point F est appelé le foyer - objet, ce point est réel.

-  Il est situé en avant de la lentille.

- Le plan perpendiculaire à l’axe principal en F est appelé plan focal objet.

4)- Plans focaux.

- Application 1 :

-  Un faisceau parallèle arrive sur une lentille convergente.

- Un rayon de ce faisceau fait l’angle  α = 8,0° avec l’axe principal (optique).

- Représenter le faisceau qui émerge de la lentille.

- Quelles sont ses caractéristiques ?

- On peut faire la construction avec les valeurs suivantes :

- Données : diamètre de la lentille : 6 cm

- Distance focale :

- Réponse :

- On distingue le plan focal image et le plan focal objet.

- Tout faisceau parallèle arrivant sur la lentille convergente, converge en un point du plan focal image (il faut que les conditions de Gauss soient respectées).

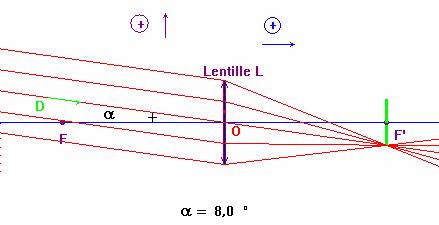
- Application 2 :

-  Un faisceau parallèle émerge d’une lentille convergente en faisant un angle d’environ 9 ° avec l’axe optique.

- D’où provient ce faisceau. Faire un schéma.

-  Réponse :

-  Tout faisceau de lumière convergeant issu d’un point du plan focal objet donne un faisceau parallèle en émergeant de la lentille.

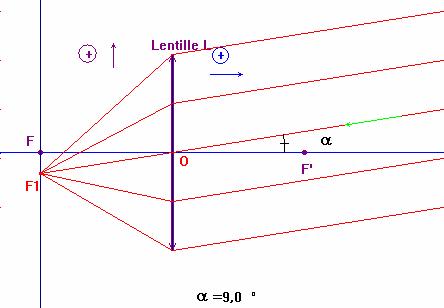
V- Image d’un objet dans une lentille convergente mince.

1)- Généralités.

- L’objet est toujours noté AB. Le point A est situé sur l’axe principal et le point B est tel que AB est perpendiculaire à l’axe principal.

- L’objet AB se situe dans un plan de front.

- Méthode générale :

- On cherche l’image du point B en considérant 2 ou 3 rayons particuliers issus du point B.

- L’image B’ du point B est l’intersection, après traversé de la lentille des rayons qui proviennent du point B.

2)- Image d’un objet réel situé en avant du foyer - objet F.

- Application 3 :

- Données : diamètre de la lentille : 6 cm

- Distance focale :

- L’objet est perpendiculaire à l’axe optique.

- Distance de l’objet au foyer - objet : et taille de l’objet : AB = 1 cm.

- Réaliser la construction.

-  Rayon 1 : issu du point B et passant par le centre optique : il n’est pas dévié.

- Rayon 2 : issu du point B et parallèle à l’axe optique. Il émerge de la lentille en passant par le point F’ foyer - image.

- Rayon 3 : issu du point B et passant par F (foyer - objet). Il émerge de la lentille parallèlement à l’axe optique.

- Les trois rayons se coupent en B’ image de B. L’image A’ de A est la projection orthogonale de B’ sur l’axe principal.

- L’objet AB est réel et l’image A’B’ est réelle et renversée.

- Utilisation de cabri géomètre : fichier : lentilleconv.fig

3)- Image d’un objet réel situé entre O et F.

- Application 4 :

- Données : diamètre de la lentille : 6 cm

- Distance focale :

- Distance de l’objet au foyer - objet : et taille de l’objet : AB = 1 cm.

- Réaliser la construction.

- Ce sont les prolongements des rayons 1, 2 et 3 qui se coupent en B’. 

- Le point B’ est l’image virtuelle du point B (elle est dessinée en pointillés).

- Pour obtenir l’image A’ du point A, on projette le point B sur l’axe optique.

- Remarques : l’image A’B’ est virtuelle et de même sens que l’objet.

- On remarque : A’B’ > AB. L’image est plus grande que l’objet. Cette lentille fonctionne en loupe.

- L’image est virtuelle.

- Elle ne se forme pas sur un écran mais elle peut être vue par l’œil à travers le système optique.

- Il faut placer l’œil sur le chemin des rayons lumineux qui émergent du système optique.

4)- Conclusions.

- La position de l’image est liée à la position de l’objet par rapport à la lentille et à la distance focale de la lentille.

- Les images peuvent être réelles ou virtuelles.

- Les images peuvent être de même sens que l’objet ou renversées par rapport à l’objet.

- Il est nécessaire d’orienter l’axe perpendiculaire à l’axe optique et passant par le centre optique.

- On l’oriente vers le haut.

Représentation :

5)- Relation de conjugaison.

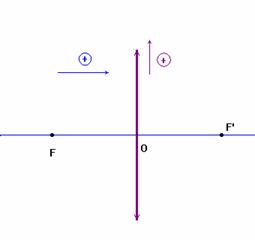
- Application 5 :

- Construire l’image A’B’, de l’objet AB, donnée par une lentille convergente.

- Données : diamètre de la lentille : 6 cm

- Distance focale :

- L’objet est perpendiculaire à l’axe optique.

- Distance de l’objet au foyer - objet : et taille de l’objet : AB = 1 cm.

- Formule de conjugaison pour les lentilles minces :

- 

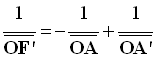
- Formule de Descartes : on pose

- 

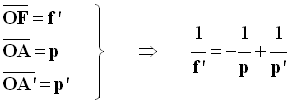
- Retrouver cette relation en utilisant le fait que les triangles OBA et OB’A’ d’une part et HOF’ et B’A’F’ d’autre part sont homothétiques (Thalès).

- Remarque : H est la projection orthogonale de B sur la lentille.

-  Les triangles OBA et OB’A’ sont homothétiques, d’après Thalès :

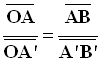-  (1)

- Les triangles HOF’ et B’A’F’ sont homothétiques, d’après Thalès :

- 

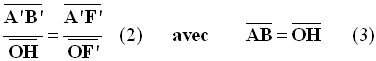
- en combinant (1), (2) et (3), il vient :

- 

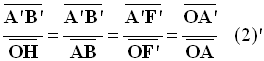
- En utilisant le fait que :

- 

6)- Vergence d’une lentille.

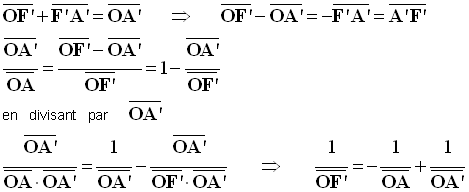
- La vergence C d’une lentille mince est l’inverse de sa distance focale image f’.

- Elle s’exprime en dioptries, symbole δ.

- La vergence est une grandeur algébrique.

-  Les lentilles convergentes ont une vergence positive.

- Les lentilles divergentes ont une vergence négative.

- 

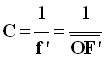
- exemple : calculer la vergence d’une lentille dont la distance focale image f’ = 2 cm.

- C = 50 δ.

7)- Grandissement.

- Le grandissement d’une lentille est donné par la relation :

- 

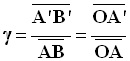
-  Si γ  >  0 l’image a le même sens que l’objet, on dit qu’elle est droite.

- Si γ  <  0  l’image est de sens contraire à l’objet, on dit qu’elle est renversée.

- Si | γ | > 1 , l’image est plus grande que l’objet et si | γ | < 1  , l’image est plus petite que l’objet.

VI- Applications.

1)- QCM :

2)- Exercices :