|
TP physique N° 11 |
Chute verticale dans un fluide : tableau de valeurs et courbes. Correction. |
|
Tableau de valeurs.
|
|
|
Programme 2012 : Physique et Chimie
Programme 2018 : Physique et chimie
|
Relevé des mesures avec AviMéca
Fichier Excel : methode_euler_eleves
Pas du calcul : δt = 30 ms
|
date
exp |
v
exp |
date
|
δv /
δt
|
v
Euler 1 |
δv /
δt
|
v
Euler 2 |
|
(
s ) |
(
m / s ) |
(
s ) |
(
m / s² ) |
(
m / s ) |
(
m / s² ) |
(
m / s ) |
|
|
|
|
|
|
|
|
|
0 |
0,000 |
0,000 |
8,61E+00 |
0,000 |
8,61E+00 |
0,000 |
|
0,02 |
0,204 |
0,030 |
6,27E+00 |
0,258 |
7,97E+00 |
0,258 |
|
0,04 |
0,369 |
0,060 |
4,56E+00 |
0,446 |
6,25E+00 |
0,497 |
|
0,06 |
0,469 |
0,090 |
3,32E+00 |
0,583 |
4,13E+00 |
0,685 |
|
0,08 |
0,585 |
0,120 |
2,42E+00 |
0,683 |
2,37E+00 |
0,809 |
|
0,1 |
0,660 |
0,150 |
1,76E+00 |
0,756 |
1,22E+00 |
0,880 |
|
0,12 |
0,703 |
0,180 |
1,28E+00 |
0,808 |
5,95E-01 |
0,917 |
|
0,14 |
0,765 |
0,210 |
9,34E-01 |
0,847 |
2,80E-01 |
0,934 |
|
0,16 |
0,825 |
0,240 |
6,80E-01 |
0,875 |
1,29E-01 |
0,943 |
|
0,18 |
0,828 |
0,270 |
4,95E-01 |
0,895 |
5,95E-02 |
0,947 |
|
0,20 |
0,850 |
0,300 |
3,61E-01 |
0,910 |
2,72E-02 |
0,948 |
|
0,22 |
0,900 |
0,330 |
2,63E-01 |
0,921 |
1,24E-02 |
0,949 |
|
0,24 |
0,900 |
0,360 |
1,91E-01 |
0,929 |
5,68E-03 |
0,950 |
|
0,26 |
0,925 |
0,390 |
1,39E-01 |
0,935 |
2,59E-03 |
0,950 |
|
0,28 |
0,925 |
0,420 |
1,01E-01 |
0,939 |
1,18E-03 |
0,950 |
|
0,30 |
0,925 |
0,450 |
7,39E-02 |
0,942 |
5,40E-04 |
0,950 |
|
0,32 |
0,950 |
0,480 |
5,38E-02 |
0,944 |
2,46E-04 |
0,950 |
|
0,34 |
0,925 |
0,510 |
3,92E-02 |
0,946 |
1,12E-04 |
0,950 |
|
0,36 |
0,925 |
0,540 |
2,85E-02 |
0,947 |
5,13E-05 |
0,950 |
|
0,38 |
0,925 |
0,570 |
2,08E-02 |
0,948 |
2,34E-05 |
0,950 |
|
0,4 |
0,925 |
0,600 |
1,51E-02 |
0,948 |
1,07E-05 |
0,950 |
|
0,42 |
|
0,630 |
1,10E-02 |
0,949 |
4,88E-06 |
0,950 |
Tracé
des différentes courbes.
Le modèle 1 est le mieux adapté pour décrire le mouvement de la bille dans l'huile.
C'est le modèle qui se rapproche le plus des valeurs expérimentales.
Dans l'huile, la force de frottement que subit la bille est de la forme :
- Modèle 1 :
f
= k1.v
- Équation différentielle :
- ![]()
![]() Calcul des constantes
α1 et
b.
Calcul des constantes
α1 et
b.
- ![]() et
et
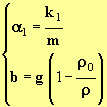
- La connaissance des différentes masses volumiques permet de calculer la valeur de b.
- 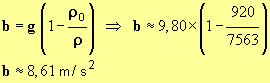
- à partir de la valeur de la vitesse limite, on peut calculer la valeur de α1.
- Lorsque le mobile a atteint sa vitesse limite,
- 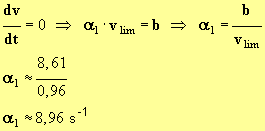
- Pour le modèle
1 : la
relation devient :
![]()
- Les conditions initiales sont les suivantes : au temps t0 = 0, v = v0.
- On choisit une valeur de δt suffisamment petite : C’est le pas du calcul.
- À la date t1 = t0 + δt, la vitesse est devenue : v1 = v0 + δv0 avec
- 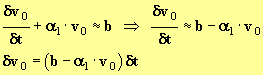
- en conséquence :
![]() ou
ou
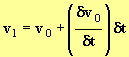
- Cette valeur est calculable puisque les valeurs α1, b et v0 sont connues.
- On procède de la même façon pour le calcul de v2.
- À la date
t2 =
t1 +
δt, la vitesse est devenue :
v2 =
v1 +
δv1
=
v1 + (b
- α1.v1).δt.
- À la date
tn+1 =
tn +
δt, la vitesse est devenue :
vn+1 =
vn +
δvn
=
vn + (b
- α1.vn).δt.
- On peut en répétant ce calcul, déterminer la valeur de la vitesse aux différentes dates séparées de δt.
- On peut ainsi obtenir la représentation graphique de v
en fonction du temps t.
- L’équation différentielle « a été résolue » numériquement par une méthode itérative.
Équation différentielle : Pour aller plus loin