I- Rappels.

1)- Le condensateur.

2)- La Bobine.

3)- Le conducteur ohmique.

II- Décharge d’un condensateur dans une bobine.

1)- Montage.

2)- Manipulation.

-  Première étape : on charge le condensateur en plaçant le commutateur sur la position 1.

-  Deuxième étape : on bascule le commutateur en position 2. On réalise ainsi un circuit (R, L, C) avec R = r + R’.

-  Quelles sont les tensions visualisées à la voie Y_A et à la voie Y_B ?

-  On visualise les variations de la tension u_AM en fonction du temps (tension aux bornes du condensateur) à la voie Y_A de l’oscilloscope.

-  On visualise les variations de la tension u_BM en fonction du temps (tension aux bornes du conducteur ohmique de résistance R’) à la voie Y_B de l’oscilloscope.

-  Quelle est la valeur prise par la tension u_AM lorsque le commutateur est en position 1 ?

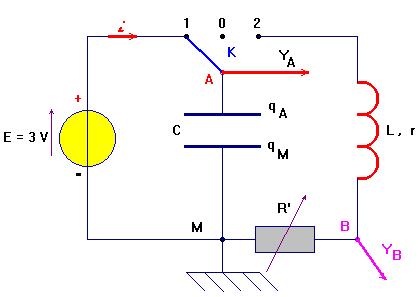
-  Lorsque le condensateur est chargé, u_AM = E = 3,0 V.

-  Qu’observe-t-on lorsque l’on bascule le commutateur sur la position 2 ?

3)- Observations.

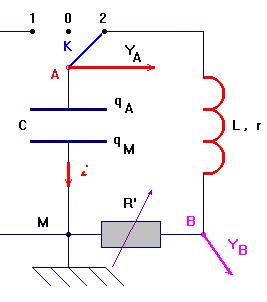
-  Lorsque le commutateur est en position 2, on constate que les tensions tension u_AM et u_BM prennent des valeurs alternativement positives et négatives.

-  On remarque aussi que leurs amplitudes diminuent au cours du temps.

-  La tension u_AM traduit les variations de la charge : q_A = C . u_AM

-  La tension u_BM traduit les variations de l’intensité dans le circuit  : 

-  Pour visualiser les variations de i dans le circuit, on appuie sur la touche  – B. 

-  Avec la carte candi-PCI, pour visualiser i, on tape l’expression : 

-  Le courant change alternativement de sens lors de la charge et de la décharge du condensateur.

-  L’amplitude des oscillations diminue au cours du temps car le circuit (R, L, C) perd progressivement,

-  l’énergie initialement emmagasinée dans le condensateur, par effet Joule dans les résistances.

-  En conséquence, un circuit électrique (R, L, C), réalisé avec un condensateur chargé, est le siège d’oscillations électriques libres amorties.

III- Influence de la résistance R du circuit sur les oscillations libres.

1)- Étude expérimentale.

a)- Avec la carte d’acquisition Candi-PCI :

Simulation avec Excel

-  Première étape : on charge le condensateur en plaçant le commutateur sur la position 1.

-  Deuxième étape : on bascule le commutateur en position 2.

-  On réalise ainsi un circuit (R, L, C) avec R = r + R’.

-  On renouvelle l’acquisition et entre chaque acquisition, on augmente la valeur de la résistance R’.

b)- Avec l’oscilloscope :

2)- Observations.

-  On observe des oscillations dont l’amplitude décroît au cours du temps.

-  Pour de faibles valeurs de la résistance R’, on observe des oscillations dont l’amplitude décroît progressivement : 

-  Le régime est pseudo-périodique.

-  Le phénomène possède une pseudo-période :

-  La pseudo-période T est la durée entre deux passages consécutifs par la valeur nulle de la tension, celle-ci variant dans le même sens.

-  On peut déterminer la valeur de la pseudo-période :

-  Selon la valeur de la résistance du circuit (R, L, C), on distingue les régimes : pseudo-périodique, critique, apériodique.

-  Il existe une valeur particulière R_C de la résistance R qui délimite les deux régimes. On l’appelle la résistance critique.

-  Si R < R_C , on observe des oscillations libres amorties, c’est le régime pseudo-périodique.

-  Si R = R_C , la tension tend rapidement vers zéro, c’est le régime critique.

-  Si R > R_C, la tension tend vers zéro sans oscillations, c’est le régime apériodique.

	R < RC , On observe des oscillations libres amorties, C’est le régime pseudo-périodique.
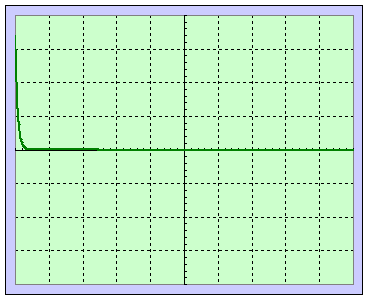	R = RC , la tension tend rapidement vers zéro, c’est le régime critique.
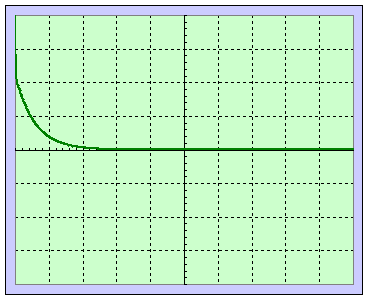	R > RC, La tension tend vers zéro sans oscillations, C’est le régime apériodique.

-  Lorsque l’amortissement est faible, la pseudo-période T est pratiquement égale à la période propre T₀ du circuit (L, C) sans résistance : 

-  T ≈ T₀.

IV- Influence de L et de C. (TP Physique N° 08)

1)- Montage :

2)- Influence de L.

-  On utilise dans un premier temps la bobine L₁ = 5 mH, puis L₂ = 20 mH. 

-  La valeur de la capacité de change pas, C = 1 μF.

-  On obtient les oscillogrammes suivants :

-  La valeur de la période est multipliée par deux lorsque celle de l’inductance est multipliée par quatre.

3)- Influence de C.

-  Dans un premier temps, on utilise un condensateur de capacité C₁ = 1 μF, puis C₂ = 4 μF. 

-  La valeur de l’inductance ne change pas L = 5 mH.

-  La valeur de la période est multipliée par deux lorsque celle de la capacité est multipliée par quatre.

4)- Conclusions :

-  La période propre d’un circuit (L, C) dépend de l’inductance de la bobine et de la capacité du condensateur

-  La période propre T₀ d’un dipôle (L, C) est la période des oscillations libres non amorties.

-  Elle est donnée par la relation :

-  Unités :  T₀ en seconde (s) , L en henry (H) et C en farad (F).

-  Dans un circuit peu amorti, la période propre est voisine de la pseudo période : T ≈ T₀

-  Analyse dimensionnelle.

-    

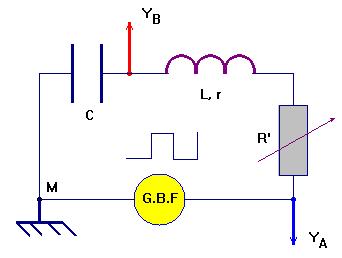
V- Étude analytique d’un circuit oscillant.

1)- Équation différentielle d’un circuit (R, L, C).

-  Montage :

-  On utilise l’additivité des tensions :

-  

-  On pose : R = R’ + r et on ordonne :

-  

-  Durant les oscillations libres amorties, la charge q du condensateur obéit à l’équation différentielle :

- 

2)- Équation différentielle d’un circuit (L, C).

-  Un circuit (L, C) est un circuit idéal de résistance nulle : R = 0.

-  En conséquence, la charge q du condensateur obéit à l’équation différentielle suivante :

- 

3)- Solutions de l’équation dans le cas d’un circuit (L, C).

-  L’équation différentielle  est une équation linéaire en q,  du second ordre, sans deuxième membre.

-  Elle admet une solution générale de la forme :

- 

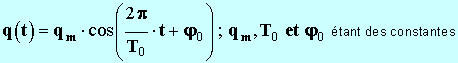
4)- Détermination des constantes.

-  On détermine les constantes à partir des paramètres du circuit et des conditions initiales.

-  Expression de :

-  

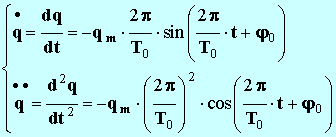
-  On remarque que :  

-  

-  En remplaçant dans l’équation différentielle :

-  

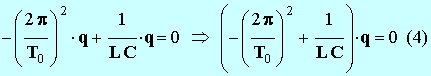
-  Cette équation est vérifiée ceci quel que soit t. Or 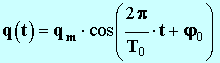 varie au cours du temps.

-  Il faut que

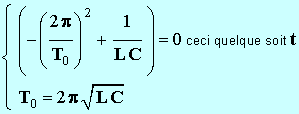
-  T₀ représente la période propre des oscillations.

-  Elle s’exprime en seconde s.

-  Conditions initiales :

-  à l’instant t = 0, l’intensité du courant dans le circuit est nulle

-  Or

- 

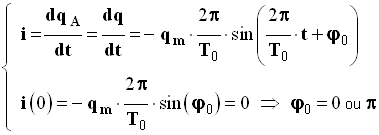
-  La grandeur φ₀ représente la phase à l’origine des dates.

-  Elle s’exprime en radian rad.

-  À l’instant initial, dans le cas qui nous intéresse, le condensateur est chargé,

-  il porte la charge q ₀ > 0, c’est la charge portée par l’armature A du condensateur au temps t = 0 s.

-  Au temps t = 0 s, soit :

-  Or, à l’instant initial, le condensateur porte la charge q ₀ > 0, comme la grandeur q _m est strictement positive, la solution est :

-  φ₀ = 0 et q (0) = q₀ = q _m  

-  On peut écrire :  

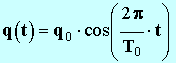
-  q₀ = q_m  représente l’amplitude de la charge. La charge du condensateur varie entre – q₀ et + q₀.

-  Elle s’exprime en coulomb C.

-  Remarque : on peut donner l’expression de la tension aux bornes du condensateur :

-  

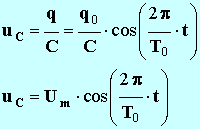
VI- énergie d’un circuit oscillant.

1)-   Transfert d’énergie en régime pseudo-périodique.

a)- Montage : Ordinateur et logiciel CONDO

fichier.zip

-  On observe les variations de la tension u_AM aux bornes du condensateur au cours du temps.

-  Grâce au logiciel, on peut visualiser les variations de l’énergie emmagasinée dans le condensateur et celle emmagasinée dans la bobine.

-  Avec :

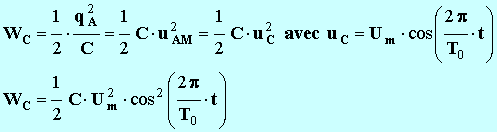
-  D’autre part : 

-    

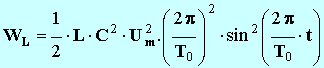
-  l’énergie du circuit (L, C) idéal :

-  

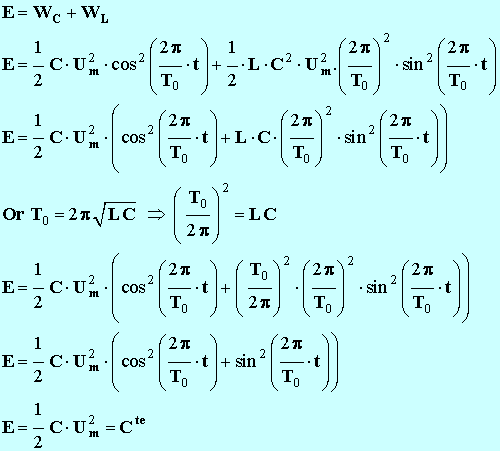
b)- Simulation à la calculatrice.

-  

-  Oscillogrammes :

Sans amortissement

Avec amortissement

2)- Conclusions.

-  Un circuit (L, C) possède deux réservoirs d’énergie entre lesquels des échanges d’énergie provoquent des oscillations électriques. 

-  Des échanges d’énergie se produisent entre le condensateur et la bobine.

-  Les variations de W_C et W_L sont périodiques, de période égale à la moitié de la période propre T₀ de l’oscillateur libre.

-  L’énergie du condensateur et l’énergie de la bobine varient en sens inverses.

-  Si l’amortissement est négligeable, l'énergie totale du système se conserve. 

-  Mais comme tout circuit électrique comporte une résistance R, l’énergie se dissipe par effet Joule.

-  Dans un circuit oscillant amorti, il y a échange d’énergie entre le condensateur et la bobine, mais l ‘énergie totale du circuit diminue progressivement par effet Joule.

3)- Entretien des oscillations.

-  Pour obtenir des oscillations non amorties dans un circuit (R, L, C), il faut lui fournir de l’énergie pour compenser les pertes par effet Joule dans les résistances. 

-  On introduit dans le circuit (R, L, C), un dipôle D dont le rôle est de fournir au circuit l’énergie perdue par effet Joule. 

-  Ce dipôle est appelé : ‘’montage à résistance négative’’.

-  Montage expérimental : utilisation de la carte Candi-PCI avec labo.

-  Manipulation :

-  Pour des valeurs faibles de R₀, on n’observe aucune oscillation. 

-  En augmentant la valeur de R₀, on parvient à une valeur particulière telle que les oscillations prennent naissance dans le circuit. 

-  Leur amplitude croît puis se stabilise.

-  Les oscillations paraissent sinusoïdales de période T₀ égale à la période propre du circuit (L, C).

-  Si  on augmente encore la valeur de R₀, les oscillations se déforment et ne paraissent plus sinusoïdales.

-  Avec ce dispositif, le circuit puise périodiquement, à sa propre fréquence l’énergie dans le dipôle D.

VII- Applications.

1)- QCM :

2)- EXERCICES :