Solution

1)- Branchements :

2)- Positions successives de l’interrupteur. 

-  Premier temps, on bascule l’interrupteur en position 1 : on charge le condensateur C. 

-  Deuxième temps, on bascule l’interrupteur en position 2 : on décharge le condensateur dans la bobine r, L. 

-  On visualise la décharge grâce à l’oscilloscope à mémoire.

3)- La bobine n’est pas idéale car l’amplitude des oscillations diminue au cours du temps. 

-  La bobine possède une résistance r faible mais non négligeable.

4)- On observe des oscillations libres amorties. Le régime est pseudo-périodique.

5)- Valeur de l’inductance L de la bobine

-  À l’aide de l’oscillogramme, on peut déterminer la valeur de la pseudo-période :

-  T₁ = b . x

-  T₁ = 1,0 x 4,0

-  T₁ ≈ 4,0 ms

-  Les oscillations étant peu amorties :

-  

6)- Si la valeur de la résistance R augmente et que R < R_C, le régime observé est pseudo-périodique

et l’amplitude des oscillations diminue de plus en plus rapidement.

-  Si R = R_C, on a atteint le régime critique.

-  Si R > R_C, on a atteint le régime apériodique. Il n’y a plus d’oscillations.

Solution

1)- Équation différentielle à laquelle obéit la tension u_C aux bornes du condensateur.

-  Schéma du circuit :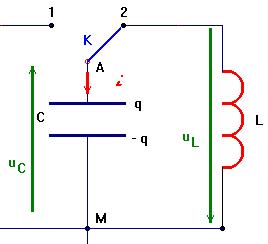

-  L’additivité des tensions :

-  

2)- expression de la tension :

-  Cette expression vérifie l’équation différentielle (1)

-  

-  En identifiant (1) et (1’) :

-  Au temps t = 0, le circuit est ouvert i (0) = 0 et u_C = 80 V.

-  

-  

-  période propre des oscillations et fréquence propre.

-  

3)- Influence de la résistance du circuit.

a)- Schéma du circuit.

  b)- Le régime des oscillations.

-  Courbe a : R₂ = 100 Ω : Régime pseudo-périodique. Le système effectue des oscillations libres amorties.

-  Courbe b : R₃ = 400 Ω : Régime pseudo-périodique. Le système effectue des oscillations libres  très amorties.

-  Courbe c : R₁ = 2200 Ω  Régime apériodique. Le système n’effectue pas d’oscillation.

On considère un circuit LC idéal. En plaçant un interrupteur K sur la position 1,

on charge le condensateur sous la tension E = 10 V. 

à l’instant t = 0, on bascule l’interrupteur sur la position 2.

Il s’établit un courant sinusoïdal i, pour lequel l’orientation est indiquée.

La charge du condensateur évolue au cours du temps selon :

q (t) = q_m cos (α . t + k).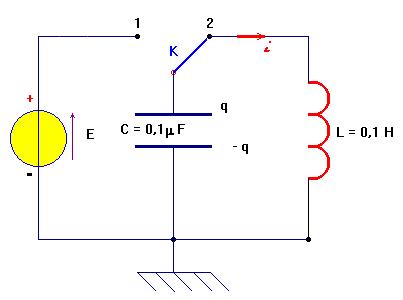

1)- À l’instant t = 0,

la charge du condensateur vaut :

    q₀ =  10 ^– 6  C

VRAI : q₀ = C . E ≈  10 ^{– 6}  C

2)- L’intensité du courant i a

pour expression :

FAUX : avec l’orientation choisie :

3)- La période des oscillations est : 

T ≈ 0,6 s

FAUX : 

4)- L’intensité en ampère est :

FAUX :

On donne :  q (t) = q _m cos (α. t + k)

Or  

Les conditions initiales donnent :

t = 0 , i (0) = 0

 i (t) = - a . q _m sin (a t + k) 

Au temps t = 0,

le condensateur est chargé

et il porte la charge

q (0) = C E = q₀ qui est positive.

En conséquence : q_m = q₀ et k = 0.

Un condensateur de capacité C = 0,25 μF est chargé à l’aide d’un générateur de tension de f.é.m. E = 6,0 V,

puis déconnecté du générateur.

À la date t = 0, le condensateur chargé est relié à une bobine d’inductance L et de résistance r.

L’évolution au cours du temps de la tension u_C aux bornes du condensateur est enregistrée à l’aide d’un ordinateur

(le condensateur est étudié en convention récepteur).

1)- Comment appelle-t-on le type d’oscillations observées ?

-  On est en présence d’oscillations libres amorties. Le régime observé est pseudo-périodique.

2)- Comment interpréter la décroissance des oscillations ?

-  Du fait de la présence d’une résistance dans le circuit,

-  le système dissipe de l’énergie par effet Joule au cours des oscillations.

3)- Établir l’équation différentielle à laquelle satisfait u_C.

-  

4)- Mesurer la pseudo-période T’ des oscillations.

-  T’ ≈ 1,0 ms.

5)- On considère que la résistance r de la bobine est nulle.

a)- Écrire la nouvelle équation différentielle satisfaite par u _C.

-  Équation différentielle satisfaite par u _C

- 

b)- La solution de l’équation s’écrit : u_C (t) = U cos( α . t + φ). Déterminer les expressions des constantes  U,  α  et φ.

-  Cette solution vérifie l’équation différentielle (2) :

-  

-  En identifiant :

- 

-  Or :

- 

-  Au temps t = 0, le condensateur est chargé et

-  la tension aux bornes du condensateur vaut 6,0 V.

-  D’autre part, l’intensité i (0) = 0.

-  

-  D’autre part : 

-  u_C (t) = U cos( α t + φ)

-  u_C (0) = U cos( α x 0 + φ) = 6,0 V > 0

-  φ = 0  et U = E = 6,0 V

-  

c)- en déduire l’expression de la charge q (t) du condensateur et de l’intensité i (t) à l’instant t.

-  Expression de la charge q :

- 

-  Expression de l’intensité i :

- 

d)- Quelle est l’expression littérale de la période des oscillations qui prennent naissance dans le circuit ?

-  Période des oscillations du circuit L C.

-  

6)- Calculer  la valeur de l’inductance L de la bobine en admettant que la pseudo-période est identique à la période.

-  Inductance de la bobine :

- 

On réalise le circuit schématisé ci-dessous.

Le condensateur de capacité C = 15 μF est préalablement chargé à l’aide d’un générateur idéal de tension continue

(interrupteur en position 1).

Il se décharge ensuite à travers un circuit comportant une bobine d’inductance L = 1,0 H et de résistance r

(Interrupteur en position2).

I- Étude du circuit.

1)- Un dispositif d’acquisition relié à un ordinateur permet de suivre pendant la décharge,

d’une part l’évolution au cours du temps de la tension par u_C aux bornes du condensateur,

et d’autre part celle de l’intensité i du courant.

a)- Les oscillations sont-elles libres ou entretenues ? Sans calcul, justifier la réponse.

-  On est en présence d’oscillations libres amorties. 

-  Le circuit ne comporte pas de générateur permettant de compenser les pertes d’énergie dans le circuit par effet Joule. 

-  Le système possède deux réservoirs d’énergie le condensateur et la bobine.

b)- Déterminer à partir des courbes la valeur de la pseudo-période T des oscillations.

-  Pseudo-période :

-  Graphiquement, T ≈ 24 ms

c)- Établir la relation entre l’intensité i du courant et la tension par u_C aux bornes du condensateur

en respectant les conventions indiquées sur le schéma.

-  Relations :

d)- Entre les instants t_A et t_B, le condensateur se charge-t-il ? Où se décharge-t-il ? Justifier la réponse.

-  À l’instant t_A , le condensateur est chargé et l’intensité dans le circuit est nulle. 

-  Puis le condensateur se décharge, la tension u_C est positive et elle diminue pour s’annuler à l’instant t _B. 

-  Le condensateur se décharge.

e)- À partir de la courbe traduisant u_C (t), et en utilisant la relation de la question 1)- c)-,

retrouver la valeur de i à l’instant t_A et le sens réel de circulation du courant entre t_A et t_B.

-  À l’instant t_A , la tension est maximale.

-  Comme :  , l’intensité du courant qui traverse le circuit est nulle. 

-  Entre t_A et t_B, l’intensité est négative.

-  Le courant circule dans le sens inverse du sens positif choisi.

2)- On souhaite étudier l’énergie totale E de l’oscillateur électrique.

Cette énergie est la somme de l’énergie E_cond stockée dans le condensateur et de l’énergie E_bob emmagasinée dans la bobine.

Le logiciel utilisé peut calculer, à partir des mesures,

les valeurs de ces trois énergies et fournir les courbes donnant leurs variations au cours du temps.

a)- Rappeler l’expression de : l’énergie E_cond ; de l’énergie E_bob.

-  

b)- L’origine des dates étant la même pour toutes les mesures,

identifier les trois courbes ci-dessus en ne  justifiant que l’identification de la courbe donnant les variations de E_bob au cours du temps.

-  La courbe 1 représente les variations de l ‘énergie stockée dans le condensateur E_cond .

-  Au départ, le condensateur est chargé et l’intensité dans le circuit est nulle.

-  La courbe 2 représente les variations de l’énergie emmagasinée dans la bobine E_bob au cours du temps.

-  Il y a échange mutuelle d’énergie entre la bobine et le condensateur.

-  Lorsque l’énergie stockée dans le condensateur est maximale, l’énergie emmagasinée dans la bobine est nulle et inversement.

-  La courbe 3 représente les variations de l’énergie totale E.

c)- Interpréter brièvement la décroissance de l’énergie totale de l’oscillateur électrique.

-  Le circuit comportant une résistance, au cours des oscillations, l’énergie initiale est dissipée par effet Joule. 

-  Il en résulte que l’énergie du système diminue au cours du temps.

II- Modélisation.

On suppose maintenant que l’oscillateur ne comporte aucune résistance.

Dans ces conditions, la tension u_C aux bornes du condensateur est de la forme : .

1)- Établir l’équation différentielle vérifiée par u_C (t) et préciser les conditions aux limites.

-  Équation différentielle :

-  Au temps t = 0, le condensateur est chargé et la tension aux bornes du condensateur vaut E.

-  D’autre part, l’intensité i (0) = 0.

2)- Calculer la période T₀ et la comparer à la pseudo-période T déterminée au I- 1)- b)-.

-  Période propre des oscillations :  

-  

3)- Que peut-on dire des oscillations ? Comment qualifie-t-on le régime d’oscillations ?

-  On est en présence d’oscillations libres non amorties.

-  Il faut adjoindre au circuit un dipôle D qui compensent les pertes par effet Joule.

-  Ce dispositif apporte l’énergie nécessaire à l’entretient des oscillations et au rythme propre du circuit.

4)-  

a)- établir, en fonction des grandeurs C, U_m, T₀  et t  les expressions de :

-  L’intensité du courant i(t) traversant le circuit électrique ;

-  Sachant que :

-  

-  L’énergie E_cond stockée dans le condensateur ;

-  

-  L‘énergie E _bob emmagasinée dans la bobine.

-  

b)-     Montrer que, dans ce cas, l’énergie totale de l’oscillateur est conservée.

-  Énergie totale :

-  

-