|
|
|
|
|
|
|
|
Exercices : DS
|
|
QCM r
|
1)- Exercice 06 : Circuit (L, C) et énergie :
|
Circuit (L, C) et énergie : Le condensateur d’un circuit oscillant non amorti a une capacité
C = 2,2 µF. Il est initialement chargé sous une tension de 12 V. 1.
Calculer l’énergie initiale du circuit
oscillant. 2.
Calculer la valeur maximale de l’énergie
emmagasinée par la bobine lors des oscillations. 3.
Calculer la valeur maximale de l’intensité
du courant dans le circuit si L = 0,10 H. |
|
Circuit (L, C) et énergie 1.
Énergie initiale du circuit oscillant.
-
Schéma du condensateur chargé :
-
Énergie emmagasinée par le
condensateur chargé :
-
Un condensateur de capacité
C, chargé sous une tension uC,
emmagasine de l’énergie :
-
C’est de l’énergie potentielle
électrostatique.
-
2.
Valeur maximale de l’énergie emmagasinée par
la bobine lors des oscillations.
-
Bobine d’inductance L :
-
Courant d’intensité i :
-
Une bobine d'inductance
L, traversée par
un courant d’intensité i, emmagasine de l'énergie.
-
C'est de l'énergie magnétique que
l'on note
-
L’intensité du courant électrique
dans un circuit comportant une bobine ne subit pas de discontinuité.
-
Le courant s’établit de façon
progressive et s’annule de la même façon.
-
L’intensité du courant électrique ne
peut pas passer de façon instantanée de la valeur zéro à la valeur
I.
-
Schéma du circuit :
-
Le circuit ne comporte pas de
résistance r.
-
L’énergie totale du système se
conserve car il est non amorti.
-
Il y a échange mutuel d’énergie entre
le condensateur et la bobine.
-
E =
WC +
WL = cte
-
E =
WC +
WL ≈ 1,6 × 10–4 J - L’énergie emmagasinée par la bobine est maximale lorsque l’énergie emmagasinée par le condensateur est
nulle (le condensateur est alors
déchargé).
-
WL ≈ 1,6 × 10–4
J 3.
Valeur maximale de l’intensité du courant
dans le circuit si L = 0,10 H.
-
|
||||||||||||||||
2)- Exercice 07 : Étude d’un oscillogramme d’un circuit (L, C) :
|
Étude d’un oscillogramme d’un circuit (L, C) : La figure représente l’oscillogramme de la tension aux bornes
d’un condensateur d’un circuit (L, C). Données :
-
C = 6,9 µF ;
-
Sensibilité verticale :
k = 2 V . div–1 ;
-
Durée de balayage (sensibilité
horizontale) : b = 1 ms
. div–1.
1.
Déterminer la période des oscillations. 2.
Quelle est la valeur de l’inductance L ? 3.
Calculer l’énergie que possède le circuit
oscillant. 4.
Calculer la valeur maximale de l’intensité
du courant dans le circuit. |
|
Étude d’un oscillogramme d’un circuit (L, C) :
-
Montage :
-
Oscillogramme :
1.
Période des oscillations.
-
Oscillogramme :
-
T =
x .
b
-
T ≈ 4,0 × 1,0
-
T ≈ 4,0 ms 2.
Valeur de l’inductance L.
-
-
Application numérique :
-
3.
Énergie que possède le circuit oscillant.
-
Le circuit ne comporte pas de
résistance r.
-
L’énergie totale du système se
conserve car il est non amorti.
-
Il y a échange mutuel d’énergie entre
le condensateur et la bobine.
-
E =
WC +
WL = cte - L’oscillogramme obtenu représente les variations de la tension aux bornes d
u condensateur aux cours du
temps. - Lorsque la tension est maximale, l’énergie aux bornes du condensateur est maximale
et l’énergie aux
bornes de la bobine est nulle. - Lorsque la tension est nulle, l’énergie aux bornes de la bobine est maximale
et celle aux bornes du condensateur est nulle.
-
Tension aux bornes du condensateur
lorsqu’il est chargé :
-
U0 =
y .
k
-
U0 ≈ 3,0 × 2,0
-
U0 ≈ 6,0 V
-
Énergie emmagasinée par le
condensateur chargé
-
4.
Valeur maximale de l’intensité du courant
dans le circuit.
-
|
3)- Exercice 09 : Oscillations électriques amorties :
|
Oscillations électriques amorties : Les courbes suivantes représentent les oscillations électriques (tension aux bornes du condensateur) de deux circuits oscillants (R, L, C) ayant
la même inductance L.
1. Lequel des deux circuits, (a) ou (b), possède-t-il la plus grande résistance ? Justifier la réponse. 2.
Ces deux circuits ont-ils la même capacité ?
Justifier la réponse. |
Oscillations électriques amorties :
-
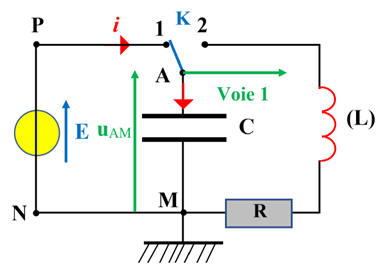
Schéma :
-
On charge le condensateur en mettant
l’interrupteur sur la position 1.
-
Puis, on bascule l’interrupteur on
position 2 et on observe les oscillations à la voie 1 de
l’oscilloscope à mémoire. 1.
Comparaison des résistances des deux
circuits.
-
L’amortissement est plus important
pour le circuit (b) que
pour le circuit (a).
-
L’amplitude des oscillations diminue
plus rapidement pour le circuit (b)
que pour le circuit (a).
-
Le circuit (b)
possède la plus grande résistance
R car il est plus amorti
que le circuit (a).
-
L’amortissement augmente avec la
valeur de la résistance R
du circuit.
-
L’énergie est dissipée par effet
Joule dans la résistance du circuit.
-
Mais comme tout circuit électrique
comporte une résistance R, l’énergie se dissipe par effet
Joule.
-
Dans un circuit oscillant amorti, il
y a échange d’énergie entre le condensateur et la bobine, mais
l’énergie totale du circuit diminue progressivement par effet Joule.
-
Elle diminue d’autant plus rapidement
que la valeur de la résistance
R du circuit est grande. 2.
Comparaison des capacités des deux circuits.
-
Comme l’amortissement est faible dans
les deux cas, on peut considérer que la pseudo-période est voisine
de la période propre du circuit.
-
-
Les deux signaux ont sensiblement la
même période T.
![]()
![]()
4)- Exercice 10 : Circuit (R, L, C) alimenté en créneaux :
|
Circuit (R, L, C) alimenté en créneaux :
Un circuit (R, L, C) est alimenté par un
générateur de signaux rectangulaires. La bobine a une inductance L = 4,7 mH et le condensateur
une capacité C = 1,0 µF. 1.
Faire le schéma du montage. 2.
Calculer la période propre des oscillations. 3. La visualisation de la tension aux bornes du condensateur montre que l’amplitude est quasiment nulle après dix oscillations. Sur quelle fréquence convient-il de régler le générateur de signaux pour visualiser le phénomène dans les meilleures conditions. En déduire une valeur de la base
de temps b de l’oscilloscope. |
Un circuit (R, L, C) est alimenté par un
générateur de signaux rectangulaires.
-
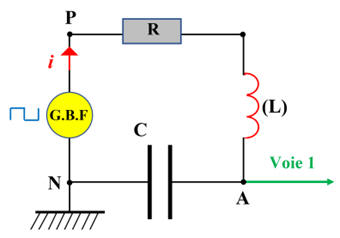
1.
Schéma du montage. 2.
Période propre des oscillations.
-
3.
Valeur de la base de temps b de
l’oscilloscope.
-
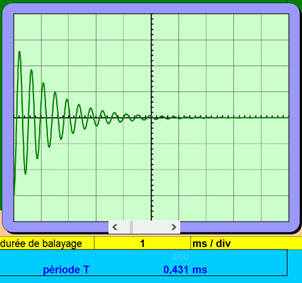
Visualisation du phénomène à
l’oscilloscope :
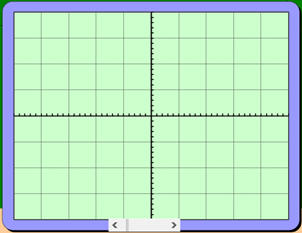
-
L’écran de l’oscilloscope :
-
Si l’on veut montrer 10
oscillations :
-
Δt ≈ 4,3 ms :
-
Pour
b = 1 ms . div–1
-
Visualisation :
-
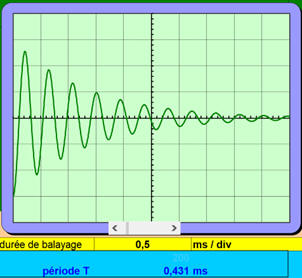
Pour
b = 0,5 ms . div–1
-
Visualisation :
-
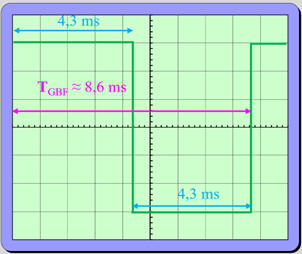
Fréquence du
G.B.F :
-
TGBF ≈ 8,6 ms
-
Fréquence du
G.B.F :
-
-
Pour la fréquence du
G.B.F, on peut choisir 100 Hz.
-
Oscillogramme :
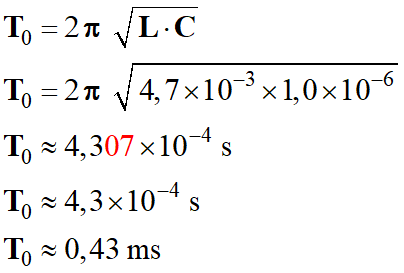
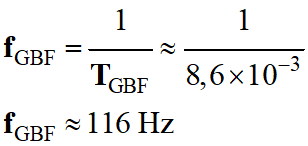
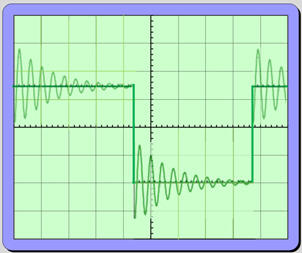
![]()
5)- Exercice 21 : Exploitation de documents :
|
Exploitation de documents : Les documents précédents sont des enregistrements de la tension
aux bornes d’un condensateur de deux circuits (R, L,
C) différents. 1.
Évaluer la ,pseudo-période des oscillations
enregistrées sur le document (a). 2. Le circuit correspondant à l’enregistrement (a) comportait une bobine d’inductance L = 0,50 H et de résistance r = 10 Ω, et un condensateur de capacité C = 4,0 µF. Comparer la valeur expérimentale
à la valeur théorique en supposant que l’amortissement est
négligeable. 3. L’enregistrement (b) est réalisé avec la même bobine, mais avec un autre condensateur. Déterminer la capacité de
celui-ci par comparaison des périodes. 4. Dans quel cas l’amortissement est-il le plus important ? Indiquer les paramètres qui
influent sur l’amortissement des oscillations. Conclure. |
|
Exploitation de documents : 1.
Pseudo-période des oscillations enregistrées
sur le document (a).
-
Exploitation de l’oscillogramme :
-
On travaille sur 10 périodes pour
plus de précision :
-
Ta ≈ 8,9 ms
2.
Comparaison la valeur expérimentale à la
valeur théorique.
-
Enregistrement (a) :
-
Bobine d’inductance
L = 0,50 H
-
Résistance
r = 10 Ω,
-
Condensateur de capacité
C = 4,0 µF
-
L’amortissement est négligeable :
-
La période propre T0
d’un dipôle (L, C) est la période des oscillations libres non
amorties.
-
Elle est donnée par la relation :
-
-
Unités :
T0
en seconde (s) , L en
Henry (H) et C en Farad
(F).
-
Dans un circuit peu amorti, la
période propre est voisine de la pseudo période :
-
T0 ≈ T.
-
Application numérique :
-
-
En conséquence :
-
T0 ≈ Ta
-
La pseudo-période est sensiblement
égale à la période propre du circuit.
-
On est bien dans le cas où
l’amortissement est négligeable.
-
Valeur de la pseudo-période T
:
-
-
Application numérique :
-
►
Additif : 3. Déterminer la capacité C du
condensateur par comparaison des périodes.
-
L’enregistrement (b) est réalisé avec la même bobine, mais avec un autre condensateur.
-
Exploitation de l’oscillogramme :
-
On travaille sur 20 périodes pour
plus de précision :
-
Tb ≈ 8,9 ms
-
Comme l’amortissement est faible :
-
T0b ≈ Tb
-
-
Remarque : T0b ≈ 2
T0a
-
Ca = 4
Cb 4.
Paramètres qui influent sur l’amortissement
des oscillations.
-
Dans le cas du circuit (b), l’amortissement est plus important car l’amplitude diminue plus
rapidement.
-
L’amortissement des oscillations
dépend de la résistance totale du circuit
RT.
-
Si
RT = 0 Ω, on
observe des oscillations libres non amorties (cas idéal).
-
Si 0 <
RT >
RC, on observe
des oscillations libres amorties (régime pseudopériodique).
-
Si
RT =
RC, on
n’observe pas d’oscillation (régime critique).
-
Si RT >
RC, on
n’observe pas d’oscillation (régime apériodique).
-
On utilise
l’additivité des tensions :
-
-
On pose :
R
=
R’
+
r
et on ordonne :
-
-
Durant les
oscillations libres amorties, la charge
q
du condensateur obéit à l’équation différentielle :
-
-
Formulation générale :
-
-
On pose :
-
-
Le termeλest lié à
l’amortissement du système.
-
Le terme ω02
est lié à la pulsation propre du système :
-
On obtient l’équation
générale suivante :
-
-
On retrouve cette
forme d’équation différentielle aussi bien en mécanique qu’en électricité.
|
|
|