I- Mise en évidence du phénomène d'auto-induction.

1)- Expériences.

- Montage 1 :

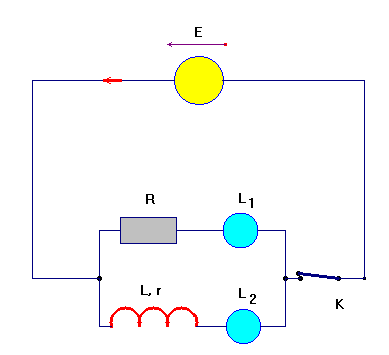
- Observations : La lampe L₂ s'allume avec un retard sur la lampe L₁.

Il se produit un retard à l'établissement du courant dans la portion de circuit qui comporte la bobine.

 - Montage 2 : visualisation du phénomène à l'oscilloscope.

- Il comprend :

- Un G.B.F qui délivre une tension carrée.

- Un conducteur ohmique de résistance R₁ réglable de 0 à 500 Ω.

- Une bobine d'inductance L = 20 mH et de résistance r = 20 Ω.

- Un conducteur ohmique de résistance R = 18 Ω.

- Que visualise-t-on à la voie A de l'oscilloscope ?

- On visualise les variations de la tension aux bornes du G.B.F, c'est-à-dire la tension u_AM.

- Que visualise-t-on à la voie B de l'oscilloscope ?

- On visualise les variations de la tension aux bornes du conducteur ohmique de résistance R₁, c'est-à-dire la tension u_BM.

- Si l'on considère qu'au temps t, le courant circule dans le sens positif choisi,

- .

- On visualise les variations de l'intensité en fonction du temps, ceci à une constante près.

- Observations :

- La courbe qui apparaît à la voie B, ne suit pas exactement les variations de celle qui apparaît à la voie A.

- Il y a un retard à l'établissement et à l'annulation du courant dans le circuit.

2)- Interprétation.

• Premier temps :

- t € [ t₀, t₀ + Δt] : régime transitoire, établissement du courant dans la bobine.

- t € [t₀ + Δt, t₁]: régime permanent, le courant est établi.

- La bobine s'oppose à l'établissement du courant dans le circuit.

• Deuxième temps :

- : régime transitoire, annulation du courant dans la bobine.

- : régime permanent, le courant est nul.

- La bobine s'oppose à l'annulation du courant dans le circuit.

  Lorsque l'on ferme ou ouvre le circuit, on fait varier l'intensité i du courant dans la bobine.

- Cette variation de i produit une variation du champ magnétique créé par la bobine.

- Cette variation du champ magnétique propre de la bobine entraîne l'apparition d'une f.é.m d'induction dans la bobine.

- La bobine crée un courant induit qui engendre un champ magnétique induit qui s'oppose au champ magnétique propre qu'elle produit.

- Ce phénomène est appelé : phénomène d'auto-induction (la bobine agit sur elle-même)

- C'est un phénomène transitoire.

II- F.é.m d'auto-induction.

1)- Expression de la f.é.m : e.

a)- Établissement du courant :

- Au cours de l'établissement du courant, la valeur de l'intensité augmente :

- i ↑  =>  di > 0

- Pour s'opposer à cette croissance, tout se passe comme si la bobine se comportait comme un générateur ,

monté en opposition, de f.é.m négative, donnant un courant induit i' de sens opposé au courant i.

- La bobine se comporte comme un récepteur de f.c.é.m : e < 0.

b)- Annulation du courant :

- Au cours de l'annulation du courant, la valeur de l'intensité diminue :

-  i ↓  =>  di < 0

- Pour s'opposer à cette décroissance, la bobine se comporte comme un générateur de f.é.m positive donnant un courant induit i'de même sens que le courant i.

c)- Conclusion :

En régime variable, le courant ne s'établit pas instantanément. La bobine se comporte comme un électromoteur ceci tant que i varie.

d)- La Loi de LENZ - FARADAY.

L'inductance propre L de la bobine est une constante positive qui ne dépend que des caractéristiques géométriques de la bobine Pour un solénoïde de longueur ℓ, qui possède N spires de surface S

  2)- Loi d'Ohm aux bornes d'une bobine. Schéma équivalent.

 

- Une bobine est caractérisée par son inductance L et sa résistance r. - Tant que i varie, la bobine se comporte comme un électromoteur, elle est donc équivalente à l'association série d'une générateur de tension de f.é.m : e (grandeur algébrique) et d'un conducteur ohmique de résistance r.   - Ceci aux bornes d'une bobine (L, r) de bornes A et B, orientée de A vers B.

3)- Application : exercice 7 page 251.

- L'intensité du courant dans une bobine d'inductance L = 0,10 H varie en fonction du temps selon la loi indiquée par le graphique ci-dessous. - Écrire l'expression de la f.é.m d'auto-induction e. - Calculer la f.é.m : e dans différents intervalles de temps. - Représenter graphiquement la variation de e au cours du temps.

 

- Expression de la f.é.m : - - F.é.m dans l'intervalle de temps -   - - Représentation graphique :

 - Réponses :

III- Étude du régime transitoire. (TP Physique N° 12).

 1)- Montage.

 2)- Constante de temps du circuit (R, L).

- La constante de temps τ du circuit (R, L) est donnée par la relation :

-

- Analyse dimensionnelle :

-

- Le rapport a bien la dimension d'un temps.

 3)- Intensité du courant et tension aux bornes de la bobine.

- Tension aux bornes de la bobine :

- Tension aux bornes du conducteur ohmique :

- Tension aux bornes du générateur :

- En régime permanent :

- Au temps t = 0 s :

- représente le coefficient directeur de la tangente à l'origine à la courbe i = h (t).

- L'abscisse du point d'intersection de l'asymptote horizontale I₀ et de la tangente à l'origine donne la constante de temps τ du circuit (R, L).

- L'augmentation de l'intensité i du courant est d'autant plus rapide que la constante de temps t est petite.

4)- Application : exercice 13 page 252.

IV- Énergie emmagasinée dans une bobine.

1)- Expérience : Étincelle de rupture

a)- Montage :

L = 0,1 H et r = 4 Ω

b)- Observations :

- Les étincelles de rupture montrent que l'énergie emmagasinée dans la bobine est libérée brutalement lors de l'ouverture du circuit.

- L'étincelle correspond à la conduction de l'air.

- Si le stylet est distant de 0,1 mm, alors , |e| ≈ 300 V  , E ≈ 300 000 V / m, potentiel disruptif de l'air sec.

2)- Expression de l'énergie emmagasinée dans une bobine.

- Une bobine d'inductance L emmagasine de l'énergie.

C'est de l'énergie magnétique que l'on note E_m ou W_L.

V- Applications : exercices : 7, 9, 13, 15, 16 ,19 pages 252-254.