![]()
|
|
|
|
|
|
|
|
QCM r
|
1)- Exercice 07 : Intensité du courant dans une bobine :
|
Intensité du courant dans une bobine : L’intensité du courant dans une bobine d’inductance L = 0,10 H varie en fonction du temps selon la loi indiquée par le graphique ci-dessous.
1.
Écrire l’expression de la f.é.m. e
d’auto-induction. 2.
Calculer la f.é.m. e d’auto-induction
dans les différents intervalles de temps. 3.
Représenter graphiquement la variation de
e au cours du temps. |
|
Intensité du courant dans une bobine : Oscillogramme :
-
- L'inductance propre L de la bobine est une constante positive qui ne dépend que des caractéristiques
géométriques de la bobine.
-
Exemple :
-
Pour un solénoïde de longueur
ℓ, qui possède
N spires de
surface :
-
►
Loi d'Ohm aux bornes d'une bobine.
Schéma équivalent.
-
Une bobine est caractérisée par son
inductance L
et sa résistance r. - Tant que i varie, la bobine se comporte comme un électromoteur, elle est donc équivalente à l'association série d'un générateur de tension de f.é.m. e (grandeur algébrique) et d'un conducteur ohmique de
résistance r.
-
-
Ceci aux bornes d'une bobine
(L, r) de bornes
A et
B, orientée de
A vers
B. 2.
Valeur de la f.é.m. e
d’auto-induction dans les différents intervalles de temps.
-
1ier cas : t € [0,0
ms ; 3,0 ms]
-
La grandeur
i (t) est du type i (t) = a
. t
-
La grandeur a est le
coefficient directeur du segment de droite
AB.
-
-
Or :
-
-
2ième cas :
t € [3,0 ms ; 5,0 ms]
-
La grandeur i (t) est du type
i (t) = a’ . t + b’
-
La grandeur a’ est le
coefficient directeur du segment de droite
BC.
-
-
Or :
-
3.
Représentation graphiquement de la variation
de e au cours du temps.
-
Oscillogramme :
|
||||||||
2)- Exercice 09 : Inductance d’une bobine sans fer :
|
Inductance d’une bobine sans fer L’inductance d’un solénoïde long est donnée par l’expression
approchée :
Avec : N : le nombre de spires ; ℓ : longueur du solénoïde en mètre (m) ; S : La surface d’uns spire ; μ0 = 4 π
× 10–
7 S.I (Henry / mètre : H / m). 1.
Un solénoïde de 50 cm de longueur, de 6,0 cm
de diamètre, comporte 1000 spires. Calculer son inductance L. 2.
Quelle est la f.é.m. d’auto-induction qui
apparaît dans la bobine, lorsque l’intensité du courant qui la
traverse a un taux de variation de 200 A . s–1 ? 3. On introduit dans la bobine un noyau de fer doux. Le taux de variation de i est le même. La valeur de la f.é.m.
d’induction augmente-t-elle ou diminue-t-elle ? |
|
Inductance d’une bobine sans fer L’inductance d’un solénoïde long est donnée par l’expression
approchée :
-
1.
Valeur de l’inductance L du
solénoïde.
-
Longueur du solénoïde : ℓ = 50
cm
-
Diamètre du solénoïde : D =
6,0 cm
-
Surface d’une spire :
-
Nombre de spires : N = 1000
spires.
-
-
Application numérique :
-
2.
F.é.m. d’auto-induction aux bornes de la
bobine :
-
L’intensité du courant qui traverse
la bobine a un taux de variation de 200 A . s–1
-
On donne le taux de variation :
-
-
3.
Influence du noyau de fer doux sur la valeur
de la f.é.m. d’induction :
-
Si on introduit un noyau de fer doux,
la valeur de l’inductance L du solénoïde augmente.
-
En conséquence, la valeur de la
f.é.m. aux bornes du solénoïde augmente. |
3)- Exercice 13 : Constante de temps :
|
Constante de temps : Dans un circuit (L, R), on a relevé la valeur de
l’intensité i du courant en fonction du temps : Graphe : 1.
Quelle est la valeur de l’intensité du
courant en régime permanent. 2.
On désire déterminer, à partir du graphique,
la constante de temps τ par trois méthodes : a. Tracer la tangente à la courbe à l’instant t = 0. À partir du point d’intersection
avec l’asymptote horizontale de la courbe, déduire la valeur de τ. b. Au bout d’une durée τ après l’établissement du courant, l’intensité est égale à 63 % de sa valeur maximale. À l’aide du graphique en déduire
la valeur de τ. c. L’intensité passe d’une valeur égale à 10 % de sa valeur maximale à une valeur égale à 90 % de sa valeur maximale sur une durée Δt = 2,2 τ. À l’aide du graphique, en
déduire la valeur de τ. d.
Comparer les valeurs de τ. 3.
Calculer la valeur de l’inductance de la
bobine si R = 11 Ω. 4.
Calculer la valeur
5.
En déduire la valeur de la f.é.m. aux bornes
de la bobine au temps t = 0. |
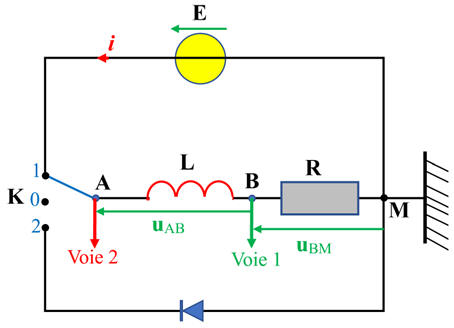
Constante de temps :
-
Graphe :
-
Montage :
-
Établissement du courant dans la
bobine :
-
On ferme l’interrupteur. On oriente
le circuit et on étudie le dipôle (R, L).
-
La loi d’additivité des tensions dans
le circuit série permet d’écrire :
-
-
En ordonnant, on peut écrire :
-
-
On reconnaît une équation
différentielle du premier ordre avec deuxième membre qui admet une
solution du type :
-
►
Détermination des constantes.
-
On détermine les constantes à l’aide
des conditions initiales et des paramètres du circuit.
-
Première étape :
-
On reporte l’expression de la
solution dans l’équation (1).
-
-
La relation (2) est vérifiée à chaque
instant.
-
Or E = cte et R
. B = cte et
-
t et par conséquence ek
. t varient au cours du temps.
-
Il faut nécessairement que :
-
-
La solution A = 0 n’a pas de
signification physique.
-
En conséquence :
-
-
conditions
initiales : au temps
t = 0 s,
-
L’intensité dans le circuit est
nulle : i (0) = 0.
-
On déduit de ceci que :
-
-
Relation donnant l’intensité
traversant le dipôle (R, L) soumis à un échelon de
tension E :
-
-
Grandeur caractéristique du circuit (R,
L) :
-
La constante de temps τ est
une grandeur caractéristique du circuit (R, L).
-
On appelle constante de temps du
circuit (R, L), la valeur
-
Lors de l’établissement du courant,
l’expression de l’intensité du courant électrique dans le circuit
est donnée par l’expression :
-
1.
Valeur de l’intensité du courant en régime
permanent.
-
L’intensité traversant le circuit est
nulle juste après la fermeture de l’interrupteur
K, puis elle
augmente progressivement jusqu’à atteindre une valeur maximale et
reste constante.
-
Le courant met environ la durée
Δt
≈ 40 ms pour s’établir.
-
La courbe présent un régime
transitoire ( t € [0 ;
Δt]
) et un régime permanent ( t € [Δt ;
t1) ]
-
Valeur de l’intensité du courant
permanent :
-
i0 ≈ 0,055 A = 55
mA. 2.
Détermination, à partir du graphique, la
constante de temps τ par trois méthodes : a.
Méthode de la tangente à la courbe à
l’instant t = 0.
-
Pour déterminer graphiquement la
valeur de τ, on trace la tangente à l’origine à la courbe
i = g (t) et l’asymptote horizontale à cette
courbe.
-
L’abscisse du point d’intersection de
ces deux droites donne la valeur de la constante de temps τ.
-
Exploitation du graphe :
-
-
À partir du point d’intersection de
la tangente à la courbe à t = 0 et de l’asymptote horizontale
de la courbe :
-
Valeur de τ :
-
τ.
≈ 8,0 ms b.
Méthode à 63 % de sa valeur maximale.
-
Au bout d’une durée τ après
l’établissement du courant, l’intensité est égale à 63 % de sa
valeur maximale.
-
À l’aide du graphique on en déduit la
valeur de τ.
-
-
Graphe :
-
τ ≈ 8,0 ms c.
L’intensité passe d’une valeur égale à 10 %
de sa valeur maximale à une valeur égale à 90 % de sa valeur
maximale sur une durée Δt = 2,2 τ.
-
À l’aide du graphique, on en déduit
la valeur de τ.
-
Δt = 2,2 τ ≈ 17 ms
-
τ ≈ 7,7 ms d.
Comparaison :
-
On trouve sensiblement les mêmes
valeurs. 3.
Valeur de l’inductance L de la
bobine.
-
R = 11 Ω
-
4.
Valeur
-
5.
Valeur de la f.é.m. e aux bornes de
la bobine au temps t = 0.
-

![]()
![]() où A, B et k
sont des constantes.
où A, B et k
sont des constantes.
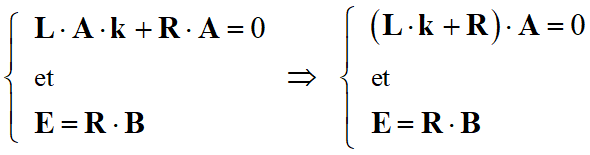
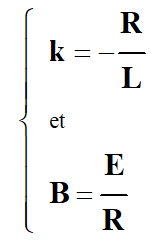
![]()

![]() .
.

![]()
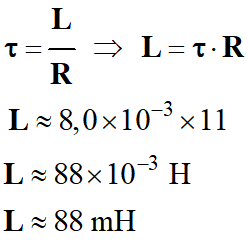
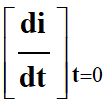 :
:
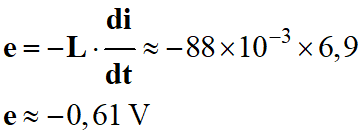
![]()
4)- Exercice 15 : Énergie emmagasinée dans une bobine :
|
Énergie emmagasinée dans une bobine : 1.
Donner l’expression de l’énergie emmagasinée
par une bobine d’inductance L, parcourue par un courant
d’intensité i. 2. Une bobine a une inductance L = 0,80 H. elle est parcourue par un courant d’intensité i = 40 mA. Calculer l’énergie emmagasinée par cette bobine. 3.
Que devient cette énergie lors de
l’ouverture du circuit ? |
Énergie emmagasinée dans une bobine : 1.
Expression de l’énergie emmagasinée par une
bobine.
Em
= WL
Énergie en joule (J)
L
Inductance en henry (H)
i
Intensité en ampère (A) 2.
Énergie emmagasinée par cette bobine. 3.
Énergie lors de l’ouverture du circuit :
-
Bobine d’inductance L :
-
Courant d’intensité i :
-
Une bobine d'inductance
L,
traversée par un courant d’intensité
i,
emmagasine de l'énergie.
-
C'est de l'énergie magnétique que
l'on note
![]()
-
L’intensité du courant électrique
dans un circuit comportant une bobine ne subit pas de discontinuité.
-
Le courant s’établit de façon
progressive et s’annule de la même façon.
-
L’intensité du courant électrique ne
peut pas passer de façon instantanée de la valeur zéro à la valeur
I.
-
Inductance L = 0,80 H.
-
Elle est parcourue par un courant
d’intensité :
-
i = 40 mA
-
Application numérique :
-
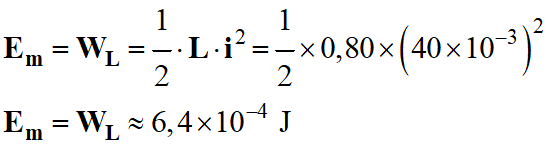
-
Lors de l’ouverture du circuit, cette
énergie est dissipée vers le milieu extérieur sous forme d’effet
Joule.
![]()
5)- Exercice 19 : Exploitation d’expérience :
|
Exploitation d’une expérience : On a réalisé le montage du schéma suivant : Montage :
À l’aide de l’ordinateur, on a enregistré la variation au cours
du temps des tensions : uAN = uPN et uBN
= R . i. On a obtenu les courbes ci-dessous : Graphe : La résistance R vaut 100 Ω. En utilisant les courbes obtenues, répondre aux questions
suivantes : 1.
Indiquer la valeur de la f.é.m. E de
la pile. 2.
Justifier graphiquement que la pile possède
une résistance interne ? 3.
La bobine possède-t-elle une résistance
propre r ? Justifier la réponse. 4.
Lorsque le courant permanent est établi : a.
Que vaut la f.é.m. d’auto-induction e ? b.
Écrire la loi d’Ohm pour chaque dipôle ; c.
Exprimer E en fonction de ρ,
R, r et I. 5.
Déterminer les valeurs de : a.
L’intensité I ; b.
La résistance interne ρ de la pile ; c.
De la résistance propre r de la
bobine. 6.
Évaluer : a.
La constante de temps τ du circuit ; b.
L’inductance L de la bobine : c.
L’énergie emmagasinée par la bobine en
régime permanent. |
|
Exploitation d’une expérience : 1.
Valeur de la f.é.m. E de la pile.
-
E = uPN au
temps t = 0.
-
La lecture graphique donne :
-
E ≈ 4,30 V 2.
La pile possède une résistance interne :
-
Justification graphique :
-
La pile possède une résistance
interne ρ car en régime permanent :
-
E > uPN. 3.
Résistance propre r de la bobine :
-
La bobine possède une résistance
interne r car en régime permanent :
-
uPN = uAN>
uBN 4.
Lorsque le courant permanent est établi :
-
En régime permanent : i = I
= cte a.
Valeur de la f.é.m. d’auto-induction e :
-
En courant permanent :
-
b.
Loi d’Ohm pour chaque dipôle :
-
Loi d’ohm aux bornes de la source de
courant (E, ρ) :
-
uPN = E -
ρ . i
-
uPN = E -
ρ . I
-
Loi d’ohm aux bornes de la bobine (L,
r) :
-
-
Loi d’Ohm aux bornes du conducteur
ohmique de résistance R :
-
uBN = R .
i
-
uBN = R .
I c.
Expression de E en fonction de ρ,
R, r et I.
-
En régime permanent : i = I.
-
uPN = uPB
+ uBN = uAB + uBN
-
E - ρ . I= r
. I + R . I
-
E = (ρ + r +
R) . I 5.
Déterminer les valeurs de : a.
Valeur de l’intensité I : - Pour déterminer la valeur de l’intensité I dans le circuit, en régime permanent, on détermine par exploitation graphique, la valeur de la tension
uPN (voie 1) :
-
Exploitation graphique : - Lorsque le courant permanent d’intensité I est établi, on peut mesurer la tension aux bornes des différents dipôle :
-
uPN = E -
ρ . I ≈ 4,04 V
-
uBN = R .
I ≈ 3,77 V - Connaissant la valeur de la résistance R du conducteur ohmique, on peut en déduire la valeur de l’intensité I en régime
permanent :
-
b.
Valeur de la résistance interne ρ de
la pile :
-
uPN = E -
ρ . I ≈ 4,04 V
-
c.
Valeur de la résistance propre r de
la bobine :
-
uAB = uAN
– uBN
-
En régime permanent :
-
uAB = r .
I
-
6.
Évaluer : a.
Valeur de la constante de temps τ du
circuit : - Pour déterminer graphiquement la valeur de τ, on trace la tangente à l’origine à la courbe uBN = g (t) et l’asymptote horizontale à cette courbe.
-
L’abscisse du point d’intersection de
ces deux droites donne la valeur de la constante de temps τ.
-
D’autre part : - Au bout d’une durée τ après l’établissement du courant, l’intensité est égale à 63 % de sa valeur maximale.
-
À l’aide du graphique on en déduit la
valeur de τ.
-
-
En conséquence :
-
uBN
(τ) = 0,63 R . I
-
uBN (τ) =
0,63 × 100 × 3,77 × 10–2
-
uBN (τ) ≈
2,38 V
-
uBN (τ) ≈
2,4 V
-
Exploitation du graphe :
-
τ ≈ 13 ms b.
Valeur de l’inductance L de la
bobine :
-
c.
Énergie emmagasinée par la bobine en régime
permanent.
-
C'est de l'énergie magnétique que
l'on note
-
|
||||||||
6)- Exercice 16 : Inductance d’une bobine :
|
Inductance d’une bobine : L’inductance d’une bobine longue est donnée par la formule :
Avec : N : le nombre de spires ; ℓ : longueur du solénoïde en mètre (m) ; S : La surface d’uns spire ; μ0 = 4 π
× 10–
7 S.I (Henry / mètre : H / m). Soit un solénoïde (A, C) de résistance négligeable,
de longueur ℓ = 1,0 m. Il comporte N = 1000 spires circulaires de rayon r
= 5,0 cm. Le sens de l’orientation pour l’intensité est choisi de A
vers C dans le solénoïde. 1.
Il est parcouru par un courant d’intensité
i = 5,0 A. a.
Schématiser l’enroulement du solénoïde. b. Donner les caractéristiques du champ magnétique créé dans la région centrale du solénoïde par le passage du courant. Proposer des expériences
permettant de déterminer ces caractéristiques. c.
Calculer la valeur de L. 2. Ce solénoïde est maintenant parcouru par un curant dont l’intensité i (t) varie avec le temps comme
l’indique la figure ci-dessous.
Un phénomène d’auto-induction prend naissance dans le solénoïde dont les bornes A et C sont reliées à un oscilloscope afin de visualiser la tension uAC. a.
Donner l’expression de la tension uAC
au cours des deux phases pour t variant de 0 à 50 ms. b. Tracer la courbe uAC (t) visualisée à l’oscilloscope sachant que la basse de temps est réglée sur 10 ms . div–1. |
|
Inductance d’une bobine : L’inductance d’une bobine longue est donnée par la formule :
Avec : N : le nombre de spires ; ℓ : longueur du solénoïde en mètre (m) ; S : La surface d’uns spire ; μ0 = 4 π
x 10–
7 S.I (Henry / mètre : H / m). 1.
Il est parcouru par un courant d’intensité
i = 5,0 A. a.
Schéma l’enroulement du solénoïde.
-
Schéma : b.
Caractéristiques du champ magnétique créé
dans la région centrale du solénoïde.
►
Champ magnétique à l’intérieur d’un
solénoïde. (TP Physique N° 2)
-
Le champ magnétique à
l’intérieur d’un solénoïde est pratiquement uniforme.
-
Les lignes de champ à
l’intérieur du solénoïde sont des droites parallèles.
-
Caractéristiques du vecteur
champ magnétique
-
Remarques : La perméabilité
de l’air est voisine de celle du vide :
μ =
μ0 . μr
-
Pour l’air : μr ≈
1,0 4.
-
Pour le fer doux : μr =
1 +
χ m avec
-
μr perméabilité
relative et
χ m susceptibilité magnétique.
-
Expériences permettant de déterminer
ces caractéristiques :
-
On peut utiliser un teslamètre
(associé à une sonde de Hall).
TP
Physique
N° 02 : c.
Valeur de l’inductance L.
-
-
Application numérique :
-
2.
Un phénomène d’auto-induction.
a.
Expression de la tension uAC
au cours des deux phases.
-
Loi d’Ohm aux bornes d’une bobine :
-
Schéma :
-
-
Si la valeur de la résistance est
négligeable (devant les autres valeurs) :
-
-
t € [0 ; 50 ms ] :
-
1ier phase : t €
[0 ; 40 ms] : phase ascendante
-
i =
a .
t avec a positif :
-
Valeur de
a : coefficient directeur
du segment de droite :
-
On en déduit la valeur de la tension
uAC dans
l’intervalle t € [0 ; 40 ms]
-
-
2ième phase : t €
[40 ; 50 ms] : phase ascendante
-
i =
a’ .
t + b’ avec a’ négatif :
-
Valeur de
a’ : coefficient
directeur du segment de droite :
-
b.
Courbe uAC (t)
visualisée à l’oscilloscope.
-
Basse de temps
b = 10 ms . div–1
-
Sensibilité verticale :
k = 0,5 V . div–1
-
Sensibilité horizontale : b = 10 ms . div–1 |
|
|