Pour se défendre, les fourmis utilisent deux moyens :

Leurs mandibules, qui immobilisent l’ennemi, et la projection d’acide formique qui provoque des brûlures.

L’équation de la réaction, associée à cet équilibre est :

Le pH d’une solution d’acide formique de volume V = 50,0 mL

et de concentration molaire apportée C = 1,0 x 10^–3 mol . L^–1 vaut 3,5.

1)- Établir le tableau d’avancement de la réaction.

2)- Déterminer l’avancement maximal x_max.

3)- Calculer l’avancement final x_f  de la réaction.

4)- Comparer x_f et x_max. Conclure.

5)- Calculer les quantités de matières des espèces chimiques dans l’état d’équilibre final.

1)- Tableau d’avancement de la réaction.

2)- Avancement maximal x_max.

-  L’eau étant le solvant, elle est en large excès.

-  L’acide méthanoïque est le réactif limitant.

-  n – x_max = 0

-  x_max = n ≈ 5,0 x 10^–5 mol

3)- Avancement final x_f de la réaction.

-  D’après le tableau d’avancement de la réaction : x_f = n_éq (H₃O⁺)

-  On connaît la valeur du pH de la solution :

-  pH = 3,5

-  Par définition :

-  pH  = - log [H₃O⁺]_éq cette relation est équivalente à [H₃O⁺] _éq = 10^{– pH} mol . L^–1

-  [H₃O⁺] _éq = 10^{– 3,5} mol . L^–1 

-  Avec : n_éq (H₃O ⁺) = [H₃O⁺] _éq . V

-  x_f = n_éq (H₃O ⁺) = [H₃O⁺] _éq . V ≈ 10^{– 3,5} . 50,0 x 10^–3 mol

-  x_f ≈ 1,6 x 10^–5 mol

4)- Comparaison x_f et x_max et conclusion :

-  x_f  <  x_max, la réaction n’est pas totale, elle est limitée.

-  On atteint un équilibre chimique.

-  L’acide méthanoïque n’est pas totalement dissocié dans l’eau :

-  C’est un acide faible.

5)- Quantités de matières des espèces chimiques dans l’état d’équilibre final.

Une solution aqueuse S d’acide bromhydrique est obtenue en faisant réagir

du bromure d’hydrogène avec de l’eau, selon la réaction d’équation :

Le pH de la solution S,

sa concentration molaire C en soluté apporté

et son volume  V valent respectivement :

-  pH = 2,6 ; C = 2,51 x 10^–3 mol . L^–1  et V = 50,0 mL.

1)- Établir le tableau d’avancement de la réaction.

2)- Calculer l’avancement maximal x_max, puis l’avancement final x_f de la réaction.

3)- La réaction étudiée est-elle totale ?

  Comment cela se traduit-il dans l’écriture de l’équation de la réaction.

1)- Tableau d’avancement de la réaction.

2)- Avancement maximal x_max et avancement final x_f de la réaction.

-  Avancement final :

-  L’eau étant le solvant, elle est en large excès. L’acide bromhydrique  est le réactif limitant.

-  n – x_max = 0

-  x_max = n ≈ 1,26 x 10^–4 mol ≈ 1,3 x 10^–4 mol (si on garde deux chiffres significatifs)

-  Avancement final :

-  On connaît la valeur du pH de la solution :

-  pH = 2,6

-  Par définition :

-  pH  = - log [H₃O⁺]_éq cette relation est équivalente à [H₃O⁺] _éq = 10^{– pH} mol . L^–1

-  [H₃O⁺] _éq = 10^{– 2,6} mol . L^–1 

-  Avec : n_éq (H₃O ⁺) = [H₃O⁺] _éq . V

-  x_f = n_éq (H₃O ⁺) = [H₃O⁺] _éq . V ≈ 10^{– 2,6} . 50,0 x 10^–3 mol

-  x_f ≈ 1,3 x 10^–4 mol

-  Comme la quantité de matière a été déterminée à partir d’une valeur de pH,

-  on ne peut donner le résultat qu’avec deux chiffres significatifs.

-  On remarque que x_max ≈ x_f.

3)- Réaction totale.

-  x_max = n ≈ 1,26 x 10^–4 mol ≈ 1,3 x 10^–4 mol (si on garde deux chiffres significatifs)

-  x_f ≈ 1,3 x 10^–4 mol

-  La réaction est totale car x_max = x_f  (au nombre de chiffres significatifs près)

-  La molécule de bromure d’hydrogène n’existe pas en solution aqueuse.

-  La réaction entre le bromure d’hydrogène et l’eau s’écrit avec une flèche dans le sens direct.

-  Remarque : on est en présence d’un acide fort : pH = – log C, avec 10 ^–2 mol . L^–1 ≤ C ≤ 10 ^–6 mol . L^–1

 L’aniline réagit avec l’eau selon la réaction d’équation :

1)- Identifier les deux couples acide / base associés à la réaction.

2)- L’aniline est-elle un acide faible ou une base faible dans l’eau ?

3)- Montrer que la réaction acido-basique précédente s’interprète comme l’échange d’un proton entre deux espèces appartenant à deux couples acide / base différents.

1)- Identification les deux couples acide / base associés à la réaction.

-  Couples (1) : H₂O _(ℓ) / HO ^– _(aq)

-  Couples (2) : C₆H₅NH₃⁺ _(aq) / C₆H₅NH_{2 (aq)}

2)- L’aniline une base faible dans l’eau :

-  D’après l’équation donnée, on remarque qu’il y a une double flèche :

-  Cela indique que la réaction entre l’aniline est l’eau n’est pas totale.

-  On est en présence d’un équilibre chimique.

-  De plus la réaction donne des ions hydroxyde HO ^– _(aq).

-  L’aniline est une base faible dans l’eau.

-  Formule de l’aniline :

3)- Étude de la réaction acido-basique :

Un comprimé effervescent contient entre autres, de l’acide acétylsalicylique (ou aspirine), C₉H₈O₄,

 et de l’hydrogénocarbonate de sodium, NaHCO₃.

l’ion hydrogénocarbonate, HCO₃^– (aq), est une base faible dans l’eau.

1)- Écrire l’équation de la réaction qui se produit entre l’aspirine et l’eau.

2)- Écrire l’équation de dissolution de l’hydrogénocarbonate de sodium dans l’eau, en la considérant comme totale.

3)- L’acide conjugué de l’ion hydrogénocarbonate HCO₃^– (aq) est le dioxyde de carbone dissous CO₂, H₂O (aq).

Écrire l’équation de la réaction qui se produit entre l’ion hydrogénocarbonate et l’aspirine.

4)- Justifier l’effervescence observée lors de la dissolution du comprimé dans l’eau.

Pour aller plus loin :  Formulation et dosage de l’Aspirine. Effet Tampon

1)- Équation de la réaction qui se produit entre l’aspirine et l’eau.

-  L’aspirine est un acide faible dans l’eau. On arrive à un équilibre chimique (double flèche).

2)- Équation de dissolution de l’hydrogénocarbonate de sodium dans l’eau, en la considérant comme totale.

-  Réaction totale : une simple flèche dans le sens direct.

3)- Équation de la réaction qui se produit entre l’ion hydrogénocarbonate et l’aspirine.

4)- Effervescence observée lors de la dissolution du comprimé dans l’eau.

-  En milieu acide, les ions hydrogénocarbonate se transforment en dioxyde de carbone.

-  La solubilité du dioxyde de carbone dans l’eau à 25 °C est de l’ordre de 0,1 mol / L.

-  La limite de solubilité est très vite atteinte et on observe un dégagement gazeux de dioxyde de carbone.

Pour aller plus loin :  Formulation et dosage de l’Aspirine. Effet Tampon

1)- Tableau d’avancement :

2)- Quantité de matière initiale d’eau notée n₀.

-   

3)- Valeur de l’avancement maximal x_max.

-  L’avancement total est atteint lorsque l’eau a été totalement consommée :

-   

4)- Valeur de l’avancement final x_f.

-  On connaît la valeur du pH de la solution :

-  pH = 7,0

-  Par définition :

-  pH  = - log [H₃O⁺]_éq cette relation est équivalente à [H₃O⁺] _éq = 10^{– pH} mol . L^–1

-  [H₃O⁺] _éq = 10^{– 7,0} mol . L^–1 

-  Avec : n_éq (H₃O ⁺) = [H₃O⁺] _éq . V

-  x_f = n_éq (H₃O ⁺) = [H₃O⁺] _éq . V ≈ 10^{– 7,0} x 1,0 mol

-  x_f ≈ 1,0 x 10^–7 mol

-  Comme la quantité de matière a été déterminée à partir d’une valeur de pH,

-  On ne peut donner le résultat qu’avec deux chiffres significatifs.

5)- Comparer x_f et x_max. Conclure.

-  x_f ≈ 1,0 x 10^–7 mol et x_max ≈ 28 mol.

-  x_f << x_max

-  Le nombre de molécules d’eau dissociées est très faible.

-  La réaction est très limitée dans le sens direct.

-  On est en présence d’un équilibre chimique.

-  La réaction est quasi totale dans le sens inverse (réaction acido-basique).

Chap N° 05 Réactions acido-basiques (programme 2002)

1)- Valeur du pK_A associé au couple acide / base.

-  Par définition : pK_A = – log K_A,   soit   K_A = 10^{– pKA}

-  pK_A = – log K_A = – log (6,3 x 10^–10)

-  pK_A = 9,2

2)- Diagramme de prédominance correspondant.

3)- Le pH d’une solution aqueuse d’ammoniac vaut 10,6.

a)-  Espèce prédominante dans la solution :

-  Dans ce cas pH > pK_A, l’espèce qui prédomine est l’ammoniac NH₃ (aq)

-  Avec le diagramme de prédominance :

b)-  Valeur du quotient  :

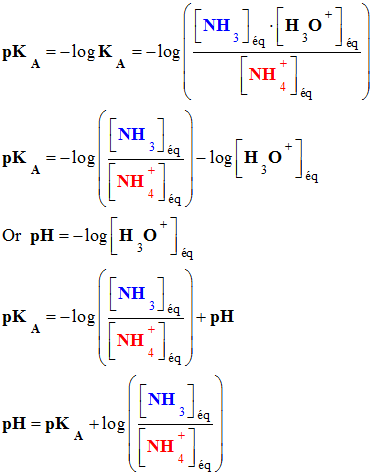
-  On utilise la relation : Additif (pour retrouver la relation)

- 

-   

c)-  Le résultat obtenu est en accord avec la réponse à la question 3)- a)- :

-  NH₃ prédomine devant NH₄⁺

Additif : Pour retrouver la relation

-  Étude du couple NH₄⁺ (aq) / NH₃ (aq) :

-  À ce couple est associée la réaction suivante :

-  On associe à cette réaction la constante d’acidité :

-   

-  En utilisant pK_A = – log K_A

-   

L’acide nitrique HNO₃ (ℓ) est un acide fort dans l’eau.

de concentration molaire en soluté apporté C = 2,5 x 10^–3 mol . L^–1.

1)- Définir un acide fort dans l’eau.

2)- Écrire l’équation de la réaction entre l’acide nitrique HNO₃ (ℓ) et l’eau.

3)- Calculer le pH de la solution S.

4)- On dilue dix fois la solution S : on obtient une solution S’.

  Quel est le pH de la solution S’ ?

1)- Définition un acide fort dans l’eau.

-  Un acide AH est fort dans l’eau si sa réaction avec l’eau est totale.

-  L’équation de cette réaction s’écrit alors avec une simple flèche :

2)- Équation de la réaction entre l’acide nitrique HNO₃ (ℓ) et l’eau.

3)- Valeur du pH de la solution S.

-  Le pH d’une solution diluée d’acide fort, de concentration C en soluté apporté, est :

-  La valeur de la concentration C = 2,5 x 10^–3 mol . L^–1 appartient bien au domaine de validité :

-  pH = – log C = – log (2,5 x 10^–3)

-  pH ≈ 2,6

4)- Valeur du pH de la solution S’ ?

-  On a effectué une dilution :

-  C’ = C / 10

-  C’= 2,5 x 10^–4 mol . L^–1

-  La valeur de la concentration C’ = 2,5 x 10^–4 mol . L^–1 appartient bien au domaine de validité :

-  pH = – log C = – log (2,5 x 10^–4)

-  pH ≈ 3,6

Une solution aqueuse S d’hydroxyde de sodium est préparée par dissolution totale du solide NaOH (s).

La solution obtenue est une solution de base forte de concentration C = 5,0 x 10^–2 mol . L^–1.

1)- Écrire l’équation de la dissolution.

2)- Calculer le pH de la solution S.

3)- On dilue dix fois la solution S : on obtient une solution S’. Quel est le pH de la solution S’ ?

1)- Équation de la dissolution.

-  La réaction de dissolution de l’hydroxyde de sodium NaOH (s) est une réaction totale dans l’eau.

-  Solution aqueuse d’hydroxyde de sodium :

NaOH (s) + H₂O (ℓ)  →  (Na⁺, H₂O) (aq)  +  OH^– (aq)

-  Cela revient à la dissolution d’un composé ionique dans l’eau que l’on peut écrire plus simplement :

-  formule de la soude : {Na⁺ (aq) + HO^– (aq)} (solution aqueuse d’hydroxyde de sodium)

2)- Valeur du pH de la solution S.

-  Une base A^– est forte dans l’eau si sa réaction avec l’eau est totale.

-  L’équation de cette réaction s’écrit alors avec une simple flèche :

-  Le pH d’une solution diluée de base forte, de concentration C en soluté apporté, est :

-  La valeur de la concentration C = 5,0 x 10^–2 mol . L^–1appartient bien au domaine de validité :

-  pH = 14 + log C = 14 + log (5,0 x 10^–2)

-  pH ≈ 12,7

-  pH ≈ 13

3)- Valeur du pH de la solution S’

-  On a effectué une dilution :

-  C’ = C / 10

-  C’= 5,0 x 10^–3 mol . L^–1

-  La valeur de la concentration C’ = 2,5 x 10^–4 mol . L^–1 appartient bien au domaine de validité :

-  pH = 14 + log C = 14 + log (5,0 x 10^–3)

-  pH ≈ 11,7

-  pH ≈ 12

1)- Le pH-mètre :

a)-  Réglage du pH-mètre :

étalonnage du pH-mètre

-  Il est nécessaire d’étalonner le pH-mètre avant toute mesure.

-  L’étalonnage du pH-mètre nécessite l’utilisation de deux solutions étalons (solutions tampons) de pH connu.

-  Il faut régler aussi le bouton température sur la valeur de la température de la solution.

b)-  Les solutions utilisées :

-  Solutions étalons (pH₁ = 4,00 ; pH₂ = 7,00)

2)- Incertitude de la mesure donnée par le pH-mètre :

-  pH_solution = pH_mesuré ± U (pH)

-  pH_solution = 2,52 ± 0,05

3)- Encadrement de la concentration [H₃O⁺]_solution correspondante et l’incertitude U ([H₃O⁺]).

-  De la relation :

-  pH_solution = 2,52 ± 0,05

-  On tire : Encadrement de la valeur du pH

2,47  ≤  pH_solution ≤  2,57

-  Par définition : [H₃O⁺] = 10^{– pH} mol . L^–1

-  [H₃O⁺]_mesuré = 10^{– 2,52} mol . L^–1

-  [H₃O⁺]_mesuré  ≈ 3,02 x 10^–3 mol . L^–1 (avec 3 chiffres significatifs)

-  Par définition :  pH = – log [H₃O⁺]

2,47  ≤  pH_solution ≤  2,57

2,47  ≥  log [H₃O⁺]_solution  ≥  2,57

-  Comme la fonction logarithme décimal est une fonction croissante :

x₁ < x₂ Þ log x₁ < log  x₂

et

log a ≤  log x ≤ log b Þ 10^a ≤   x  ≤ 10^b

-  On obtient :

10^{– 2,47} mol . L^–1 ≥  [H₃O⁺]_solution  ≥ 10^{– 2,57} mol . L^–1

3,39 x 10^–3 mol . L^–1 ≥  [H₃O⁺]_solution  ≥ 2,69 x 10^–3 mol . L^–1

2,69 x 10^–3 mol . L^–1 ≤  [H₃O⁺]_solution  ≤  3,39 x 10^–3 mol . L^–1

-  Incertitude sur la valeur de la concentration [H₃O⁺]_solution de la solution :

-  L’incertitude U ([H₃O⁺] = 0,35 x 10^–3  mol . L^–1

-  [H₃O⁺] _solution  = (3,04 ± 0,35) x 10^–3  mol . L^–1

4)- Valeur de l’incertitude relative :

-  Valeur de l’incertitude sur la mesure du pH :

-   

-  Valeur de l’incertitude relative sur la valeur de la concentration [H₃O⁺]_solution :

-   

-  Une incertitude relative d’environ 2 % sur la valeur du pH entraîne une incertitude relative d’environ 10 % (plus de 5 fois plus) sur celle de la concentration [H₃O⁺]_solution.

-  Cela provient du fait que l'on utilise une échelle logarithmique (logarithme décimal)

5)- La concentration [H₃O⁺]_solution et chiffres significatifs :

-  Conséquence :

Une mesure de pH effectuée à 0,05 unité près conduit à une valeur de la concentration [H₃O⁺] connue à 11,5 % près.

Une simple mesure de pH ne peut donner une concentration avec précision.

-  Il faut limiter le nombre de chiffres significatifs pour représenter une concentration déduite de la valeur du pH.

-  Toute concentration déduite de la valeur du pH sera exprimée avec :

 2 chiffres significatifs au maximum .

-  Dans le cas présent, on donne :

-  [H₃O⁺]_solution  ≈ 3,0 x 10^–3 mol . L^–1