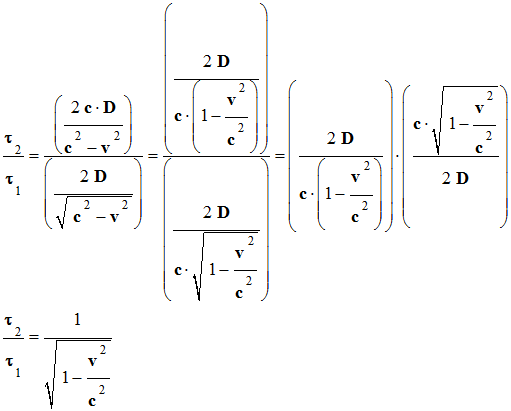|
Chap. N° 08 |
Relativité restreinte. Cours. |
|
|
|
|
Exercices : énoncé avec corretion a)- Exercice 9 page 219 : étudier un électron dans un tube cathodique d’un téléviseur. b)- Exercice 11 page 220 : exploiter la relation entre durée propre et
durée mesurée. c)- Exercice 15 page 220 : une période variable. d)-
Exercice 18 page 222 : Expérience de Bertozzi e)- Exercice 20 page 223 : Quand les durées se dilatent.
f)-
Exercice 26 page 225 : L’énergie relativiste. |
I-
Invariance de la vitesse de la lumière dans le vide.
-
Dans un référentiel terrestre supposé galiléen, on
considère deux voitures A et
B :
►Première
situation :
-
La voiture A est animée d’un mouvement rectiligne
uniforme de vitesse
-
vA = 60 km / h
-
Direction : droite (AB)
-
Sens de A vers
B
-
La voiture B est animée d’un mouvement rectiligne
uniforme de vitesse
-
vB = 50 km / h
-
Direction : droite (AB)
-
Sens de B vers
A
![]() Questions :
Questions :
-
Faire le schéma de la situation.
-
Donner les caractéristiques du mouvement de la voiture
A par rapport à la voiture
B.
-
Que peut-on dire de la vitesse de la voiture
A par
rapport à la voiture B ?
![]() Réponses :
Réponses :

-
La voiture A est animée d’un mouvement rectiligne
uniforme par rapport à la voiture B (référentiel d’étude)
-
La valeur de la vitesse :
-
vA/B =
vA + vB
-
vA/B = 110 km / h
-
Direction : droite (AB)
-
Sens : de A vers
B.
►Deuxième
situation :
-
La voiture A est animée d’un mouvement rectiligne
uniforme de vitesse
-
vA = 60 km / h
-
Direction : droite (AB)
-
Sens de A vers
B
-
La voiture B est animée d’un mouvement rectiligne
uniforme de vitesse
-
vB = 50 km / h
-
Direction : droite (AB)
-
Sens de A vers
B
![]() Questions :
Questions :
-
Faire le schéma de la situation.
-
Donner les caractéristiques du mouvement de la voiture
A par rapport à la voiture
B.
-
Que peut-on dire de la vitesse de la voiture
A par
rapport à la voiture B ?
![]() Réponses :
Réponses :

-
La voiture A est animée d’un mouvement rectiligne
uniforme par rapport à la voiture B (référentiel d’étude)
-
La valeur de la vitesse :
-
vA/B =
vA – vB
-
vA/B = 10 km / h
-
Direction : droite (AB)
-
Sens : de A vers
B.
►Conclusion :
-
Dans la mécanique classique, les règles de composition
des vitesses s’appliquent.
-
On peut appliquer les mêmes règles de composition
(addition ou soustraction) des vitesses si on remplace une
voiture par un signal sonore.
-
Maintenant, on va remplacer une voiture par un signal
lumineux.
2)- Expérience de Michelson et
Morley.
-
Le caractère ondulatoire de la lumière a été mis en
évidence au XIXe siècle grâce aux phénomènes de
diffraction et d’interférences.
-
On pense alors que comme pour les ondes mécaniques, la
lumière nécessite un milieu de propagation.
-
Ce milieu de propagation est appelé « éther », fluide
immobile qui remplit tout l’espace.
-
Dans ce milieu, la lumière se propagerait à vitesse
constante.
-
La Terre en mouvement par rapport à cet « éther » serait
soumise à un « vent d’éther » de sens opposé à celui de son
déplacement.
-
Schéma :
-
A. Michelson (1852-1931) et E. Morley (1838-1923) ont
conçu un appareil, l’interféromètre.
-
Le but de l’expérience était de mesurer la vitesse de
déplacement de la Terre par rapport à cet éther hypothétique.
-
Les deux physiciens ont fait une découverte inattendue.
b)-
Le dispositif : l’interféromètre.
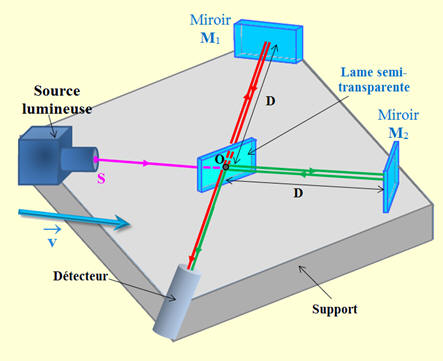
-
Le référentiel d’étude est le référentiel héliocentrique
supposé galiléen.
-
On note c la vitesse de propagation de la lumière
dans le référentiel héliocentrique.
-
On considère que le référentiel du laboratoire
(référentiel terrestre) se déplace d’un mouvement rectiligne
uniforme de vitesse v = 3,0
× 104 m / s par rapport au référentiel
héliocentrique, ceci pendant la durée de l’expérience.
-
Le référentiel du laboratoire est galiléen.
-
La lumière émise par la source
S rencontre en
O
le miroir semi-transparent.
-
Une partie de la lumière est réfléchie vers le miroir
M1
-
L’autre partie traverse, le miroir semi-transparent, sans
être déviée en direction du miroir M2.
-
Après réflexion, en incidence nulle respectivement sur
les miroirs M1 et
M2, le
même phénomène se produit sur le miroir semi-transparent.
-
Le détecteur permet d’observer le phénomène
d’interférence entre les rayons ayant suivi les deux trajets
représentés en rouge et en vert.
-
On se place dans le cas où le support de ce dispositif,
fixe sur la Terre, est orienté de telle sorte que l’axe
SOM2
est parallèle à la direction de la vitesse du support par
rapport au référentiel héliocentrique.
-
En conséquence, la lumière émise par la source
S
se propage dans le même sens que de
O vers
M2,
mais de sens contraire de M2 vers
O.
-
En utilisant la règle de composition des vitesses (comme
on l’a fait pour les voitures), on peut dire que :
-
Par rapport au support,
-
La lumière effectue le trajet aller de
O vers
M2
à la vitesse : va =
c – v
-
La lumière effectue le trajet retour de
M2
vers O à la vitesse
vr =
c +
v
-
La direction OM1 est perpendiculaire au
vecteur vitesse
 , le
trajet OM1O est moins affecté par le
mouvement.
, le
trajet OM1O est moins affecté par le
mouvement.
![]() Calculer
la durée τ1 pour effectuer le trajet
OM1O
Calculer
la durée τ1 pour effectuer le trajet
OM1O
![]() Calculer
la durée τ2 pour effectuer le trajet
OM2O :
Calculer
la durée τ2 pour effectuer le trajet
OM2O :
-
Schéma 1 et 2 :
- On travaille dans le référentiel héliocentrique.
- Le
support se déplace d’un mouvement rectiligne uniforme de vitesse
v comme indiqué sur le schéma.
-
La durée τ1 :

-
Aller :
-
On note τa1la durée nécessaire au rayon
rouge pour parcourir la distance OM1.
-
Pendant cette durée, le miroir semi-réfléchissant s’est
déplacé de la distance :
-
OO’ =
τa1 .
v
-
Le rayon parcourt la distance
OM1 à la
vitesse c :
-
OM1 =
c .
τa1
-
En utilisant le théorème de Pythagore, on écrit :
-
(c .
τa1)2 = (D)2
+ (τa1 .
v)2
-
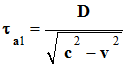
-
Retour :
-
On note τr1
la durée nécessaire au rayon
rouge pour parcourir la distance M1O’’.
-
De la même façon, on trouve :
-

-
La durée τ1 :
-

-
Si on compare les valeurs de
c = 3,0
× 108 m / s et
v = 3,0
× 104 m / s, on remarque que :
-
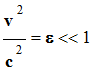
-
On utilise la relation : (1 – ε)n ≈ 1 – n .
ε
-
On tire :
-
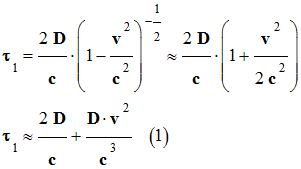
-
La durée τ2 :
-
Schéma :

-
Aller :
-
On note τa2
la durée nécessaire au
rayon vert pour parcourir la distance OM’2.
-
OM’2 =
D +
τa2
. v
-
OM’2 =
c .
τa2
-

-
Retour :
-
On note τr2
la durée nécessaire au
rayon vert pour parcourir la distance M’2O’’.
-
M’2O’’=
c .
τr2
= D –
τr2 .
v
-

-
La durée τ2 :
-

-
En faisant la même approximation que précédemment :
-

![]() En
déduire la différence de durée τ entre les trajets
OM2O
et OM1O
En
déduire la différence de durée τ entre les trajets
OM2O
et OM1O
-

![]() Donner
l’expression du rapport τ2 /
τ1.
Donner
l’expression du rapport τ2 /
τ1.
-
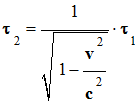
-
On note :
-
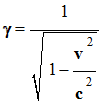
-
-
τ2 =
γ .
τ1
![]() Calculer
la valeur de τ sachant que :
Calculer
la valeur de τ sachant que :
-
D = 10 m ;
c = 3,0
× 108 m / s et
v = 3,0
× 104 m / s,
-
Valeur de τ :
-
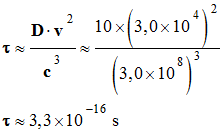
![]() Comparer
cette valeur à la période d’une radiation de longueur d’onde
dans le vide λ = 500 nm.
Comparer
cette valeur à la période d’une radiation de longueur d’onde
dans le vide λ = 500 nm.
![]() Justifier
l’utilité d’un dispositif d’interférences pour mesurer le
décalage attendu.
Justifier
l’utilité d’un dispositif d’interférences pour mesurer le
décalage attendu.
-
Relation fondamentale :
λ =
c . T
-

-
Comparaison :
-

-
Le décalage temporel,
τ ≈ 3,3
× 10–16
s, n’est pas mesurable directement, mais il entraîne un décalage
du système de franges de 1/5 de frange que l’on peut facilement
observer et mesurer.
►Observations
et conclusion :
-
Le calcul donne une différence 
-
Les deux faisceaux interfèrent et bien que la vitesse
v soit petite devant
c, la figure d’interférence
devrait être affectée d’une façon mesurable par cette différence
τ et dépendre de l’orientation de l’appareil par rapport
au vecteur vitesse
![]() , ce
qui n’a jamais été observé.
, ce
qui n’a jamais été observé.
-
Les expériences de Michelson et Morley devait mesurer
l’influence du déplacement de la Terre par rapport à l’éther,
mais elle a permis de mesurer l’influence du mouvement de la
Terre sur la vitesse de propagation de la lumière, mesurée dans
le référentiel terrestre.
-
On n’a jamais observé de décalage dans la figure
d’interférence.
-
En conséquence, la vitesse de la lumière mesurée sur la
Terre ne dépend pas du mouvement de celle-ci.
- L’échec de l’expérience de Michelson et Morley a permis de remettre en cause la mécanique classique (mécanique galiléenne et newtonienne) et a permis l’émergence d’une nouvelle théorie :
-
La relativité restreinte.
-
La relativité restreinte considère que la vitesse de la
lumière est invariante, c’est-à-dire que sa valeur ne dépend pas
du référentiel d’étude.
-
Ces deux théories ne sont pas incompatibles, car
l’application de la relativité restreinte à des systèmes à
faible vitesse permet de retrouver les conclusions de la
mécanique galiléenne.
3)- Insuffisance de la mécanique
classique :
-
Selon les lois classiques du mouvement, si deux mobiles
A et
B se déplacent avec des vitesses
![]() et
et
![]() par
rapport à un référentiel galiléen,
par
rapport à un référentiel galiléen,
-
Pour un passager de
A (référentiel), le véhicule
B (mobile) se déplace à la vitesse
![]()
-
Il en va de même si le mobile
B est remplacé par
une onde.
-
Cette loi de composition des vitesses ne s’applique pas
aux ondes lumineuses.
-
La mesure de la vitesse de propagation de la lumière dans
le vide par rapport à la Terre donne toujours la même valeur
c.
-
Cette valeur c est indépendante de la vitesse de
déplacement de la Terre par rapport au Soleil.
-
Tenant compte de ces résultats,
Albert Einstein publie
en 1905, une nouvelle théorie connue sous le nom de
relativité restreinte.
►Postulat
1 :
-
Les lois de la physique s’expriment de la même façon dans
tous les référentiels galiléens.
►Postulat
2 :
-
La vitesse de propagation de la lumière dans le vide est
indépendante du mouvement de la source lumineuse et elle est
invariante dans tout changement de référentiel galiléen.
►Conséquences :
-
Il existe une vitesse limite, égale à la célérité
c
de la lumière dans le vide.
-
Cette vitesse limite ne peut être dépassée par aucun et
signal et aucune particule.
-
Elle ne peut être atteinte que par les particules de
masse nulle comme le photon.
-
Un évènement est un phénomène objectif observable, c’est
un fait se produisant à un endroit donné.
-
Exemple d’évènement : un éclair, une explosion,
l’aiguille d’une horloge qui coïncide avec l’indication du
cadran, impulsion lumineuse, …
-
Pour repérer un évènement, il faut choisir un référentiel
et lui attribuer des coordonnées spatio-temporelle (x,
y,
z,
t).
b)-
Synchronisation des horloges.
►Un
exemple de synchronisation :
-
Pour synchroniser deux horloges fixes dans un même
référentiel, on peut procéder de la manière suivante :
-
Un observateur situé en
A de l’espace envoie une
impulsion lumineuse à la date tA
-
Puis une autre à la date
tA +
T0
où T0
est la période de l’horloge placée en
A.
-
Un observateur placé en
B de l’espace veut
synchroniser son horloge avec celle de l’observateur situé en
A.
-
L’observateur B ajuste la période de son horloge à
T0 à l’aide des signaux qui lui arrivent
-
Il renvoie le signal à l’aide d’un miroir
-
L’observateur A reçoit en retour les deux signaux
lumineux aux dates t’A et
t’A
+ T0
-
Pour régler l’heure, l’observateur
B note la date
d’arrivée du signal lumineux avec son horloge, détermine l’écart
avec la valeur
 que lui a
communiqué l’observateur A.
que lui a
communiqué l’observateur A.
-
Puis règle son horloge, si nécessaire, pour compenser
l’écart mesuré.

-
Le temps est une grandeur mesurée par une horloge.
►Cas de
la physique classique (Galilée et Newton).
- Le temps est absolu.
- Il est le même dans tout le
référentiel et dans tous les référentiels.
-
Le temps s’écoule indépendamment des conditions
extérieures.
-
Le temps s’écoule de la même façon pour tout observateur
qu’il soit immobile ou en mouvement par rapport à un référentiel
galiléen.
►Cas de
la relativité restreinte (Einstein).
-
Le temps dépend du référentiel d’étude.
-
Le temps ne s’écoule pas de la même façon pour tout
observateur.
-
La durée séparant deux évènements dépend du référentiel
d’étude.
►Cas des
horloges immobiles :
-
Deux horloges immobiles l’une par rapport à l’autre
mesurent les mêmes durées.
-
En conséquence :
tA2 –
tA1
= tB2 –
tB1
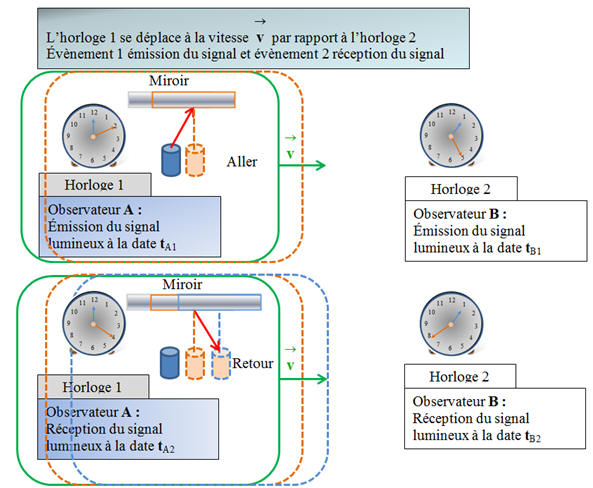
►Cas
d’horloge en mouvement par rapport à une autre horloge.
-
Une horloge en mouvement et une horloge fixe ne mesurent
pas les mêmes durées entre les évènements 1et 2.
-
On considère que le référentiel
A se déplace à la
vitesse
![]() par
rapport au référentiel B.
par
rapport au référentiel B.
-
Dans le référentiel
A :
-
Schéma :
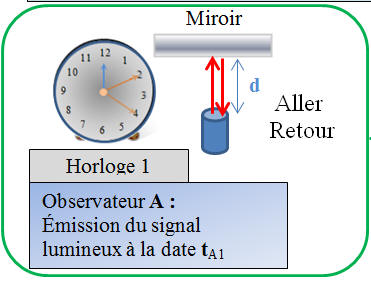
-
-
Dans le référentiel
B, l’observateur
B est
immobile et voit le référentiel (et l’horloge) se déplacer à la
vitesse 
-
Schéma :
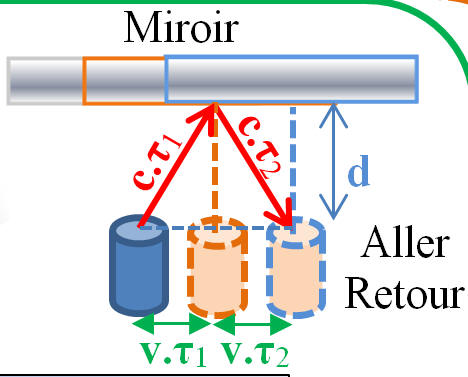
-
À l’aller, le signal arrive sur le miroir au bout de la
durée τ1 et met la durée
τ2
pour le retour.
-
Pendant la durée
τ1, l’ensemble s’est
déplacé de la distance (v .
τ1
-
En utilisant Pythagore, on peut écrire que :
-
(c .
τ1)2 =
d2
+ (v .
τ1)2
-
De même pour le retour, on écrit :
-
(c .
τ2)2 =
d2
+ (v .
τ2)2
-
On tire de ces expressions :
-

-
En conséquence :
-

-
ΔtB ≠
ΔtA
-
On peut calculer le rapport
ΔtB /
ΔtA
-

-
On note : 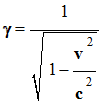 avec γ ≥ 1
avec γ ≥ 1
-
On remarque que :
ΔtB ≥
ΔtA
d)-
Notion de temps propre ou durée propre
-
Le terme temps propre a été introduit par Minkowski en
1908.
![]() La
durée propre ΔT0, est la durée séparant deux
évènements mesurés par une horloge fixe ayant lieu au même point
dans un référentiel galiléen (R).
La
durée propre ΔT0, est la durée séparant deux
évènements mesurés par une horloge fixe ayant lieu au même point
dans un référentiel galiléen (R).
-
Cette durée ΔT0 est mesurée par une
horloge fixe, proche des deux évènements dans le référentiel (R).
-
On utilise les termes de « temps propre » ou « durée
propre » (on préfère le terme « durée propre »).
-
Une durée propre concernant un objet est une durée
mesurée par une horloge immobile dans le référentiel propre à
cet objet.
e)-
Temps mesuré ou durée mesurée.
![]() La
durée mesurée ΔT’ est la durée séparant deux évènements
mesurés par une horloge fixe ayant lieu au même point dans un
référentiel galiléen (R’) en mouvement par rapport au
référentiel galiléen (R).
La
durée mesurée ΔT’ est la durée séparant deux évènements
mesurés par une horloge fixe ayant lieu au même point dans un
référentiel galiléen (R’) en mouvement par rapport au
référentiel galiléen (R).
-
Dans le référentiel (R), on mesure la
durée
propre.
-
Dans le référentiel (R’), on mesure la
durée
mesurée.
-
Le référentiel (R’) est en mouvement par rapport
au référentiel (R).
-
Les durées ΔT’ et
ΔT0 sont liées
par la relation de dilatation temporelle :
-
ΔT’ =
γ .
ΔT0
-
Le coefficient γ (gamma), sans unité, est donné
par la relation :
|
|
|
-
Remarques :
-
Deux horloges en mouvement relatif ne mesurent pas la
même durée entre deux évènements
-
ΔT’ ≥
ΔT0
-
C’est le phénomène de dilatation des durées.
-
Une horloge qui se déplace par rapport à un observateur
bat plus lentement qu’une horloge immobile par rapport à
l’observateur.
-
On considère une sonde spatiale se déplaçant à la vitesse
v = 1,0
× 105 m / s par rapport à un référentiel
terrestre supposé galiléen.
-
Quel est l’écart relatif
 entre la
durée propre et la durée mesurée dans le référentiel terrestre.
entre la
durée propre et la durée mesurée dans le référentiel terrestre.
-
Réponse :
-
ΔT’ ≥
ΔT0
-
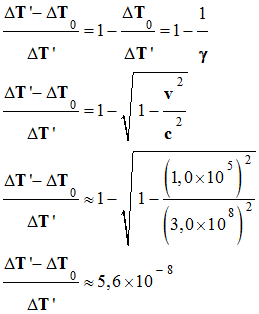
-
Lorsque la vitesse
v << c, la dilatation de temps
est imperceptible.
III- Physique classique et relativité restreinte.
1)- La vitesse
v est petite
devant c.
-
Le postulat d’Einstein est compatible avec les lois de la
mécanique classique de Galilée et Newton.
-
Si v <<
c, alors
γ ≈ 1 et
ΔT’
≈ ΔT0
-
Dans ce cas, la mesure de la durée est indépendante du
référentiel choisi.
-
Dans le cas où la valeur de la vitesse relative
v
entre les horloges est faible par rapport à la valeur de la
vitesse de propagation de la lumière dans le vide
c, la
dilatation des durées n’est plus perceptible, mais l’écart peut
être mesuré par les horloges atomiques actuelles.
-
Exemple :
- La mesure du temps dans un système de localisation (GPS) est d’une telle précision que la relativité du temps doit être prise en compte.
- La bonne marche d’un tel système valide la
théorie d’Einstein.
-
Sans synchronisation, les horloges embarquées dans les
satellites de localisation (GPS) seraient décalées par
rapport à l’horloge terrestre.
2)- La vitesse
v est voisine
de c.
- Les physiciens des particules étudient des particules dont les vitesses sont proches de la vitesse de la lumière dans le vide.
- On parle alors de particules relativistes.
-
La mécanique classique est dans ce cas totalement
inadaptée pour l’étude des particules relativistes.
-
En physique des particules, la relativité restreinte fait
partie de l’expérience quotidienne.
-
Exemple :
-
Des particules instables, présentes dans les
accélérateurs de particules (CERN) peuvent être observées
pendant des durées très supérieures à leur durée de vie propre.
-
C’est une preuve expérimentale de la dilatation des
durées.
a)-
Les satellites de localisation GPS.
-
Le GPS (Global Position Système) comprend un ensemble de
24 satellites.
-
Chaque satellite embarque une horloge atomique de haute
précision et évolue sur une orbite circulaire autour de la
Terre.
-
Il émet régulièrement un signal électromagnétique
indiquant la date d’émission et sa position par rapport à la
Terre.
-
Le GPS situé dans une voiture (par exemple) détecte la
date d’arrivée du signal.
-
Avec ces deux informations, date d’arrivée et date
d’émission, le récepteur calcule la durée de propagation du
signal et en déduit la distance qui le sépare du satellite.
b)-
Principe de localisation.
-
Le principe de localisation
GPS repose sur la
localisation par triangulation.
-
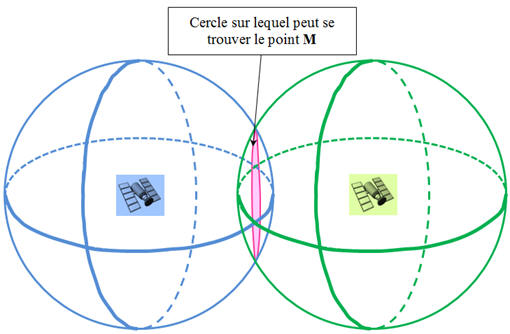
Pour localiser un point
M à la surface du globe
terrestre, il faut entrer en contact avec 4 satellites :
-
Avec le satellite
A, le point
M est
localisé sur une sphère de rayon R
égale à la distance
qui le sépare du satellite.
-
Avec deux satellites,
A et
B, le point
M
est localisé à l’intersection de deux sphères. Une telle
intersection est un cercle.
- Avec trois satellites, A, B et C, le point M est localisé à l’intersection de trois sphères.
- Une telle intersection donne deux positions possibles.
-
Le rôle du quatrième satellite permet de lever
l’ambiguïté restant entre les deux positions précédentes.
c)-
Gestion du temps.
-
Pour minimiser l’erreur sur les distances, toutes les
horloges doivent être parfaitement synchronisées.
-
Pour déterminer une distance à dix mètres près, quelle
doit être l’incertitude Δt sur la mesure de la durée du
trajet ?
-
On peut écrire :
-

-
Les horloges atomiques embarquées à bord de satellites
sont bien plus précises que cela.
-
En revanche, le récepteur
GPS d’une voiture ne peut
disposer d’une telle horloge chère et volumineuse.
-
Pour contourner cette difficulté, l’horloge électronique
du GPS d’une voiture est régulièrement remise à l’heure à l’aide
des signaux provenant des satellites.
d)-
La relativité et le
GPS.
- Les satellites GPS ne sont pas des satellites géostationnaires.
- Ils se déplacent à près de 20000 km d’altitude
avec une vitesse voisine de 3,9
x 103
m / s dans le référentiel géocentrique.
-
À cause de cette vitesse, leurs horloges retardent de 7
μs par jour par rapport aux horloges terrestres.
-
Ce retard relève de la théorie de la relativité
restreinte.
-
À cela s’ajoute un effet lié à la gravitation qui est lié
à la théorie de la relativité générale.
-
Cette théorie prévoit que deux horloges identiques
soumises à une gravité différente ne battent pas au même rythme.
-
À cause de ce deuxième phénomène, les horloges des
satellites GPS avancent de 45 μs par jour par rapport à une
horloge située au sol.
2)- Expérience de la lanterne sur le
mât d’un bateau.
4)- Exercices :
a)-
Exercice 9 page 219 : étudier un électron dans un tube
cathodique d’un téléviseur.
b)-
Exercice 11 page 220 : exploiter la relation entre durée
propre et durée mesurée.
c)-
Exercice 15 page 220 : une période variable.
d)-
Exercice 18 page 222 : Expérience de Bertozzi
e)-
Exercice 20 page 223 : Quand les durées se dilatent.
f)-
Exercice 26 page 225 : L’énergie relativiste.
|
|