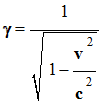1)- Expression de la valeur v de la vitesse de déplacement de l’électron dans ce référentiel terrestre.

-  Système étudié : l’électron

-  Référentiel terrestre (R)

-  Référentiel lié à l’électron (R’)

-  Schéma :

- 

2)- Valeur de v :

-  Valeur de la vitesse de déplacement d’un électron dans un référentiel terrestre.

-  Application numérique :

-   

1)- Durée du trajet de l’astronaute pour un observateur terrestre :

-  Schéma :

Cliquer sur l'image pour l'agrandir

-  Durée mesurée :

-  ΔT’ = γ . ΔT₀

-  L’astronaute se déplace à la vitesse v par rapport au référentiel terrestre.

-  Il parcourt la distance d = 4,0 a.l

-  1 a.l est la distance parcourue par la lumière en une année

-  1 a.l = c × a

-  Ainsi, la distance d peut être écrite en utilisant la formulation suivante :

-  d = 4,0 c × a

-  La durée du parcours est donnée par la relation :

-   

2)- Durée de ce même trajet pour l’astronaute :

-  Durée propre :

-  ΔT’ = γ . ΔT₀

-   

 On imagine qu’une fusée se déplace selon une trajectoire rectiligne avec une vitesse de valeur constante

 v = 250000 km . s^–1 par rapport à la Terre.

Données :

-  Les durées propre ΔT₀ et mesurée ΔT’ sont reliées par :

-  ΔT’ = γ . ΔT₀

-  Où

-  Avec v la valeur de la vitesse relative des horloges qui mesurent ΔT₀ et ΔT’

-  c = 3,0 × 10⁸ m . s ^–1

1)- Quels sont les deux évènements à considérer pour étudier la période du signal lumineux envoyé par l’astronaute à son ami ?

2)- Quelle est la période propre du signal lumineux ?

3)- Quelle est la période mesurée de ce signal par l’ami resté sur Terre ?

 1)- Les deux évènements à considérer pour étudier la période du signal lumineux envoyé par l’astronaute à son ami :

-  Évènement 1 : émission du signal à la date t₁

-  Évènement 2 : émission du signal à la date t₁ + T

-  T représente la période propre du signal dans la fusée.

Cliquer sur l'image pour l'agrandir

2)- Période propre du signal lumineux :

-   

3)- Période mesurée de ce signal par l’ami resté sur Terre :

-  Période mesurée :

-  ΔT’ = γ . ΔT₀

-   

1)- Analyse dimensionnelle et tableau :

a)-  Analyse dimensionnelle.

b)-  Tableau :

2)- Valeurs expérimentales et mécanique classique :

-  Tant que la vitesse des électrons est petite devant la vitesse de la lumière dans le vide,

les valeurs expérimentales sont en accord avec les résultats de la mécanique classique.

3)- Valeur limite de la vitesse que peuvent atteindre les électrons 

-  La valeur limite de la vitesse que peuvent atteindre les électrons est la vitesse de la lumière dans le vide

c = 3,0 × 10⁸ m . s ^–1

4)- Validité de la mécanique classique :

-  La mécanique classique n’est plus utilisable lorsque la valeur de la vitesse des particules est trop proche

de la valeur de la vitesse de la lumière dans le vide.

-  On peut utiliser la mécanique classique tant que v < 0,10 c.

La relativité restreinte conduit à des conclusions surprenantes dont celle de la dilatation des durées.

La lumière ayant une vitesse de valeur c indépendante du référentiel, la durée ΔT’ mesurée par O₂ sera supérieure à la durée ΔT₀.

1)- Lequel des observateurs mesure la durée propre ?

2)- Distance parcourue par la lumière par rapport à O₁ :

a)-  Pour O₁, quelle est la distance parcourue par la lumière lors d’un aller-retour entre les deux miroirs ?

b)-  Exprimer cette distance en fonction de c et ΔT₀.

3)- Distance parcourue par la lumière par rapport à O₂ :

a)-  Sur le schéma ci-dessous, on a représenté différentes positions de l’horloge observée par O₂

lors d’un aller-retour de la lumière entre les deux miroirs.

-  Schéma :

Cliquer sur l'image pour l'agrandir

-  Pour O₂, exprimer, en fonction de v et de ΔT’, la distance d parcourue par l’astronef pendant un aller simple de la lumière.

b)-  On appelle ℓ la distance parcourue par la lumière dans le référentiel lié à O₂ pendant la durée ΔT’.

Recopier et compléter le schéma de la question 3)- a)- en faisant apparaître d, L et .

c)-  Quelle est la relation entre d, L et ℓ ?

4)- Distances et durées :

a)-  Exprimer la distance ℓ en fonction de c et ΔT’.

b)-  À l’aide des questions précédentes, exprimer la durée ΔT’ en fonction de ΔT₀ et montrer que le coefficient γ apparaissant vaut :

-   

5)- Pourquoi parle-t-on de dilatation des durées dans le titre de l’exercice ?

1)- Observateur qui mesure la durée propre :

-  L’observateur O₁ étant immobile par rapport à son horloge, il mesure la durée propre ΔT₀.

-  Alors que l’observateur O₂ qui se déplace à la vitesse de valeur v par rapport à l’observateur O₁ donne la durée mesurée ΔT’.

2)- Distance parcourue par la lumière par rapport à O₁ :

a)-  Distance parcourue par la lumière lors d’un aller-retour entre les deux miroirs :

-  Schéma :

-  La lumière parcourt la distance D pour un aller-retour :

-  D = 2 L.

b)-  Expression cette distance en fonction de c et ΔT₀.

-  D = 2 L = c . ΔT₀

-   

3)- Distance parcourue par la lumière par rapport à O₂ :

a)-  Expression, en fonction de v et de ΔT’, de la distance d parcourue par l’astronef pendant un aller simple de la lumière.

-  L’astronef se déplace à la vitesse v pendant la durée ΔT’ et elle parcourt la distance 2 d.

-   

b)-  Schéma :

c)-  Relation entre d, L et ℓ :

-   

4)- Distances et durées :

a)-  Expression de la distance ℓ en fonction de c et ΔT’ :

-  La lumière se déplace à la vitesse c pendant la durée ΔT’ :

-  ℓ = c . ΔT’ 

b)-  Expression de la durée ΔT’ en fonction de ΔT₀ et expression du coefficient γ. 

-   

-  Avec

-  ΔT’ = γ . ΔT₀

5)- La dilatation des durées.

-  Comme :

-   

-  La durée ΔT’ > ΔT₀

-  Par rapport à l’observateur O₂, l’horloge de l’astronef semble ralentir, elle retarde.

-  Les durées sont plus longues pour l’observateur O₂ par rapport à l’observateur O₁.

 Dans le vide, l’énergie relativiste totale E d’une particule de masse m s’exprime par :

-  E² = p² . c²+ m² . c⁴

-  p est la valeur de la quantité de mouvement relativiste.

-  avec

-  Et  la vitesse de la particule dans le référentiel terrestre.

1)- Montrer que cette énergie peut se mettre sous la forme :

-  E = γ . m . c²

2)- L’énergie relativiste totale E de la particule est la somme de son énergie cinétique relativiste E_c

(qui dépend de la valeur de la vitesse v de la particule dans le référentiel galiléen) et de son énergie de masse,

appelée aussi énergie au repos, E₀ = m . c², indépendante de v.

-  Déterminer l’expression relativiste de l’énergie cinétique d’une particule de masse m.

3)- Contrairement à la mécanique classique, la théorie de la relativité restreinte prévoit qu’une particule de masse nulle, par exemple un photon, transporte de l’énergie.

a)-  Que dire du rapport  dans le cas d’une particule de masse nulle ?

b)-  Que peut-on en déduire à propos du coefficient γ d’une telle particule ?

c)-  En déduire la valeur de la vitesse dans le vide d’une particule de masse nulle.

4)- Un photon transporte une énergie E qui dépend de la fréquence υ de la radiation associée.

a)-  Pour un photon, exprimer E en fonction de la fréquence υ, puis de la longueur d’onde λ de cette radiation.

b)-  Pour un photon, exprimer E en fonction de p et c.

c)-  En déduire, pour un photon, l’expression de p en fonction de λ.

1)- Expression de l’énergie totale E.

-  E² = p² . c²+ m² . c⁴

-  E² = (γ . m . v)². c² + m² . c⁴

-   

-  E = γ . m . c²

2)- Expression relativiste de l’énergie cinétique d’une particule de masse m.

-  E = γ . m . c² et E = E_c + E₀ avec E₀ = m . c²

-   

3)- Le photon :

a)-  Étude du rapport  :

-   

-  Si m = 0, alors

b)-  Coefficient γ pour le photon.

-  Comme la masse d’un photon est nulle et que son énergie a une valeur finie,

-  Or, comme le rapport

-  On tire que le coefficient γ → + ∞

c)-  Valeur de la vitesse dans le vide du photon

-  Dans le cas d’un photon, le coefficient γ → + ∞

-  Avec

-  En conséquence

- 

-  La vitesse de déplacement des photons est  :

-  la vitesse de la lumière dans le vide.

4)- Photon et énergie :

a)-  Expression de E en fonction de la fréquence υ, puis de la longueur d’onde λ de cette radiation.

-  Énergie d’un photon :

-  Chap. N° 03 Sources de lumières colorées (1S)

-  E = h . ν ou

-  Pour une onde électromagnétique de fréquence ν et de longueur d’onde λ dans le vide

-  La grandeur h est la constante de Planck : h = 6,62 × 10 ^{– 34} J.s.

-  La grandeur c représente la valeur

-  de la vitesse de la lumière dans le vide :

-  c = 3,00 × 10 ⁸ m / s

-  L’énergie E s’exprime en joule.

b)-  Expression de E en fonction de p et c

-  E² = p² c² + m² . c⁴

-  Pour un photon, m = 0

-  E = p . c

c)-  Expression de p en fonction de λ

-   

1)- Le problème des jumeaux.

a)-  À quel phénomène fait référence la phrase surlignée ?

b)-  Expliquer l’indication : « mais non de son propre point de vue ».

c)-  Expliquer, en utilisant la notion de référentiel, la signification de la phrase : « Mais on peut raisonner dans l’autre sens ».

d)-  Quelle propriété doit vérifier un référentiel pour que l’on puisse lui appliquer les lois de la relativité restreinte ?

e)-  On peut admettre que le référentiel géocentrique vérifie cette propriété.

Montrer que cela ne peut pas être le cas pour le référentiel du vaisseau.

En conclure que les situations des jumeaux ne sont pas symétriques.

f)-  La réciprocité des situations ne s’applique donc pas aux « jumeaux » : Quelle en est la conséquence ?

2)- Le principe de causalité.

a)-  En utilisant le principe de causalité décrit dans la dernière phrase du texte, répondre à la question suivante :

si un terrien calcule que la chute d’une météorite sur Jupiter provenant du système solaire s’est produite avant

l’explosion d’une supernova, est-il envisageable qu’il existe un référentiel dans lequel l’explosion s’est produite avant la chute de la météorite ?

b)-  De même, si une bouffée de particules due à une éruption solaire arrive sur la Terre,

existe-t-il un référentiel dans lequel l’arrivée des particules sur la Terre se produit avant l’éruption ?

1)- Le problème des jumeaux.

a)-  Phénomène mis en évidence :

-  Pendant son voyage, tout semble ralentir (ses horloges, son cœur) du point de vue de son frère resté sur Terre

-  C’est le phénomène de dilatation des durées pour un objet en mouvement

-  ΔT’ = γ . ΔT₀ avec γ ≥ 1

-  La durée mesurée est supérieure à la durée propre.

-  Une horloge qui se déplace par rapport à un observateur bat plus lentement qu’une horloge immobile par rapport à l’observateur.

b)-  Explication de l’indication : « mais non de son propre point de vue ».

-  La dilatation des durées concerne la mesure des durées dans deux référentiels se déplaçant l’un par rapport à l’autre.

-  Une durée propre concernant un objet est une durée mesurée par une horloge immobile dans le référentiel propre à cet objet.

-  Dans le référentiel propre au voyageur, celui-ci ne voit pas de changement dans l’écoulement du temps.

-  Il perçoit le changement de l’écoulement du temps dans le référentiel lié dans l’autre référentiel qui se déplace par rapport à lui.

c)-  Signification de la phrase et notion de référentiel :

-  « Mais on peut raisonner dans l’autre sens ».

-  On peut raisonner du point de vue du voyageur, en choisissant son référentiel comme étant immobile et

le référentiel terrestre en mouvement.

d)-  Propriété du référentiel pour que l’on puisse lui appliquer les lois de la relativité restreinte :

-  Pour pouvoir appliquer les lois de la relativité restreinte, le référentiel doit être galiléen.

e)-  Situations des jumeaux.

-  Le référentiel lié au vaisseau n’est pas galiléen :

-  Le référentiel lié au vaisseau doit accélérer au départ, puis ralentir à l’arrivée.

-  Il doit opérer un demi-tour pour revenir.

-  Le mouvement du référentiel lié au vaisseau n’est pas rectiligne uniforme.

-  Ce n’est pas un référentiel galiléen.

-  Alors que le référentiel terrestre lié à l’autre jumeau est galiléen.

-  Les situations des deux jumeaux ne sont pas symétriques :

-  Le jumeau situé dans le vaisseau subit une accélération et un ralentissement alors que celui resté sur Terre

se déplace d’un mouvement rectiligne uniforme.

f)-  Conséquence de la non-réciprocité des situations des « jumeaux » :

-  Il n’y a pas de réciprocité dans les situations des deux jumeaux.

-  Il découle de ceci qu’il n’est pas contradictoire de ne pas retrouver les deux jumeaux au même stade de vieillissement.

-  C’est l’application incorrecte de la réciprocité de la situation qui conduit à ce que l’on appelle le paradoxe des jumeaux de Langevin.

2)- Le principe de causalité.

a)-  Cas d’évènements indépendants :

-  Les évènements étant indépendants, le cas est envisageable.

-  Il peut exister un référentiel dans lequel l’explosion s’est produite avant la chute de la météorite.

b)-  Cas d’évènements dépendants :

-  L’arrivée des particules sur Terre avant l’éruption :

-  Cette situation est impossible car c’est l’éruption qui produit les particules.

-  L’éruption est la cause de l’arrivée des particules.

-  Les deux évènements sont liés.