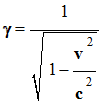|
QCM N° 08 |
Temps et relativité restreinte. |
|
|
|
Temps et relativité restreinte :
Pour chaque question, indiquer la (ou les) bonne(s) réponse(s).
Donnée :
|
|||||
|
|
Énoncé |
A |
B |
C |
R |
|
1 |
En relativité restreinte, la valeur
de la vitesse de la lumière dans
le vide et dans un référentiel galiléen : |
Est absolue. |
Est relative. |
Dépend du
référentiel. |
A |
|
2 |
L’invariance dans le vide de la valeur
de la lumière dans un référentiel
galiléen est un postulat de : |
Galilée. |
Newton. |
Einstein. |
C |
|
3 |
En relativité restreinte, l’horloge
qui mesure le temps propre séparant
deux évènements doit être : |
Éloignée des
lieux des
évènements. |
Proche des
lieux des
évènements. |
En mouvement
par rapport
au lieu où
se déroulent
ces deux
évènements. |
B |
|
4 |
En relativité restreinte, les durées
mesurées sont : |
Contractées
par rapport
aux durées
propres. |
Les mêmes
que les
durées propres. |
Dilatées
par rapport
aux durées
propres. |
C |
|
5 |
Les durées mesurée ΔT’ et
propre ΔT0 sont reliées par la
relation ΔT’ = γ . ΔT0. |
γ
s’exprime
en m . s–1. |
γ
s’exprime
en s–1. |
γ
est
sans unité |
C |
|
6 |
Deux personnes munies de
chronomètres, fixes dans deux
référentiels galiléens, observent
les deux mêmes évènements.
Les durées séparant ces deux
évènements sont sensiblement
différentes si : |
Ces deux
personnes sont
en mouvement
l’une par
rapport à
l’autre à une
vitesse de
valeur élevée. |
Ces deux
personnes sont
en mouvement
l’une par
rapport à
l’autre à une
vitesse de
faible valeur. |
Ces deux
personnes ne
sont pas en
mouvement
l’une par
rapport à
l’autre. |
A |
|
7 |
On imagine qu’une personne A
munie d’un chronomètre se
déplace à 225 000 km . s–1 par
rapport à une personne B.
La personne B est également
munie d’un chronomètre et les
référentiels liés à A et B sont
galiléens.A
mesure la durée
propre séparant deux évènements.
c
= 3,00
×
108 m . s–1 |
La durée
mesurée par
la personne B
entre les deux
évènements
est environ
2 fois plus
grande que
celle mesurée
par la
personne A. |
La durée
mesurée par
la personne B
entre les deux
évènements est
environ 1,5
fois plus
grande que
celle mesurée
par la
personne A. |
La durée
mesurée par
la personne B
entre les
deux évènements
est sensiblement
égale à celle
mesurée par
la personne A. |
B |
|
8 |
La mécanique classique : |
Est un
cas particulier
de la
mécanique
relativiste. |
Est une
généralisation
de la
mécanique
relativiste. |
Correspond
au cas où γ = 1. |
AC |
|
9 |
Le caractère relatif du temps
est-il à prendre en compte par
un observateur fixe dans un
référentiel terrestre lorsqu’il
mesure la période de battement
des ailes d’une mouche volant
à 10 km . h–1 ? |
Oui. |
Non. |
On ne
peut pas
savoir sans
connaître la
période propre
des battements. |
B |
|
10 |
Une fusée se dirige avec une vitesse v
vers une source lumineuse immobile
dans un référentiel galiléen. Par
rapport au référentiel de la fusée,
la vitesse de propagation de la lumière
dans le vide est : |
Supérieure
à c. |
Égale
à c. |
Inférieure
à c. |
B |
|
11 |
D’après les postulats de la relativité
restreinte, si on décrit le mouvement
d’un électron soumis à un champ
électromagnétique dans deux
référentiels galiléens différents : |
Les trajectoires
sont décrites
de façons
identiques. |
Les vitesses
sont, à
chaque instant,
identiques. |
Les mêmes
lois de
l’électromagnétisme
sont respectées. |
C |
|
12 |
Une fusée se dirige avec une vitesse
v
vers une station spatiale immobile
dans un référentiel galiléen. Pour un
occupant de la station, par
comparaison avec une horloge de la
station, une horloge embarquée
dans la fusée : |
Prend
de l’avance. |
Prend
du retard. |
Indique
le même
temps. |
B |
|
13 |
Les muons sont des particules
instables qui se désintègrent en
moyenne au bout d’une durée propre τ.
Dans un laboratoire, la durée
d’existence mesurée pour des muons
animés d’une vitesse proche de c est
en moyenne : |
Grande
devant τ. |
Égale
à τ. |
Petite
devant τ. |
A |
|
14 |
Une durée mesurée d’un phénomène
est toujours : |
Supérieure
ou égale
à sa durée
propre. |
Inférieure
ou égale à
sa durée
propre. |
Égale à
sa durée
propre. |
A |
|
15 |
Concernant les véhicules construits
et utilisés par l’homme, la relativité
du temps : |
N’est pas
vérifiable. |
Est vérifiable
mais n’a
aucune
conséquence
pratique. |
Est vérifiable
est peut
avoir des
conséquences
pratiques. |
C |
►Postulats
2 :
-
La vitesse de propagation de la lumière dans le
vide est indépendante du mouvement de la source lumineuse et
elle est invariante dans tout changement de référentiel
galiléen.
-
Un évènement est un phénomène objectif observable,
c’est un fait se produisant à un endroit donné.
-
Cas : Référentiel galiléen (R’) en
mouvement par rapport au référentiel galiléen (R).
-
La durée propre ΔT0 :
-
La durée propre ΔT0, est la
durée séparant deux évènements mesurée par une horloge fixe
ayant lieu au même point dans un référentiel galiléen (R).
-
Cette durée ΔT0 est mesurée par
une horloge fixe, proche des deux évènements dans le référentiel
(R).
-
On utilise les termes de « temps propre » ou
« durée propre » (on préfère le terme « durée propre »).
-
Une durée propre concernant un objet est une durée
mesurée par une horloge immobile dans le référentiel propre à
cet objet.
-
La durée mesurée ΔT’ :
-
La durée mesurée ΔT’ est la durée séparant
deux évènements mesurée par une horloge fixe ayant lieu au même
point dans un référentiel galiléen (R’) en mouvement par
rapport au référentiel galiléen (R).
-
Dans le référentiel (R), on mesure la
durée propre.
-
Dans le référentiel (R’), on mesure la
durée mesurée.
-
Le référentiel (R’) est en mouvement par
rapport au référentiel (R).
-
Relativité du temps :
-
Les durées ΔT’ et ΔT0
sont liées par la relation de dilatation temporelle :
-
ΔT’ = γ . ΔT0
-
Le coefficient γ (gamma), sans unité, est
donné par la relation :
|
|
|
-
Dilatation des durées :
-
Deux horloges en mouvement relatif ne mesurent pas
la même durée entre deux évènements
-
ΔT’ ≥ ΔT0
-
C’est le phénomène de dilatation des durées.
-
Une horloge qui se déplace par rapport à un
observateur bat plus lentement qu’une horloge immobile par
rapport à l’observateur.
-
Expression de γ :
|
|
|
-
Lorsque la vitesse v << c, la dilatation de
temps est imperceptible.
-
Si v << c, alors γ ≈ 1 et
ΔT’ ≈ ΔT0
-
Si v ≈ c, alors γ > 1 et
ΔT’ > ΔT0
-
Valeur de γ :
-
c = 3,00
x 108 m . s–1 et v ≈ 2,25
x 108 m . s–1
-
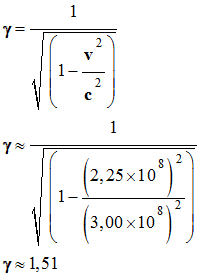
-
Lorsque la vitesse v << c, la dilatation de
temps est imperceptible.
-
Le postulat d’Einstein est compatible avec les
lois de la mécanique classique de Galilée et Newton.
-
Si v << c, alors γ ≈ 1 et
ΔT’ ≈ ΔT0
-
Dans ce cas, la mesure de la durée est
indépendante du référentiel choisi.
►Postulat
d’Einstein :
-
La vitesse de propagation de la lumière dans le
vide est indépendante du mouvement de la source lumineuse et
elle est invariante dans tout changement de référentiel
galiléen.
►Postulat
1 :
-
Les lois de la physique s’expriment de la même
façon dans tous les référentiels galiléens.
►Postulat
2 :
-
La vitesse de propagation de la lumière dans le
vide est indépendante du mouvement de la source lumineuse et
elle est invariante dans tout changement de référentiel
galiléen.
-
Lois physiques :
- Les lois de la physique sont les mêmes dans tous les référentiels galiléens.
- Ceci ne signifie pas que les
mouvements sont décrits de façons identiques.
►Durée
propre et durée mesurée :
-
Dans le référentiel (R) lié à la station
spatiale, on mesure la durée propre.
-
Dans le référentiel (R’) lié à la fusée, on
mesure la durée mesurée.
-
Le référentiel (R’) est en mouvement par
rapport au référentiel (R).
-
Relativité du temps :
-
Les durées ΔT’ et ΔT0
sont liées par la relation de dilatation temporelle :
-
ΔT’ = γ . ΔT0
-
Deux horloges en mouvement relatif ne mesurent pas
la même durée entre deux évènements
-
ΔT’ ≥ ΔT0
-
C’est le phénomène de dilatation des durées.
-
L’horloge située dans la fusée retarde par rapport
à l’horloge située dans la station spatiale.
- Dans un laboratoire, la durée d’existence mesurée pour des muons animés d’une vitesse proche de c est en moyenne grande devant τ.
- Il y a en effet dilatation des
durées pour la particule en mouvement par rapport au
laboratoire.
►Durée
propre et durée mesurée :
-
Deux horloges en mouvement relatif ne mesurent pas
la même durée entre deux évènements
-
ΔT’ ≥ ΔT0
-
C’est le phénomène de dilatation des durées.
-
Une horloge qui se déplace par rapport à un
observateur bat plus lentement qu’une horloge immobile par
rapport à l’observateur.
►Relativité
du temps :
- La relativité du temps est vérifiable et peut avoir des conséquences pratiques.
- C’est un effet faible mais mesurable avec des horloges atomiques.
- Le GPS est un
exemple où les effets relativistes ont des conséquences
pratiques.
- Les satellites GPS ne sont pas des satellites géostationnaires.
- Ils se déplacent à près de 20000 km d’altitude
avec une vitesse voisine de 3,9
× 103
m / s dans le référentiel géocentrique.
-
À cause de cette vitesse, leurs horloges retardent
de 7 μs par jour par rapport aux horloges terrestres.
-
Ce retard relève de la théorie de la relativité
restreinte.
|
|