QCM réalisé avec le logiciel QUESTY

Pour s’auto-évaluer

AIDE

Stabilité d’un noyau :

-     Un noyau est instable s’il possède trop de protons par rapport au nombre de neutrons.

-     Un noyau est instable s’il possède trop de neutrons par rapport au nombre de protons.

-     Un noyau est instable s’il possède trop de protons et trop de neutrons (trop de nucléons).

-     Ils se désintègrent spontanément, on dit qu’ils sont radioactifs.

-     Ce sont des radionucléides.

Radioactivité α, β⁺ et β^–.

-     Une source radioactive peut émettre :

-     Des particules

-     Un rayonnement γ.

-     Les particules émises sont de trois types : les particules α, β⁺et β^–.

►    Les particules α (alpha).

-     Ce sont des particules positives, des noyaux d’hélium dont l’écriture symbolique :

-    , ion He²⁺.

►    Les particules β (bêta).

-     On distingue :

-     Les particules β^– (bêta moins) qui sont des électrons :

-     Symbole :

-     Les particules β⁺ (bêta plus) qui sont des positons (antiparticule de l’électron).

-     Symbole :

►    Le rayonnement γ (gamma).

-     Il accompagne l’émission de particules α, β⁺et β^–.

-     Il est constitué d’une onde électromagnétique de très courte longueur d’onde

-     (λ ≈ 10^–12 m et υ ≈ 10 ²⁰ Hz).

Désintégration radioactive :

-     Au cours d’une désintégration radioactive, un noyau instable se transforme spontanément en un noyau d’un autre élément chimique.

-     Cette désintégration s’accompagne de l’émission d’une particule et d’un rayonnement gamma.

-     Le noyau qui se désintègre est appelé :

-     le noyau-père:

-     et le noyau formé est appelé :

-     Le noyau-fils,

-     Il existe trois types de radioactivité, caractérisés par la particule émise lors de la désintégration du noyau radioactif :

-     Tableau :

-     Une particule, α, β⁺ou β^–,

Équation de réaction de désintégration nucléaire.

-     Une réaction de désintégration radioactive est modélisée par une équation.

-     Cette équation vérifie les lois de conservation suivantes :

-     Conservation du nombre de charge Z.

-     Conservation du nombre de masse A.

Les trois types de radioactivité :

Radioactivité α :

-     Un noyau lourd instable éjecte une particule α et donne un noyau-fils plus léger, généralement dans un état excité.

-     L’uranium 238 est émetteur a.

-     Écrire l’équation de la réaction.

Diagramme (N, Z) :

-     Dans ce diagramme, on porte :

-     En abscisse, le nombre N de neutrons du noyau

-     En ordonnée, le nombre de protons du noyau.

-     Chaque isotope y est  représenté par une case.

-     On retrouve sur une même ligne les isotopes d’un même élément.

Loi de décroissance radioactive :

-     Un noyau instable est susceptible de revenir à l’état stable à tout moment.

-     Le phénomène de désintégration est imprévisible.

-     Pour un noyau instable donné, on ne peut prévoir la date de sa désintégration.

-     En revanche, on connaît la probabilité de désintégration de ce noyau par unité de temps.

-     Le phénomène de désintégration est aléatoire.

-     L’évolution, au cours du temps, du nombre N (t) de noyaux radioactifs d’un échantillon peut être modélisée par la loi de décroissance radioactive :

-     λ est la constante de désintégration (ou de décroissance) radioactive s ^–1.

La constante radioactive λ.

-     Chaque nucléide radioactif est caractérisé par une constante de désintégration radioactive λ, qui est la probabilité de désintégration d’un noyau par unité de temps.

-     Elle s’exprime en s^–1.

Demi-vie t_1/2.

-     Définition :

-     Pour un type de noyaux radioactifs, la demi-vie t_1/2 est la durée au bout de laquelle la moitié des noyaux radioactifs initialement présent dans l’échantillon se sont désintégrés.

-     Relation entre t_1/2 et λ :

-     

-     La demi-vie n’a qu’une valeur statistique.

-     Elle indique qu’un noyau radioactif a une chance sur deux de disparaître au bout d’une demi-vie.

►    Courbe de décroissance : N = f (t).

-     On peut déterminer la demi-vie d’un noyau radioactif à partir de la courbe de décroissance radioactive.

-     Représentation graphique :

-     La demi-vie du carbone 14 est d’environ 5700 ans.

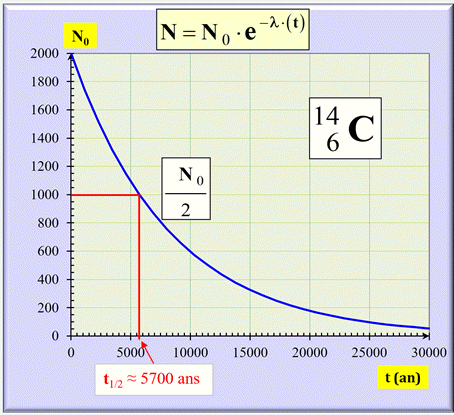
Activité d’un échantillon.

-     L’activité A (t) d’un échantillon radioactif à la date t est le nombre de désintégrations par seconde de cet échantillon.

-     L’unité d’activité est le Becquerel Bq en hommage à Henri Becquerel.

-     1 Bq = 1 désintégration par seconde.

-     L’activité, à un instant donné, est égale à l'opposé de la dérivée par rapport au temps de N (t).

-      

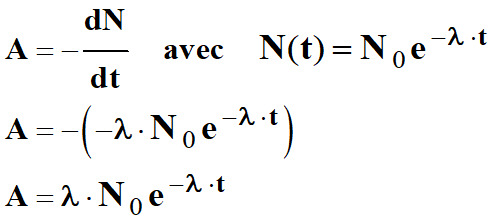
- L'hydrogène 3 est émetteur β⁻

-     La décroissance de l’activité suit la même loi que la décroissance du nombre de noyau radioactif d’un échantillon.

►    Courbe de décroissance : A = f (t) pour le carbone 14

-     Ordre de grandeur des activités : l’eau de mer a une activité de l’ordre de 10 Bq par litre.

-     Le Radon, présent dans l’air, à l’état de trace, a une activité de quelques centaines de Bq.

-     Le corps humain A ≈ 10 ⁴ Bq,

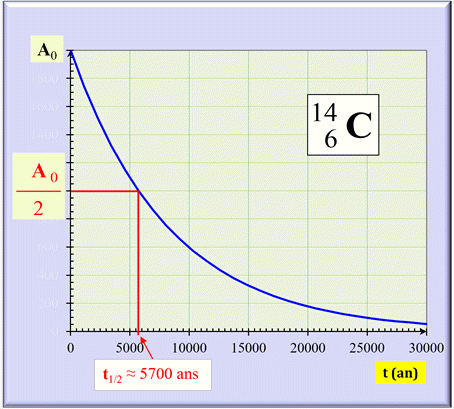
Datation d’un objet.

►    La datation au carbone 14.

-     Elle est fondée sur l’utilisation de la loi de décroissance radioactive de l’isotope , radioactif β^–.

-     La demi-vie du carbone 14 est fixée de façon conventionnelle à t _½ = 5734 ± 40 ans (valeur admise en 1961).