|
Mécanique des fluides |
|
|
|
|
|
|
QCM N° 14
Mécanique des
fluides.
Pour chaque
question, indiquer la (ou les) bonne(s) réponse(s). |
|||||
|
|
Énoncé |
A |
B |
C |
R |
|
1 |
La relation
entre
masse
volumique ρ,
volume V
et masse m
d’un corps
solide
homogène peut
s’écrire : |
|
|
|
B |
|
2 |
La masse
volumique
d’un liquide
est : |
Du même
ordre de
grandeur que
celle d’un gaz |
Très
supérieure
à celle
d’un gaz |
Très
inférieure
à celle
d’un gaz |
B |
|
3 |
La relation
entre la
norme F de la force
pressante, la
pression
P
et la surface S est : |
|
|
|
B |
|
4 |
La norme de la
force
pressante
exercée par
un gaz à la
pression
P
= 800 hPa sur une
paroi de
surface
S
= 10 m2 vaut : |
8,0 × 102
N |
8,0 × 10–4
N |
8,0 × 105
N |
C |
|
5 |
Dans un
liquide, la
différence de
pressions
PA
– PB entre deux
points A
et B : |
Est
proportionnelle
à la
différence
de leurs
altitudes
zB
– zA |
Est
proportionnelle
à la masse
volumique
du liquide |
Est
toujours
positive |
AB |
|
6 |
La masse
volumique de
l’eau salée
est supérieure
à celle de
l’eau douce.
La pression à
100 m
de
profondeur : |
Est supérieure
dans un
lac que
dans la mer |
Est identique
dans un lac et
dans la mer |
Est plus
faible
dans un
lac que
dans la mer |
C |
|
7 |
Dans l’eau, la
pression
vaut 4,5 bar à
une
profondeur
de : Données : masse volumique de l’eau
douce :
ρeau
= 1,0 × 103 kg . m–3
norme du champ
de pesanteur :
g
= 10 N . kg–1
pression
atmosphérique : Patm = 1,0 ×105 Pa
Patm
= 1,0 bar |
45 m |
35 m |
0,45 m |
B |
|
8 |
Lorsque la
vitesse d’un système est
doublée : |
Son énergie
cinétique
est doublée |
Son énergie
est divisée
par 2 |
Son énergie
cinétique
est
quadruplée |
C |
|
9 |
La vitesse
v d’un
système de
masse m
et d’énergie
cinétique
EC
vaut : |
|
|
|
A |
|
10 |
L’énergie
cinétique
d’une voiture
d’une tonne ayant une vitesse de 50 km . h–1
est : |
De l’ordre
de 105
J |
De l’ordre
de 102
J |
De l’ordre
de 106
J |
A |
|
11 |
La variation
de l’énergie
potentielle de
pesanteur d’un système de masse m passant d’une
l’altitude
zA
à une altitude
zB est : |
m
. g . (zA – zB) |
m
. g . (zB – zA) |
m
. g . (zA – zB)
si zA > zB
m
. g . (zB – zA)
si zB > zA |
B |
|
12 |
Un corps est en
équilibre
mécanique si :
|
La somme
des vecteurs
forces qui
s’exercent sur
lui est égale
au vecteur nul |
La somme
des normes
des forces
qui s’exercent
sur lui
est nulle |
Son poids
est nul |
A |
|
13 |
L’énergie
mécanique d’un objet de masse
m,
d’altitude z et de
vitesse v
est : |
|
|
|
A |
|
14 |
L’énergie
mécanique
d’un solide en
chute
libre dans le
vide : |
Diminue car
son altitude
diminue |
Augmente car
sa vitesse
augmente |
Est constante
car seul
le poids
s’applique
sur l’objet |
C |
QCM réalisé avec le logiciel Questy
Pour s’auto-évaluer
La masse volumique :
-
C’est la masse par unité de
volume.
|
|
m
:
Masse de l’espèce ou du mélange en kg
V
:
Volume l’espèce ou du mélange en m3
ρ : Masse volumique de l’espèce ou du mélange en kg . m–3 |
-
à ne pas confondre avec la
concentration en masse ou titre massique :
|
|
t
: concentration en masse en
soluté en g / L
msoluté
:
masse de soluté en g.
Vsolution
:
volume de la solution en L. |
Masse volumique et état de la matière :
-
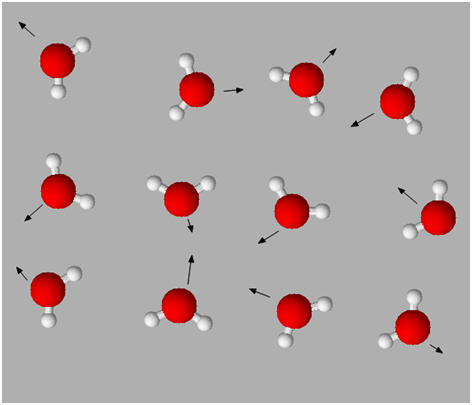
L’état gazeux est un
état dispersé alors que l’état liquide est un état condensé.
-
Les molécules et les
ions sont éloignés les uns des autres et se déplacent dans toutes les directions
de façon désordonnée.
-
Les interactions entre
les entités chimiques sont faibles.
-
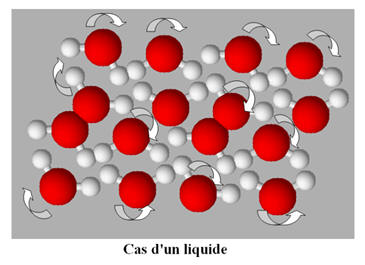
L’état liquide comme
l’état solide est un état condensé.
-
À l’état liquide,
les entités chimiques sont les unes contre les autres et peuvent glisser les
unes sur les autres.
-
Les entités chimiques
sont en mouvement constant.
-
La masse volumique
d’un liquide est très supérieure à celle d’un gaz.
Chap. N° 11 Description d'un fluide au
repos cours (classe de première)
Force pressante et pression :
-
La force pressante
résulte des chocs entre les entités, qui constituent le fluide, et les parois du
récipient.
-
Un fluide exerce une
force pressante sur les parois du récipient qui le contient .
-
La
valeur F
de la pression dépend de la pression
P
du fluide et de la surface de contact
S
|
|
|
|
|
Point
d’application :
on choisit le
centre de la
surface pressée |
|
Direction :
perpendiculaire à la paroi |
|
|
Sens :
orienté du fluide vers la paroi |
|
|
Valeur :
F
en newton (N) |
|
-
Relation :
|
F
= P . S
ou
ou
|
P :
Pression en N . m–2 ou pascal (Pa) |
|
S :
Surface de contact en m2 |
|
|
F ;
force pressante en newton (N) |
Norme (valeur) de la force pressante
-
1 hPa = 100 Pa (h :
hecto)
-
F
= P .
S = 800 × 100 × 10
-
F
≈ 8,0 × 105
N
Pression et différence de pression dans un liquide
immobile :
-
Pression dans l’eau et
profondeur.
-
Loi fondamentale de la
statique des fluides :
|
PB
– PA
= ρ . g . ( zA
– zB)
|
|
P :
Pression en pascal (Pa) |
|
ρ
: masse volumique du fluide au repos (kg . m–3) |
|
g :
intensité de la pesanteur (N . kg–1) |
|
z :
coordonnée verticale (m) L’axe des
coordonnées verticales est orienté vers le haut |
-
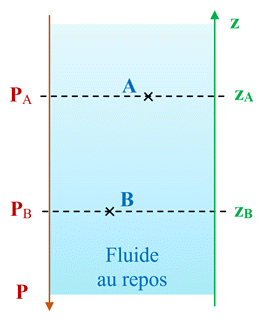
Schéma :
-
Deux
points A
et B,
situés dans un même liquide au repos, de mêmes coordonnées verticales (zA = zB)
sont à la même pression (PA = PB).
-
Deux
points A
et B,
situés dans un même liquide au repos, de coordonnées verticales différentes (zA ≠ zB)
sont à des pressions différentes (PA ≠ PB).
-
Attention aux indices
A et
B.
Pression et masse volumique d’un liquide :
-
Relation :
-
Pression au point
A à 100 m de
profondeur:
-
PA
= ρ .
g . (
zA)
-
La pression dans un
liquide est proportionnelle à la masse volumique du liquide.
-
Comme
ρlac
< ρmer,
alors à 100 m, Plac
<Pmer.
Pression et profondeur :
-
La pression dépend de
la profondeur.
-
Autre
donnée : Patm = 1,0 ×105
Pa = 1,0 bar
-
Schéma de la
situation :

-
PB
– PA
= ρ .
g . (
zA
– zB)
-
PB
– PA
= – ρ
. g .
zB
- 
-
La pression est de 4,5
bar à une profondeur de 35 m.
Chap. N° 14 Aspects énergétiques des
phénomènes mécaniques (classe de première)
Énergie cinétique d’un système :
-
L’énergie cinétique
est l’énergie que possède un solide du fait de son mouvement.
-
Elle dépend de la
vitesse et de la masse du solide.
-
Pour un solide animé
d’un mouvement de translation, tous les points du solide ont à chaque instant la
même vitesse que le centre d’inertie du solide :
-
L’énergie cinétique EC
d’un système en mouvement de translation est égale au demi-produit de la masse
m
du solide par le carré de la vitesse
v2
du système.
-
On écrit :
|
Relation |
Unités |
|
|
EC
en joule (J) |
|
m
en kilogramme (kg) |
|
|
v
en mètre par seconde m . s–1 |
-
L’énergie cinétique
caractérise un système en mouvement.
-
Elle est
-
Proportionnelle à la masse m du solide
-
Proportionnelle au carré de la vitesse
v
du système.
-
Elle dépend du
référentiel d’étude.
-
Si la vitesse du
système est doublée, son énergie cinétique est multipliée par 4.
Énergie cinétique d’un système et vitesse v du système :
-

Calcul de l’énergie cinétique d’un système :
-

-
Ordre de grandeur :
Ec
≈ 105 J
Énergie potentielle de pesanteur :
|
EPP =
m . g . z |
EPP :
énergie potentielle de pesanteur joule (J) |
|
m :
masse de l’objet en kilogramme (kg). |
|
|
g :
facteur
d’attraction terrestre : g = 9,81 N / kg ou g =
9,81 m / s². |
|
|
z :
altitude du centre d’inertie de l’objet en mètre (m). |
-
La valeur de l’énergie
potentielle de pesanteur dépend de la valeur de
z, elle dépend du
choix de l’origine des altitudes.
-
L’énergie potentielle
est définie à une constante additive près.
-
Altitude de départ :
zA
-
Altitude d’arrivée :
zB
-
Variation de l’énergie
potentielle de pesanteur :
-
ΔEPP =
EPPB –
EPPA
-
La différence
d’énergie potentielle ne dépend pas du choix de l’origine.
-
ΔEPP =
EPPB –
EPPA=
m .
g . zB
– m .
g . zA
-
ΔEPP =
m .
g . (zB
– zA)
Chap N° 11 Principe d’Inertie (classe de
seconde)
Équilibre d’un solide :
-
Principe d’Inertie.
-
Deux forces se
compensent si elles ont
-
La même droite
d’action
-
Des sens opposés,
-
Et la même valeur.
-
La somme vectorielle
des représentants de ces forces est égale au vecteur nul :
-
![]()
-
Énoncé : Principe
d’Inertie :
|
Lorsque les
forces qui s’exercent sur un système se compensent
alors le vecteur vitesse
|
-
Autre formulation :
|
Lorsque les
forces qui s’exercent sur un système se compensent, alors le
système reste immobile, ou reste en mouvement rectiligne uniforme. C’est-à-dire : |
-
Réciproque du principe
d’Inertie :
|
Si le vecteur
vitesse
alors le système est soumis à de forces qui se compensent.
|
-
Principe de
l’Inertie :
-
Lorsque les forces qui
s’exercent sur un système se compensent, alors le système reste immobile, ou
reste en mouvement rectiligne uniforme.
-
S’il est immobile on
dit aussi qu’il est en équilibre :
-
Un corps en équilibre
est soumis à des forces qui se compensent.
-
La somme vectorielle
des forces appliquées au système est égale au vecteur nul.
-
![]()
Énergie mécanique :
-
L’énergie mécanique Em
d’un système S
de masse m
est égale à la somme de son énergie cinétique
EC
et de son énergie potentielle
EP.
-
Em
= EC
+ EP
-
L’énergie mécanique Em
d’un système S
de masse m
dépend de la valeur de la vitesse
v
du système et de sa position dans le référentiel d’étude.
-
Énergie cinétique :
|
Relation |
Unités |
|
|
EC
en joule (J) |
|
m
en kilogramme (kg) |
|
|
v
en mètre par seconde m . s–1 |
-
Énergie potentielle de
pesanteur :
|
EPP = m
. g . z |
EPP : énergie potentielle en joule
(J) |
|
m
: masse du système en kilogramme (kg) |
|
|
z
: altitude du système en mètre (m) |
|
|
g
facteur d’attraction terrestre :
g
= 9,81 N . kg–1 ou
g
= |
-

Énergie mécanique et chute libre d’un système :
-
Un objet en chute
libre n’est soumis qu’à son poids.
-
Le
poids
![]() , étant est une force conservative, on lui associe une énergie potentielle
de pesanteur EPP.
, étant est une force conservative, on lui associe une énergie potentielle
de pesanteur EPP.
-
Lors de la chute
libre, l’altitude du système diminue, en conséquence, son énergie potentielle
diminue.
-
Simultanément, sa
vitesse augmente et de ce fait, son énergie cinétique augmente.
-
Au cours du mouvement,
l’énergie potentielle se transforme en énergie cinétique et réciproquement.
-
L’énergie mécanique
d’un système soumis uniquement à son poids reste constante.
-
Si un système est
soumis à son poids et à d’autres forces dont le travail est nul au cours du
mouvement, alors l’énergie mécanique de ce système est constante. Elle se
conserve.
|
|